线性谐振子量子特性的可视化研究
2021-10-14寇元哲郑兴荣谢凯强郑燕飞
寇元哲,郑兴荣,谢凯强,唐 歡,郑燕飞
(1. 陇东学院 机械工程学院,甘肃 庆阳 745000;2. 陇东学院 电气工程学院物理系,甘肃 庆阳 745000;3. 西南大学 物理科学与技术学院,重庆 400715)
随着量子领域的三大研究方向——量子通信、量子计算和量子精密测量的快速发展,加快发展量子科技,对促进高质量发展、保障国家安全具有非常重要的作用. 而这些方向和领域的研究基础就是基本的量子理论模型,理论研究各种量子理论模型的物理特性,如谐振子、势箱函数、氢原子的轨道和电子云图以及零点振动能等性质[1-5],其关键在于正确的模型推导和精确的仿真计算. 这些特殊的量子理论模型推导和仿真计算不但是了解物质的微观结构和宏观性质的基石,而且是所有量子理论的基础[4]. 在自然界中,任何体系在平衡位置附近的小振动都可以分解成若干彼此独立的谐振子的简谐振动,如分子的振动、晶格的振动、原子的表面振动以及辐射场的振动等. 所以说,谐振子作为量子理论体系中最典型、最基础的量子理论模型,应用于各种较复杂的体系和理论中,几十年来其理论和仿真研究一直是粒子物理、强子物理和量子通信等研究领域十分重要的课题[6-9]. 随着各学科的交叉发展,其研究在近10 年来趋于白热化[9-14]. 如:Bezák 等[8]在薛定谔方程的傅立叶分析基础上研究了线性谐振子的相关特性;张硕等[10]根据量子理论给出了球坐标系下角动量平方算符和三维谐振子哈密顿算符的本征值和本征波函数;张小伟[11]对电场中线性谐振子问题进行了求解;张迪等[12]对量子力学中线性谐振子的可视化问题进行了研究;沈曼等[13]给出了线性谐振子的坐标和动量的不确定关系;凌瑞良[14]使用不变本征算符法求解了一维线性谐振子的量子化能谱等. 这些成果虽然很好地研究了线性谐振子的各种特性,但都是独立地从理论上或者数值计算上进行了研究.
为了进一步研究n维线性谐振子的特性,本文在前期研究工作的基础上[15],重点研究了二、三维线性谐振子的本征波函数及其特性,并运用数值仿真对线性谐振子的特性做了可视化的研究. 尤其是四维图像的仿真结果对研究谐振子及其特性提供了一条便利的途径. 本文的工作弥补了前期工作的一些缺陷[15],得到了一些较好的结果,对于抽象性概念的理解具有重要意义.
1 理论模型与推导
1.1 二维线性谐振子根据空间理论,在直角坐标系下二维线性谐振子的势能函数为

由于二维谐振子的定态薛定谔方程在x和y方向上相互独立,所以基于数学物理思想,利用分离变量法,令ψ(x,y)=φ(x)φ(y),将其代入公式(2),得到二维谐振子的波函数为

这完全符合量子理论中的普朗克假设理论. 所以得到二维线性谐振子的0 点能(基态N=nx+ny=0 对应的能量)为

所以,体系中的能级简并度为


基于计算效率和仿真结果,在后面的仿真模拟中,选择自然单位ħ=μ=ω=1,则有α=1,因此归一化系数变为

1.2 三维线性谐振子同理,根据二维线性谐振子的理论模型与推导,得到三维各向同性谐振子的薛定谔方程为


在后面的模拟计算中,同样选择自然单位ħ=μ=ω=1,α=1 计算各参量.
2 结果与讨论
2.1 n 维线性谐振子的能级数值仿真根据能级的关系,运用数值仿真得到了一、二、三维线性谐振子的能级图,如图1 所示.
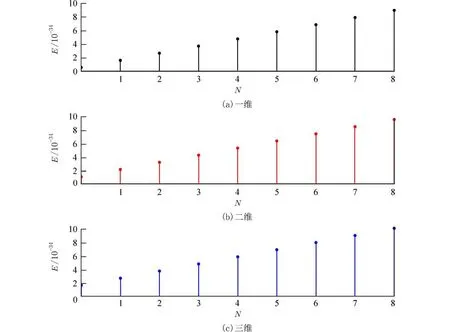
图1 一、二、三维线性谐振子能级的分布Fig. 1 The distributions of energy levels of one-,two- and three-linear harmonic oscillator
从图1 可以看出,线性谐振子能级特点:不论是一维、二维还是三维,线性谐振子能级是离散型,只能取分立值,能量是量子化的;谐振子的能级是均匀分布的,相邻两能级间隔ΔE=ħω. 这种结果符合普朗克假设,并且与理论结果完全吻合.
2.2 二维线性谐振子的数值仿真结合二维线性谐振子的理论推导,运用MATLAB 软件绘制不同能级下线性谐振子的波函数,得到了16 种情况下二维线性谐振子的波函数及其等值线图,如图2 所示. 图2 中xOy平面代表二维线性谐振子波函数的等值线.
这种波函数及其等值线图既给出了波函数的三维直观图,更能凸显出波函数的波峰、波谷. 从图2 中可以看到:二维线性谐振子的简并度为N+1,但N=0 时,对应的基态波函数无简并,如图2(a);波函数与Ψ=0 平面的交线数为N;从等值线中可以看出波峰波谷的总个数为(nx+1)(ny+1). 这种可视化的数值仿真结果与理论结果完全吻合. 同时,三维立体表示的波函数仿真图与二维平面表示的等值线图相结合的这种表示方式,既形象、直观地模拟出二维波函数的立体图形,又弥补了本文前期工作的缺陷[15].
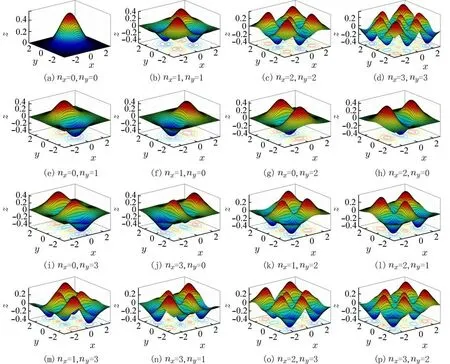
图2 16 种不同量子状态下对应的波函数及其等值线的分布Fig. 2 The distributions of the wave function and isolines at 16 diffent quantum states.
同时,结合二维谐振子的理论推导,运用MATLAB 软件绘制不同能级下线性谐振子的波函数几率密度,得到了对应的16 种情况下二维线性谐振子的波函数几率密度及其伪真彩图,如图3 所示.
从图3 可知,一般情况下,二维线性谐振子的几率密度分布的极大值个数为(nx+1)(ny+1),波函数的伪真彩图3(Ⅱ)更能直观地显示出几率密度的峰值个数与大小,其与几率密度图形成遥相呼应、互为补充的作用.

图3 16 种不同状态下的波函数几率密度及其伪真彩图的分布Fig. 3 The distributions of the wave function probability density and pseudo panel at 16 different quantum states
2.3 三维线性谐振子的数值仿真根据公式(14),结合数理方法的推导,运用MATLAB 软件的切片法,得到了三维线性谐振子的四维空间切片图,如图4 所示.
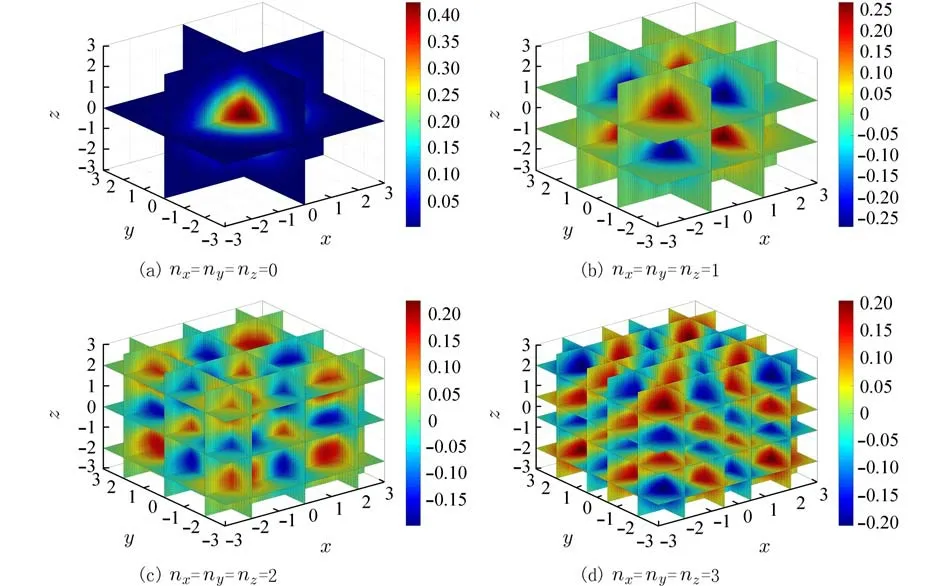
图4 不同量子状态下三维线性谐振子波函数的四维切片Fig. 4 Four-dimensional slice diagram of three-dimensional linear harmonic oscillator wave function at diffent quantum states
从图4 中可以看到:三维线性谐振子的简并度为nx+ny+nz+1;以基态波函数为准时,在一定范围内([-3,3]),x、y、z轴上的切片数分别为nx+1、ny+1、nz+1,总的切片数为nx+ny+nz+3. 截至目前,理论上对三维线性谐振子的研究很少,尤其是对三维谐振子的四维图形的研究处于空白,但本文的这种可视化结果不但与理论结果基本符合,而且弥补了四维空间图形的研究空白. 这对于抽象性概念的理解具有重要意义.
3 结论
线性谐振子作为量子理论中最重要的模型之一,其重要性不言而喻. 基于此,本文详细、全面地推导了二、三维线性谐振子的特性,如本征函数、几率密度和能级等. 同时,运用MATLAB 软件对其各项特性进行仿真模拟. 基于量子理论和数值计算,本文重点研究了量子力学中二、三维线性谐振子的基本特性,包括波函数及其能量、能级和几率密度,得到了三维和四维空间图像的可视化结果. 得到目前研究空白的三维谐振子的四维图形和二维谐振子的三维图形,弥补了本文前期工作的缺陷(二维波函数图无等高线和伪真彩图,导致波函数图形看不清楚;三维波函数图的空缺). 从理论推导和仿真图中可以得到:线性谐振子能量只能取分立值,能量是量子化的;谐振子的能级是均匀分布的,相邻两能级间隔ΔE=ħω. 二维情况下,谐振子的简并度为N+1,但N=0 时,对应的基态波函数无简并;波函数与Ψ=0 平面的交线数为N;几率密度图更能直观地显示出几率密度的峰值个数与大小,且几率密度分布的极大值个数为(nx+1)(ny+1). 三维情况下,以基态波函数为准时,在一定范围内([-3,3]),x、y、z轴上的切片数分别为nx+1、ny+1、nz+1,总的切片数为nx+ny+nz+3. 另外,本文通过MATLAB 软件首次得到了三维线性谐振子的四维空间切片图,弥补了前期工作的一些缺陷,而且填补了四维空间图像的空白. 通过这种可视化的研究,更加形象地理解了抽象的线性谐振子的一些特性,对线性谐振子有了更加深入的认识. 这种可视化的结果与理论结果完全一致,这对于抽象性概念的理解具有重要意义.
