引入滑区法的板球系统新型幂趋近律滑模控制

李江峰，向凤红

(昆明理工大学 信息工程与自动化学院，云南 昆明 650500)

板球系统作为一个典型的多变量、强耦合非线性系统，由于系统结果的直观性及模型的简易性，常用它来验证各种控制算法的性能. 针对板球系统的定点运动及轨迹跟踪问题，国内外诸多学者做了大量的研究. Ali 等[1]运用侵入性杂草优化算法优化参数，设计了板球系统的最优非线性模型参考控制器. Bang 等[2]通过提高计算效率和应用球板系统的地址来提高跟踪性能，从而在微控制器上运行，最终实现了嵌入式模型预测控制，增强了板球系统的轨迹跟踪性能. 王红睿等[3]在板球系统小球质量、半径、转动惯量未知的条件下，提出了非线性自适应控制，结合Lyapunov 稳定性理论设计了非线性自适应位置控制器，进而提高了板球系统的控制精度. 高多[4]将伺服补偿、动态输出反馈以及二次型调节等控制理论相结合，设计的控制器能够实现系统零静差跟踪，且控制器具有良好的动态品质.

滑模变结构控制其本质上是一类特殊的非线性控制，能使系统按照预定的“滑动模态”状态轨迹运动. 滑模控制具有响应快、对参数干扰不灵敏、不用系统在线识别、物理实现简单的优点，能使系统具有良好的鲁棒性和控制精度. 然而，由于开关时间和空间的滞后、系统惯性等影响会引起系统抖振，这个问题成为了滑模控制的突出障碍. 高为炳[5]以指数趋近律s˙=-εsgn(s)-κs为例，调整参数 ε 和 κ，使得系统滑动模态的到达过程具有良好的动态品质，同时控制信号的抖振幅值也得以削弱，但系统会一直抖振最终无法收敛为零. 文献[6]提出了板球系统的反步滑模自适应控制，有效地减小了系统的控制误差，但是却忽略了系统所存在的摩擦等非线性因素，具有一定的局限性. 文献[7-8]提出了扰动观测的滑模控制，能有效解决系统中存在非线性和激励不足的轨迹跟踪问题，但抖振抑制效果不够明显. 文献[9-11]为了提高系统性能，提出了级联分数阶控制器，但整体控制性能提升不显著. 文献[12]将滑模控制与监督模糊控制的方法结合起来，提高了小球球定点运动的准确性，但在轨迹跟踪控制时性能表现不佳.

为了使板球系统的滑模控制能够快速进入滑动模态阶段，本文定义了新的趋近参数，设计了用幂次函数替代符号函数的新型幂趋近律（Novel Power Reaching Law，NPRL）滑模控制器. 此控制器通过改变趋近参数调整趋近速度，同时幂次趋近律能够一定程度上抑制抖振. 但当幂趋近律的趋近参数过大使趋近速度加快的同时，系统会在滑模面产生高频振荡. 为此，本文通过在设计切换面的基础上定义了两条辅助切换面，引入了滑动区域法. 此方法能使系统在滑动区域内做低频振动，从而代替普通滑模控制在设计切换面上的高频振荡，最终系统稳定收敛到原点位置，以达到抑制并削弱抖振的目的. 设计的控制器既提高了系统响应的快速性，又削弱了快速性所引起的高频抖振问题. 通过与饱和函数替代符号函数的平滑滑模控制方案[13]、径向基函数（Radial Basis Function，RBF）网络自适应鲁棒控制方案[14]进行实验对比，验证了此控制策略的有效性.

1 板球系统的控制原理及系统模型

1.1 板球系统的控制原理选取深圳固高公司研发的GPB2001 板球系统来作为本文的实验研究平台. 板球系统的硬件结构主要由两个伺服电机、小球、球盘、连杆系统、控制器、摄像头和直流电流源组成，实物模型如图1 所示.

图1 板球系统实物模型Fig. 1 Physical model of ball and plate system

系统启动后平板上方的摄像头采集到小球的实际位置信息，控制器再将实际位置与目标位置的偏差转换成控制量，进而控制两个伺服电机拉动连接杆，连接杆带动平板运动，实现对平板倾角的控制，以完成小球在平板上定点镇定或者轨迹跟踪.

1.2 板球系统的系统建模由于板球系统是一个典型非线性系统，难以建立一个精确的数学模型，因此本文将模型进行简化和线性化处理，忽略某些因素，建模过程中作出以下假设：①不计小球与平板间的所有摩擦；②小球在平板上的所有运动均为接触式滚动；③忽略平板的倾角和角速度；④球盘无限大.

在平板上建立坐标系，选取平板的中心点处作为原点 (0,0)， 平板的x轴方向倾斜角度为 α，y轴方向的倾斜角度为 β，板球系统动力学分析如图2、3 所示[15].

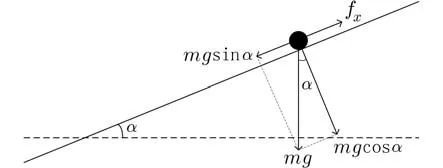
图2 板球系统的 x 轴物理模型Fig. 2 x-axis physical model of ball and plate system

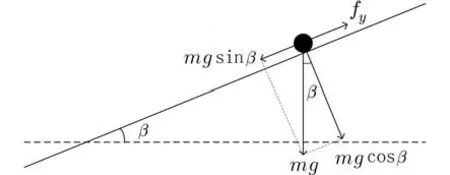
图3 板球系统的 y 轴物理模型Fig. 3 y-axis physical model of ball and plate system

本文采用拉格朗日方程建立板球系统的数学模型. 板球系统微分方程组[16]如下:

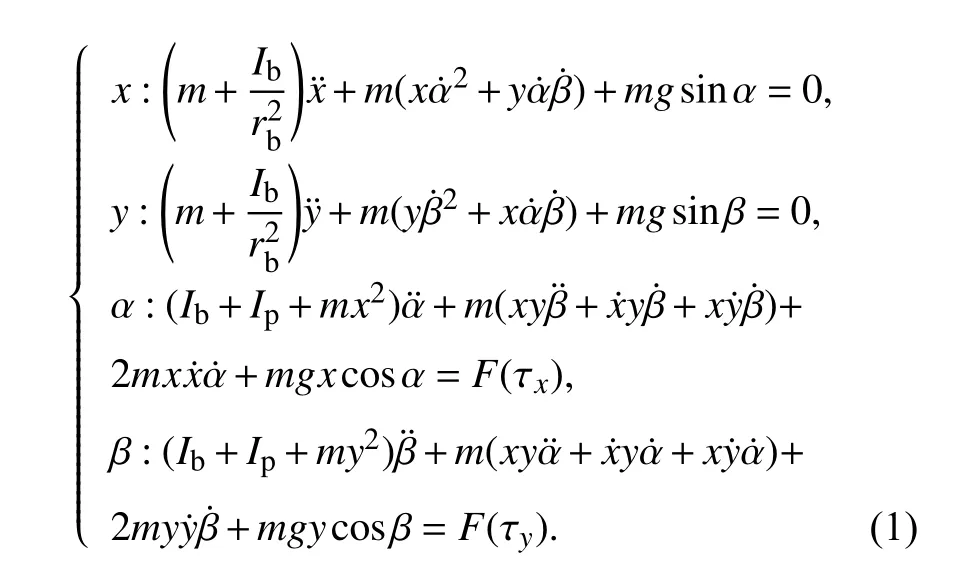
式中的各个变量参数及其意义说明如表1 所示.

表1 微分方程组中各变量意义及单位Tab. 1 The meaning and unit of variables of the system of differential equations

实际情况下，伺服电机位置固定，平板倾角只需变化很小即可控制小球，故为简化系统可以忽略平板在x、y方向的转矩，即

小球处于稳定的状态时，平板处于水平状态，此时平板倾角 α 和 β 为0，控制小球时平板的倾角变化范围也很小. 因此，倾角的正弦值可以近似为倾角本身，平板的角速度也近似为0，即

本文选取平板的倾角 α 和 β 来作为系统的输入量ux和uy，小球所对应位置坐标 (x,y) 和小球速度x˙、y˙ 分别作系统的状态x1、x2、x3和x4，最终得到系统的状态空间方程为

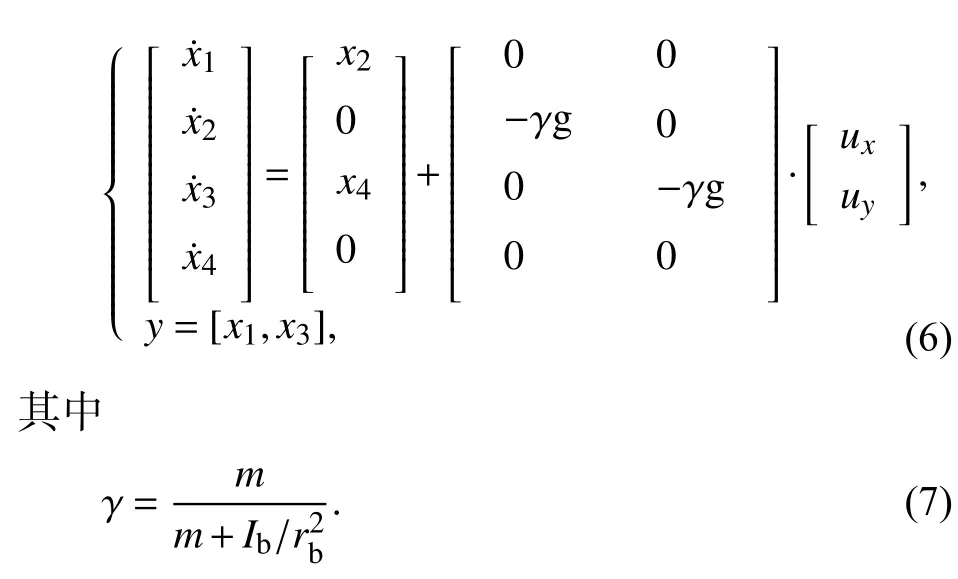
由于板球系统的两个伺服电机分别控制平板的x轴、y轴两个方向，且驱动两个方向解耦关系是相同的，故将系统分解成分别关于x轴和y轴的两个子系统，对两个子系统分别设计控制器. 关于x轴和y轴的两个子系统有着相同的模型，故在本文设计分析x轴的子系统同样也能在y轴子系统实现.

2 引入滑动区域法的新型幂趋近滑模控制器设计

滑模控制是一种特殊的非线性控制，它的系统结构会随时间变化，其突出特点就是在满足一定的条件下系统能沿预定轨迹运动. 滑模控制具有良好的动态性能，在实际工程中运用较为广泛，因此也受到了国内外学者的重视. 但是滑模控制存在着无法完全消除抖振的问题，为了加快系统响应速度且解决滑模控制板球系统在切换面附近存在的高频振动问题，设计了引入滑动区域法的新型幂次趋近律滑模控制器.

2.1 板球系统的滑模控制器设计滑模控制系统运动过程分为趋近运动过程和滑动模态两个阶段，故可将滑模控制律ut(x,t) （ 文中简记为ut）分为切换控制un(x,t)（ 文中简记为un） 和等效控制ueq(x,t)（文中简记为ueq）.

板球系统x轴子系统为二阶非线性单输入单输出系统，且在建模时忽略了摩擦以及不确定性时变干扰等因素，故引入不确定项kx(t)，则有

2.2 引入滑动区域法的滑模等效控制在原设计切换面的基础上引入辅助切换面概念，由辅助切换面所围成的区域定义为滑动区域. 以二维状态空间为例，由误差及误差率构成的相平面如图4 所示[17]. 其中，s为原设计切换面，s1、s2为辅助切换面，且

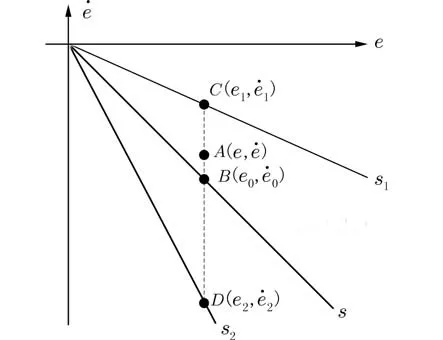
图4 滑动区域二维模型Fig. 4 Two-dimensional model of sliding region

其中，a1和a2为大于零的参数.

当系统结束了趋近阶段进入到滑动区域后，系统的等效控制将由辅助切换面及设计切换面同时发挥作用，以达到削弱高频抖振的目的，使得控制系统得到优化. 同时，必须满足趋近运动阶段与滑动模态之间是连续的，并且当系统处于设计切换面时，辅助切换面不起作用.

当系统进入滑动区域并处于s1与s之间的点A(e,e˙) 时，过A作 垂 直e轴 的 直 线 与s1相 交 于C(e1,e˙1)， 与s相交于B(e0,e˙0). 同理，当系统位于s与s2之间时则有D(e2,e˙2).

此时等效控制为

本文控制器输出的目的是为了让系统在滑动模态阶段既不单纯地在设计切换面上运动，也不在辅助切换面上运动，从而避免了滑模控制带来的抖振. 通过设计切换面和辅助切换面对系统运动点的控制差调整板球系统的滑模控制器. 当运动点距离s较近点时，式（15）的分子增大分母减小，式（14）由s求得的控制量在总的控制量中占比较少，从而避免了系统在设计切换面附近可能会产生的系统状态抖振. 当运动点距离s1较近时，式（15）的分子减小分母增大，式（14）由s所求得的控制量在总的控制量中占比多，又将系统拉离s1，使系统始终在滑动区域内且不长时间停留在设计切换面上运动.当系统运动到s与s2之间时，原理同上. 随着s1与s2最终收敛到相平面原点，运动点也将在滑动区域内逐步收敛. 通过调整i值的大小优化控制器的控制输出品质.

2.3 新型幂趋近律当系统在未进入滑区时，只考虑设计切换面s的存在，辅助切换面s1和s2不起作用，此时控制器与普通滑模控制器相同，直到系统进入滑动区域为止. 此过程为趋近运动.

因符号开关函数的存在，滑模控制不可避免地会在切换面附近产生抖振，但变结构是由开关函数所定义的，去除开关函数系统会失去鲁棒性[18]. 此外，趋近参数（切换增益）也是引起抖振的重要原因. 因此本文设计了新的趋近参数，同时用幂次函数代替符号开关函数的NPRL 方案.

相较于传统的符号函数和饱和函数，新型幂次函数的趋近参数具有较好的自适应调节效果. 当s较大（远离切换面）时趋近参数也增大，从而有更快的趋近速度；s较小（靠近切换面）时趋近速度也相应减小；当s为0（到达切换面）时，趋近速度为0，保证了切换增益随着运动点变化而变化，以达到加快趋近速度且降低抖振的效果. 同时，在穿越切换面时幂次函数的开关函数过渡曲线连续光滑，可有效降低滑模控制中的抖振. 新型幂次函数、符号函数和饱和函数如图5 所示.

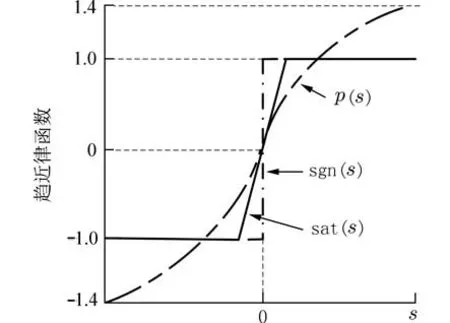
图5 开关函数Fig. 5 Switching function

新型幂趋近律表达式为

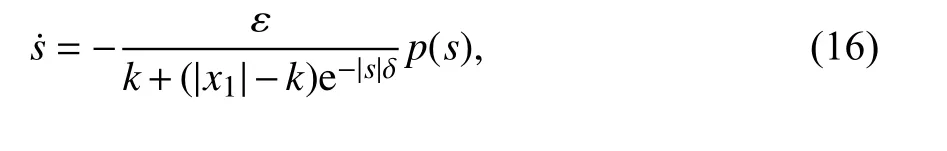
2.4 稳定性分析当系统未到达滑动区域而处于趋近模态的过程中，为了保证系统能够进入到滑动区域并且保持系统稳定，建立了Lyapunov 函数

显然（20）及（21）式均负定，因此系统渐进稳定. 系统将存在s0、s1和s23 个平衡点，当系统进入到滑动区域后将最终收敛于原点. 当系统位于辅助切换面上时，因设计切换面控制输出起主要作用，会将系统拉到设计切换面附近，但由式（14）可知，系统位于设计切换面上时，辅助切换面却不发挥作用，但实际的滑模控制器不会让系统始终位于设计切换面上，因此系统会在滑动区域内做低频的振荡，以达到减弱抖振的效果.

3 仿真结果和分析

为了验证在NPRL 基础上引入滑动区域的板球系统滑模控制的轨迹跟踪精度和动态性能，设计了板球系统的轨迹跟踪模型，通过与饱和函数替换符号函数的平滑滑模控制、RBF 网络自适应鲁棒滑模控制器进行仿真对比，分别对系统进行了轨迹跟踪及误差跟踪，同时对控制输出也进行了仿真对比. 跟踪的预设曲线为心形曲线，表达式如（22）式，参数变量取值如表2，单位参照表1.

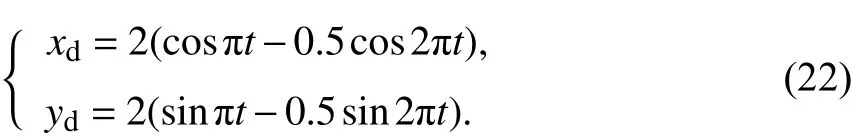
表2 变量参数值Tab. 2 Parameter values of variables

为了验证受到外界干扰下设计控制器的性能，引入了干扰函数如下所示：

经仿真实验对比，3 种控制器输出如图6～8所示. 由此可得，仅用饱和函数替换符号开关函数的平滑滑模控制器输出产生了高频、幅值为1.5 左右的振荡，且振荡一直持续，易引起模型的摄动；RBF 网络自适应鲁棒滑模控制器输出具有较低的抖振频率，但平稳后振荡的幅值在-2～1，且开始输出具有-3.5～5.9 的高幅突变；引入滑动区域法的NPRL 控制器输出仅在开始有轻微的抖振，随后能保持低频低幅值抖振稳定输出，说明所设计控制器对系统的动态性能与稳态精度均有保证.

图6 平滑滑模控制器输出Fig. 6 Output of smooth sliding mode controller

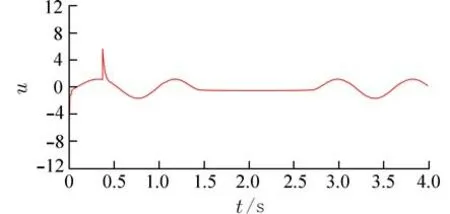
图7 RBF 网络自适应鲁棒控制器输出Fig. 7 Output of adaptive robust controller based on RBF network

图8 滑动区域法新型幂趋近律控制器输出Fig. 8 Output of novel power reaching law controller based on sliding region method

图9～12 分别为板球系统的轨迹跟踪及误差跟踪对比. 在同等的输入条件下本文方案控制的小球在0.176 s 左右就能跟踪到预定轨迹，而使用平滑滑模控制在0.330 s 左右跟踪到预定轨迹，RBF网络自适应鲁棒控制的轨迹跟踪用了0.450 s，通过轨迹跟踪对比显示出所设计控制器的快速性.

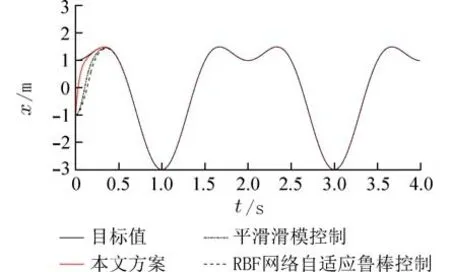
图9 x 轴轨迹跟踪曲线对比Fig. 9 Comparison of x-axis trajectory tracking curves

图10 y 轴轨迹跟踪曲线对比Fig. 10 Comparison of y-axis trajectory tracking curves

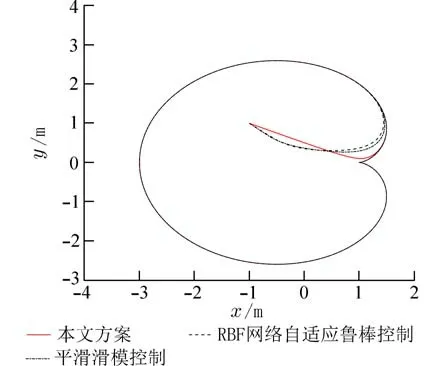
图11 板球系统轨迹跟踪曲线对比Fig. 11 Comparison of trajectory tracking curves of ball and plate system

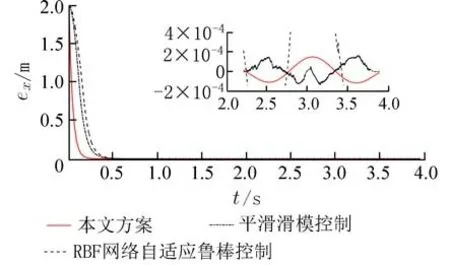
图12 x 轴误差跟踪对比Fig. 12 Comparison of x-axis error tracking

由图12，本文设计的控制器使小球跟踪误差快速衰减. 当系统稳定输出后，误差在(-0.46 ～0.23)×10-4m 时，误差曲线较为平滑；平滑滑模控制小球的误差在 ( -0.25 ～0.91)×10-4m 时，误差曲线存在高频的振荡；RBF 网络自适应鲁棒控制小球的误差值较大，在零误差线上下进行高幅值的来回波动.

通过控制器仿真对比可得，定义的新型趋近参数能够使系统具有较好的动态性能，幂趋近律及滑动区域法同时作用削弱了系统产生的高频抖振，提高了系统的稳态精度，从而验证了设计控制器的有效性.

4 结论

本文设计控制器的控制对象为板球系统，主要是定义了新的趋近参数，同时用幂次函数代替符号函数，在此基础上引入了滑动区域的滑模控制方法. 此控制器旨在利用新定义的趋近参数来加快系统响应的速度，且能在系统到达切面时具有较小的切换增益；同时，运用幂次函数替代符号函数，削弱符号开关函数引起的抖振；在此基础上引入了滑动区域，让运动点受辅助切换面和设计切换面共同作用，进一步削弱系统的抖振. 通过仿真对比分析验证了方法的可行性及输出的稳定性. 结果表明，相比于饱和函数代替符号函数的平滑滑模控制器及RBF 自适应鲁棒控制器，本文所设计的控制器加快了板球系统的跟踪速度，提高了系统的动态品质及稳态精度，还能有效地削弱系统所产生的抖振，证明了控制策略的有效性. 下一步的工作是针对x、y轴之间的耦合问题开展进一步的研究.