A Novel Parameter-Free Filled Function and Its Application in Least Square Method
2021-10-14
(1.School of Mathematics and Statistics, Henan University of Science and Technology, Luoyang 471000, China; 2.Business School, University of Shanghai for Science and Technology, Shanghai 200093, China)
Abstract: The filled function algorithm is an important method to solve global optimization problems.In this paper, a parameter-free filled function is proposed for solving general global optimization problem, discuss the theoretical properties of this function and give the corresponding algorithm.The numerical experiments on some typical test problems using the algorithm and the numerical results show that the algorithm is effective.Applying the filled function method to the parameter solving problem in the logical population growth model, and then can be effectively applied to Chinese population prediction.The experimental results show that the algorithm has good practicability in practical application.
Keywords: Global optimization; Parameter-free filled function; Logistic population growth model; Chinese population prediction
§1.Introduction
Global optimization is more and more widely used in practice, such as molecular biology,neural network, environmental engineering, etc.It is usually used to solve the abstract global optimization problem and make optimal design and decision, and has been extended to many important fields, such as economy, science, national defense and so on.The global optimization algorithm is the key step in solving the global optimization problem.Especially, with the coming of the era of big data, this puts forward higher requirements for global optimization theory and algorithm.There are many ways to solve global optimization problems, including stochastic methods and deterministic methods.The filled function method is a deterministic method that can effectively solve general global optimization problems without specific structures.
The filled function algorithm is to construct a filled function and use the filled function to jump out of the neighborhood of the current local minimum point, so as to find a better local minimum point.It consists of two phases: local minimization phase and filling phase.In the minimization phase, a local minimization algorithm is used to obtain a local minimizer of the original problem.In the filling phase, the original problem is minimized by means of the filled function, and the two phases are alternated until a global minimizer is found.
As one of the effective methods to solve global optimization problems, it was first proposed by Ge [3], and a filled function with an exponential term and two adjustable parameters was given.However, such a filled function with an exponential term may lose the optimal solution of the original problem or find a false stationary point.To solve this problem, Ge and Qin [4]proposed seven new filled functions, but some of them were still affected by exponential terms.Subsequently, Liu [7]proposed a new single-parameter filled function, which did not contain exponential terms and avoided the above problems.In order to construct a good filled function,professor Zhang [17]improved the definition of filled function in 2004 and led the team to proposed a series of filled functions with better performance.For example, for nonlinear integer programming, Shang et al.[12]proposed a single parameter filled function; For unconstrained global optimization, professor Yang et al.[11,16]proposed new methods of filled functions;For constrained global optimization problem, professor Wang et al.[14]proposed a single parameter filled function.Since then, scholars have proposed many different forms of filled functions [1,5,6,9,10,13,15,18].
Through the analysis, we find that the improper selection of parameters may lead to the failure of the filled function method or the difficulty of numerical calculation.To break the limitations, in this paper, a new parameter-free filled function without exponential terms is proposed.The paper is organized as follows.In the Sect 2, a new filled function without any parameters is proposed and its theoretical properties are investigated.In the Sect 3, new filled function algorithm is presented.In the Sect 4, four numerical examples are given, and both theoretical analysis and numerical experiments show that the proposed algorithm based on this filled function can obtain higher computational global optimal solutions with a relatively few number of iterations.In the Sect 5, the algorithm is applied to the Logistic population growth model.Through calculation, the algorithm also has a good adaptability in practical application.
§2.A new filled function and its properties
The following global optimization problem will be discussed
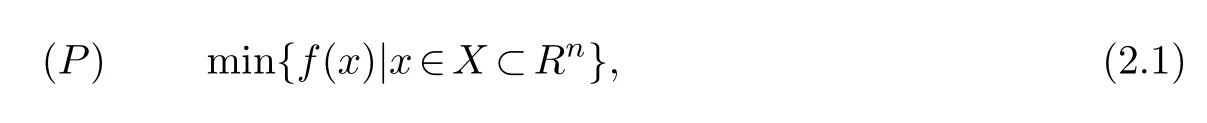
wheref:Rn →R and X={x∈Rn|ai ≤xi ≤bi, i=1,2,···,n}.
Throughout this paper, we assume that the following conditions are satisfied.
Assumption 2.1.f(x)is a coercive function, that is f(x)→+∞, as ‖x‖→+∞.
Notice that Assumption 2.1 implies that there exists a bounded and closed set Ω⊂Rnwhose interior contains all minimizers off(x).It can ensure that the value off(x) forxon the boundary of Ω is greater than the value off(x) for anyxinside Ω.Then the original problem(P) is equivalent to the following problem:

Assumption 2.2.The set F={f(x*)|x*∈L(P)} is finite, where L(P)is the set of all minimizers of problem(P)*.
Note that Assumption 2.2 only requires that the number of local minimal values of problem(P)*be finite.The number of local minimizers can be infinite.



Theorems 2.5 and Theorems 2.6 ensure that whenxgoes away fromx*k, the filled function value decreases and obtain points in the region Ω2wheref(x)<f(x*k).
Theorems 2.1-2.6 guarantee that if the current minimizer is not a global one, the filled function has a minimizer at which the objective function value is lower than the current minimum value of the objective function.An optimization algorithm will be described in the next section,it employs the presented filled function.
§3.Filled function algorithm
Based on the above theorems and discussions, we describe a global optimization algorithm for solving problems (2.2).The algorithm steps are as follows:


§4.Numerical experiment
In this section, we implement numerical tests for four examples.All these tests are programmed in a computer with an Intel(R) Core(TM)i5-7500CPU@3.40GHz8G in Matlab R2016a.
The main iterative results are summarized in tables for each function.The symbols used are the following:
k: The iteration number in finding the k-th local minimizer.
: The starting point in the k-th iteration in finding the k-th local minimizer.
: The k-th local minimizer.
f(): The function value of the k-th local minimizer.
iter: Number of iteration steps of the algorithm.Pro.1: Two-dimensional Restrign function:
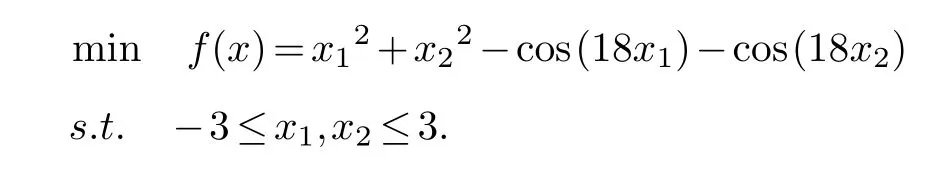
Its global minimizer isx*=(0,0),f(x*)=-2.
The proposed filled function approach succeeds in identifying a global minimum solution(see Tab 1).
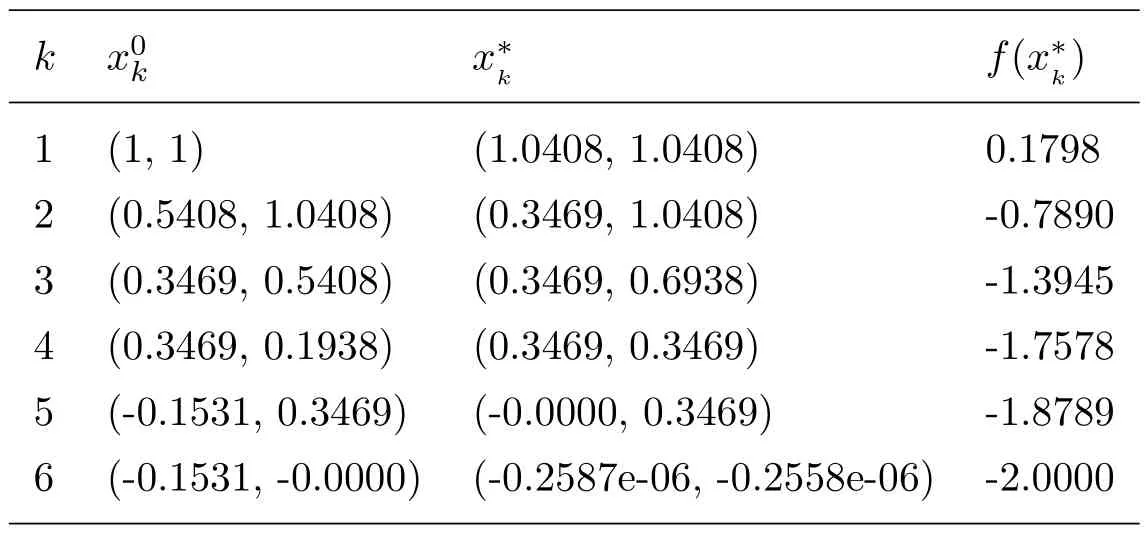
Table 1 Numerical results of Pro.1
Pro.2: Two-demensional function:
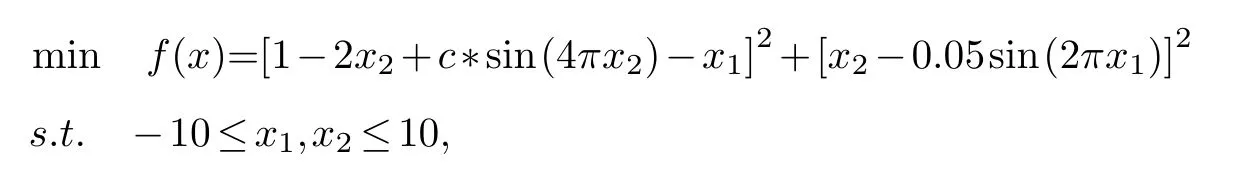
wherec=0.05.
The global minimum value isf(x*)=0.
The proposed filled function approach succeeds in identifying a global minimum solution(see Tab 2).
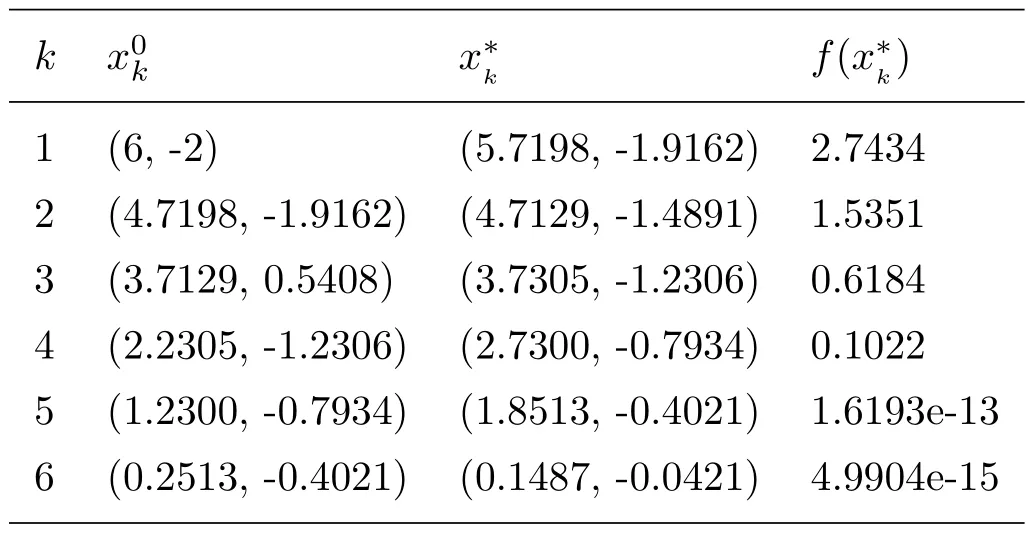
Table 2 Numerical results of Pro.2
Pro.3: Two-dimensional Shubert function:
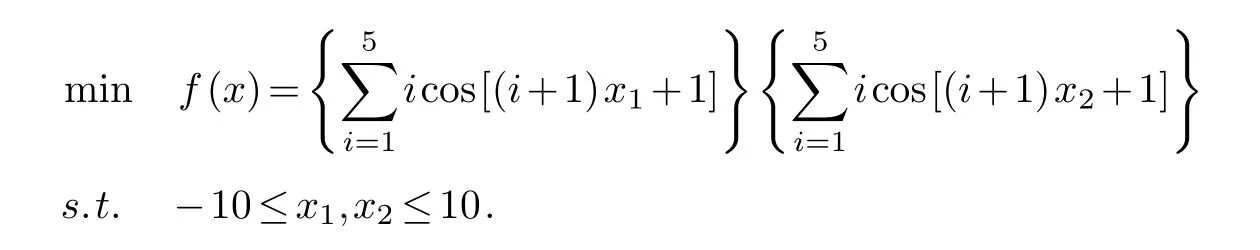
The global minimum value isf(x*)=-186.7309.
The proposed filled function approach succeeds in identifying a global minimum solution.(see Tab 3)
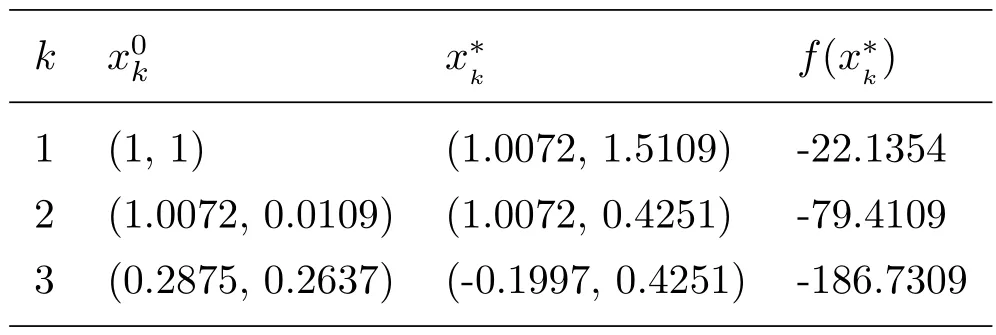
Table 3 Numerical results of Pro.3
Pro.4: N-dimensional Sine-square function:
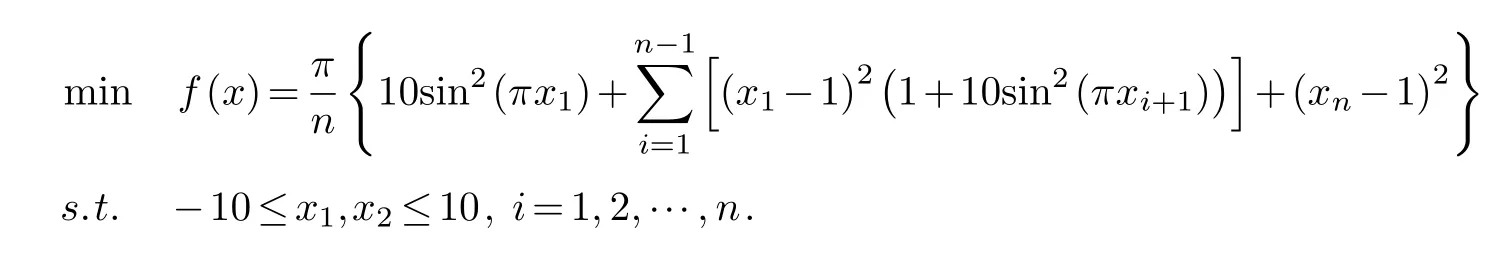
The function is tested forn=3, the global minimum solution is uniformly expressed asx*=(1.0000,1.0000,1.0000) andf(x*)=0.
The proposed filled function approach succeeds in identifying a global minimum solution(see Tab 4).
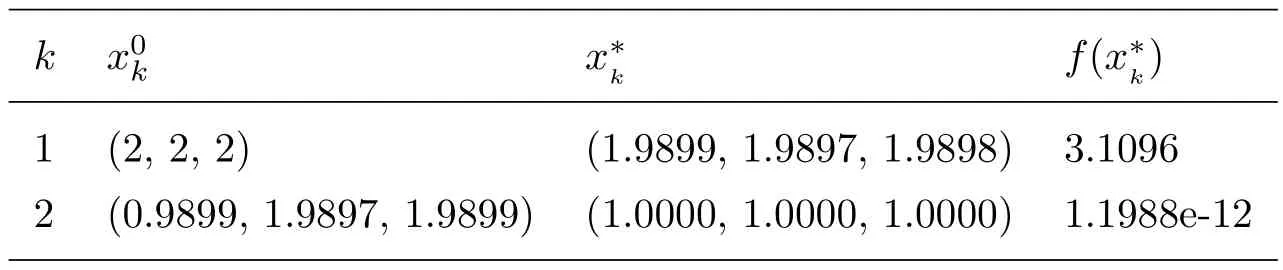
Table 4 Numerical results of Pro.4
The numerical results in this paper were compared with those in [1](see Tab 5).
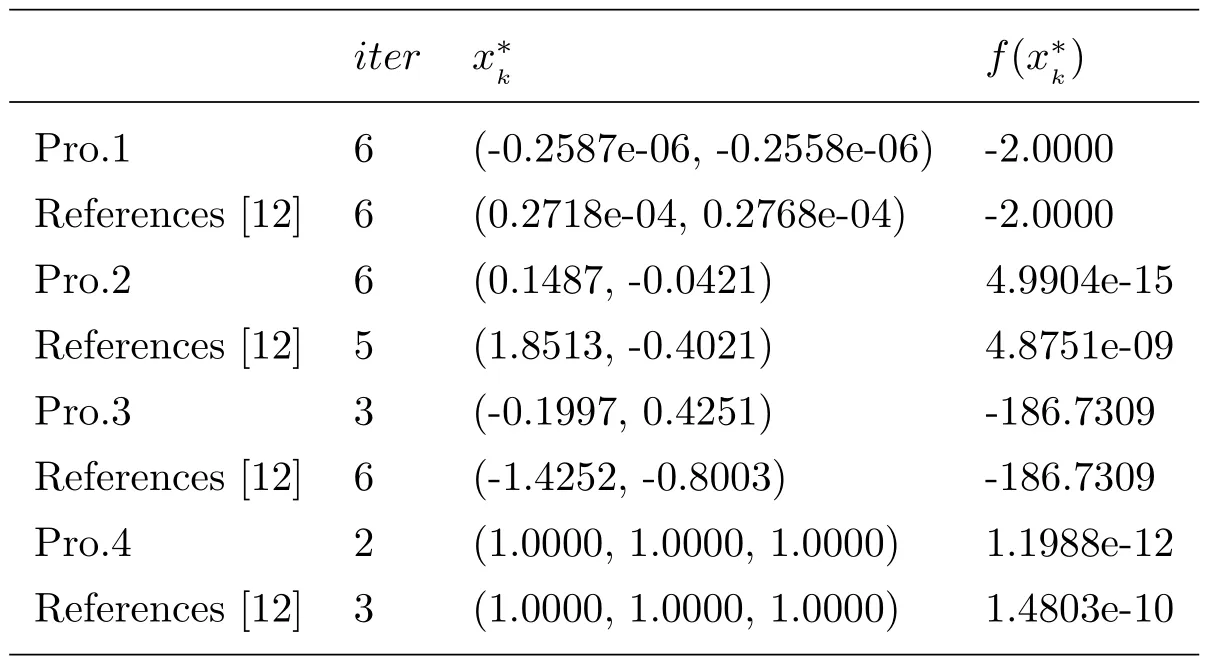
Table 5 Compared with paper [12]
Numerical results show that the global optimal solution and optimal value of the above four examples can be obtained by the filled function algorithm constructed in this paper,and compared with examples in [1].The results of Example 1 and Example 2 show that our calculation accuracy is higher.The results of Example 3 and Example 4 show that the algorithm based on this filled function only needs a relatively small number of iterations and can find the optimal solution with higher accuracy.
§5.The application of filled function in data experiment
5.1.Background and questions
To study the variation of population and species (fish stocks in fish ponds, plants in deep forests, etc.), embedding mathematical models and improving them, can be used to predict changes in population and species.Common mathematical models include exponential growth model and block growth model (Logistic growth model [2]).
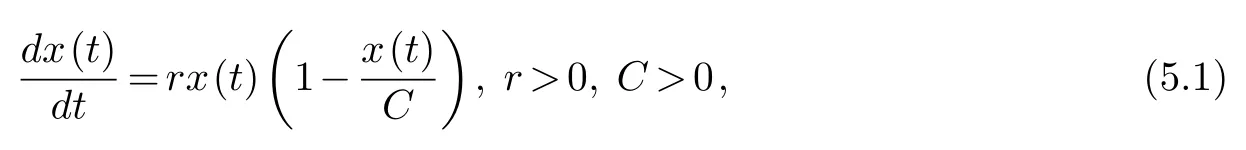
Logistic growth model:wherex(t) represents the number of the population at timet, rrepresents the natural growth rate of the population (i.e., birth rate minus death rate), andCrepresents the environmental carrying capacity (i.e., the maximum number of the population that can be accommodated by the environment).
5.2.Improvement and solution of the model
With the deepening of the research, we believe that the growth rate of the population will also change with the change of the natural environment.In order to better reflect the change status of the population in the complex environment, the growth raterneeds to be expressed as a functionr(t) of timet, and the harvest functionH(t) should be related to the growth rater(t).Suppose there is a linear relationship between the harvest functionH(t) and the growth rater(t), there is a constantkthat makesH(t)=kr(t), then an improved Logistic growth model is obtained:
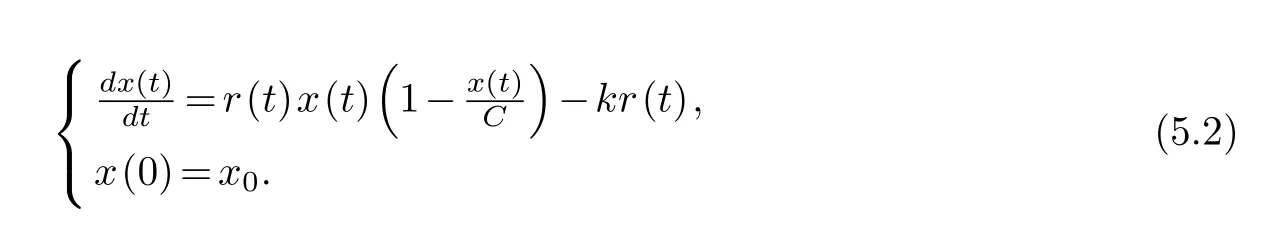
The exact solution of equation (5.2) can be obtained through variable separation and sorting:
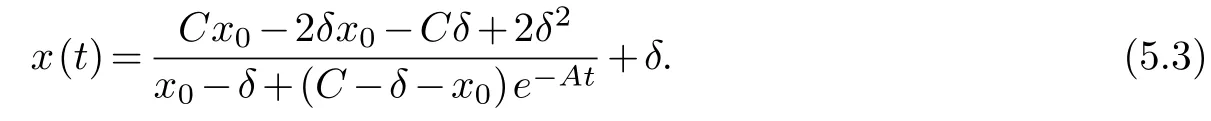
The accuracy of parameter estimation in the model directly affects the accuracy of population prediction.
5.3.Analysis and hypothesis
The predicted population at timetis denoted asx(t), andxtis the actual population at timet, the relationship between the two is denoted asf(C,δ,A),Qrepresents the residual difference between the observed value and the actual value,Qsmaller, the better the prediction.The principle of least square method is used to estimate the unknown parametersC,δ,A.
In this paper, the problem of solving parametersC,δ,Ais transformed into the following unconstrained problem:
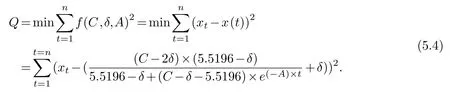
For the convenience of expression, parameters in Equation (5.4) are processed to makeα1=C, α2=δ, α3=A.According to the official website of the National Bureau of Statistics,refer to China’s population data for 1950-2018 in [2].The filled function algorithm is used to find more ideal parameters.
Give the initialα0=(18.0571,3.4708,0.0603) of parameter estimation, the filled function algorithm is used to obtainα0=(18.2712,3.6699,0.0622) after two iterations.The residual difference between the predicted value and the actual value is 0.5219.The Lsqcurvefit function was used to estimate the parameter=(18.2746,3.6727,0.0623) in [2].The residual difference between the predicted value and the actual value is 0.5226.To sum up, the filled function algorithm can achieve the same effect as Lsqcurvefit function in the problem of inverse parameter of Logistic growth model or even better.
So takeC=18.2712,δ=3.6699,A=0.0622.Therefore, the optimal estimation results are substituted into the model:
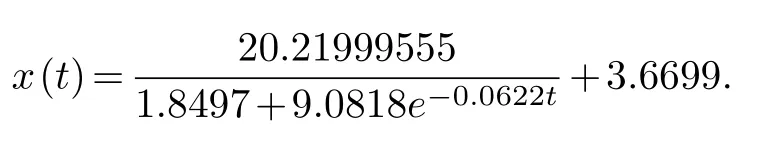
§6.Conclusion
In this paper, a new filled function without parameters is constructed.Based on the constructed filled function, a new filled function algorithm is designed.Compared with the numerical results in [1], the effectiveness of the algorithm is verified.At the same time, applying the filled function method to the parameter solving problem in the logical population growth model.The experimental results show that the algorithm has good adaptability in practical application.
杂志排行
Chinese Quarterly Journal of Mathematics的其它文章
- Batalin-Vilkovisky Structure on Hochschild Cohomology of Self-Injective Quadratic Monomial Algebras
- Continuous Dependence for a Brinkman-Forchheimer Type Model with Temperature-Dependent Solubility
- Continuous Dependence for the 3D Primitive Equations of Large Scale Ocean Under Random Force
- Y-Gorenstein Cotorsion Modules
- Sparse Reduced-Rank Regression with Outlier Detection
- The Optimal Matching Parameter of Half Discrete Hilbert Type Multiple Integral Inequalities with Non-Homogeneous Kernels and Applications
