Continuous Dependence for a Brinkman-Forchheimer Type Model with Temperature-Dependent Solubility

(1.School of Date Science, Guangzhou Huashang College, Guangzhou 511300, China; 2.Foundation Department, Guangdong AIB University, Guangzhou 510507, China)

Abstract: The structural stability for the Brinkman-Forchheimer equations with temperature-dependent solubility in a bounded region in R3 was studied.The reaction boundary conditions for the temperature T and the salt concentration were imposed.With the aid of some useful a priori bounds, we were able to demonstrate the continuous dependence result for the Forchheimer coefficient λ.

Keywords: Structural stability; Brinkman-Forchheimer equations; Temperaturedependent solubility; Continuous dependence; Robin boundary

§1.Introduction

There has been substantial recent interest in deriving stability estimates where changes in coefficient are allowed.This type of stability has earned the name structural stability.This means changes in coefficients in the partial differential equations may be reflected physically by changes in constitutive parameters.We believe that the mathematical analysis of these equations will help to reveal the applicability of them in physics.On the other hand, continuous dependence results are important because of the inevitable error that arises in both numerical computation and the physical measurement of data.It is relevant to know the magnitude of the effect of such errors on the solutions.The fluid flows in porous media have been widely studied.Most of them focus on the Brinkman, Darcy and Forchheimer models.Many references to the work of the nature are given in the monograph of Ames and Straughan [2].These model equations in a porous medium were discussed in the books of Nield and Beijan [19]and Straughan [32,33].Several papers in the literature have dealt with Saint-Venant type spatial decay results for Brinkman, Darcy, Forchheimer and other equations for porous media, see,for example [20–22,28,31].The work on stability and continuous dependence questions in porous media problems has been carried out by Ames and Payne [1], Franchi and Straughan [7],Payne and Straughan [23–25], Payne, Song and Straughan [27], Lin and Payne [3–6,8–18,29,30].Recently,some new results were obtained by many papers(see[3,4,7–13,15–18,23–25,27,29,30]).

In[5],Chen and Liu investigated the structural stability for Brinkman-Forchheimer equations with temperature-dependent solubility in a bounded region in R3:

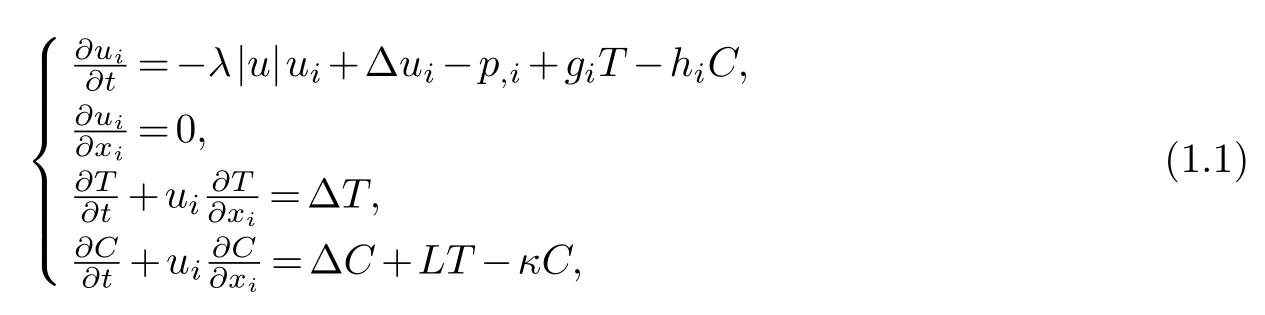
whereui,p,TandCare velocity, the pressure, the temperature and the salt concentration.λis the Forchheimer coefficient.Lis the chemical equilibrium coefficient andκis the salt concentration coefficient.Heregi(x)andhi(x)are gravity vector functions, we assumegisatisfy|g|≤G1and|∇g|≤G2,hisatisfy|h|≤H1and|∇h|≤H2.△is the Laplacian operator.The model equations (1.1) were based on the equations of balance of momentum, balance of mass,conservation of energy, and conservation of salt concentration.They adopted a Forchheimer approximation in the body force term in the momentum equation (see [6,32]).In [5], the structural stability for the Brinkman-Forchheimer equations (1.1) were studied.They obtained both the continuous dependence and the convergence results for the Forchheimer coefficientλunder homogeneous Neumann boundary for temperatureTand the salt concentrationC.In the present paper, we continue the work of [5], and we consider the continuous dependence for the Forchheimer coefficientλunder reaction boundary conditions for the temperatureTand the salt concentrationCwhich have been used in [29].These boundary conditions indicate that the values of the outer normal vectors of Temperature and salt concentration are dependent on the salt concentration.In this case, we can’t obtain the maximum principle forTandCas in [5].We must seek new method to estimates the convection termWhat’s more, the boundary conditions forTandCare difficult to tackle.We have never seen any papers dealing with the structural stability of equations (1.1) under these boundary conditions.We think our result is new and interesting.

Equations (1.1) hold in the region Ω×[0,τ], where Ω is a bounded, simply connected and strongly star-shaped domain with boundary∂Ω inR3, andτis a given number satisfying 0≤τ ＜∞.The boundary and initial conditions are given by

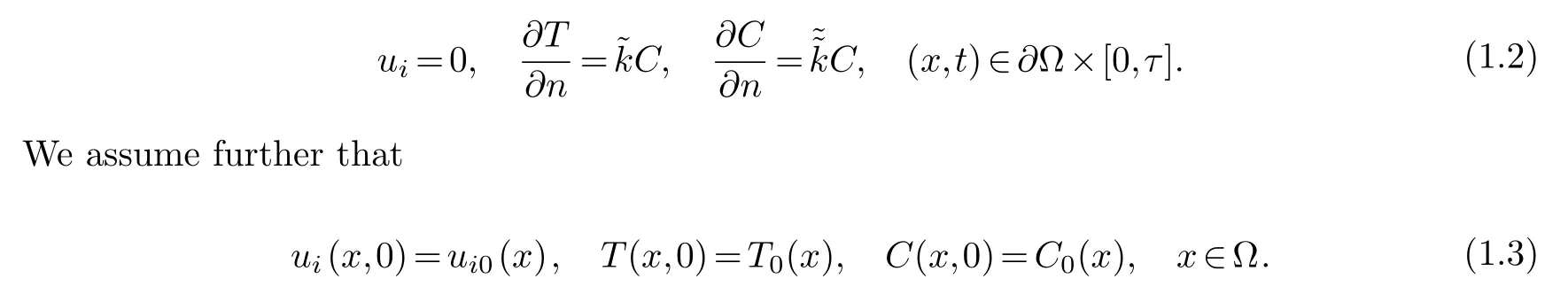
In the present paper, the comma is used to indicate differentiation, the differentiation with respect to the directionxkis denoted as, k, and the differentiation with respect totis denoted as,t.Thusu,idenotesandu,tdenotesThe usual summation convection is used in this paper.The repeated Latin subscripts is used to sum from 1 to 3.Hence,

§2.Bounds for the temperature T and the salt concentration C

In this part,we will get some useful bounds for the temperatureTand the salt concentrationCin proving our main result.

Multiplying (1.1)3by 2Tand integrating over Ω×[0,t], we find

§3.Continuous dependence for the Forchheimer coefficient λ

Inequality (3.28) establishes Theorem 1 which demonstrates continuous dependence onλin the indicated measure.