Continuous Dependence for the 3D Primitive Equations of Large Scale Ocean Under Random Force

( Department of Apllied Mathematics, Guangzhou Huashang College, Guangzhou 511300, China)

Abstract: In this paper,we consider the initial-boundary value problem for the large scale three-dimensional (3D) viscous primitive equations under random force.Assuming that the random force and the heat source satisfy the some assumptions, we firstly establish rigorous a priori bounds with coefficients which depend only on boundary data, initial data and the geometry of the problem, and then with the aid of these a priori bounds,the continuous dependence of the solution on changes in the heat source is obtained.

Keywords: Primitive equations of the ocean; The heat source; Continuous dependence;Random force

§1.Introduction

In the past many years, a lot of research works about the well-posedness of the above 3D deterministic primitive equations of the large-scale ocean have been appeared in the literature.One can refer to Huang and Guo [3,17], Hieber et al [16], Guo et al [12,14], You and Li [34],Jiu et al [18], Chiodaroli and Mich´elek [7], Sun et al [32,33], Cao et al [4,5], Chiodaroli and Mich´alek [9], Zheng and Wang [35], Dong, Zhai and Zhang [8].In study of the primitive equations of the large-scale ocean or atmosphere, it is very reasonable and necessary to consider the stochastic external factors in the model.One reason of considering such fast oscillating random force in the primitive equation is that white noise is an idealistic model.For a more detailed introduction and application of the model, one can see [1,2,6,20,25,29].Under some assumptions on the random force, Guo et al [14]obtained the diffusion limit and the global well-posedness to 3D primitive equations of the large-scale ocean under fast oscillating random force.

Different from the results above, in this paper we consider the continuous dependence for the 3D primitive equations with fast oscillating random force which always exits in realistic model.It is very important to know whether a small change in the equation can cause a large change in the solution.While we take advantage of the mathematical analysis to study these equations, it is helpful for us to know their applicability in physics.Since there will appear some inevitable errors in reality, the study of continuous dependence or convergence results becomes more and more significant.In the past several years, there have been many papers in literature to study the continuous dependence for varieties of equations (e.g., Brinkman, Darcy and Forchheimer equations) (see [15,21,23,26–28,30,31]).But as far as we know, there are few articles concerning the continuous dependence of solutions of the 3D viscous primitive equations in a cylinder which is very necessary to study in practice.Since the model we are studying is highly nonlinear, the analysis, as shown here, is non trivial.It is worth stressing that the ideas developed in this paper are helpful to study the other type primitive equations with other kinds of boundary conditions.

In this paper, we use that the symbol Ω designates the subdomain of R3for

whereMis a smooth bounded domain in R2.We note the boundary of Ω as

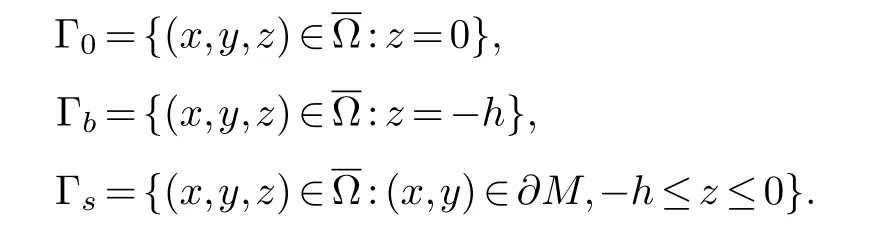
The 3D primitive equations in Ω we consider in this paper are (see [13,14])

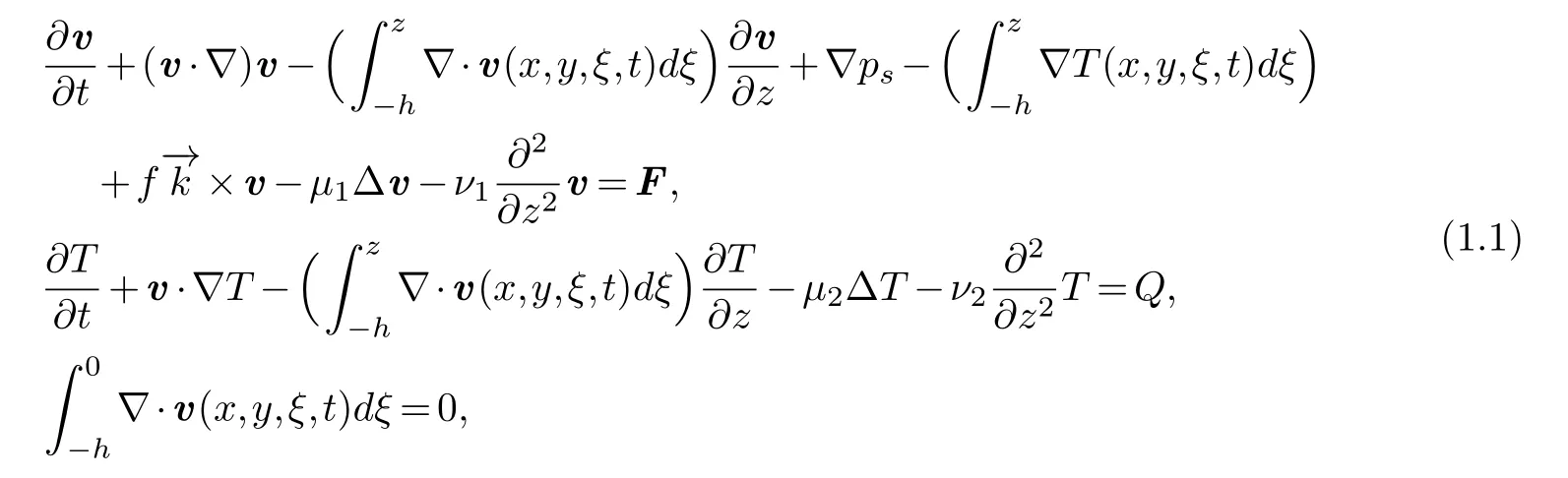
where the horizontal gradient operator∇=(∂x,∂y), the horizontal velocity fieldv=(v1,v2), the temperatureTand the pressurepare the unknowns.f=f0(β+y) is the Coriolis parameter,is the vertical unit vector,is the given forcing field, whereWis a Wiener process on two sides of time.Qis the given heat source.are positive constants representing the horizontal and vertical Reynolds numbers, respectively, andν1,ν2are positive constants which stand for the horizontal and vertical heat diffusion, respectively.Without loss generality, we supposeμ1=μ2=ν1=ν2=1.

The system (1.1) also has the following boundary conditions (see [6])

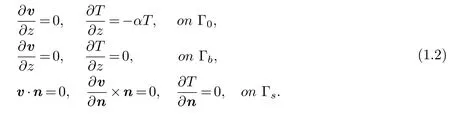
The boundary conditions show that the wind stress is zero and the heat dissipation rate is a linear function ofTon the surface of the ocean.There is no exchange between the fluid and the outside in the rest of the cylinder boundary.

In addition, the initial condition can be written as

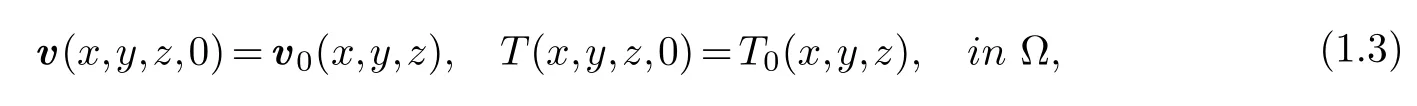
wherev0(x,y,z), T0(x,y,z) are nonnegative continuous functions.

The plan of the paper is as follows.In next section we give the main result of the problem and some well-known inequalities which will be used in the whole paper.Inspired by [3,35], we establish rigorous a priori bounds with coefficients in section 3.Finally, we give the proof of our main result in section 4.

§2.Main result

To get our main result, we give some preliminaries.Supposingbe an another solutions of (1.1)-(1.3) with different given forcing fieldF*and given heat sourceQ*.Let

§3.A priori bounds

Lemma 3.1.If T0,Q∈L∞(Ω), then the solution T of(1.1)3satisfiessupΩ|T|≤Tm, where Tm= supΩ{||Q||∞, ||T0||∞}.

§4.The proof of Theorem 2.1

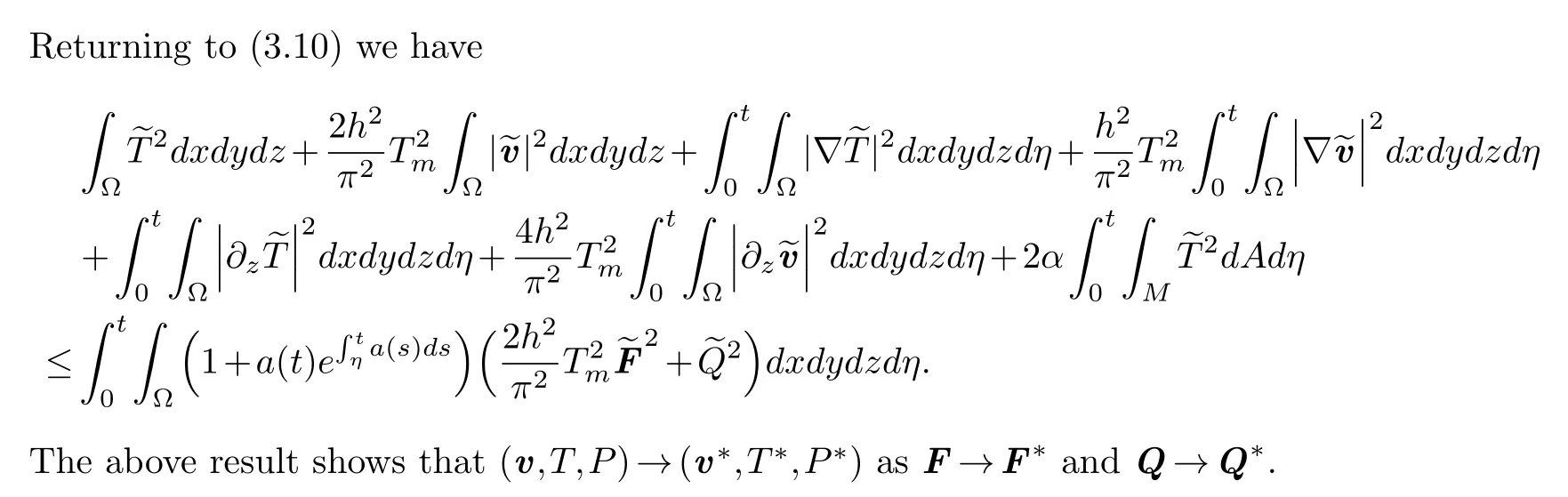
Acknowledgements

We note that the ideas developed in this paper can equally apply to other type of equations with other kinds of boundary conditions.The authors would like to deeply thank all the reviewers for their insightful and constructive comments.