Batalin-Vilkovisky Structure on Hochschild Cohomology of Self-Injective Quadratic Monomial Algebras

( School of Mathematics and Statistics, Henan University, Kaifeng 475004, China)

Abstract: We give a complete description of the Batalin-Vilkovisky algebra structure on Hochschild cohomology of the self-injective quadratic monomial algebras.

Keywords: Batalin-Vilkovisky algebra structure; Hochschild cohomology; Self-injective quadratic monomial algebra

§1.Introduction

The Hochschild homology and cohomology theory played a fundamental role in representation theory of artin algebras.Hochschild homology is closely related to the voriented cycle and the global dimension of algebras; Hochschild cohomology is closely related to simple connectedness,separability and deformation theory.

The monomial algebras is a class of relatively simple algebras.The Hochschild homology and cohomology of this kind of algebras have been widely studied.The cup product on the Hochschild cohomology has been described for some especial monomial algebras such as radical square zero algebras [3], exterior algebras [14], truncated quiver algebras [1,7]and so on.For the Lie structure on the Hochschild cohomology, Xu and Zhang have described the Gerstenhaber bracket on the Hochschild cohomology of truncated quiver algebras in terms of parallel paths[15].The Gerstenhaber bracket on the Hochschild cohomology of triangular quadratic monomial algebras are considered in [2].However, for most finite dimensional algebras, it is little to known about the the Gerstenhaber bracket of the Hochschild cohomology.Here we will give the description of the Gerstenhaber bracket on Hochschild cohomology of the self-injective quadratic monomial algebras clearly.

During several decades,a new structure in Hochschild theory has been extensively studied in topology and mathematical physics, and recently this was introduced into algebra, the so-called Batalin-Vilkovisky structure.Roughly speaking a Batalin-Vilkovisky structure is an operator on a Gerstenhaber algebra which squares to zero, and which together with the cup product,can express the Gerstenhaber bracket.A Batalin-Vilkovisky algebra structure exists only on Hochschild cohomology of certain special classes of algebras.Tradler found that the Hochschild cohomology of a finite-dimensional self-injective algebra is a Batalin-Vilkovisky algebra [11].In 2016, Lambre et al.and Volkov independently showed that this result is also valid for Frobenius algebras with semisimple Nakayama automorphisms [8,13].But it is very difficult to give the Batalin-Vilkovisky algebra structure on the Hochschild cohomology of an algebra in general.Here for the self-injective quadratic monomial algebras, we can give a complete description of the Batalin-Vilkovisky algebra structure on the Hochschild cohomology of this kind of algebras.

The paper is structured as follows.In Section 2, we review the definitions of Hochschild cohomology, cup product, Gerstenhaber bracket product and Batalin-Vilkovisky algebra.In Section 3, we first show that the self-injective quadratic monomial algebras are essentially the radical square zero Nakayama algebras of typeWe denote this class of algebras byAnand recall the minimal projective bimodule resolution ofAnwhich has given by Bardezll.We also give a basis of each degree of Hochschild cohomology ofAnby using this resolution.In Section 4, we give the ring structure onHH*(An)=HHm(An).In particular, we show that the Hochschild cohomology ring modulo the nilpotent ideal is finite generated, and so give a positive answer to the Snashall-Solberg conjecture.In Section 5, by the chain mappings between the reduced bar resolution and the minimal projective bimodule resolution ofAn,we give the Gerstenhaber algebra structure and the Batalin-Vilkovisky algebra structure onHH*(An) clearly.Throughout this paper, we fix k an algebraically closed field with chark=0,⊗:=⊗k.

§2.Hochschild cohomology of associative algebras

The cohomology theory of associative algebras was introduced by Hochschild (see [6]).Let Λ be an associative algebra over a field k.The Hochschild cohomologyHH*(Λ) of Λ has a very rich structure.In this section, we recall the cup product, the Gerstenhaber bracket and Batalin-Vilkovisky algebra structure in the Hochschild cohomology.

For an associative k-algebra Λ, there is a projective bimodule resolution of Λ as following:

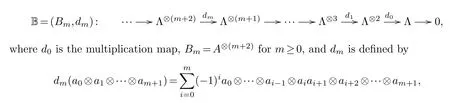
for alla0,a1,···,am+1∈Λ.This resolution is called the bar resolution of Λ.

This graded Lie bracket is usually called the Gerstenhaber bracket inHH*+1(Λ).It is well-known that (HH*(Λ),凵,[,]) is a Gerstenhaber algebra (see [5]).That is, the following conditions hold:

(1) (HH*(Λ),凵) is an associative algebra.

(2) (HH*+1(Λ),[,]) is a graded Lie algebra with bracket [,]of degree-1.

(3) [f 凵g,h]=[f,h]凵g+(-1)|f|(|h|-1)f 凵[g,h], where|f|denotes the degree off.

If there is an operator on Hochschild cohomology which squares to zero and together with the cup product can express the Lie bracket, then it is an Batalin-Vilkovisky algebra.Let us review the definition of Batalin-Vilkovisky algebra (see, for example [12]).

Definition 2.1.A Batalin-Vilkovisky algebra is a Gerstenhaber algebra(Λ·,凵,[,])together with an operatorΔ:Λ·→Λ·-1of degree -1such thatΔ◦Δ=0and

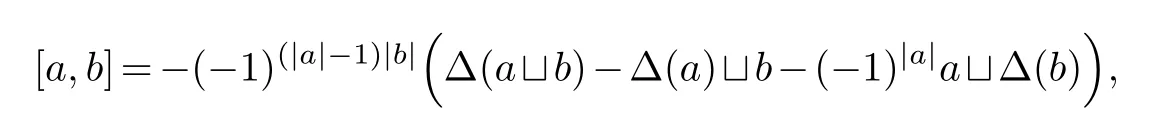
for homogeneous elements a,b∈Λ·.

For any associative k-algebra with unity,the author proved that(HH*(Λ),凵,[,])is always a Gerstenhaber algebra in [5].However, for a given algebra, it is very difficult to obtain this structure concretely, that is, to describe exactly the cup product and Gerstenhaber bracket product, is very difficult.The Batalin-Vilkovisky operator Δ does not always exist for the Hochschild cohomology ringHH*(Λ) of an algebra Λ.So far, we only know that there is a Batalin-Vilkovisky operator on Hochschild cohomology ring for few kinds of algebras.

§3.Hochschild cohomology groups

In this section, we consider the Hochschild cohomology groups of the self-injective quadratic monomial algebras.Recently, Lu and Zhu have given a detailed description of self-injective quadratic monomial algebras in [9].They have shown that a basic k-algebra Λ over an algebraically closed field k is self-injective if and only if Λ is self-injective Nakayama k-algebra(see Remark 4.3.7 in [9]).Thus by studying the self-injective quadratic monomial algebras, we only need to consider the algebrasAn, which are given by quiverQas following:

with relationsαiαi+1=0,i=1,2,···,n, whereαn+1=α1.This is,An=kQ/I, whereIis an ideal of path algebra kQgenerated byαiαi+1=0,i=1,2,···,n.We denote byeithe trivial path inQand the idempotent element in kQcorresponding to vertexi,i=1,2,···,n.ThenB:={ei,αi|1≤i≤n}is a k-basis ofAn, and so that dimkAn=2n.

The algebrasAnare truncated quiver algebras.Bardezll and his collaborators have given the Hochschild cohomology groups for truncated quiver algebras in [4].In this section we will use the parallel paths to give these conclusions again.Firstly, we consider the minimal projective bimodule resolution ofAn.Setting

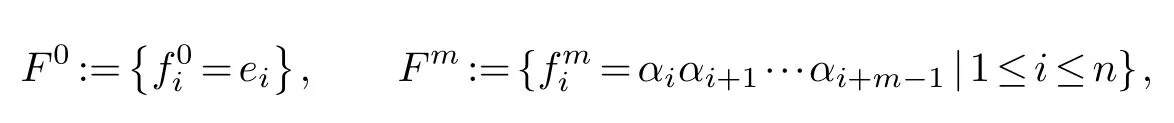
for allm≥1.We denote by o(p) and t(p) the originals and terminus ofp, for any pathp∈kQ.Let

and denote by k{X//Y}the vector space spanned by the elements inX//Y, and call (p,q)∈kQ//kQa parallel path.Consider the setsB//Fm, we get

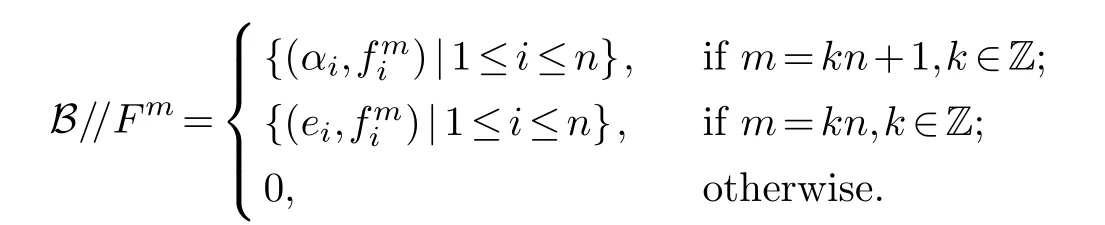
Define complex L=(Lm,σm),whereLm=k(B//Fm)ifm≥0 and for anym≥1,σm:Lm-1→Lmis given by

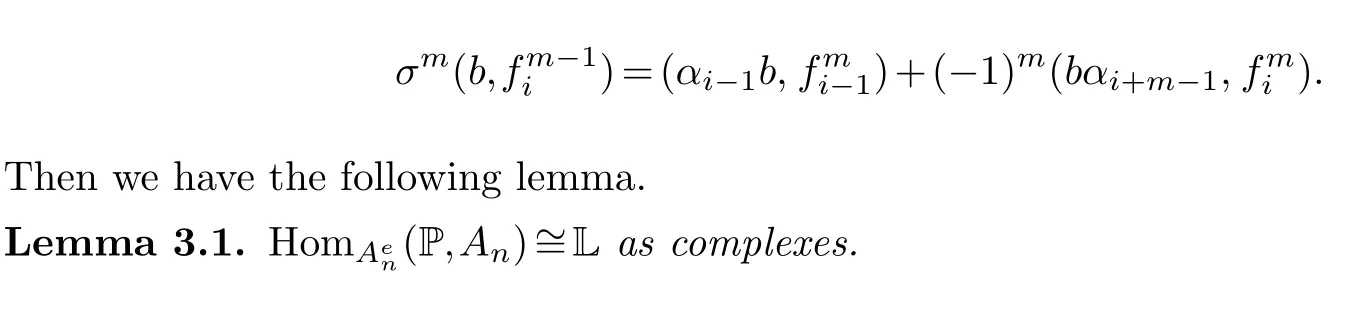
andσm=0 ifm/=kn+1.Then,by direct calculation,we get a k-basis ofHHm(An)as following.

Proposition 3.1.Let An be the self-injective quadratic monomial algebra.Then

§4.Hochschild cohomology ring

In this section,the cup product of the cohomology ringHH*(An)is described by the parallel paths, and so that the ring structure ofHH*(An) andHH*(An)/Nare given explicitly.

For any finite-dimensional k-algebra Λ, Siegel and Witherspoon proved that any projective Λe-resolution X of Λ gives rise to the cup product onHH*(Λ)=HHm(Λ) (see [11]).They showed that there exists a chain map△:X→X⊗ΛX lifting the identity, which is unique up to homotopy, and the cup product of two elementsηinHHm(Λ) andξinHHn(Λ) can be defined by the composition of the maps

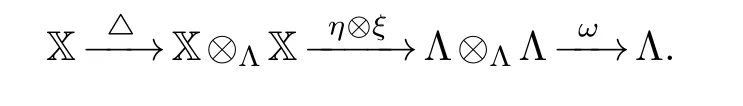
whereωis the natural isomorphism.

Here, we will use the minimal projective bimodule resolution P=(Pm,dm) ofAnwhich is constructed in Section 3, to give the cup product ofHH*(An).First recall that the tensor complex P⊗AnP:=(Pm,bm) is given by

where b0=ω◦(d0⊗d0), d0is the multiplication map, ω:An ⊗An An →An is the natural isomorphism.

Proof.Firstly, it is easy to see thatd0=b0◦△0.Secondly, forn=1 and eachαi, we have

The dreams come nightly. Dreams of turning cartwheels in the yard or hitting a tennis ball against a brick wall. But there is one, the most vivid and recurring13, and the most haunting of all...There is a lake and trees, a soft breeze and a perfect sky. It is a scene so beautiful it is almost beyond imagining. And in the midst of it all, she is walking. She has never felt more at peace.

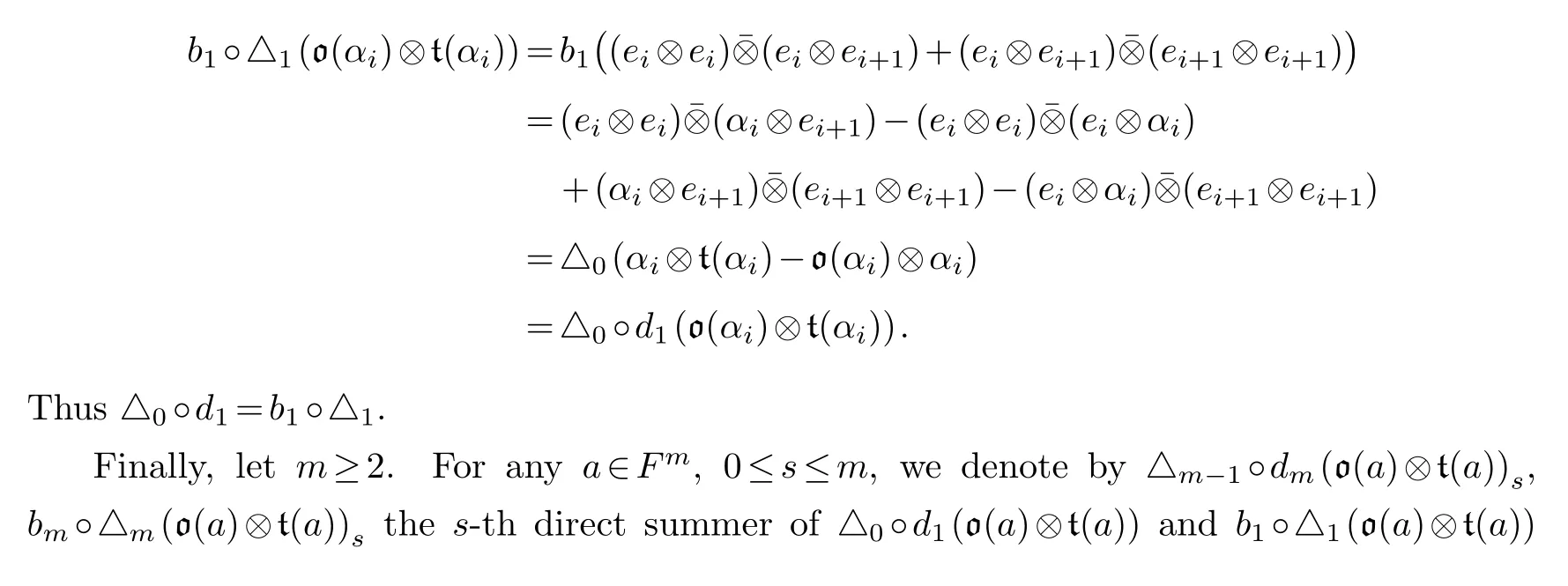
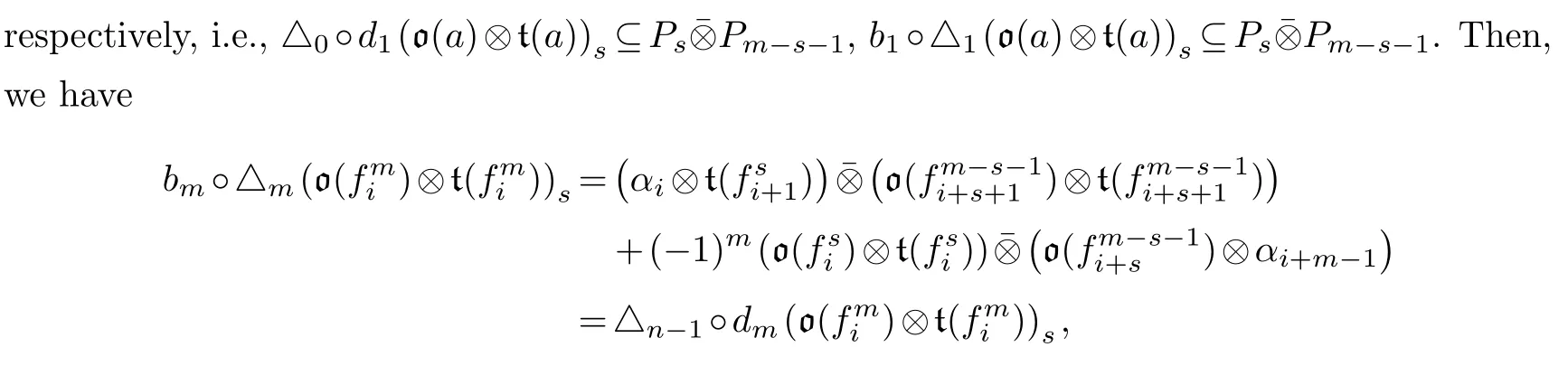
Therefore, we obtain the commutative diagram.

Now, for anym≥0 andη:=(a,f)∈Lm=k{B//Fm}, we identify it with its imageφm(η)under the isomorphismφm:Lm →which is given in Section 3.By the morphism△:=(△m)m≥0,the following theorem will give a description of the cup product using the parallel paths.

Proposition 4.1.Suppose η:=(a,f)∈HHm(An)and ξ:=(a′,f′)∈HHl(An).Then

Now, using the basis ofHHm(An) in the pervious section and the description of the cup product in Proposition 4.1, we can give the ring structure ofHH*(An).

Theorem 4.1.As gradedk-algebras, we have the following isomorphism:

For any finite-dimensional k-algebra Λ, letNbe the ideal ofHH*(Λ) generated by all the homogeneous nilpotent elements.IfHH*(Λ)/Nis a finite-dimensional commutative k-algebra,then it is used to define the support varieties for Λ-modules[10].Moreover, Snashall and Solberg conjectured thatHH*(Λ)/Nis finitely generated for any finite-dimensional k-algebra Λ.Here,using the result in Theorem 4.1, we can give the ring structure ofHH*(An)/Ndirectly.

Corollary 4.1.For the quotient algebra HH*(An)/N, we have

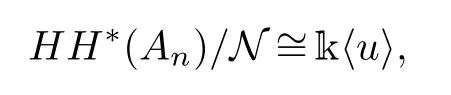
where the degree of u is kn and kn is even.

§5.Batalin-Vilkovisky structure on Hochschild cohomology

In this section, we give the Gerstenhaber algebra structure and the Batalin-Vilkovisky algebra structure onHH*(An) clearly.

whereen+1=e1andαn+1=α1.In [8]and [13], the authors proved that the Hochschild cohomology ring of a Frobenius algebra with semisimple Nakayama automorphism is a Batalin-Vilkovisky algebra in different ways.For the algebraAn, we can define an automorphism ¯()by

for anyα∈HHm(An), whereB1={ei|1≤i≤n}andμ=(-1)i(m-1).

By the formulas

This means that to determine operator Δ, we only need to calculate Δ(a) and Δ(a凵b) for all the generatorsa,bofHH*(An).Moreover, using the comparison morphisms Ψ and Φ, we compute Δ(f) by formula Δ(f)=Δ(f ◦Ψm)Φm-1,for anyf ∈HHm(An).

Theorem 5.1.Let An be the self-injective quadratic monomial algebra.Denote byΔthe Batalin-Vilkovisky operator on HH*k〈y,u〉/I.Then we have

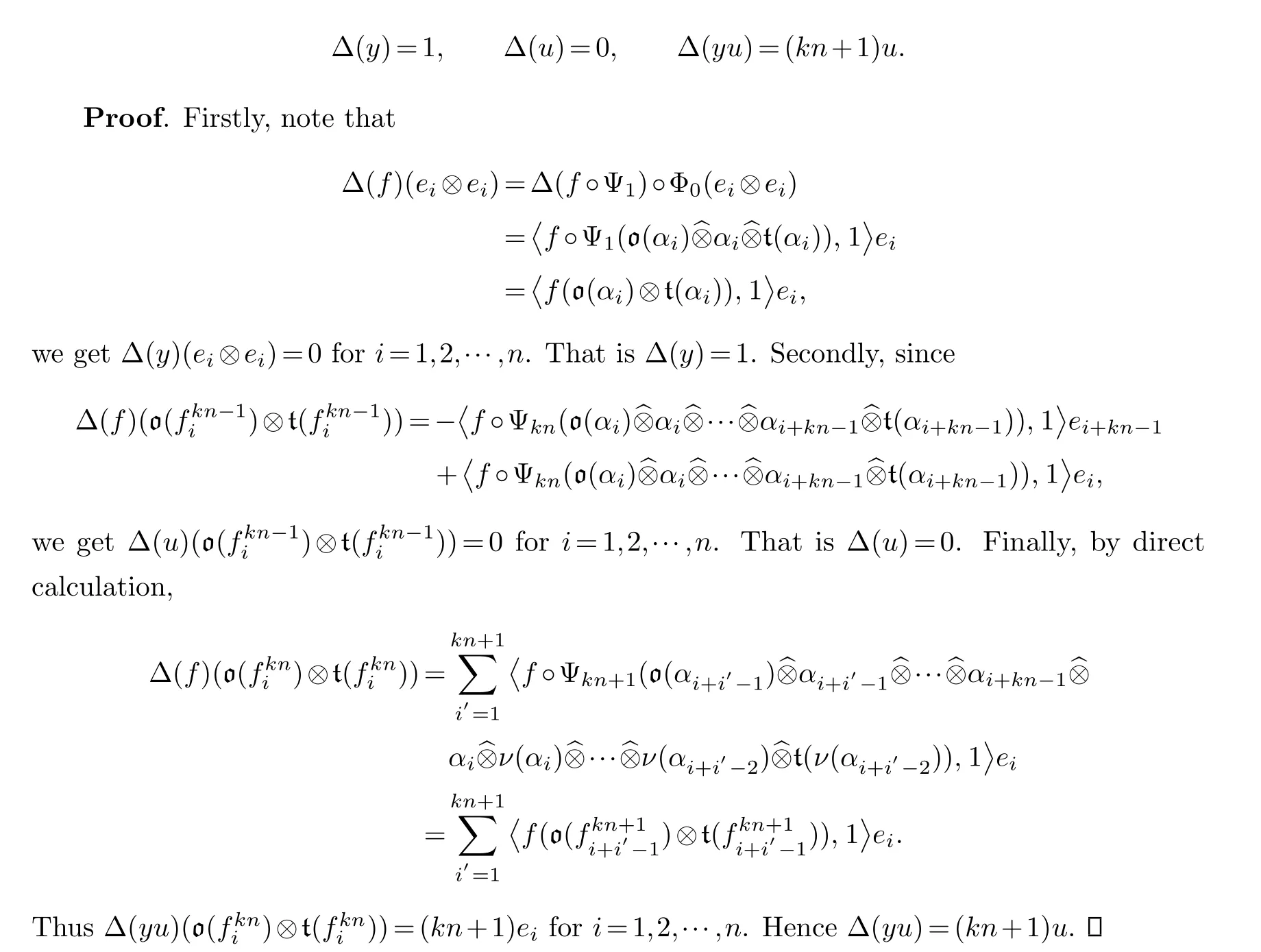
Using the Batalin-Vilkovisky operator Δ onHH*(An), we can determine the Gerstenhaber bracket [,]onHH*(An) by setting

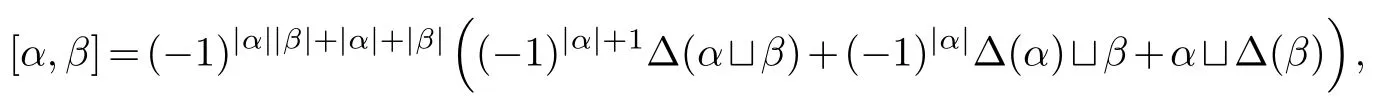
for any homogeneous elementsα,β ∈HH*(An).Then the Gerstenhaber algebra structure onHH*(An) can be induced.

Corollary 5.1.Let An be the self-injective quadratic monomial algebra.Then Gerstenhaber bracket on the HH*(An)k〈y,u〉/I is induced by

Now we can give a complete description of the Batalin-Vilkovisky algebra structure on Hochschild cohomology of the self-injective quadratic monomial algebras.

Corollary 5.2.Let An be the self-injective quadratic monomial algebra.The Batalin-Vilkovisky algebra(HH*(An), 凵,[,],Δ)is isomorphic tok〈y,u〉/I, where the ideal I is generated by y2and yu-uy, the Gerstenhaber bracket is induced by[y,y]=0,[u,u]=0,[y,u]=-knu, the Batalin-Vilkovisky operator is induced byΔ(y)=1,Δ(u)=0,Δ(yu)=(kn+1)u, and the degree of y and u is 1 and kn respectively, kn is even.