Y-Gorenstein Cotorsion Modules

(Department of Mathematics, Longnan Teachers College, Longnan 742500, China)

Abstract: Let R be an associative ring with identity,and Y be a class of right R-modules,which contains all injective right R-modules.In this paper, we introduce the definition of Y-Gorenstein cotorsion modules, which is a generalization of cotorsion and Gorenstein cotorsion modules.We discuss the relationship between Gorenstein cotorsion, weakly Gorenstein cotorsion and Y-Gorenstein cotorsion modules.We investigate properties and characterizations of Y-Gorenstein cotorsion modules.

Keywords: Y-Gorenstein cotorsion; Y-Gorenstein flat; Strongly Gorenstein flat; Weakly Gorenstein cotorsion; Coherent ring

§1.Introduction

Gorenstein homological theory plays an important role in relative homological algebra.In 2001, Enochs et al [5]introduced Gorenstein flat modules over an associative ringR, which is an important generalization of flat modules.Lei and Meng [7]investigated Gorenstein cotorsion modules relative to Gorenstein flat modules, and got many properties similar to cotorsion modules.Ding et al [1]introduced and invstigated strongly Gorenstein flat modules.Based on the above, Zhao et al [12]discussed weakly Gorenstein cotorsion modules relative to strongly Gorenstein flat modules.Meng [9]gave the notion ofY-Gorenstein flat modules, in whichYis a class of rightR-modules and contains all injective rightR-modules.As is well known, flat modules areY-Gorenstein flat, andY-Gorenstein flat modules are Gorenstein flat.WhenYis the class of all injective rightR-modules,Y-Gorenstein flat modules are precisely Gorenstein flat modules.Naturally, we can consider cotorsion modules relative toY-Gorenstein flat modules,which will be calledY-Gorenstein cotorsion modules in the paper.Furthermore, we investigate the relationship between Gorenstein cotorsion modules, weakly Gorenstein cotorsion modules andY-Gorenstein cotorsion modules.

We now state main results of this paper.

Theorem 1.1.Let F be the class of all flat left R-modules, and Y be a class of right R-modules which contains all injective right R-modules.If Y+⊆F, then every Y-Gorenstein cotorsion left R-module is weakly Gorenstein cotorsion.

Theorem 1.2.The following statements hold:

(1)For a family {Mi}i∈I of R-modules, all Mi are Y-Gorenstein cotorsion if and only ifY-Gorenstein cotorsion.

(2)Let0→M →N →L→0be an exact sequence of left R-modules.If M,L are Y-Gorenstein cotorsion modules, then N is also Y-Gorenstein cotorsion.

Theorem 1.3.Let R be a right coherent ring, every left R-module has finite Y-Gorenstein flat dimension, and A be a nonempty collection of left ideals of R.Then the following statements are equivalent:

(1)Every Y-Gorenstein cotorsion module RM is A-injective.

(2)R/A is Y-Gorenstein flat for any A∈A.

Theorem 1.4.Let R be a left perfect ring.Then the following statements are equivalent:

(1)Every left R-module is Y-Gorenstein cotorsion.

(2)Every Y-Gorenstein flat left R-module is Y-Gorenstein cotorsion.

This paper is organized as follows.Section 2 contains some known notions and results for use throughout the paper, and we introduceY-Gorenstein cotorsion modules, and discuss the relationship between Gorenstein cotorsion modules, weakly Gorenstein cotorsion modules andY-Gorenstein cotorsion modules.Section 3 is devoted to properties and characterizations ofY-Gorenstein cotorsion modules.

§2.Preliminaries

Throughout the paper,Rwill be an associative ring with identity and all modules are unitalR-modules.We useR-Mod (resp., Mod-R) to denote the class of left (resp., right)R-modules.RM(resp.,MR) denotes a left (resp., right)R-moduleM.A leftR-moduleCis called cotorsion if(F,C)=0 for any flat leftR-moduleF(see [8]).Following [5], a moduleRMis said to be Gorenstein flat, if there exists an exact sequence of flat leftR-modules···→F1→F0→F0→F1→...withMKer(F0→F1), such thatE ⊗R-leaves the sequence exact for every injective rightR-moduleE.A moduleRNis called Gorenstein cotorsion if(F,N)=0 for any Gorenstein flat leftR-moduleF(see [7]).In addition, a moduleRMis said to be strongly Gorenstein flat, if there exists an exact sequence of projective leftRmodules···→P1→P0→P0→P1→...withMKer(P0→P1), such that HomR(-,F) leaves the sequence exact for every flat leftR-moduleF.WhenRis a right coherent ring,every strongly Gorenstein flat leftR-module is Gorenstein flat.A moduleRNis called weakly Gorenstein cotorsion if(F,N)=0 for any strongly Gorenstein flat leftR-moduleF(see [12]).

LetXbe a class of leftR-modules that contains all projective leftR-modules, andYbe a class of rightR-modules that contains all injective rightR-modules.According to [9], a moduleRMis said to beX-Gorenstein projective, if there exists an exact sequence of projective leftRmodules···→P1→P0→P0→P1→...withKer(P0→P1), such that HomR(-,X) leaves the sequence exact for everyX ∈X.A moduleRNis calledY-Gorenstein flat if there exists an exact sequence of flat leftR-modules···→F1→F0→F0→F1→...withMKer(F0→F1),such thatY ⊗R-leaves the sequence exact for everyY ∈Y.

Remark 2.1.(1)Y-Gorenstein flat modules are Gorenstein flat.

(2)If Y is the class of all injective right R-modules, then Gorenstein flat modules are precisely Y-Gorenstein flat modules.

(3)If X is the class of all flat modules, then the class of X-Gorenstein projective modules coincides with that of strongly Gorenstein flat modules.

LetAbe a nonempty collection of left ideals of a ringR.RMis said to beA-injective, if everyR-homomorphismf:A→MwithA∈Acan be lifted to anR-homomorphismg:R→M,or equivalently(R/A,M)=0 for anyA∈A(see [11]).

LetCbe a class of leftR-module (closed under isomorphisms).AC-precover ofRMis a morphismφ:C →MwithC ∈Csuch that HomR(C′,φ) is surjective for everyC′∈C.If in addition, any morphismα:C →Cverifyingφ◦α=φis an automorphism, thenφis said to be aC-cover ofRM(see [2]).DenoteC⊥={M ∈R-Mod=0 for anyC ∈C}, and⊥C={N ∈R-Mod(N,C)=0 for anyC ∈C}.A pair (F,C) of classes of leftR-modules is called a cotorsion theory (which is also called a cotorsion pair), ifF⊥=Cand⊥C=F(see [3]).A cotorsion theory (F,C) is complete, if for anyM ∈R-Mod, there exist short exact sequences 0→C →F →M →0 and 0→M →C′→F′→0 withF,F′∈FandC,C′∈C(see[10]).A cotorsion theory(F,C)is hereditary, if whenever 0→L′→L→L′′→0 is exact withL,L′′∈F,thenL′is also inF(see [4,6]).

Definition 2.1.Let Y be a class of right R-modules that contains all injective right R-modules.A module RM is said to be Y-Gorenstein cotorsion provided that(Q,M)=0for any Y-Gorenstein flat left R-module Q.

It is obvious that cotorsion modules and Gorenstein cotorsion modules areY-Gorenstein cotorsion.IfYis the class of all injective rightR-modules, then the class of Gorenstein cotorsion leftR-modules coincides with that ofY-Gorenstein cotorsion leftR-modules.

Lemma 2.1.[9]Let X be a class of left R-modules that contains all projective left R-modules,and Y be a class of right R-modules that contains all injective right R-modules.If Y+⊆X,where Y+={Y+=HomZ(Y,Q/Z)|Y ∈Y}, then every X-Gorenstein projective left R-module is Y-Gorenstein flat.

Proposition 2.1.Let F be the class of all flat left R-modules, and I be the class of all injective right R-modules.If I+⊆F, then any F-Gorenstein projective left R-module is I-Gorenstein flat, which means strongly Gorenstein flat modules are Gorenstein flat.

Proposition 2.2.Let F be the class of all flat left R-modules, and Y be a class of right R-modules that contains all injective right R-modules.If Y+⊆F, then every strongly Gorenstein flat left R-module is Y-Gorenstein flat.

Proof.This is not difficult to prove by Remark 2.1(3) and Lemma 2.1.

Following the above proposition,we can get the relationship betweenY-Gorenstein cotorsion leftR-modules and weakly Gorenstein cotorsion modules.

Theorem 2.1.Let F be the class of all flat left R-modules, and Y be a class of right R-modules which contains all injective right R-modules.If Y+⊆F, then every Y-Gorenstein cotorsion left R-module is weakly Gorenstein cotorsion.

According to definition of weakly Gorenstein cotorsion andY-Gorenstein cotorsion modules,it is easy to obtain that everyY-Gorenstein cotorsion leftR-module is weakly Gorenstein cotorsion.

Corollary 2.1.If R is a right coherent ring, then every Gorenstein cotorsion left R-module is weakly Gorenstein cotorsion.

§3.Properties and characterizations of Y-Gorenstein cotorsion modules

In this section,Ydenotes a class of rightR-modules that contains all injective modules.

Theorem 3.1.The following statements hold:

(1)For a family {Mi}i∈I of R-modules, all Mi are Y-Gorenstein cotorsion if and only ifis Y-Gorenstein cotorsion.

(2)Let0→M →N →L→0be an exact sequence of left R-modules.If M,L are Y-Gorenstein cotorsion modules, then N is also Y-Gorenstein cotorsion.

Proof.(1) Let{Mi}i∈Ibe a family ofR-modules.One hand, if allMiareY-Gorenstein cotorsion leftR-modules, then for anyY-Gorenstein flat leftR-moduleQ, we have the isomorphism

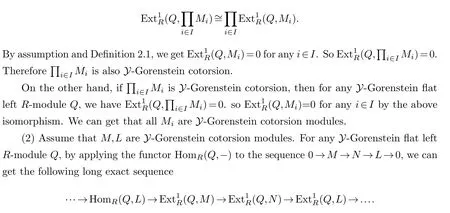
SinceM,LareY-Gorenstein cotorsion modules, we haveso=0.It is easy to obtain thatNis alsoY-Gorenstein cotorsion.

Lemma 3.1.If R is a right coherent ring, then the class of Y-Gorenstein flat left R-modules are closed under extensions, kernels of epimorphisms, direct sums and direct summands.

Theorem 3.2.Let R be a right coherent ring and RM be a Y-Gorenstein cotorsion module.Then

for any Y-Gorenstein flat left R-module Q and any i≥1.

Proof.For anyY-Gorenstein flat leftR-moduleQ, suppose···→P2→P1→P0→Q→0 is a projective resolution ofQ.LetK0=Ker(P0→Q),Kj=Ker(Pj →Pj-1) (j ≥1).Note that projective modules areY-Gorenstein flat,soPiisY-Gorenstein flat for anyi≥0.Following Lemma 3.1, we can getKjisY-Gorenstein flat for anyj ≥0.By applying the functor HomR(-,M)to above resolution, it is not difficult to obtain that

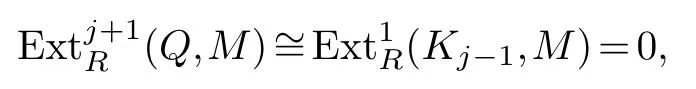
Proposition 3.1.Let R be a right coherent ring and(ε):0→M →N →L→0be an exact sequence of left R-modules.If N is Y-Gorenstein cotorsion, then the following conditions are equivalent:

(1)M is a Y-Gorenstein cotorsion module.

(2) (ε)stays exact underHomR(Q,-)for any Y-Gorenstein flat module Q.

Proof.(1)⇒(2) It is obvious.

(2)⇒(1) For anyY-Gorenstein flat moduleQ, By applying the functor HomR(Q,-) to the sequence (ε), we can get the following long exact sequence

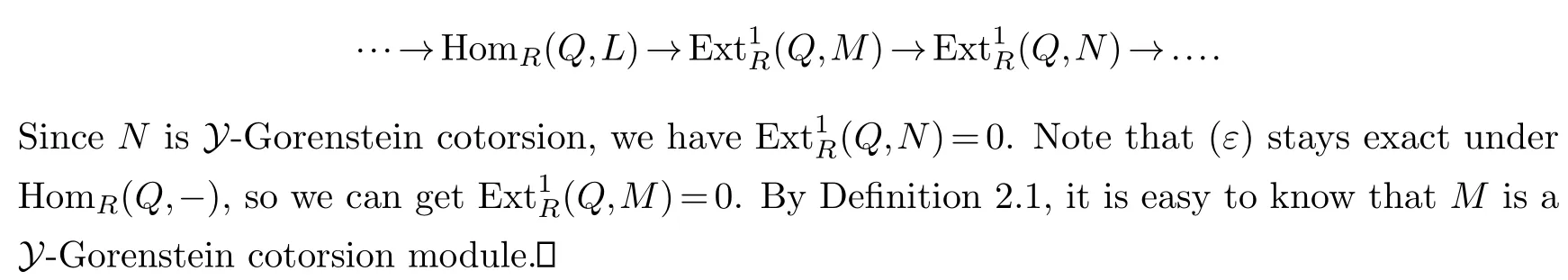
Corollary 3.1.Let M be a right R-module with finite injective dimension.ThenHomZ(M,Q/Z)is Y-Gorenstein cotorsion module.

Proof.Since Gorenstein cotorsion modules areY-Gorenstein cotorsion, it is not difficult to prove above conclusion by Proposition 2.4 in [7].

Denote byYGF(resp.,YGC) the class of allY-Gorenstein flat (resp., cotorsion) leftR-modules.By ( [9],Theorem 4.13), we can get the following result.

Lemma 3.2.If R is a right coherent ring and every left R-module has finite Y-Gorenstein flat dimension.Then(YGF,YGC)is a complete hereditary cotorsion theory.

Theorem 3.3.Let R be a right coherent ring, every left R-module has finite Y-Gorenstein flat dimension, and A be a nonempty collection of left ideals of R.Then the following statements are equivalent:

(1)Every Y-Gorenstein cotorsion module RM is A-injective.

(2)R/A is Y-Gorenstein flat for any A∈A.

Proof.(1)⇒(2) For anyA∈A, it is sufficient to prove(R/A,C)=0 for everyYGorenstein cotorsion moduleC.Consider the exact sequence 0→A→R→R/A→0 and induced exact sequence

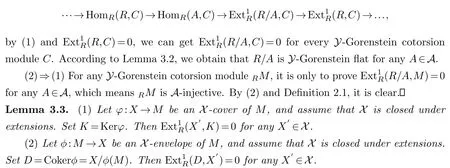
Theorem 3.4.Let R be a right coherent ring, and Q be a Y-Gorenstein flat cover of RM with K=Ker(Q→M).Then K is a Y-Gorenstein cotorsion module.Moreover, if M is a Y-Gorenstein cotorsion module, then Q is also a Y-Gorenstein cotorsion module.

Proof.According to Lemma 3.1 and Lemma 3.3(1),it can be obtained that(X′,K)=0 for anyY-Gorenstein flat moduleX′.ThenKis aY-Gorenstein cotorsion module by Definition 2.1.Moreover, ifMis aY-Gorenstein cotorsion module, thenQis also aY-Gorenstein cotorsion module by properties of the Ext functor.

Theorem 3.5.Let R be a right coherent ring, and H be a Y-Gorenstein cotorsion envelope of RM with D=Coker(M →H).Then C is a Y-Gorenstein flat module.Moreover, if M is a Y-Gorenstein flat module, then H is also a Y-Gorenstein flat module.

Proof.It is not difficult to prove by Theorem 3.1 (2) and Lemma 3.3 (2).

Proposition 3.2.Let R be a commutative ring and P a flat R-module.If M is a Y-Gorenstein flat module, then M ⊗R P is a Y-Gorenstein flat module.

Proof.Assume thatMis aY-Gorenstein flat module, then there exists an exact sequence of flatR-modules

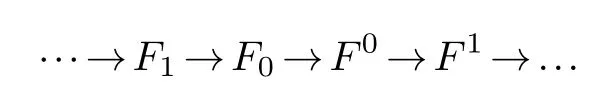
withsuch thatY ⊗R-leaves the sequence exact for anyY ∈Y.SincePis a flat module, we have exact sequence

withNote thatFi,Fiare flat for alli≥0 andPis a flat module, we know thatFi ⊗R P, Fi ⊗R Pare flat modules.For anyY ∈Y, consider the following commutative diagram (Diagram 1)

Diagram 1 the constructed commutative diagram

SinceMisY-Gorenstein flat andPis flat, it is not difficult to obtain that the upper sequence of commutative diagram is exact.ThereforeM ⊗R Pis aY-Gorenstein flat module.

Theorem 3.6.Let R be a left perfect ring.Then the following statements are equivalent:

(1)Every left R-module is Y-Gorenstein cotorsion.

(2)Every Y-Gorenstein flat left R-module is Y-Gorenstein cotorsion.

Proof.(1)⇒(2) It is obvious.

(2)⇒(1)For any leftR-moduleM, it is only to prove=0 for anyY-Gorenstein flat moduleQ.By the definition of theY-Gorenstein flat modules, there is an exact sequence of flat leftR-modules

withKer(F0→F1) such thatY ⊗R-leaves the sequence exact for anyY ∈Y.LetK=Ker(F1→F2), consider the short exact sequence 0→Q→F0→K →0, it is clear thatKisY-Gorenstein flat.Following (2), we knowQisY-Gorenstein cotorsion, and=0.By applying the functor HomR(K,-) to the sequence, we can get exact sequence

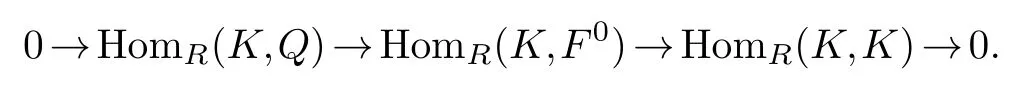
SoQis direct summand ofF0.Since the class of all flat modules is closed under direct summands,Qis flat.Note thatRis a left perfect, the class of all flat modules coincides with that of all projective modules, we have thatQis projective.So=0.Therefore,EveryY-Gorenstein flat leftR-module isY-Gorenstein cotorsion.

Acknowledgements

We thank the referees and reviewers for their time and comments.