Locally Conformal Pseudo-Kähler Finsler Manifolds

( School of Mathematics and Statistics, Henan University, Kaifeng 475004, China)

Abstract: In this paper, we give a necessary and sufficient condition for a strongly pseudoconvex complex Finsler metric to be locally conformal pseudo-Kähler Finsler.As an application, we find any complete strongly convex and locally conformal pseudo-Kähler Finsler manifold,which is simply connected or whose fundamental group contains elements of finite order only, can be given a Kähler metric.

Keywords: Strongly pseudoconvex complex Finsler metric; Locally conformal pesudo-Kähler Finsler metric; Kähler metric

§1.Introduction

In the terminology of Weyl, the projective and conformal properties of a Finsler space determine its metric relationships uniquely [7,10].Hence, it is a key subject to study conformal transformations of Finsler metrics.Recently,there are some results on conformal transformations of complex Finsler metrics, for examples [2–6,9].This present paper is concerned with a necessary and sufficient condition for a strongly pseudoconvex complex Finsler metric to be locally conformal pseudo-Kähler Finsler.

SupposeMis ann-dimensional complex manifold.Letπ:T1,0M →Mbe the holomorphic tangent bundle ofM.Assume thatz=(z1,···,zn) is a local complex coordinate system onM,then locally an elementv ∈T1,0Mis written as

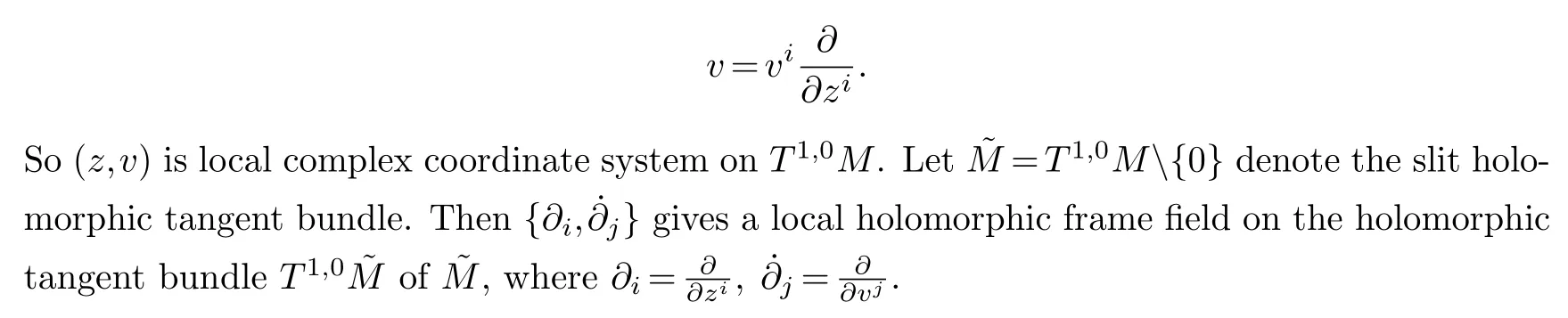
Definition 1.1.[1]A complex Finsler metric on a complex manifold M is a continuous function F:T1,0M →R+satisfying:

LetDbe the Chern-Finsler connection of a complex Finsler manifold (M,F).The Chern-Finsler connection was first introduced in [8].Its connection 1-forms are given by

Forn=1,every 1-dimensional complex Finsler manifold is pseudo-Kähler.Hence,we assume dimC(M)=n≥2 in this paper.

Main Theorem.Let(M,F)be an n-dimensional strongly pseudoconvex complex Finsler manifold.Then F is a locally conformal pseudo-Kähler Finsler metric if and only if

§2.Proof of the main theorem

which is a conformal invariant.Differentiating the equation (2.3) byz-coordinates and using the fact [∂i,∂j]=[∂i,∂¯j]=0, then we get the following two conformal invariants:

Contracting on indicesiandjin (2.6) yields (n-1)ρk=0, which impliesρk=0, namely,ρis a constant, which means the conformal transformation is a homothety.

In the following, assume thatFis not a pseudo-Kähler Finsler metric when considering locally conformal pseudo-Kähler Finsler metrics.

Lemma 2.1.Suppose the conformal invariantvanishes.If n＞2, then aij=0.

Proof.By the expression ofin (2.1), we have

Differentiating on both sides of the equation (2.7) by∂h, we have

Similarly, we get

It follows from (2.14) thatajh=0 whenn＞2.

Lemma 2.2.Suppose the conformal invariant vanishes.If n＞2, then ai¯j=0.

Proof.Since

By (1.2) - (1.4), we have

§3.An application

Define a functionF◦:TRM →R+by

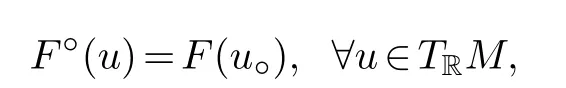
where◦:TRM →T1,0Mis given by

andJis the complex structure.

Definition 3.1.[1]We shall say that the complex Finsler metric F is strongly convex if F◦is a Riemann-Finsler metric.

Now we assume that (M,F) is a complete strongly convex complex Finsler manifold.ThenFandF◦have the same geodesics and induce the same distance function onM.We can see any two points onMcan be joined by a minimizing geodesic because of Hopf-Rinow Theorem in the Riemann-Finsler manifolds.

Proposition 3.1.[12]Given a geodesic c0:[0,l]→M joining p and q in M, there is a C1-variation α:[0,1]×(-∈,∈)→M of c0, such that

Westlake proved a global theorem on locally conformal Kähler manifolds.

Theorem 3.1.[11]A locally conformal Kähler manifold, which is simply-connected or whose fundamental group contains elements of finite order only, can be given a Kähler metric.

Hence, the following global theorem is obtained.

Theorem 3.2.Any complete strongly convex and locally conformal pseudo-Kähler Finsler manifold, which is simply connected or whose fundamental group contains elements of finite order only, can be given a Kähler metric.