Blow-Up Result for a Semi-Linear Wave Equation with a Nonlinear Memory Term of Derivative Type

(1.College of Data Science, Guangzhou Huashang College, Guangzhou 511300, China; 2.Guangdong AIB Polytechnic College, Guangzhou 510507, China)

Abstract: In this paper,we study the blow-up of solutions to a semi-linear wave equation with a nonlinear memory term of derivative type.By using methods of an iteration argument and differential inequalities, we obtain the blow-up result for the semi-linear wave equation when the exponent of p is under certain conditions.Meanwhile, we derive an upper bound of the lifespan of solutions to the Cauchy problem for the semi-linear wave equation.

Keywords: Semi-linear wave equation; Blow-up; Nonlinear memory term of derivative type; Lifespan

§1.Introduction

In this paper, we consider the following semi-linear wave equation with a nonlinear memory term of derivative type:

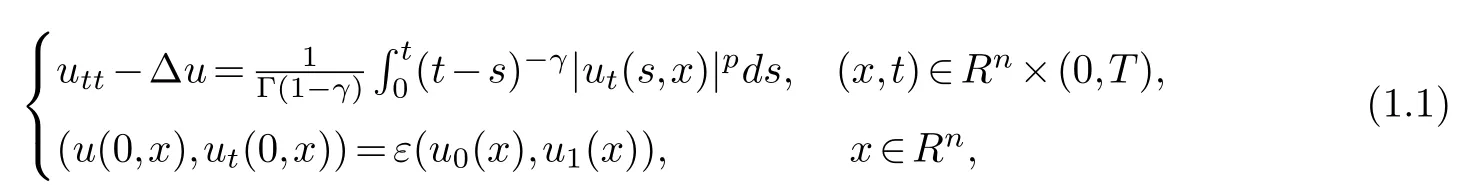
wherep＞1, Γ denotes the Euler integral of the second kind,γ ∈(0,1) andε＞0 is a parameter describing the size of initial data.

In the past few years, there have been a few papers (see [1,15,19–21,23,25,28,31–36,38–42])studying the semi-linear wave equation of the form

wheref(x,t)=|u|porf(x,t)=|ut|p.

In these papers, authors considered the existence and nonexistence of global solutions to the Cauchy problem by mainly using Kato’s type lemma and assumed initial data.Furthermore,they derived the upper or lower bound lifespan of solutions.

In[7],the authors discussed the following semi-linear wave equation with a nonlinear memory term

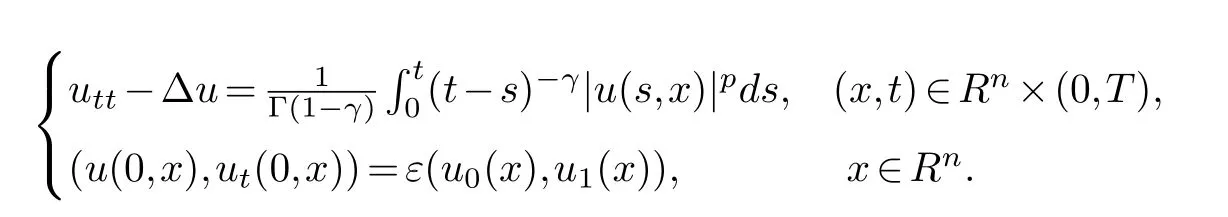
By meas of iterative techniques, they obtained the Strauss exponent, which played a key role in the existence and nonexistence of global solutions to the Cauchy problem for semi-linear wave equations.In addition, they derived the upper bound of lifespan of the solutions in subcritical and critical cases, respectively.We refer readers to more papers of semi-linear wave equations with nonlinear memory terms (see [2,3,5,12–14,17,18,22]).As for study on blow-up phenomena for the other PDEs, papers (see [4,6,8–11,16,24,26,27,29,30,37]) and references cited therein can been seen.

In this paper, we are interested in the blow-up of solutions to the Cauchy problem (1.1),which, up to the knowledge of the authors, has not been yet studied.Our goal in this paper is to show the blow-up in finite time of local in time solutions to (1.1) in the subcritical case 1＜p＜p0(n,γ) under certain assumptions on initial data.By introducing suitable functionals and applying methods of iteration arguments and differential inequalities, we obtained the Glassey exponent in the subcritical case and the upper bound lifespan of the solutions as well.

This paper is organized as follows.In Section 2, we introduce the main result.In Section 3,we are going to prove the main theory.

§2.Main result

First, we introduce the definition to an energy solution to the Cauchy problem (1.1).

Definition 2.1.Let(u0,u1)∈H1(Rn)×L2(Rn).We say that u is an energy solution of(1.1)on[0,T)if u∈C([0,T),H1(Rn))∩C1([0,T),L2(Rn))such that ut([0,T)×Rn)satisfiesu(0,·)=εu0in H1(Rn)and the integral relations

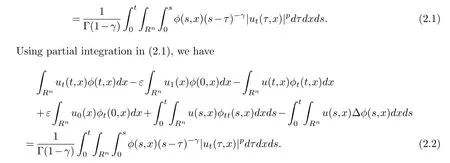
Lettingt→T, we can find thatusatisfies the definition of weak solution to (1.1).In this paper,we have the following result:

Theorem 2.1.Let us consider p＞1such that

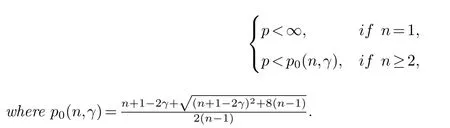
Let (u0,u1)∈H1(Rn)×L2(Rn) be nonnegative and compactly supported functions with supports contained inBRfor someR＞0 such thatu0oru1is not identically zero.Ifuis the energy solution to (1.1) with lifespanT(ε) satisfying suppu(t,·)⊂Bt+Rfor anyt∈(0,T),there exists a positive constantε0=ε0(u0,u1,n,p,γ,R), such that the solutionublows up in finite time whenε∈(0,ε0].Furthermore, we can get the upper bound estimate for the lifespan, that is

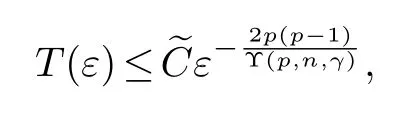
where Υ(p,n,γ)=2+(n+1-2γ)p-(n-1)p2,＞0 is a constant independent ofε.

§3.Upper bound estimate for the blow-up time

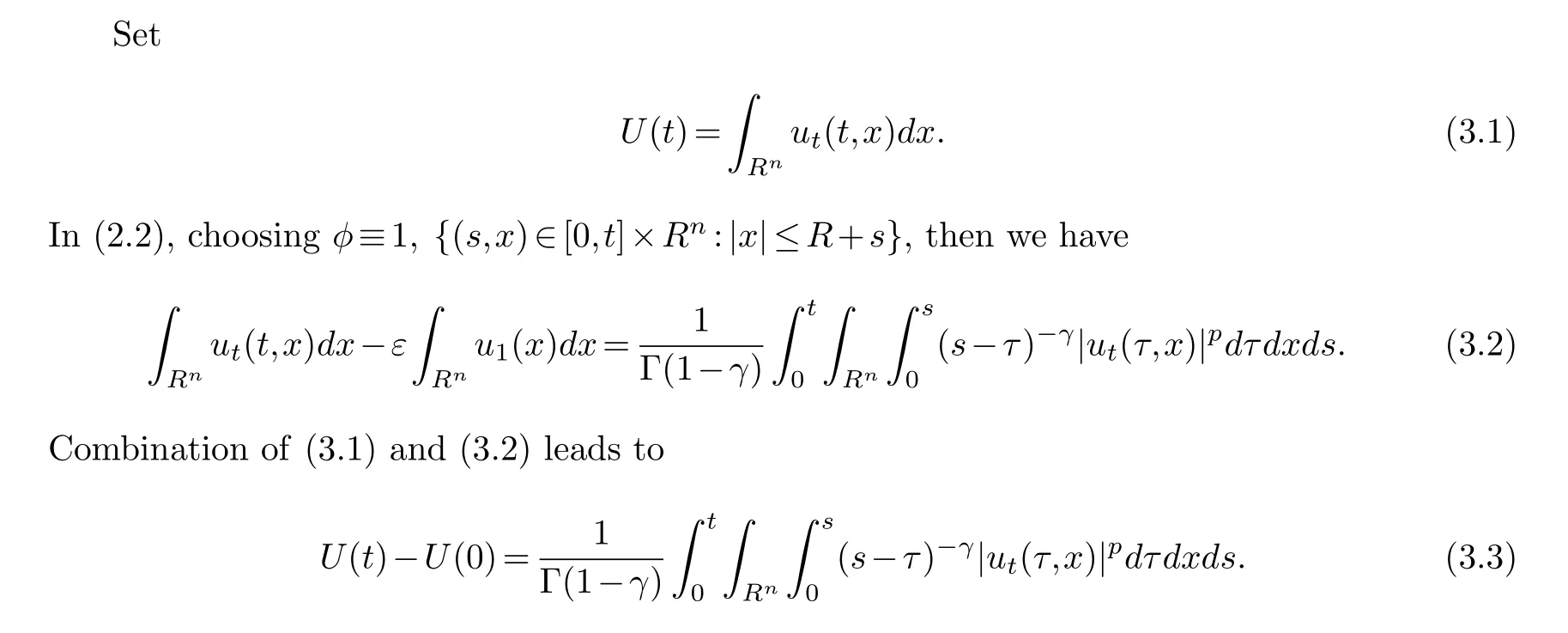
Then, we have

By Hölder inequality, we obtain

whereC ＞0.

Substituting (3.5) into (3.4), we deduce

Here, (3.6) gives an iteration frame.Next, we are going to find a first lower bound ofU(t).For this purpose, we introduce a function [39]of the form:

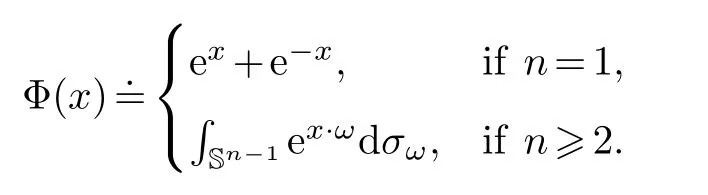
The function Φ is a positive smooth function and has following properties

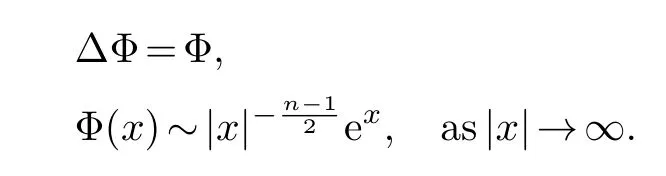
We define a function with separate variables Ψ=Ψ(t,x)=e-tΦ(x).So Ψ is the solution to Ψtt-ΔΨ=0.By using the asymptotic behavior of Ψ [23], we can get that there exists a constantC1=C1(n,R)＞0 satisfying

Using Ψ as test function in (2.2), we get for anyt∈(0,T)

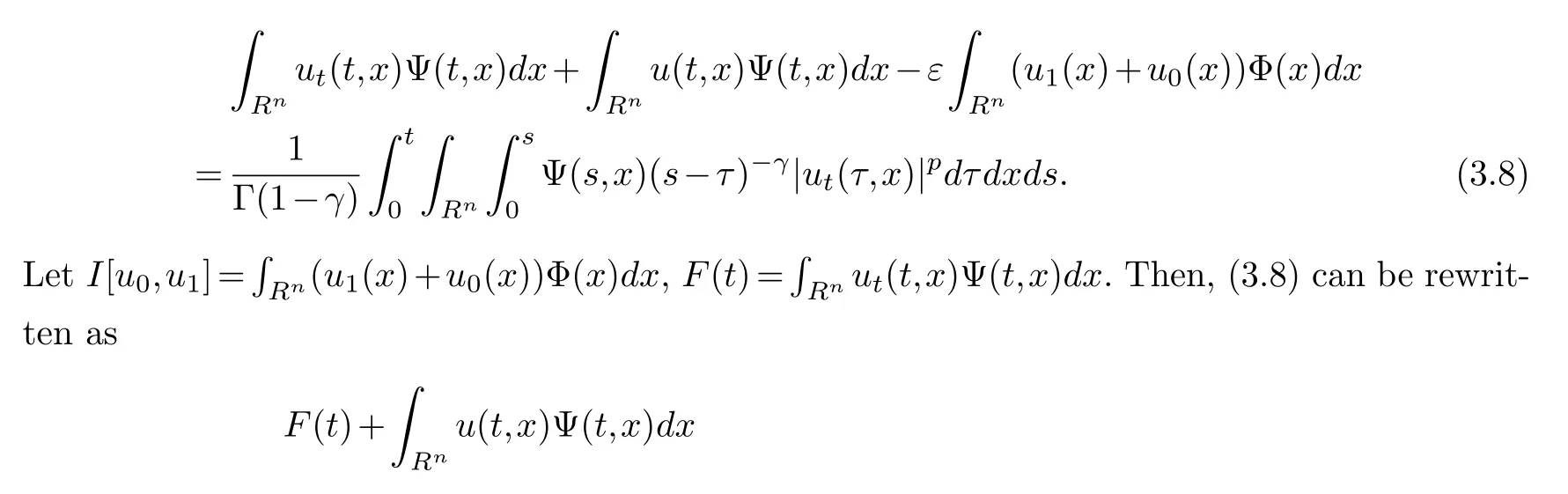
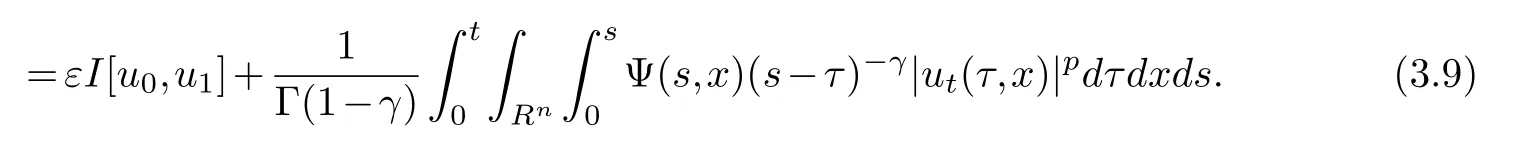
Differentiating (3.9) with respect tot, we have

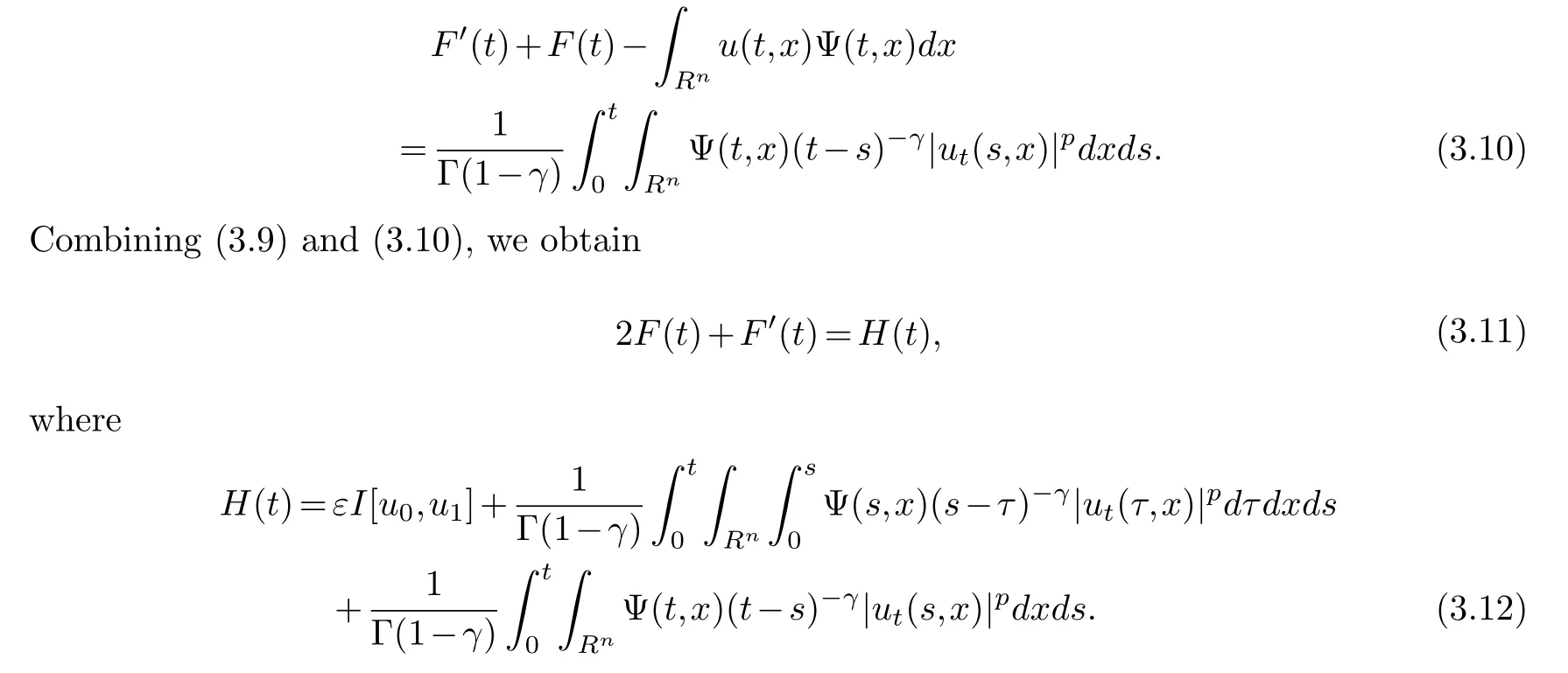
From (3.12), we haveH(t)≥0.

From (3.11) and (3.12), we can deduce

Next, we will get the blow-up result by applying (3.6) to derive a sequence of lower bounds forU(t).That is, we prove that

where{Kj}j∈N,{αj}j∈Nand{γj}j∈Nare sequences of nonnegative real numbers.

We assume that (3.17) holds forj ≥0.Next, we will prove (3.17) forj+1.

Using (3.6) and (3.17) , we have

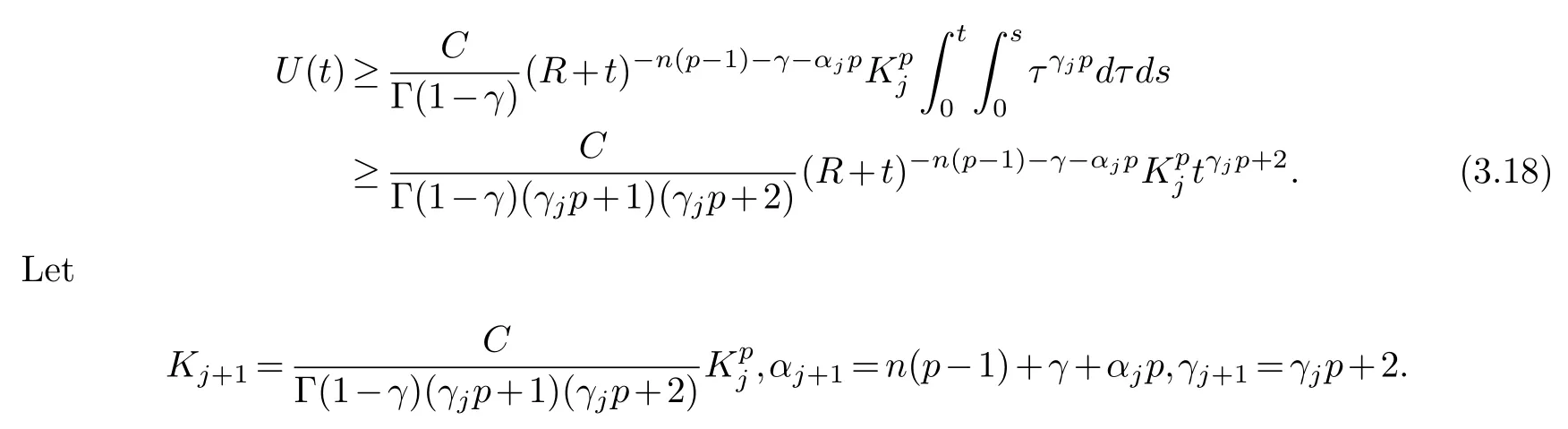
Therefore, we have proved (3.17) forj+1.

By recursive relations forαjandγj, we have

whereE=E(n,p,γ).

Combining (3.17), (3.19) and (3.22), we obtain

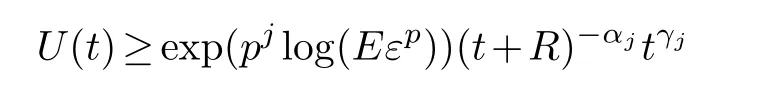
The proof is completed.

Acknowledgements

The authors express their heartfelt thanks to the editors and referees who have provided some important suggestions.