Full Friendly Index Sets of a Family of Cubic Graphs

( School of Mathematics and Information Science, Henan Polytechnic University,Jiaozuo 454003, China)

Abstract: Let G=(V,E) be a graph.For a vertex labeling f:V →Z2, it induces an edge labeling f+:E →Z2, where for each edge v1v2 ∈E we have f+(v1v2)=f(v1)+f(v2).For each i∈Z2,we use vf(i)(respectively,ef(i))to denote the number of vertices(respectively,edges) with label i.A vertex labeling f of G is said to be friendly if vertices with different labels differ in size by at most one.The full friendly index set of a graph G, denoted by FFI(G), consists of all possible values of ef(1)-ef(0), where f ranges over all friendly labelings of G.In this paper, motivated by a problem raised by [6], we study the full friendly index sets of a family of cubic graphs.

Keywords: Vertex labeling; Friendly labeling; Embedding labeling graph method; Cubic graph

§1.Introduction

Many real-world situations can be modeled by a graph consisting of a set of vertices together with edges joining certain pairs of these vertices.Especially, labeling graphs often paly a vital role in applications such as: parallel computing, circuit design, coding theory, communication network addressing, data base management, secret sharing schemes, see [1,2,15,20–22,24]and their references.

LetG=(V(G),E(G)) be a connected simple graph.Avertex 0-1 labeling f:V(G)→Z2induces anedge 0-1 labeling f+:E(G)→Z2, given by

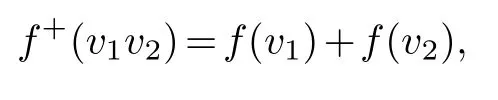
for eachv1v2∈E(G).

For eachi∈Z2, a vertexuis called ani-vertexiff(u)=i, and an edge is called ani-edgeiff+(e)=i.An edge is also called an (i,j)-edgeif it is incident with both ani-vertex and aj-vertex.Define

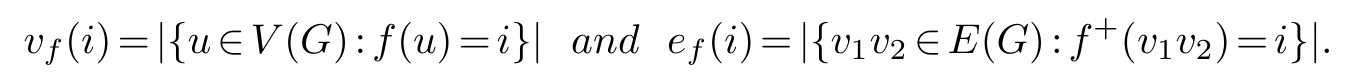
A vertex labelingfof a graphGis said to befriendlyif

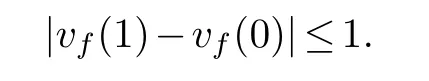
A graphGwith a friendly labelingfsuch thatef(1)-ef(0)=k, denoted byGf(k), is called alabeling graph with friendly index k.Throughout this paper, we usually drop the subscriptfif this is unambiguous.

Thefull friendly index set, introduced by Shiu and Kwong [17], is the set

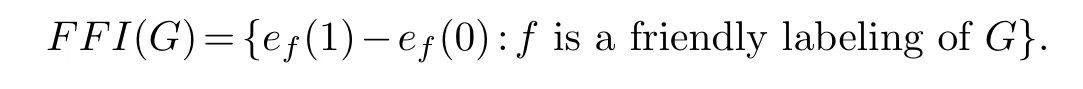
A friendly labeling of a graphGwas also known as a bisection ofG, which has been studied extensively in the area of graph partitions [4,5,7–9,12,14,23].From the algorithm perspective,it is NP-hard to find the maximum or minimum bisection (namely, friendly labelings with maximum or minimum 1-edges) of an arbitrary graph.Researchers usually focus their studies on some specific graphs.For example, Lee and Ng [13]determined the friendly index sets of cycles, complete graphs and some bipartite graphs.Kwong and Lee [10]determined the friendly index sets of 2-regular graphs.Recently, Gao et.al.[6]obtained the full friendly index sets of a family of cubic graphs, which are full vertices blow-up ofCmbyK1,1,2.The answers for the full friendly index sets of general cubic graphs are still unknown.

Definition 1.1.Let G=(V,E)and H=(V1,E1)be two graphs.Suppose u∈V(G)is a d-degree vertex and u1,...,ud are its neighborhoods.Let v1,...,vd be d distinct vertices of H.We say u is blow-up by H at vertex v1,...,vd if we delete u and joint ui to vi for1≤i≤d.The full vertices blow-up graph G(H)is obtained by blowing up each vertex of G by a copy of H.

Definition 1.2.Let G1and G2be two labeling graphs, e=u1u2∈E(G1)is an(a,b)-edge and the labels of v1,v2∈V(G2)are c, d, respectively.A new labeling graph G(e,{v1,v2}), calledembeddingG2onG1ate, is obtained by

(1) Subdivide e by inserting a new vertex u on it,

(2) Blow-up u by G2at v1,v2.

Suppose vi is jointed to ui for i∈[2].Let k be the friendly index of G1, the embedding operation is denoted by a+c+(k)+d+b.

In [6], the authors posed the following problem.

Problem[6]For what type of cubic graphs, their full friendly index sets can be obtained by embedding labeling graph method?

Letbe the bipartite graph obtained by deleting an edge fromK3,3, and letv1,v2to be the two 2-degree vertices insee Figure 1.LetCmbe a cycle of lengthm.Denote byCm() the full vertices blow-up ofCmbyatv1,v2, see Figure 2.Clearly,Cm() is a cubic graph with order 6mand size 9m.In this paper it is simplified using the embedding labeling graph method and then extended to handle the full friendly index set ofCm().

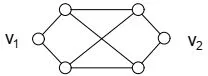
Fig.1 Graph

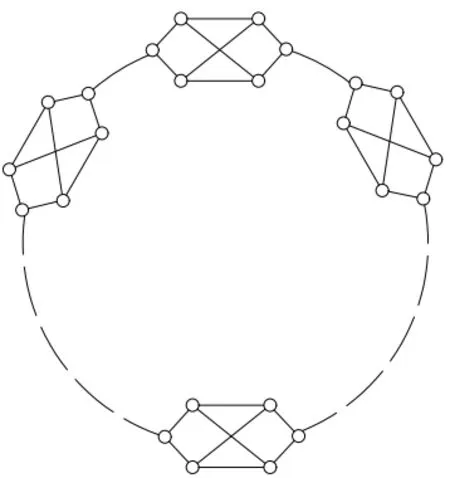
Fig.2 Graph Cm()

§2.Preliminaries

We give some results on labeling of graphs, note that in the first two the labelings is not necessarily friendly.

Lemma 2.1.[19]Let f be a labeling of a graph G that contains a cycle C as its subgraph.If C contains a1-edge, then the number of1-edges in C is a positive even number.

Lemma 2.2.In all possible(0,1)-labelings of the vertices of , we have e(1)-e(0)equals-8, -4, -2,0,2,4, or8.

Proof.In any (0,1)-labeling of, sincee(1)+e(0)=8, we have

In our figures of labeling graphs, vertices marked·are labeled 1 and vertices marked◦are labeled 0.

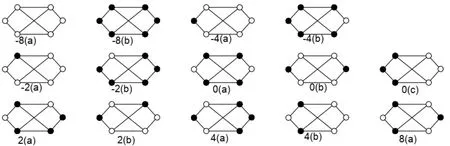
Fig.3 All possible (0,1)-labelings of

Now we consider friendly labelings and give our key lemma.

Lemma 2.3.Let G be a cubic graph.In any friendly labeling of G, if two vertex labels are exchanged, then e(1)changes by -6, -4, -2,0,2,4, or6.

Proof.When exchanging the labels of two verticesu, vin a labeling cubic graphG, the edge labels will not change for edges which contain neitherunorv.Therefore, we shall only consider edges which contain eitheruorv.Now exchange the labels ofuandvand denote the new labeling byf′.Iff(u)=f(v), thene(1) changes by 0.Supposef(u)≠f(v), we divide the proof into three cases according to the distanced(u,v) ofu,v(namely, the length of the shortestu,v-path inG).

Case (a),d(u,v)≥3.Note thatef(1)+ef(0)=6, whereef(1)∈{0,1,2,3,4,5,6}under labelingf.Inf′, all of the six edges are changed their labels (from 0 to 1 or from 1 to 0).Soef′(1)=ef(0)=6-ef(1) and the number of 1-edges changed by

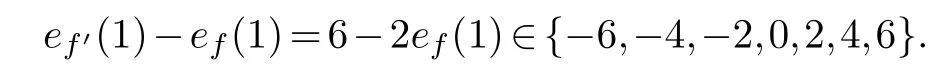
Case(b),d(u,v)=2.Regardless of the label ofv1inf,there always havef(uv1)=1-f(vv1).This impliesef(1)≠0,6.Among the remainder four edges, supposexof them are labeled 0 inf′, wherex∈{0,1,2,3,4}.Then

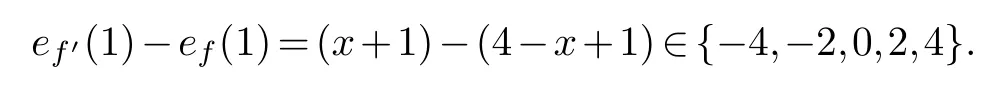
Case(c),d(u,v)=1.Note thatf′(uv)=f(uv)=1.Among the remainder four edges,supposexof them are labeled 0 inf′, wherex∈{0,1,2,3,4}.Then

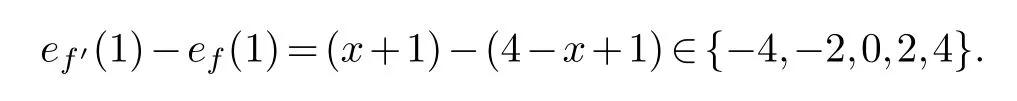
This completes the proof.

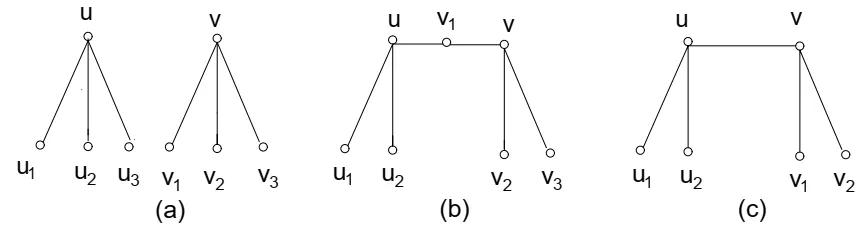
Fig.4 Three possible structures of two vertices in a cubic graph

§3.The full friendly index sets of Cm()

In this section,we obtain the full friendly index sets ofCm()by a sequence of embedding process.We only do embedding at cycle edges.For example, inC2(-14) we embed 0(c) of Figure 3 at some (0,1)-cycle-edge thenC3(-17) is obtained (see Figure 8).We divide our proof into two cases according to the parity ofm.

3.1. m is even

Firstly, we give the maximum and minimum value ofFFI(Cm()).

Lemma 3.1.When m is even, we have

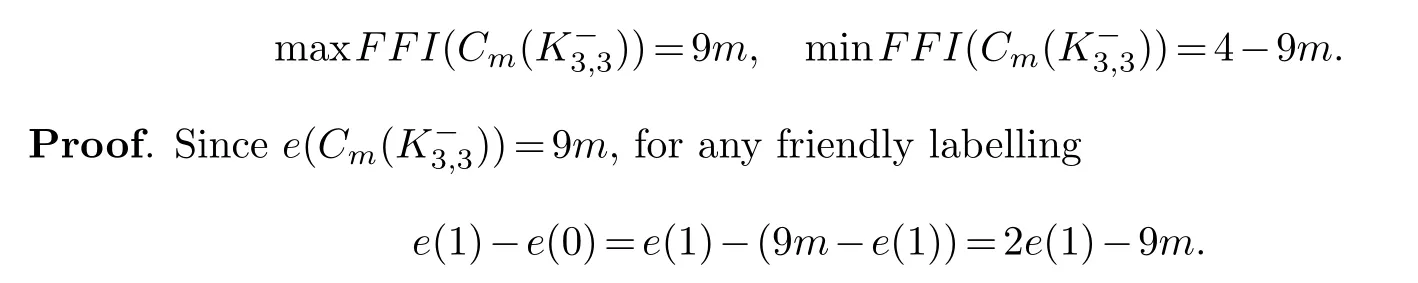
We show that maxe(1)=9mand mine(1)=2, then the result follows immediately.

Considering the full vertex blow-up ofCmby 8(a), vertex labeled 0 is jointed to vertex labeled 1 in each blow-up operation.(See the bottom right labeling graph in Figure 5 for the casem=2.) This implies maxe(1)=9m.

SinceCm() is connected, at least one 0-vertex is adjacent to a 1-vertex, we seee(1)＞0.Note that each edge ofCm() is lying on a cycle.By Lemma 2.1, we know thate(1)≥2.Through blowing upm/2 consecutive vertices ofCmby-8(a) and blow up others by-8(b),then joint the 2-degree vertices successively.(See the upper left labeling graph in Figure 5 for the casem=2.) This implies mine(1)=2.

The proof of our main result is by using induction, we show them=2 andm=4 cases first.

Lemma 3.2.FFI(C2())={4i+2:-4≤i≤4}.

Proof.From Lemma 3.1, for any friendly labelling

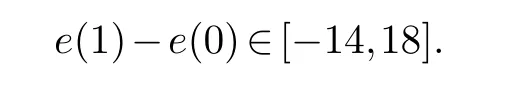
If we change the labels of two vertices, then by Lemma 2.3 the value ofe(1) changes is even.Hence, each possible friendly index is 2 (mod 4) from-14 to 18, see Figure 5.

Fig.5 Labeling graphs G2(4i+2) (-4≤i≤4)

Lemma 3.3.FFI(C4())={4i:-8≤i≤9}.

Proof.From Lemma 3.1, for any friendly labelling

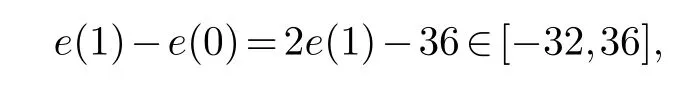
and by Lemma 2.3 each possible index is 0 (mod 4) from-32 to 36.Therefore,

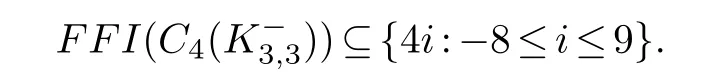
Now we use the embedding labeling graph method to show the reverse direction.

InG2(-10) andG2(14) do

InG2(4i+2) (-2≤i≤2),G2(-14) andG2(18) do

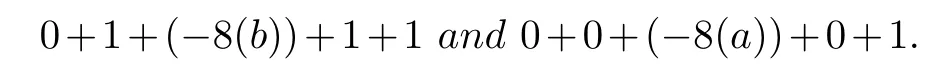
Compared withG2(4i+2) (-4≤i≤4), the valuee(1)-e(0) is decreased by 18.So we obtainG4(4i) (-8≤i≤0) and denote them byA.

InG2(-10) andG2(14) do

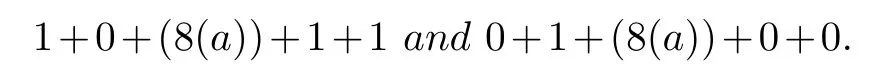
InG2(4i+2) (-2≤i≤2),G2(-14) andG2(18) do

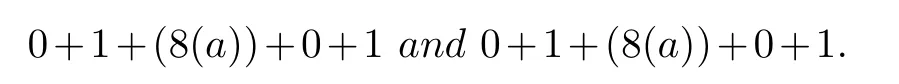
The valuee(1)-e(0) is increased by 18, we obtainG4(4i) (1≤i≤9) and denote them byB.

CombiningAandBwe have the desired conclusion.The labeling graphsG4(4i)(-8≤i≤9)are illustrated in Figure 6.

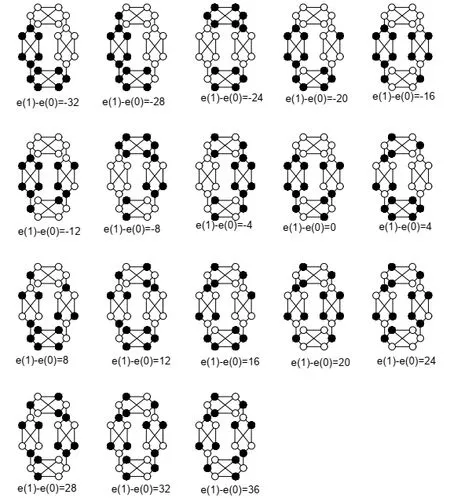
Fig.6 Labeling graphs G4(4i) (-8≤i≤9)

In order to getCm+2(K1,1,2), the authors [6]embed two labelingK1,1,2on two cycle-edges ofCm(K1,1,2).In this paper, we simplified the embedding operation by embedding twoonce a time.Considering the labeling graphs-15(a) and 17(a) in Figure 7.Note that both labelings in the depictured graphs are friendly.Hence, if the labeling ofCm() is friendly,then so doesCm+2().

Fig.7 -15(a) and 17(a)

Theorem 3.1.When m≥2is even,

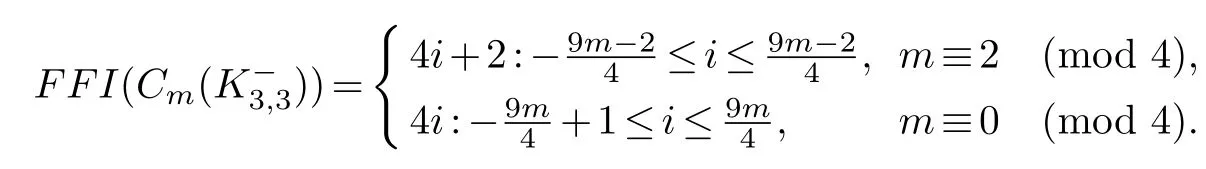
Proof.By Lemma 2.3 and Lemma 3.1, the left hand is a subset of the right.We prove the opposite direction by induction onm.By Lemma 3.2 and Lemma 3.3, the theorem is true form=2,4.Suppose that it holds form=n(≥6).It should be noticed that in the following we will do the embeddings on some 1-edges or 0-edges, so one should carefully examine the existence of such edges.

3.2. m is odd

Lemma 3.4.When m is odd, we have

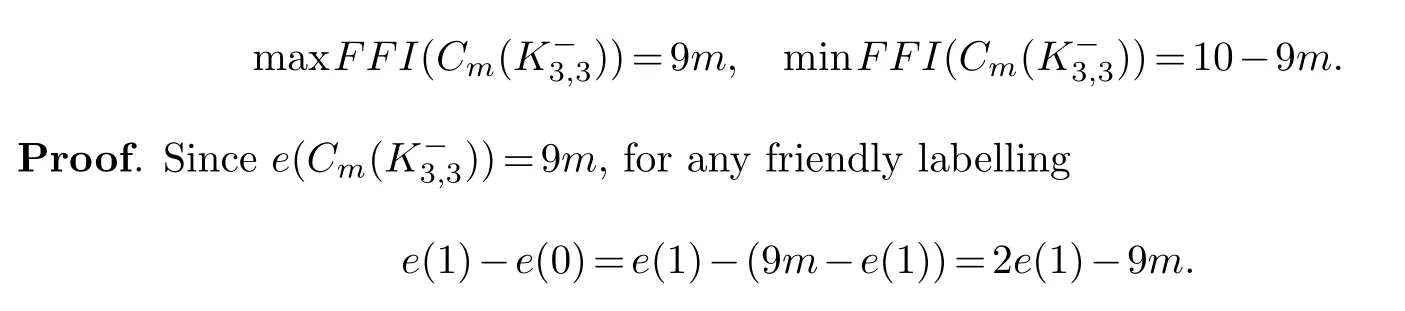
We show that maxe(1)=9mand mine(1)=5, then the result follows immediately.

Considering the full vertex blow-up ofCmby 8(a), vertex labeled 0 is jointed to vertex labeled 1 in each blow-up operation.(See the bottom right labeling graph in Figure 8 for the casem=3.) This implies maxe(1)=9m.

SinceCm() is connected, at least one 0-vertex is adjacent to a 1-vertex, which impliese(1)＞0.Note that every edge ofCm() lies on a cycle.

By Lemma 2.1, we know thate(1)≥2.Through blowing upconsecutive vertices ofCmby-8(a) andconsecutive vertices by-8(b), then joint the 2-degree vertices successively.Sincemis odd, so in one-subgraph, three vertices are labeled 0 and the others are labeled 1.

Hence, there are at least four edges are labeled 1 in this-subgraph.(See the upper left labeling graph in Figure 8 for the casem=3.) This implies mine(1)=5.

The proof of our main result is by using induction, we show them=3 andm=5 cases first.

Lemma 3.5.FFI(C3())={4i+3:-5≤i≤6}.

Proof.From Lemma 3.4, for any friendly labellinge(1)-e(0)∈[-17,27].If we change the labels of two vertices, then by Lemma 2.3 the value ofe(1) changes is even.Hence, each possible index is 3 (mod 4) from-17 to 27, see Figure 8.

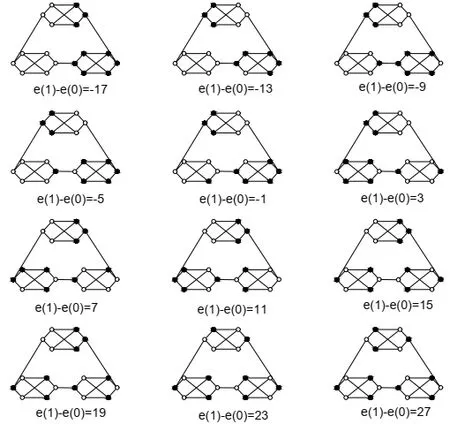
Fig.8 Labeling graphs G3(4i+3) (-5≤i≤6)

Lemma 3.6.FFI(C5())={4i+1:-9≤i≤11}.

Proof.From Lemma 3.4, for any friendly labelling

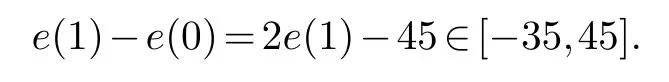
By Lemma 2.3, each possible index is 1 (mod 4) from-35 to 45.Therefore,FFI(C5())⊆{4i+1:-9≤i≤11}.

Now we use the embedding labeling graph method to show the reverse direction.InG3(4i+3) (-5≤i≤6), there exist at least one 1-edge in every labeling graph.

InG3(4i+3)(-5≤i≤6),do 0+0+(-15(a))+0+1.Compared withG3(4i+3)(-5≤i≤6),the valuee(1)-e(0) is decreased by 18.We obtainG5(4i+1) (-9≤i≤2) and denote them byC.

InG3(4i+3) (-2≤i≤6), do 0+0+(17(a))+0+1.The valuee(1)-e(0) is increased by 18, we obtainG5(4i+1) (3≤i≤11) and denote them byD.

CombiningCandDwe have the desired conclusion.The labeling graphsG5(4i+3)(-9≤i≤11) are illustrated in Figure 9.

Fig.9 Labeling graphs G5(4i+1) (-9≤i≤11)

Theorem 3.2.When m≥3is odd,

Proof.By Lemma 2.3 and Lemma 3.4, the left hand is a subset of the right.We prove the opposite direction by induction onm.By Lemma 3.5 and Lemma 3.6, the theorem is true form=3,5.Suppose that it holds form=n(≥7).It should be noticed that there exists a 1-edge inGn(4i+3).

§4.Other related labeling indices

In this section, we would like to mention some other kinds of indices about friendly labeling of graphs.The first one isfriendly index set FI(G) which was introduced in [3], it is the set of absolute values of all numbers inFFI(G).More formally,

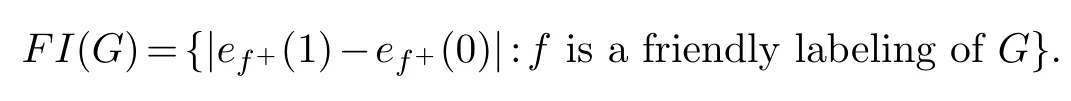
By Theorem 3.1 and Theorem 3.2, we obtain

Corollary 4.1.For odd m≥1,

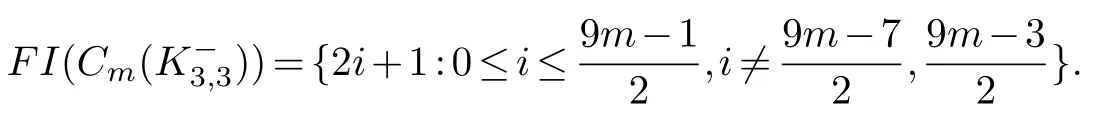
For even m,

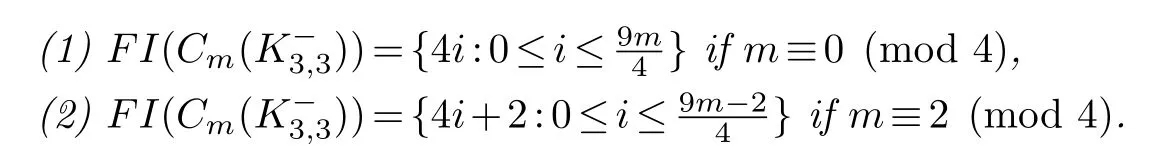
A graphGiscordialif-1, 0, or 1∈FFI(G), see [3,16].The cordiality ofCm() follows immediately form our main results.

Corollary 4.2.For odd m≥1, the graph Cm()is cordial.For even m≥2,

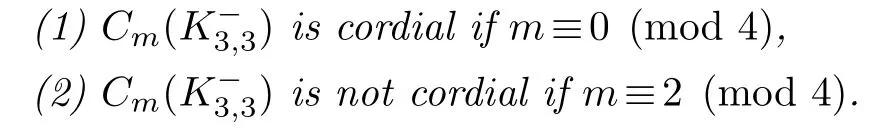
Shiu and Kwong [18]introduced the full product-cordial index set of graphs.LetG=(V,E)be a graph.A vertex friendly labelingf:V →Z2induces an edge labelingf*:E →Z2, given byf*(xy)=f(x)f(y) for eachxy ∈E.For eachi∈Z2, letvf(i)=|{u∈V(G):f(u)=i}|andef*(i)=|{xy ∈E(G):f*(xy)=i}|.Thefull product-cordial index setofG,denoted byFPCI(G),is defined as

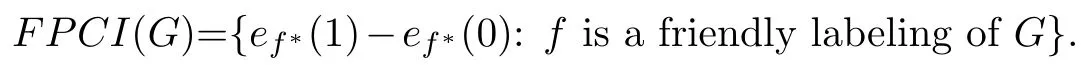
Lemma 4.1.Let G be a d-regular graph and let f:V(G)→Z2be a friendly labeling of G.For i∈Z2, denote Vi=f-1(i)and e(Vi)=e(G[Vi]).Then

Proof.Lete(V0,V1) be the number of edges with one end inV0and the other inV1.Without loss of generality, suppose|V0|≥|V1|.The result follows by simply considering the sum of degrees of vertices inV0andV1:

This completes the proof.

Ifdis odd, then the ordern(G) of anyd-regular graphGmust be even by the handshaking principle.So we always havee(V0)=e(V1) in any friendly labeling ofG.Now we consider the edge labelingf*defined above, we obtainef*(1)=e(V1) andef*(0)=e(V0)+e(V0,V1).Therefore, we obtain the following relationship between friendly index set and product-cordial index ofd-regular graphs whendis odd

In [11], the authors also ask for connections between friendly index set and product-cordial index set of general simple graphs.By Theorem 3.1 and Theorem 3.2, we have

Corollary 4.3.The full product-cordial index sets of Cm(K-3,3)is