基于NMF算法的多标记学习
2021-10-13李闪闪田文泉潘正高
李闪闪,田文泉,潘正高
(宿州学院 信息工程学院,安徽 宿州 234000)
大数据时代,信息的高速产生和发展,使得从海量、庞大的“大数据”信息中筛选和挖掘出有价值的数据信息成为了新的技术挑战.现实世界中事物的存在往往面临多义性问题,即一个样本可能不仅仅具备一个标记信息,这种情况下,多标记学习[1]的框架应运而生.在该框架下,为了更好地描述数据对象,需要收集丰富的特征数据.与此同时,特征数据的大量增长也会伴随许多冗余特征的产生,从而造成分类困难,增加模型的训练时间.因此,对多标记数据的维度约简处理有重要意义.
矩阵分解技术是一种常见的对复杂、高维度数据进行压缩、去噪和降维的方法.传统的矩阵分解是将一个维数较大的矩阵分解成V=WH的形式,而不在乎分解后的矩阵W和H中元素是正值还是负值.但是实际生活中,矩阵中负值元素不具备物理可解释意义.比如,在图像处理中,每一个非负数值都可以被解释为与之对应的特征图例.在文本统计中,每一个非负取值都可以表示一篇文章的主题.而如果这些元素为负值,就无从解释了.
为了解决这一问题,Lee和Seung在《Nature》提出了一种有限定约束条件的非负矩阵分解(Non-negative Matrix Factorization,NMF)算法[1].该算法限定矩阵中所有元素均为非负值,规避了传统的矩阵分解技术中存在可解释性比较差的问题.NMF算法通过非负分解数据矩阵,将原始矩阵维数进行削减、压缩,是处理大规模数据的一种有效手段.基于此,针对高维数据在多标记学习中带来的分类困难等问题,本文提出一种基于NMF算法的多标记学习技术(A Multi-label Learning Method Based on NMF Algorithm,ML-NMF).首先,针对大规模的多标记数据集,本文采用NMF算法对其进行特征降维.其次,融合标记空间,训练ELM极限学习机[2]模型,最后,将该模型下对未知标记的分类预测结果与其他常见的多标记特征降维方法进行对比,结果显示本文算法是有效的.
1 NMF算法
1.1 NMF算法原理
已知有m个n维向量的数据矩阵X={x1,x2,…,xm},NMF算法[3]的本质是把原始数据矩阵X用两个非负矩阵W={w1,w2,…,wr}和H={h1,h2,…,hm}的乘积来近似表示,即:
Xn×m≈Wn×r·Hr×m,
(1)
其中,W被称作基本矩阵,H被称作系数矩阵,并且r远小于n和m,这样用H代替原始数据矩阵X便可以达到对原始矩阵X进行数据压缩与降维处理的目的.
1.2 NMF算法求解
NMF算法[4]基本原则是将原高维空间的数据矩阵X投影到低维度的线性空间,用低维的矩阵H表示,因此,NMF算法本质是最小化原矩阵X与分解矩阵W和H的差异度,即转化为公式(2)的优化问题:
minf(W,H)
s.t.0≤W∈Rn×r,0≤H∈Rr×m,
(2)
其中f(W,H)是差异度函数,借助于Euclidean距离作为评判标准求得该公式的局部最优解[5].算法具体步骤如下.
算法:基于Euclidean距离的非负矩阵分解;
输入:数据特征矩阵X,迭代次数t;
输出:非负分解矩阵W和H.
(1)随机初始化非负矩阵W和H.
(2)对迭代次数t=1,2,…

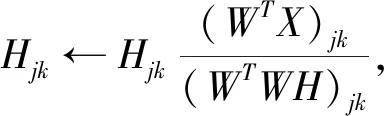
(3) 输出非负分解矩阵W和H.
2 多标记学习
2.1 问题定义
在多标签学习中X表示标签特征,X=Rp表示定义在实数域R上的p维样本空间,Y={y1,y2,…,yq}表示标记空间.给定多标记数据集D={(xi,Yi)|1≤i≤n},其中每一个xi=[xi1,xi2,…,xip]表示数据集的第i个样本,该样本含有p个特征,而Yi=(yi1,yi2,…,yiq)表示与每个样本xi对应的一组标记序列,并且满足,Yi∈{-1,+1},如果样本xi包含第k个标记,则yik=+1,否则yik=-1.多标记学习主要是通过训练数据集D,获得从原始输入空间X到最终输出空间的一个映射模型f:X→2Y.该模型满足:当输入待分类样本xi∈X时,通过分类器f能够预测得到属于该样本的类别标记集合f(x)⊆Y.
2.2 多标记学习评价指标
由于多标记数据结构的复杂性,传统的单标记学习评价标准已经不能准确评判算法的好坏.因此,针对多标签数据的评估指标被提出,其中常用的有平均查准率(Average Precision,AP)、覆盖率(Coverage,CO)、汉明损失(Hamming Loss,HL)、一错误率(One-Error,OE)、排位损失(Ranking Loss,RL)[1]等,设有预测函数f(x,y)定义排序函数为rankf(x,y),若给定多标记测试集S={(xi,yi)|1≤i≤P},具体描述如下:
平均查准率(Average Precision, AP)用于评估在样本的预测标记序列中,排在前面的标记同时也是真实标记的情况.该指标值越大,分类效果越好,公式定义如下[1]:
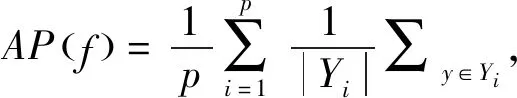
(3)
覆盖率(Coverage,CO)用于评估在样本的预测标记序列中,找出全部样本所含的标记类别至少需要多少个标记.该指标值越小,分类效果越好,公式定义如下[1]:
(4)
汉明损失(Hamming Loss,HL)用于评估预测标签集合和实际标签集合之间的差距情况.该指标值越小,分类效果越好,公式定义如下[1]:
(5)
排位损失(Ranking Loss,RL)用于评估无关标记的排在真实标记之前的比例情况.该指标值越小,算法性能越好,公式描述如下[1]:

(6)
一错误率(One-Error,OE)用于评估在样本的预测标记排序中,排在前面单但是不属于样本的真实标记的情况.该指标值越小,分类效果越好,公式定义如下[1]:

(7)
3 基于NMF算法的多标记学习
3.1 数据形式化表示
假定现有X=Rp代表p维样本空间,Y={y1,y2,…,yq}表示标记空间.对于给定的多标记数据集D={(xi,Yi)|1≤i≤n},其中xi=(xi1,xi2,…,xip)表示的是数据集中第i个样本,并且每个样本包含p个特征,而Yi=(yi1,yi2,…,yiq)表示与每个样本xi对应的一组标记序列.基于此,本文实验训练数据集的特征矩阵和标签矩阵分别描述为X=(x1,x2,…xn)T∈Rn×p和Y=(Y1,Y2,…Yn)T∈{+1,-1}n×q.
3.2 ML-NMF算法分析
本文利用非负矩阵分解算法能够进行数据降维的特性,对于海量的多标记数据集进行处理,提出一种基于非负矩阵分解的多标记学习算法(ML-NMF).基本思路是:①输入原始数据特征矩阵和标记矩阵相关信息,设置好相应参数以及需要选择的特征数量;②使用NMF分解算法进行降维处理,获取特征排序序列;③借助于ELM极限学习机进行特征映射,建立特征与标记的训练模型.
ML-NMF算法的具体实现步骤如下.
算法:基于NMF算法的多标记学习;
输入:原始数据特征矩阵X,标记矩阵Y,降维后的特征个数k;
输出:降维的特征索引向量I.
(1) 随机初始化特征空间矩阵X;
(2) 利用优化公式迭代求解满足条件的非负矩阵X′;
(3) 利用非负矩阵结构获得特征排序的前k个特征;
(4) 输出降维的特征索引向量I.
4 实验及结果分析
4.1 实验数据
为了分析算法的实验性能,本文实验共计选取6个公开基准多标记数据集:Birds、Emotion、Flags、Natural Scene、Scene和Recreation,数据集信息如表1所列.
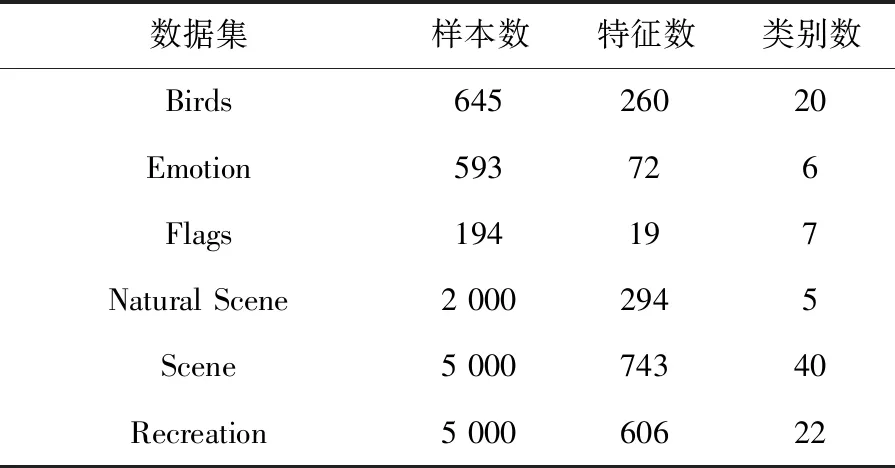
表1 多标记数据集
所选数据集均是取自http://mulan.sourceforge.net/datasets.html.
4.2 实验环境与实验对比方案
实验代码均在Windows 10 、Matlab2016a 中运行,硬件环境为Intel i5-4200 CPU 8G 内存.为了分析算法的实验性能,选择5种典型评价指标,分别是:平均查准率(AP)、汉明损失(HL)、覆盖率(CV)、一错误率(OE)和排位损失(RL)作为算法的性能评价指标.通过这5种评价指标来共同评价ML-KNN[6]、Rank-SVM[7]、ML-RBF[8]和ML-NMF 4种算法的性能,最终得出各算法的整体效能评估结果.如表2~6所列,用黑体突出标识,作为此实验结果的最优数值,采用统计分析的方法对各种算法进行排序.
4.3 实验结果与稳定性分析
表2~6分别给出在Birds、Emotion、Flags、Natural Scene、Scene和Recreation数据集上的算法实验结果.各评价指标之后的向上“↑”代表值越大,实验性能越优;向下“↓”则代表值越小,实验性能越优.
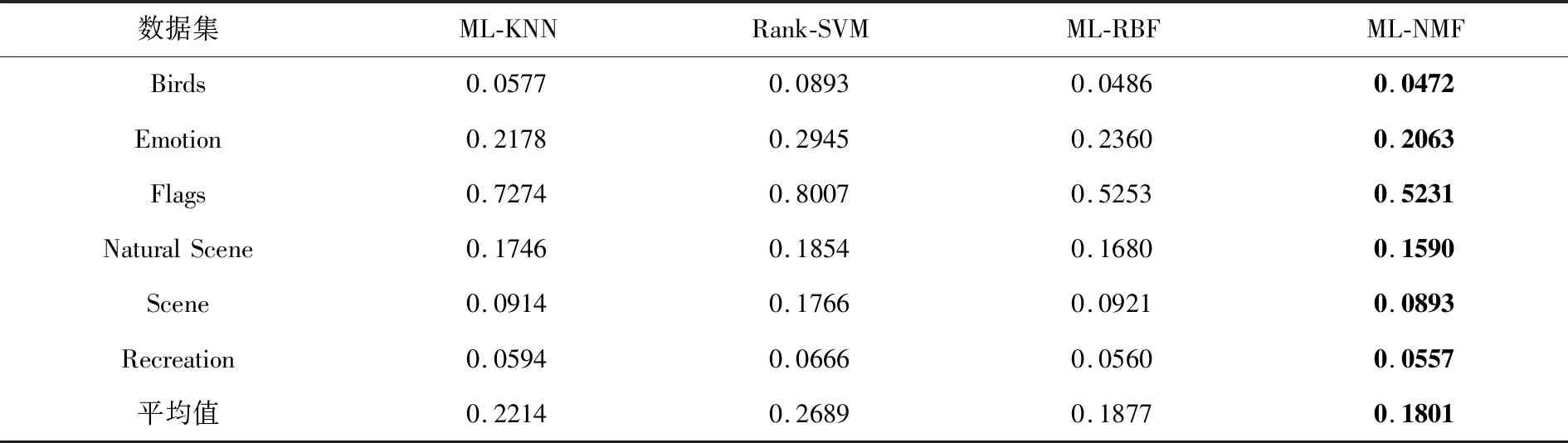
表2 汉明损失测试结果
表2基于汉明损失(HL)的评价结果显示,本文提出的ML-NMF算法在6个数据集上的实验结果均优于其他3种算法;表3基于排位损失(RL)的评价指标可以看出NL-NMF算法也明显优于其他3种算法;表4基于一错误率(OE)的评价指标显示,仅仅在Flags一个数据集上结果低于ML-RBF算法,但整体结果较优;表5基于覆盖率(CV)的评价指标,Rank-SVM也仅仅在Recreation这一个数据集上表现较好,其余数据集实验结果均不及本文的ML-NMF算法;表6基于平均查准率(AP)的整体实验结果也是优于其他3种算法.总体分析,本文提出的ML-NMF算法在各个数据集实验结果都要胜于其他算法,因此,本文提出的基于NMF的多标记学习是可行的.

表4 一错误率测试结果
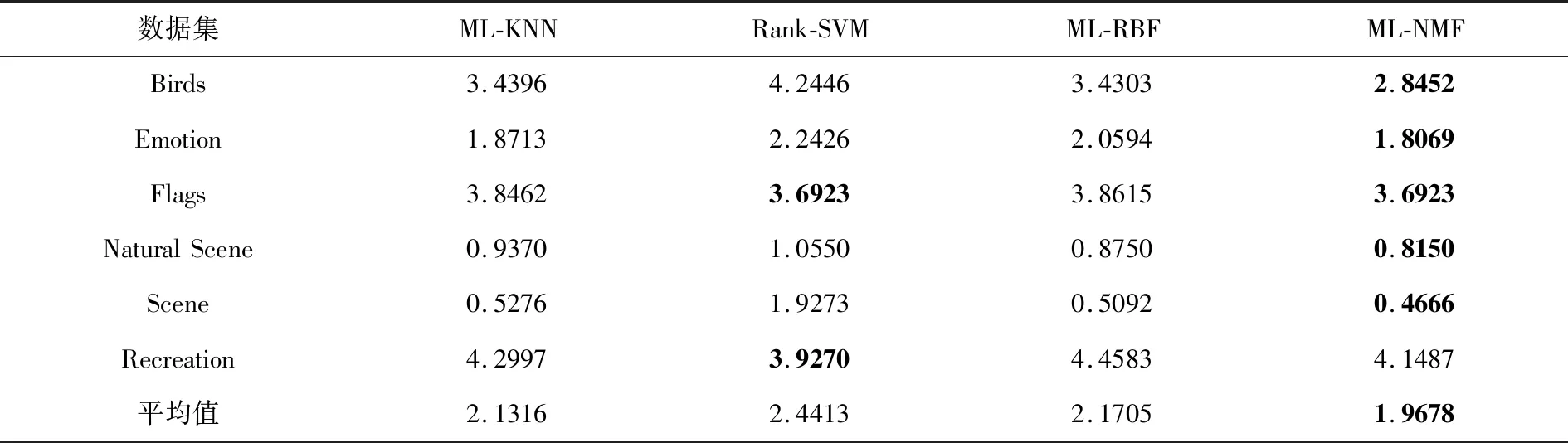
表5 覆盖率测试结果
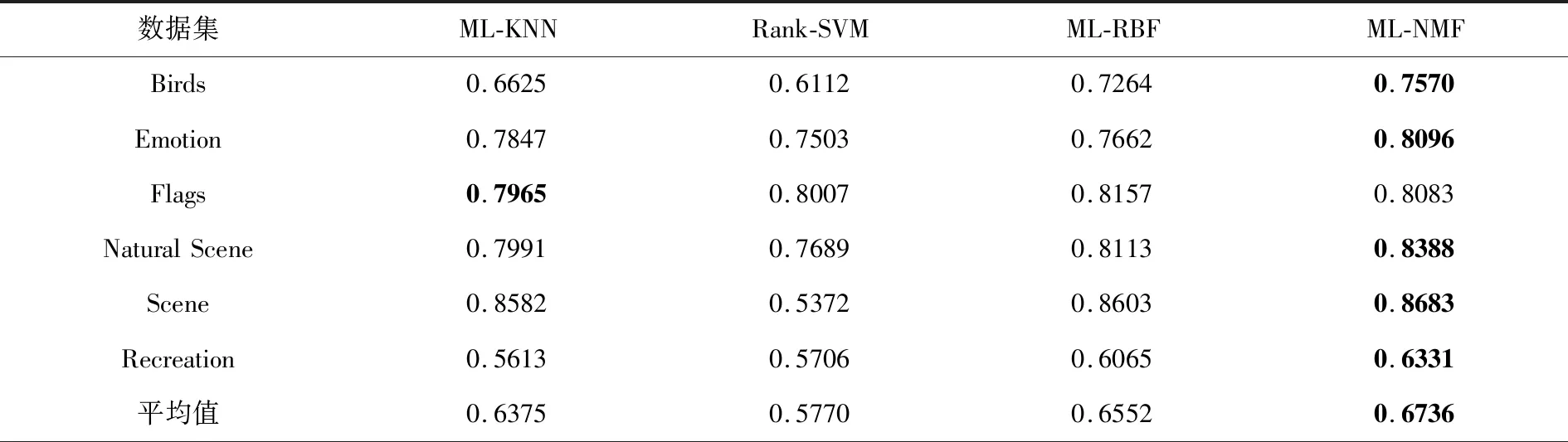
表6 平均查准率测试结果
5 结语
本文介绍的基于NMF算法的多标记学习,首先采用NMF算法对标记数据集进行维度约简,然后将约简后的特征子集融合标记信息,训练分类模型,预测未知标记.最终基于5种相同评价指标,在6种数据集上的实验结果表明,本文提出的ML-NMF算法具有很好的分类效果.
