非局部边界条件下的反应扩散方程的爆破解
2021-10-13岳丽霞
岳丽霞
(兰州交通大学 数理学院,甘肃 兰州 730070)
0 引言
偏微分方程理论是以建立数学模型的方式分析和解决物理学、化学、生态学等领域中存在的实际问题,反应扩散方程作为偏微分方程的重要分支之一,其爆破解可以恰当地描述很多自然现象,例如医学、生物学和传染病领域中物质的不稳定性扩散等.因此,对反应扩散方程爆破解的研究具有一定的实际意义.
近年来,以Laplace算子(Δu)作为扩散项的反应扩散方程爆破解问题的研究已取得了很多重要成果[1-6].王玉兰等[1]利用上下解方法,研究了Dirichlet非局部边界条件下具有阻尼项的反应扩散方程全局解存在和不存在的条件,并对爆破解的速率做了估计.Monica Marras等[2]利用微分不等式技巧,得到了非局部边界条件下具有时间加权的反应扩散方程发生爆破的条件,以及当爆破发生时爆破时间的上下界.杨慧等[3]研究了具有非局部非线性Neumann边界条件和非线性吸收项的非局部反应扩散方程解的性质,通过构造适当的上下解方法,给出了正解全局与非全局存在性的充分条件.刘丙辰等[4]利用上下解方法研究了在Neumann非局部边界条件下具有的非线性非局部源的反应扩散方程的爆破现象,得到了该问题解全局存在的条件以及一维空间中的爆破率和高维空间中爆破时间的上下界.L E PAYNE等[5]利用微分不等式技巧证明了具有Neumann齐次边界条件的反应扩散方程解的存在性,并获得了解发生爆破的条件.马羚未等[6]利用微分不等式技巧和上下解方法分别得到了Dirichlet边界条件下具有加权梯度反应项问题爆破时间的上下界.
受文献[5]和[6]启发,本文将研究非局部边界条件下非线性反应扩散方程:
(1)
解的性质.
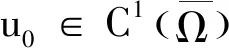
(a1)a(x)>0,x∈Ω且a(x)=0,x∈∂Ω.
(a3)-a(x)A≤∇a(x)≤a(x)A⟺
其中,A=(A1,A2,…,AN)是一个正向量.
由于边界条件不同,文献[6]的辅助函数不再适用于问题(1),因此,需要构造新的辅助函数来研究问题(1).本文通过构造适当的辅助函数,利用微分不等式技巧分别得到了爆破时间的上界和下界.通过本文和文献[6]的比较,发现边界条件对解的存在性与爆破性有着显著影响.
1 解的存在性
定理1假设非负函数f和g满足以下条件:
f(|∇ε|)≤-εp,ε≥0,
(2)
(3)
其中p>1,q>1,且满足:
2q (4) 那么,问题(1)的解u(x,t)不会发生爆破,即对于所有的t>0,解存在. 证明令 (5) 由(1)和(2)可得 (6) 由格林公式及(3)得 (7) 对恒等式 ∇(uq+1x)=Nuq+1+(q+1)uq(x·∇u) 在Ω上积分,可得 (8) (9) 根据几何平均不等式可得 (10) 取 (11) 故 (12) 由(9)和(12)得 (13) (14) 其中 (15) 根据(14),对于任意的μ>0,有 (16) 把(16)代入(13),有 (17) 其中 (18) 利用Holder不等式得 即 (19) 取μ充分小,并由(16)、(17)及(19)可得 (20) 其中 由Holder不等式得 (21) 因而(20)可化为 (22) 由(22)可得出结论,当 (23) 在时间区间上φ(t)是递减的.因此,在定理1所述的条件下,φ(t)始终保持有界. 定理2设u是问题(1)的一个解,假设下列条件成立: (24) 其中 (25) 假设ψ(0)≥0,且有 (26) 那么,问题(1)的解在t* (27) 如果β=0,则有T=∞. 证明首先对φ(t)求导,并利用格林公式,有 (28) 对ψ(t)求导有 (29) (30) 由(29)、(30)得 (31) 因为ψ(0)>0,所以∀t∈(0,t*),有ψ(t)>0. 由Schwarz不等式有 (32) 由(28)和(32)得 (33) 从而 (ψφ-(1+β))′≥0. (34) 对上式从0到t积分,得 ψ(t)(φ(t))-(1+β)≥ (35) 于是(28)可化为 φ′(t)≥2(1+β)ψ(t)≥2(1+β)Mφ1+β. (36) 再次积分得 (φ(t))-β≤(φ(0))-β-2β(1+β)Mt. (37) 显然,(37)不会一直成立,且对于β>0有 (38) 特别地,如果β=0,由(36),对于t>0有 φ(t)≥φ(0)e2Mt. (39) 显然,t*=∞,即在适当的时间解发生爆破,证毕. 定理3假设u(x,t)是问题(1)的一个解,非负可积函数f,g满足: f(s)≥sp,g(s)≥sq,s≥0, (40) q>p>1. (41) (42) 其中 证明首先,对φ(t)求导,利用(40)、(41)以及格林公式,可得 (43) 由Holder不等式得 (44) 根据Poincare不等式得 (45) (46) 将(45)和(46)代入(44)并结合Holder不等式,可得 (47) 其中 对(47)从0到t*积分,可得 定理3证毕. 定理4假设u(x,t)是问题(1)的一个解,f,g满足: (48) (49) 证明定义如下形式的辅助函数: (50) 对Γ(t)关于t求导并由(48)可得 (51) 由文献[2]得 (52) 由Young不等式得 (53) 把(53)代入(52)得 (54) 其中 由Poincare不等式 (55) 使得(51)成立.把(54)、(55)代入(51),并结合Holder不等式得 (56) 其中 (57) 则 定理4得证. 在研究反应扩散方程解的爆破问题时, 本文采用了构造辅助函数和微分不等式技巧相结合的方法, 得到了问题(1)的整体解和爆破解的存在性定理. 对比文献[6], 由于边界条件的不同, 需要构造新的辅助函数来研究爆破时间的上下界. 本文得到了两个测度函数下爆破时间的不同上界以及一个下界. 通过与文献[6]的比较发现: 边界条件对解的存在性和爆破性有显著影响; 辅助函数不同, 爆破时间的上下界不同.
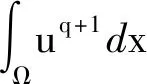
2 爆破

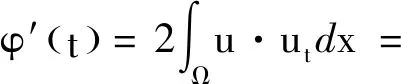
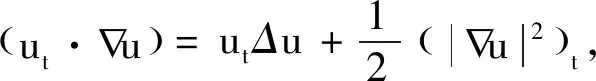
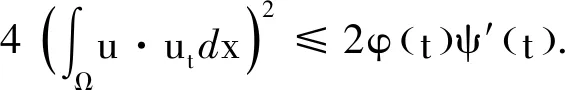
ψ(0)(φ(0))-(1+β)=M.3 爆破时间的上界
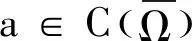
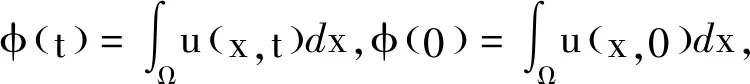


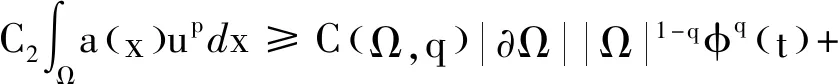

4 爆破时间的下界

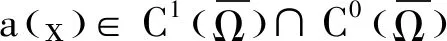
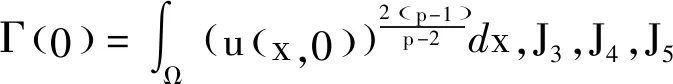
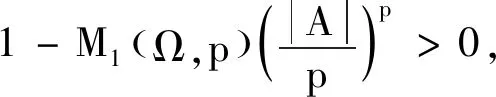

5 结语
