同步转向高地隙喷雾机模糊自适应轨迹跟踪预测控制
2021-10-13刘国海李持衡
刘国海 李持衡 沈 跃 刘 慧
(江苏大学电气信息工程学院, 镇江 212013)
0 引言
农业机械自动导航技术是实现智慧农业以及现代化精细农业的基础[1-3],不仅可以有效降低劳动强度与农业生产成本,还能提高作业精度与作业效率[4-7]。农机路径跟踪方法作为农机自动导航的关键技术也因此得到了长足的发展。农业机械作业环境复杂多变,其自身也具有大时滞、强耦合和高度非线性的特性,这要求农机轨迹跟踪算法具有较好的自适应能力和鲁棒性[8-10]。
目前,农业机械导航控制方法包括PID控制、模糊控制、纯追踪控制、神经网络控制和最优控制等[11]。文献[12]提出的免疫PID控制方法提升了响应速度,并减小了跟踪偏差。文献[13-15]提出的模糊自适应控制方法可以有效提高自主导航控制系统的快速性和稳定性。文献[16]提出的启发式动态规划路径跟随控制方法可以有效提高受控对象的环境适应性和自主优化能力。文献[17]基于纯追踪模型设计了曲线路径跟踪控制算法,其功能可靠,并且具有良好的稳定性和跟踪精度。
同步转向高地隙喷雾机结构新颖,适合在水田环境中工作,但其动力学建模复杂[18],与文献[19-24]中的传统车辆模型以及其他受控对象模型均有较大差异。针对这一问题,本文基于刚体运动学以及几何约束建立用于轨迹跟踪的同步转向高地隙喷雾机运动学模型,并以其运动特点为基础进行简化。在简化模型的基础上建立预测模型,并设计模糊自适应规则,将二者结合提出模糊自适应预测控制策略,基于Matab/Simulink平台进行仿真试验以及场地试验,对模糊自适应预测控制器的性能进行验证。
1 运动学建模
1.1 结构组成
同步转向高地隙喷雾机(图1)主要由控制箱、前后转向桥、轮毂电机、折叠喷杆以及车载导航系统构成。喷雾机的车架主体由多根方形金属管焊接而成。该设计不仅能够有效减轻喷雾机的自身质量,增强负载能力,还能提高喷雾机在平台上的空间利用率。
同步转向高地隙喷雾机的底盘结构(图2)由前、后转向桥以及喷雾机车架组成。
其中,前后转向桥结构相同,分别由1个旋转支承装置、1个支撑桥以及2个由轮毂电机驱动的轮胎构成。前后转向桥分别通过平面轴承和车架前后转向桥中心的A、B相连接。喷雾机前后4个轮毂电机的转矩均独立可控。在喷雾机工作时,前后转向桥可以分别围绕着图2中A、B处2个旋转轴进行旋转,从而实现对车辆姿态的调节。
1.2 同步转向底盘运动学建模
同步转向高地隙喷雾机的运动特点是由其独特的转向机构所决定的。与传统四轮驱动高地隙喷雾机“四轮同时负责驱动,转向机构额外提供转向力矩”的运动方式不同(图3),同步转向高地隙喷雾机可以利用速度闭环通过直接调整喷雾机4个轮毂电机的输出转矩来改变轮毂电机的输出转速,从而对前后转向桥的转角进行调节,最终实现控制喷雾机自身姿态,完成喷雾机前后转向机构同步转向或直行的作业目标。
基于喷雾机的运动情况以及自身工作特点,以喷雾机的初始位置为原点,并在二维笛卡尔坐标系中定义出车辆模型如图4所示,图中x为喷雾机定位横坐标、y为喷雾机定位纵坐标、φ为喷雾机航向角、M为喷雾机定位点、q为前转向桥航向角、p为后转向桥航向角、α为前转向桥转角、β为后转向桥转角、VFl为喷雾机左前轮速度、VFr为喷雾机右前轮速度,VRl为喷雾机左后轮速度、VRr为喷雾机右后轮速度、L为喷雾机左右轮距、D为喷雾机前后轴距。
在运动学模型的设计中,将喷雾机4个轮毂电机的速度(VFl,VFr,VRl,VRr)设为控制量,将喷雾机定位点M的横坐标x、纵坐标y以及喷雾机主轴与X轴的夹角φ(航向角)设为状态量。假设喷雾机在运动时,车轮与地面之间不会发生相对滑动,且喷雾机仅在坐标平面上运动,同时设定逆时针方向为旋转运动的正方向。由此可建立喷雾机的运动学方程为
(1)
(2)
(3)
将喷雾机前后转向桥的运动分解为转向桥绕自身轴心的转动以及跟随喷雾机主体中心M横摆运动。由此,可以推出喷雾机前后转向机构的运动学约束为
(4)
(5)
(6)
(7)
由于喷雾机前后转向桥连在同一个主轴上,于是有一个沿喷雾机主轴方向速度相同的运动学约束为
(8)
假设车轮和地面不打滑,设车轮速度为Vi,半径为d,角速度为ωi,可得车轮角速度与速度的关系为
(9)
其中,i取Fl、Fr、Rl、Rr,表示左前、右前、左后、右后车轮。
1.3 同步转向底盘简化运动学建模
为了增强喷雾机在工作时的抗干扰能力以及转向稳定性,在喷雾机的2组转向桥之间,加入了一个辅助转向链杆,如图5所示[25]。
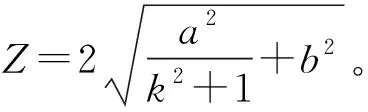
因此,在满足连杆约束的条件下,喷雾机转向时的前、后两组转向桥的转角互为相反数。如图6所示,V1为喷雾机左侧轮胎速度、V2为喷雾机右侧轮胎速度。当喷雾机以固定转向半径进行转向工作时,喷雾机的左、右同侧轮毂电机转速相同(VFl=VRl、VFr=VRr),且喷雾机左、右两侧车轮的轨迹为2个同心圆。而针对传统高地隙喷雾机的简化模型——“自行车模型”并不能够很好地体现出本喷雾机的前后转向桥同步转向的运动特点,并且忽视了车辆在转向时转向桥转角以及车轮转速的变化过程。基于喷雾机以上结构特点与运动特点,可以将喷雾机的整车模型近似简化为具有V1=VFl=VRl及V2=VFr=VRr特性的差速平衡车模型。
在简化设计出“平衡车模型”(图7)的基础上,当喷雾机仅在坐标平面上运动时,可得运动学约束方程
(10)
(11)
(12)
1.4 喷雾机简化模型线性化与离散化
联立喷雾机运动学约束方程(式(10)~(12)),并将其中的位置信息(x,y,φ)分别设置为状态量X和输出量Y,将模型左、右两侧轮胎的速度(V1,V2)设置为控制量u。可以将车辆运动学模型表达为与时间t的相关函数,即
(13)
Y=CX
(14)
其中
X=[x(t),y(t),φ(t)]T
u=[V1(t),V2(t)]T
式中C——3×3的单位矩阵
利用泰勒公式将上述非线性时变系统模型在参考点处展开,转换为线性系统。本文将车辆的目标轨迹以及对应速度设置为参考量
(15)
式中Xr——系统状态参考量
ur——系统输入参考量
将模型在参考点上展开后,只保留一次项,忽略高阶项,有
(16)
(17)
(18)
将式(18)代入式(16)中,可以得出喷雾机简化模型的线性化公式为
(19)
其中
之后对其进行离散化处理。令T为离散时长,便可以得出基于简化模型的离散化线性状态表达式
(20)
其中
A(k)=I3×3+TA(t)
B(k)=TB(t)
2 模糊自适应预测控制系统设计
2.1 预测模型设计
在建立喷雾机预测模型时,为了提高系统的可控性,将前一时刻的控制量加入到预测模型的状态变量中,从而预测模型的状态变量ε为
(21)
式中 Δu(k)——控制量u(k)的变化量
O——零矩阵I2×2——2×2单位矩阵
由式(21)可以递推出ε(k+2)、ε(k+3)、ε(k+4)、…、ε(k+Np)的表达式。设喷雾机的预测模型的预测时长为Np,预测模型的控制时长为Nc(Nc≤Np-1),可以整理出基于模型的预测矩阵为
M(k)=δε(k)+θΔu(k)
(22)
其中
2.2 滚动优化模型设计
在进行目标函数设计时,采用左右两侧车轮的速度为其状态量。同时,为防止系统出现无可行解的情况,引入了权值系数ρ以及松弛因子τ[27],得出目标函数为
(23)
式中Q——状态量权重矩阵
R——控制量权重矩阵
将目标函数展开,并舍弃不可控量,可得目标函数
(24)
其中E=δXr
在试验中,本高地隙喷雾机在控制量上有一定的条件约束。为此在进行二次规划求解时对状态量约束设计为
(25)
式中umax、umin——u(k)上、下限
Δumax、Δumin——Δu(k)上、下限
2.3 反馈校正
由本喷雾机的预测模型可知,Δu(k)为控制量u(k)的增量,将其代入式(21),有
(26)
将式(26)中Δu(k)提取出来并化简,有
u(k)=ur(k)+u(k-1)-ur(k-1)+Δu(k)
(27)
式中ur(k)、ur(k-1)——已知的参考控制量
u(k-1)——已知的前一时刻的控制量
可以通过之前滚动优化模型确定Δu(k)。因此,可以得出最优反馈控制信息u(k)。
2.4 模糊自适应规则设计
预测控制通过计算控制对象的预测状态矩阵,来对目标函数进行滚动优化以及反馈校正来实现对被控对象的控制。预测控制效果与预测时长有关。同时,从之前的预测状态矩阵(式(22))可知,本喷雾机的预测模型矩阵的维度为[3Np,3Np],因此预测控制的运算复杂度与预测时长呈指数相关。当其预测时长较长时,会增加控制系统的运算负担,降低控制效率。当预测时长较短时,虽具有运算量小的特点,但其鲁棒性低,易受到干扰而出现波动。为解决这一问题,本文提出了一种基于实时误差的模糊自适应调整预测时长的方法,如图8所示。
2.4.1输入输出变量模糊化

综合喷雾机的实际性能,对输入输出变量进行模糊化处理:
(1)误差e,基本论域为[0 m,10 m],量化等级为{ZE(零),PS(正小),PM(正中),PB(正大)},量化因子为1。
(2)误差相对于速度的变化率de,基本论域为[-1,1],量化等级为{N(负),ZE(零),P(正)},量化因子为1。
(3)预测时长Np, 基本论域为[20,60],量化等级为{S(小),MS(中小),M(中),MB(中大),B(大)},比例因子为1。
2.4.2模糊规则设计
文献[28]提出,预测控制时长较长的控制系统抗干扰性能好,但运算复杂度高,运算用时长,而预测控制时长较短的控制系统运算复杂度低,但抗干扰性能较差。同时在跟踪误差稳定之后,预测时长不同的控制系统的控制效果相近。在之后的仿真试验中发现,应用预测控制时长较长的控制系统在进行轨迹跟踪时,波动小,超调小但快速性较低。而应用预测控制时长较短的控制系统在进行轨迹跟踪时,快速性好,但会出现较大的超调量。综合以上特性,设计了如下模糊规则:
(1)在误差稳定在一个较小的范围时,表明喷雾机轨迹跟踪稳定,此时输出较短的预测时长来降低系统的复杂度。
(2)在误差小且误差变化率为正数时,说明在跟踪误差较小时由于总扰动,使误差增大,此时输出较长的预测时长来提高轨迹跟踪的抗干扰能力。在误差小且误差变化率为负数时,提高输出的预测时长来防止跟踪时出现超调的现象。
(3)在误差大且误差变化率为正数时,输出较长的预测时长来保证轨迹跟踪的稳定性。在误差大且误差变化率为负数时,输出较短的预测时长来提高轨迹跟踪的快速性。
根据输入输出的模糊化设计以及模糊规则的设计原则可以设计模糊规则表(表1)以及模糊规则曲面图(图9)。
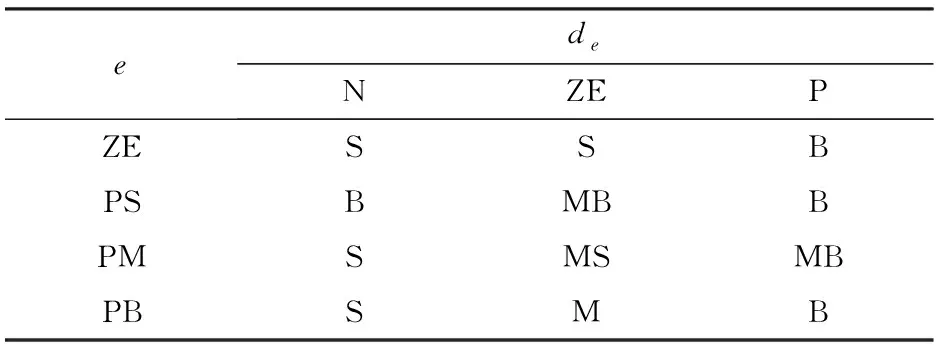
表1 模糊控制规则Tab.1 Fuzzy control regulation
3 仿真试验
为测试所设计的预测控制器的性能,进行了仿真试验。综合同步转向高地隙喷雾机的相关参数,仿真试验的基础参数如下:

将文中设计的模糊自适应预测控制算法即模糊自适应模型预测控制(Model predictive control,MPC)以及预测控制算法用S函数进行封装,并且在Matlab/Simulink平台中建立车辆的运动学模型,最后完成仿真平台的搭建。
3.1 预测控制器控制性能验证
为了验证模糊自适应预测控制器的控制效果和性能,以不同的轨迹为参考目标,与不同预测时长的定参预测控制器进行对比仿真试验。在本次试验中,分别以初始误差为5 m的直线轨迹(模拟变道情景)以及半径为25 m的圆形轨迹(模拟转向情景)跟踪为例,进行轨迹跟踪仿真试验,其结果如图10所示。
从图10b与图10d中可以看出,采用不同预测时长的定参预测控制器在直线轨迹和圆形轨迹的跟踪效果未稳定时,应用预测时长较长的控制器的喷雾机没有超调现象,并且稳定前的波动较少,跟踪2种路径的稳定时长分别为9.03、12.53 s;应用预测时长较短的控制器的喷雾机虽然响应较快,但达到误差零点之后出现了超调现象并产生了波动,跟踪2种路径的稳定时长分别为8.23、11.75 s。从采用模糊自适应预测控制器的喷雾机响应可以看出,它在跟踪直线轨迹以及圆形轨迹的稳定时长分别为6.63、9.62 s。综合试验结果可以看出,模糊自适应预测控制器兼具了轨迹跟踪的快速性与稳定性,其控制效果较定参的预测控制器更好。
在实践中,可以综合实际需求来确定模糊规则,从而达到在保证车辆完成相关工作的前提下,提高控制效率与控制效果的目的。
3.2 预测控制器鲁棒性能验证
对于相关参数变化较少的控制器来说,由车辆定位系统反馈的车辆位置以及航向角的误差,会使得控制器的工作效果下降。由于高地隙喷雾机大多在田间工作,由工作路况不平稳引起的喷雾机侧滑、定位信息反馈不准确的问题会更加突出。模糊自适应预测控制器是通过对当前车辆位置信息的状态反馈来修改自身的控制参数并对控制量进行优化,因此,模糊自适应预测控制器在这种具有不确定性干扰的条件下具有一定的鲁棒性。
在对控制器鲁棒性的验证试验中,将喷雾机状态反馈的干扰用一种白噪声来表示,以此来分析控制器的鲁棒性。在仿真试验中,用来模拟定位信息干扰的白噪声的均值设定为0,标准差设定为0.3 m,模糊自适应预测控制器与定参预测控制器的参数与之前一致,分别对直线轨迹以及圆形轨迹进行跟踪。试验结果如图11所示。
对仿真试验数据进行分析,得出3种预测控制器的控制效果如表2、3所示。从表2、3可以看出,在对2种不同路径进行跟踪时,喷雾机相对于参考轨迹的误差远小于车辆位置反馈信息干扰。

表2 干扰下跟踪直线轨迹仿真结果Tab.2 Simulation results of straight path tracking simulation results in disturbance state m
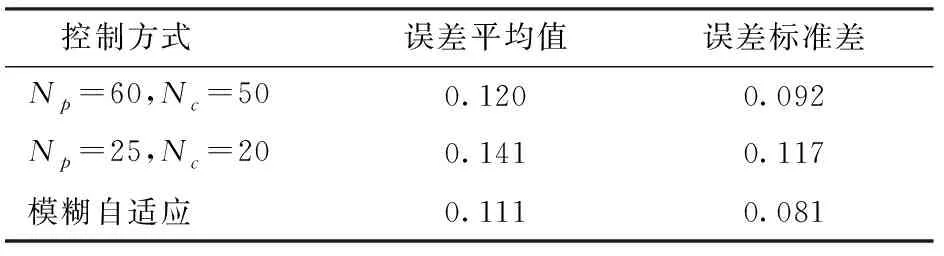
表3 干扰下跟踪圆形轨迹仿真结果Tab.3 Simulation results of circular path tracking simulation results in disturbance state m
从被控对象自身实际的状态反馈来看,在受到干扰时,预测控制器不会因此出现输出控制量的突变,因此车辆的实际状态虽然会受到一定的干扰,但是相对于反馈干扰,被控对象的跟踪效果受到的影响较小。通过对比,相对于定参预测控制器,模糊自适应预测控制器在受到相同干扰的情况下,误差均值以及方差更小,跟踪效果更好。
因此,模糊自适应预测控制器在位置反馈受到干扰时,具有较强的鲁棒性。
4 场地试验
4.1 试验平台
本试验以3WPZ-500型高地隙喷雾机为控制对象,该控制对象目前搭载了由速度控制器、姿态控制器、Modbus通信系统以及前后桥转向角传感器组成的车辆下层控制系统。试验中,采用差分GPS定位系统进行喷雾机的定位。通过实现喷雾机控制系统、导航定位系统,以及模糊自适应控制系统与轨迹规划系统的相互通信,来建立喷雾机轨迹跟踪系统“上层-下层”之间的联系。在本试验中,利用嵌入式计算机来进行导航定位信息处理以及承担模糊自适应预测控制器的功能。嵌入式计算机通过RS-232接口获取从差分GPS定位系统传输来的数据,由Matlab中的导航信息处理程序对接收的数据进行处理,并利用模糊自适应预测控制器生成对应的控制策略;然后将控制信息经由Modbus协议发送至3WPZ-500型高地隙喷雾机;最后喷雾机执行相应动作完成轨迹跟踪任务。由此,设计出基于3WPZ-500型高地隙喷雾机的轨迹跟踪系统如图12所示。
试验场地为江苏大学图书馆广场(32.119 794 610 9°N,119.302 928 414 4°E)。试验场地的路面为石板路(路面平整、硬度适中、略有倾斜),面积约为50 m×50 m,有较大的缓冲空间。试验场景如图13所示。
4.2 直线轨迹跟踪试验
在进行直线型轨迹跟踪试验时,以喷雾机的初始位置为原点,建立二维坐标系。之后,基于此二维坐标系进行目标轨迹的设计。在试验中分别采用初始误差为2.5 m和5 m的直线为目标轨迹。设计喷雾机的初始位置坐标为(0,0),初始航向角为0°,目标左侧轮胎速度V1=1 m/s,目标右侧轮胎速度V2=1 m/s。直线轨迹跟踪试验结果如图14所示。
直线轨迹跟踪稳定后,通过对差分GPS定位系统所记录的数据与目标路径进行对比分析,得出喷雾机直线跟踪结果如表4所示。

表4 喷雾机直线轨迹跟踪数据Tab.4 Straight path tracking data of sprayer m
这2个组别的稳定时间分别为4.8、6.4 s,其稳定时间较短,响应的快速性均较高。
4.3 圆形轨迹跟踪试验
基于之前建立的二维坐标系进行圆形轨迹设计。在试验中采用距离半径为3 m的圆形轨迹为目标轨迹。设计喷雾机的初始位置坐标为(0,0),初始航向角为-90°,目标左侧轮胎速度V1=1.209 m/s,目标右侧轮胎速度V2=0.791 m/s。圆形轨迹跟踪试验结果如图15所示。
通过对差分GPS定位系统所记录的数据与目标路径进行对比分析,得出喷雾机圆形路径跟踪的最大误差为0.117 9 m,绝对误差为0.090 1 m,标准差为0.043 6 m。
4.4 讨论
综合以上数据,可以看出喷雾机以相同的速度进行圆形轨迹跟踪时的准确性略低于直线轨迹跟踪时的准确性。出现这样的现象一方面是由于喷雾机自身对于速度与姿态的响应有一定的延时,这一问题在需要实时更改喷雾机姿态的轨迹跟踪试验中尤为突出;另一方面,由于在进行预测矩阵的设计时,对喷雾机的运动学模型进行了线性化处理,在进行转向运动时由于航向角的变化以及喷雾机自身刚性结构的影响,其非线性、强耦合的特点愈发突出,使得预测模型与喷雾机的实际模型有了较大的出入,因此降低了圆形轨迹跟踪的准确性。
综合喷雾机在直线轨迹以及圆形轨迹的跟踪结果,可以发现虽然其轨迹跟踪的稳定性较好,但是在稳定后会存在一定的波动。除了喷雾机自身控制系统的问题,一方面是由于差分GPS定位系统在进行定位工作时的数据不稳定,这会对轨迹跟踪试验产生一定的干扰;另一方面,因为试验场地有一定的坡度,当喷雾机在这样的场地上行驶时,由斜坡产生的侧向力会对其自身的姿态造成干扰。
综合来看,喷雾机以上3组试验的误差分别为0.044 2、0.060 2、0.090 1 m,标准差分别为0.051 8、0.088 2、0.043 6 m。其误差较小,稳定性较高,可以满足实际生产工作的需求。
5 结论
(1)针对同步转向高地隙喷雾机这种特殊结构的农业车辆建立了运动学模型。为简化控制器的设计,以本高地隙喷雾机的转向特点以及结构特点为基础,建立了简化运动学模型“平衡车模型”。并在简化模型的基础上,综合实际工况完成了模糊自适应预测控制器设计,并分别进行了仿真试验验证以及场地试验验证。
(2)基于Matlab/Simulink平台进行了理想状态以及环境具有干扰的状态下,分别采用模糊自适应预测控制器以及定参预测控制器进行跟踪直线轨迹以及跟踪圆形轨迹的对照试验。从试验结果来看,在理想状态时,所设计的模糊自适应预测控制器可以实现在直线轨迹以及圆形轨迹上的完全跟踪,且相较于定参预测控制器,它兼具了跟踪快速性和稳定性。在具有干扰的情况下,所设计的模糊自适应预测控制器可以较好地抵抗外界的干扰,具有较强的鲁棒性。
(3)在场地试验中,喷雾机以1 m/s的速度分别对直线轨迹与圆形轨迹进行了跟踪。从跟踪结果来看,模糊自适应预测控制器的各种性能均得到了验证,其跟踪结果也可以很好地满足实际需求。
