折叠交叉立方体的分支边连通度
2021-10-12蔡学鹏徐刚刚冯苗苗严玉茹
蔡学鹏,徐刚刚,冯苗苗,严玉茹
(新疆农业大学数理学院,新疆 乌鲁木齐 830052)
1 引言
众所周知,互连网络在并行计算及通信系统中发挥着重要作用.一个网络的拓扑结构在数学上通常被抽象的模型化为一个图G=(V(G),E(G)),其中V(G)是图G的顶点集来表示网络处理器的集合,E(G)是图G的边集来表示网络的通信链路集.在本文中,术语图和网络可以互换使用.本文中所有的图都认为是无向的,简单的和连通的,对于未说明的图论符号和术语,可参考文献[1-2].
G=(V(G),E(G))是一个图.对图G中任意顶点u,设集合

分别表示顶点u的邻点集和邻边集,记为NG(u)和NEG(u).dG(u)=|NG(u)|称为图G中顶点u的度.对图G的子图K,设

分别表示子图K在G中邻点集和子图K在G中的邻边集.设u,v∈V(G),dG(u,v)表示G中连接u与v的一条最短路.对图G的点集X和Y,
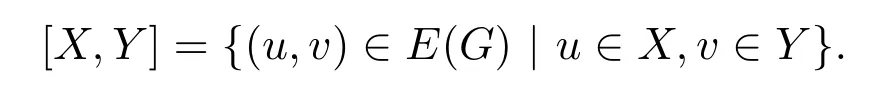
图G中一条具有n个顶点n−1条边的路用Pn=〈u1,u2,···,un〉表示.设x是一个实数,[x]表示不超过x的最大整数.
图G的经典连通度κ(G)和边连通度λ(G)是衡量网络可靠性和容错性的两个重要参数[3].连通度κ(G)和边连通度λ(G)越大,网络的可靠性就越高.但是,这两个参数有明显的不足之处,比如,在一个图中删除相同阶数的点集(边集)后得到的图的分支情况可能会有很大的区别,并且在互连网络的实际应用当中,与一个处理器相连接的所有处理器(链路)同时发生故障是不可能的,所以这两个参数衡量网络可靠性和容错性是不精确的.为克服这些不足之处,自然要去推广图G的经典连通度(边连通度),通过对G-S的每一个分支强加一些限制条件,这里S⊂V(G)(S⊂E(G)).文献[4]首次考虑了这个问题并且提出了图G的条件连通度(边连通度)的概念.
设P是图G所具有的一种性质.文献[4]定义了图G的条件连通度(边连通度):如果G中存在某种点子集(边子集),使得G删除这种点子集(边子集)后得到的图不连通且每个连通分支都具有性质P,则所有这种点子集(边子集)中基数最小的点子集(边子集)的基数称为图G的条件连通度(边连通度),记为κ(G:P)(λ(G:P)).随后,文献[5-6]研究了下面所述的一种条件连通度(边连通度).
设S⊂V(G)(S⊂E(G))且g是一个非负整数,如果G-S是不连通的且G-S的每个连通分支中至少有g+1个顶点,则称S是G的一个Rg-割(Rg-边割).若G存在Rg-割(Rg-边割),则G的所有Rg-割(Rg-边割)中基数最小的Rg-割(Rg-边割)的基数称为G的g-额外连通度(g-额外边连通度),记为κg(G)(λg(G)).有关网络(图)的g-额外连通度(g-额外边连通度)的更多结论可参看文献[7-15].
文献[16-17]各自介绍了经典连通度和经典边连通度另外一种推广形式,即r-分支连通度和r-分支边连通度.设S⊂V(G)(S⊂E(G))且r是一个非负整数,如果G-S至少有r个连通分支,则称S是G的一个r-分支割(r-分支边割).若G存在r-分支割(r-分支边割),则G的所有r-分支割(r-分支边割)中基数最小的r-分支割(r-分支边割)的基数称为G的r-分支连通度(r-分支边连通度),记为cκr(G)(cλr(G)).明显地,cκ2(G)=κ(G)且cλ2(G)=λ(G).因此,r-分支连通度 (r-分支边连通度)可以认为是经典连通度(边连通度)的一种推广形式并且它能更加精确地衡量大型并行处理系统的可靠性和容错性.网络(图)的r-分支连通度(r-分支边连通度)已被许多学者所研究,详细结果可参看文献[18-21]及相关文献.
在并行计算系统中,n维交叉立方体CQn[22-23]和n维折叠超立方体FQn[25]是最重要且最流行的两个互连网络.基于交叉立方体和折叠超立方体,文献 [26-27]介绍了n维折叠交叉立方体网络,记作FCQn.FCQn具有许多重要的特性,比如短的直径、短的平均距离和非常低的消息流量密度.文献 [28]研究了FCQn的点传递性.文献 [7]证明了κ1(FCQn)=λ1(FCQn)=2n,n≥4.文献 [14]证明了λ2(FCQn)=3n−1,n≥5.对于FCQn的详细结果可参看文献[7,26-28].
文献[19]研究了n-维交叉立方体CQn的分支连通度和分支边连通度.文献[29]证明了cκ2(FCQn)=κ(FCQn)=n+1,n≥3和cκ3(FCQn)=2n,n≥4.这篇文章将证明

2 预备知识



3 主要结论



4 结束语
本文在折叠交叉立方体网络经典连通度和2-额外连通度的基础上深入研究,进一步研究了其分支边连通度.证明了:
(1)cλ2(FCQn)=n+1;
(2)cλ3(FCQn)=2n+1,n≥3;
(3)cλ4(FCQn)=3n+1,n≥7.
也就是说,
(1)FCQn至少删除n+1条边才能得到两个连通分支;
(2)FCQn至少删除2n+1条边才能得到3个连通分支;
(3)FCQn至少删除3n+1条边才能得到4个连通分支.
