两时滞广义Logistic模型的Hopf分支与混沌

李顺异, 熊梅,唐兴芸

(1.黔南民族师范学院数学与统计学院,贵州 都匀 558000;2.黔南民族师范学院数学与统计学院复杂系统与计算智能重点实验室,贵州 都匀 558000)

1 引言

英国经济学家,人口学家马尔萨斯(Malthus)在其出版的《人口论》一书中,认为人口按照几何级数增长,建立了著名的单种群增长模型N′(t)=rN(t),其中r为种群的净增长率.考虑到环境因素对种群增长的影响,1838年比利时学者Verhulst提出了Logistic模型N′(t)=rN(t)[1−N(t)/Nm],其中Nm为环境容纳量.种群的增长,不仅受到环境因素的影响,还受到种群内部相互作用的影响.种群内部的相互合作,如群体防卫,群体捕食等对种群的增长起着积极作用,而种群内部的相互竞争,如密度制约,拥挤效应等对种群的增长起着消极作用.种群内部的相互作用对种群的增长,不是立刻体现出来的,而是需要一定时间的,即种群内部的相互合作和竞争,对种群的增长有一定时间的滞后效应[1].

文献[2]构建了时滞单种群模型[2]

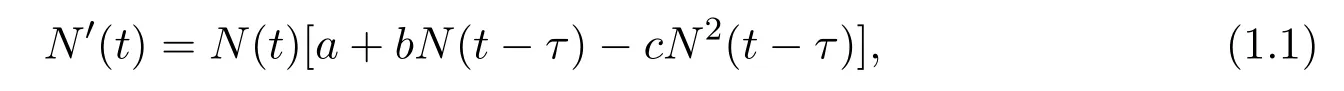
其中b∈R,a>0,c>0.当b>0时,种群的竞争时滞与合作时滞是相同的τ,当b<0时,可视为对经典的时滞单种群Logistic的推广.文献[2]研究了模型(1.1)正解关于正平衡点N∗振动性及正平衡点N∗全局渐进吸引的充分条件.时滞作用是系统不稳定的一个重要因素,往往会使稳定的平衡点失稳而出现周期波动,进而出现更为复杂的动力学行为,如拟周期振动,混沌等[3-8].考虑到种群的竞争时滞与合作时滞不一定是相等的(τ1不一定等于τ2),即使只有竞争时滞作用,不同形式的竞争,其时滞也不一定相等.本文在模型(1.1)的基础上构建两时滞广义Logistic模型

运用特征根方法研究模型正平衡点的稳定性,讨论其发生局部Hopf分支和稳定性切换的条件,分析分支点关于系统参数的单调性和极限性质,并给出数值模拟佐证理论结果.

2 平衡点局部稳定性分析

模型(1.2)有唯一的正平衡点

其在N∗处的线性化方程为

特征方程为

当τ1=τ2=0时,由方程 (2.2)得

由Routh-Hurwitz判别法知正平衡点局部稳定.

3 局部 Hopf分支分析

3.1 情形 1 τ1>0,τ2≡0.

3.2 情形 2 τ1≡0,τ2>0.

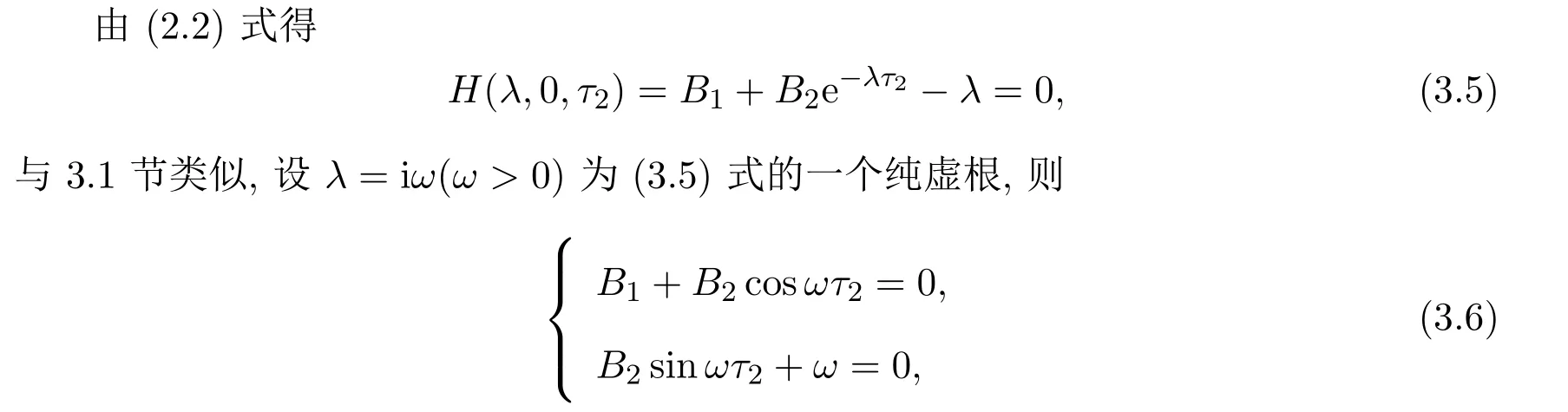
4 数值例子及结论

在模型(1.2)中,令a=2,c=2.5,N(0)=0.5,得b∗=−2.5820.取b=−4.5b∗,由情形 2得,τ1≡0,;取b=−0.9,由情形 3得,τ(0)=0.4702,都在N∗附近发生 Hopf分支 (图 1(b),(c)).

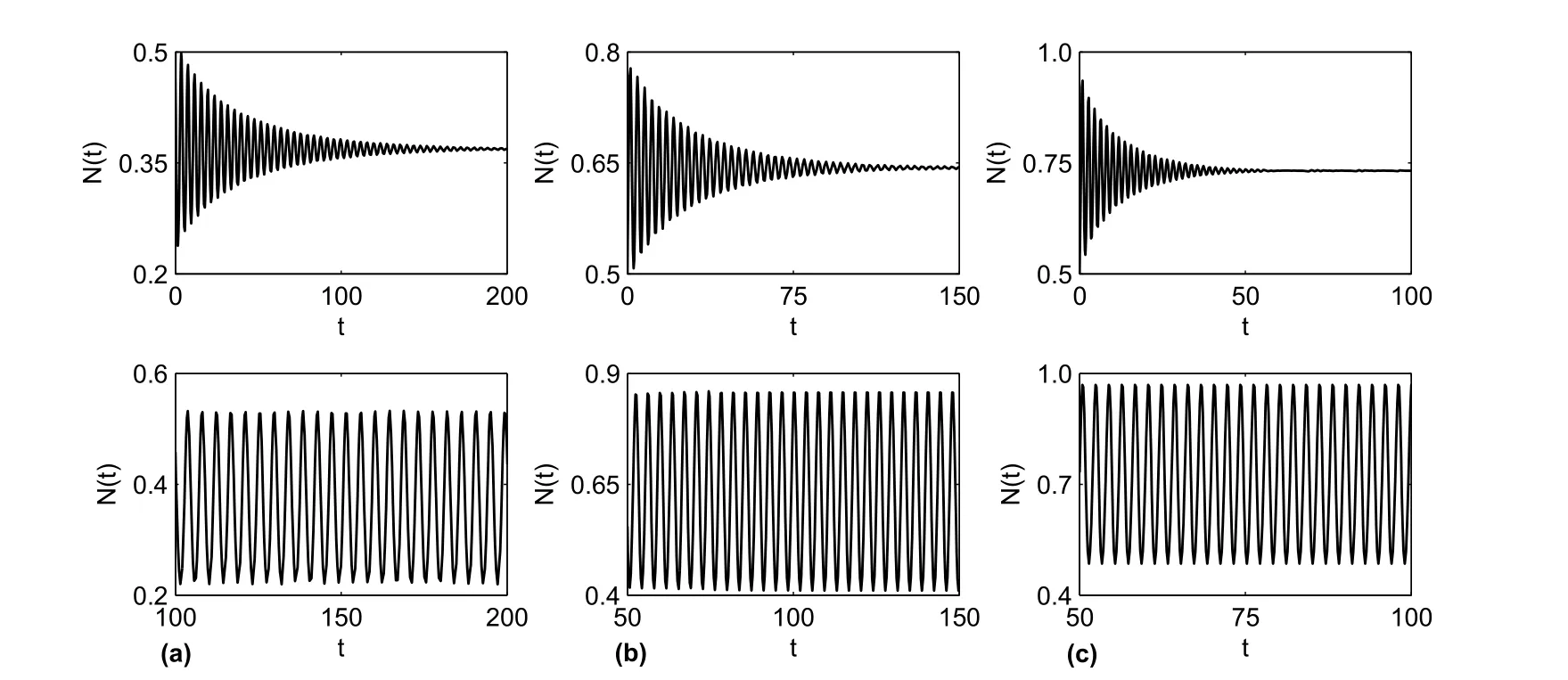
图1 模型 (1.2)的动力学行为:(a)τ2≡0,,;(b) τ1 ≡ 0,,;(c)τ1≡ τ2= τ,τ=0.45< τ(0),τ=0.49> τ(0)

由分支值关于参数b的单调性和极限性质知

这表明情形1(bb∗,τ1≡0)和情形 3(τ1≡τ2)对任何的正数τ∗>0,都存在适当的参数b,使得τ=τ∗成为第一分支值.情形 1(bb∗)都属于条件分支,分支值关于参数b的单调性相反;而情形2是无条件分支,分支值关于参数b严格单调递减.

令b=−4.5,τ1=0.64∈Sτ1,由 (3.19)式得ω1=2.31838,ω2=1.88341,由 (3.20)式得分支值(图2).

图 2 Fτ2(τ1)(ω)=0 和分支值示意图

关于τ2的局部稳定域由5个小区间构成,当τ1=0.64,τ2从0开始增加时,模型(1.2)将经历5次稳定性切换,最终变得不稳定.

进一步,令b=1.5,当τ2=0.3时作出种群N(t)关于τ1在区间 [0.6,1.0]上变化的分支图(图3),由图3知,模型经历了倍周期分支到混沌的动力学行为(图4).

图 3 当 τ2=0.3时,种群N(t)关于 τ1的分支图

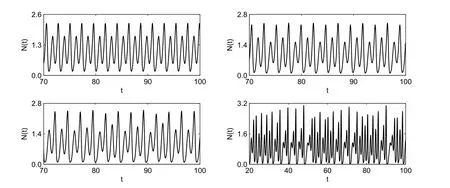
图4 当τ2=0.3时,模型(1.2)的典型动力学行为:τ1=0.7,0.78,0.82,1,2倍周期→4倍周期→8倍周期→混沌

本文基于种群内部相互竞争与合作的基本关系,构建了具有两个离散时滞的广义Logistic模型,详细讨论了各种情况下系统发生Hopf分支和稳定性切换的充分条件.数值例子展示了系统诸如稳定性切换,倍周期分岔,混沌等复杂的动力学现象.