扩散Beddington-DeAngelis捕食食饵模型的行波解
2021-10-12刘欣然肖海滨
刘欣然,肖海滨
(宁波大学数学与统计学院,浙江 宁波 315211)
1 引言
有界行波解是演化PDE一类描述空间状态平移过程的不变解,具有形式
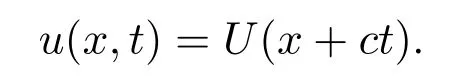
行波解在诸多领域,比如生态种群动力学,燃烧理论,生化反应,疾病传播等,具有广泛的应用.扩散捕食-食饵生态系统的行波解是生物数学研究的一个非常重要的主题,近几十年来一直吸引国内外众多学者的广泛关注,已有大量的研究成果[1-6].当捕食者与食饵间的功能反应函数不依赖捕食者的种群密度时,扩散捕食食饵模型的非负行波解的研究框架较为完整.一般的功能反应的扩散捕食食饵模型可描述为抛物型方程组:
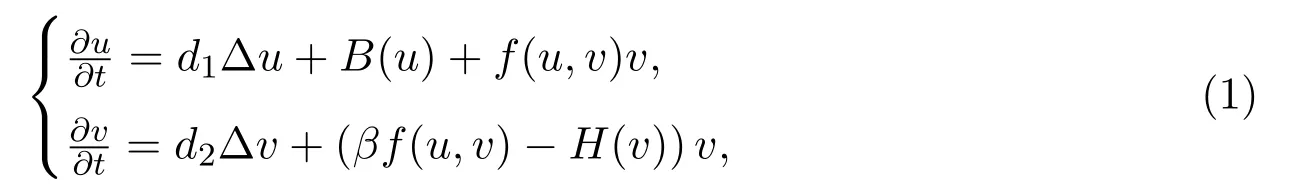
其中u(x,t),v(x,t)分别为食饵和捕食者的种群密度,Δ是Laplace算子,正数d1,d2分别为食饵和捕食者在空间上各自的扩散系数,B(u),−H(v)v分别称为食饵和捕食者的增长函数,f(u,v)称为捕食者对食饵的功能反应函数,而常数β称为二者相互作用的转化系数.
当系统(1)的功能反应函数不依赖捕食者种群密度时,其行波解的研究相对比较完整,Dunbar是研究捕食-食饵扩散系统行波解的先锋.在忽视食饵扩散和考虑食饵扩散的情况下,基于 Wazewski原理和LaSalle不变原理,文献[7-8]应用拓扑打靶方法分别证明:LotKa-Volterra微分方程模型存在连结边界平衡点到共存平衡点的非负行波解.文献[9]又进一步研究了功能反应函数为Holling-Ⅱ型的扩散捕食食饵模型,结合Hopf分支理论,证明了连结边界平衡点到周期轨道的非负行波解的存在性.与此同时,文献[10]应用连结指标理论研究捕食系统的行波解.文献[11]进而综合应用Conley指标,连续性理论和连结矩阵理论,对一类抽象捕食系统建立了各种不同类型的行波解.后来,文献[12-13]基于Dunbar的研究方法和Hopf分支理论分别研究了Holling-Ⅱ型和Holling-III型的捕食系统连结两个平衡点的行波解和小振幅周期波链的存在性.最近十年来,捕食生态系统的行波解仍为应用数学研究工作者的热点主题,涌现出不少重要的研究成果.如有别于众多文献的不同之处,基于有界Wazewski集的构造,文献[14]研究了Sigmoidal型的捕食系统的连结边界平衡点到共存平衡点和原点到共存平衡点的行波解,推广了相关文献的结果.文献[15]应用文献[8]的思想方法研究了具有一般增长函数的扩散Gauss型的捕食系统的行波解,推广了众多文献的相关结论.文献[16]借助于独特的Wazewski集的构造,在忽视食饵扩散和功能反应函数缺少单调性假设的情形下,研究了扩散捕食模型
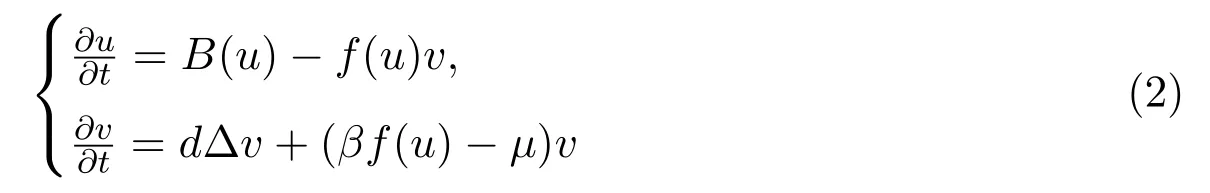
连结边界平衡点到共存平衡点的行波解.据笔者目前所知,文献[16]的结果是对较为一般的上述系统在较为弱的且具有生态意义条件下获得的最优结果.最近,文献[17]进一步考虑了捕食种群具有非线性密度限制的捕食模型,指出文献[16]的结果在这种密度制约下可以保持.
当系统 (1)的功能反应函数依赖捕食者种群密度时,现有文献对其行波解的研究相对比较零散,反应函数主要集中为 Beddington-DeAngelis型.文献 [18]考察了食饵具有 Logistic增长,捕食者具有常死亡率的扩散Beddington-DeAngelis模型,应用文献[7-8]的思想方法给出系统存在连结边界平衡点到共存平衡点的非负行波解的充分条件及临界波速.后来,文献 [19]又进一步利用文献 [16]的方法,把建立半连结轨道的方法推广到功能反应函数依赖捕食种群密度的情形,并应用到具有线性密度制约的 Beddington-DeAngelis模型.接着,文献 [20]总结文献 [16],文献 [19]的思想,把方法推广到考虑食饵扩散的情形,即四维的行波系统,并应用到线性密度制约的Beddington-DeAngelis模型.
正如文献[21-22]指出的那样,不少种群特别是能量级别高的捕食种群的死亡因素不仅仅包括自然死亡,还存在种内竞争,人为破坏等.为此,为方便起见,本文将研究捕食者和食饵都具有一般非线性密度制约的一维扩散Beddington-DeAngelis模型
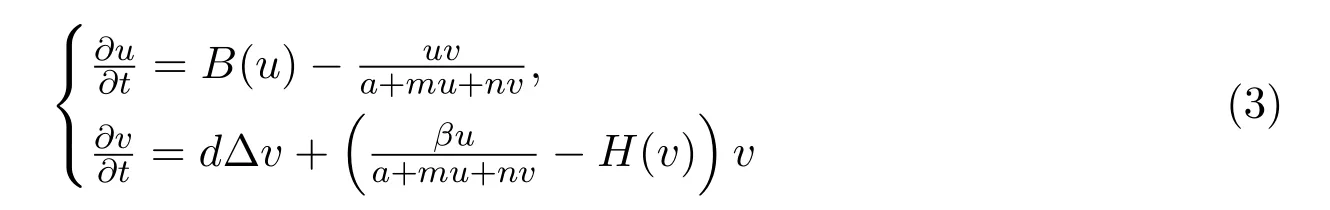
的非负行波解,其中B(u),−H(v)v分别称为食饵和捕食者的增长函数,a,m,n均为正常数,正数d为捕食者的扩散系数,Δ是Laplace算子.具体的结构性假设将在下面给出.当B(u)=ru(1−u),H(v)=µ+δv时,系统(3)即为文献[19]中讨论的线性密度制约模型.
2 模型假设及主要结果
系统(3)的ODE系统如下:


2 基本准备
令u(x,t)=U(x+ct)=U(ξ),v(x,t)=V(x+ct)=V(ξ),代入系统 (3)得其行波系统

易知,(U(ξ),V(ξ))是系统 (5)的解当且仅当 (U(x+ct),V(x+ct))是系统 (3)的解.令cW=cV−dV′,将系统(5)转化为与之等价的一阶方程组
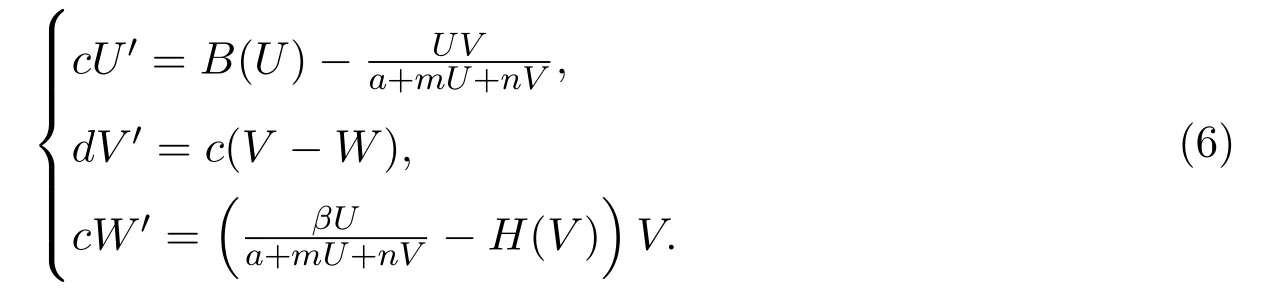
因此,(U(x+ct),V(x+ct))为系统(3)存在连结平衡点EK和E∗的非负行波解当且仅当 (U(ξ),V(ξ),W(ξ)) 是系统 (6) 满足U(ξ)≥0,V(ξ)≥0,−∞<ξ<+∞和边界条件
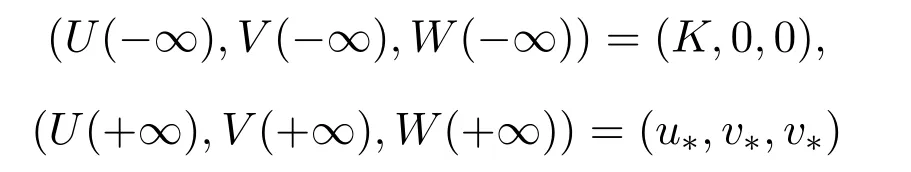
的解,即连结 (K,0,0)到 (u∗,v∗,v∗)的轨道.由于数学符号表示的习惯,系统 (6)的时间ξ仍记为t.系统(6)在(K,0,0)处的线性化系统为
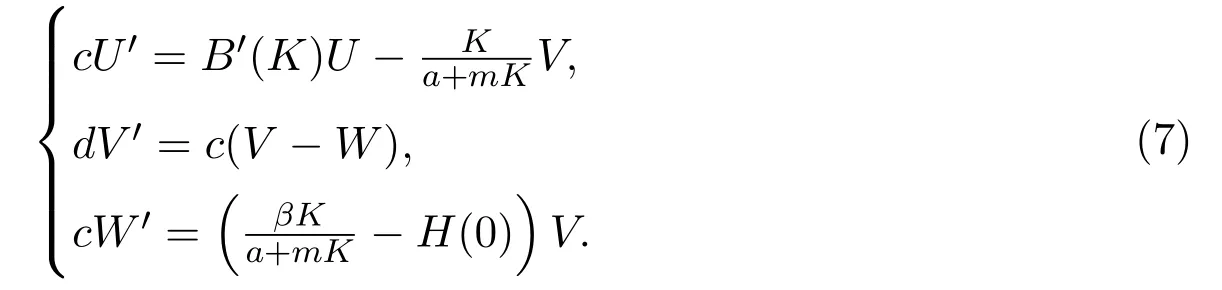
经过计算得到,其系数矩阵有三个特征值

3 定理1.1的证明
通过构造一个Wazewski集来获得系统(6)以边界平衡点(K,0,0)为α极限点的非负半轨道,并利用拓扑打靶法证明此半轨道以共存平衡点(u∗,v∗,v∗)为ω极限点,来证得它即为系统(6)的连结(K,0,0)到(u∗,v∗,v∗)的非负完全轨道.
3.1 Wazewski集的构造


3.2 不变轨道的存在性
本节研究系统(6)在Σ内的以平衡点(K,0,0)为α极限点的不变轨道的存在性.为此考虑研究系统(6)在(K,0,0)处的不稳定流形.系统(6)在(K,0,0)处的线性化系统(7)的特征值λ2,λ3,对应的特征向量分别为



3.3 连结轨道的存在性
对引理3.2.2所建立的Σ内的轨道γ0,本文通过引入它的Lyapunov函数来获得它的V,W分量的一致正有界性,进而证明γ0是连结平衡点 (K,0,0)和 (u∗,v∗,v∗)的非负轨道.



4 总结与展望
基于国内外研究和生态学意义,本论文研究捕食者和食饵皆具有一般非线性密度制约的一维扩散Beddington-DeAngelis模型的行波解,把文献[18]的捕食者和食饵皆具有线性密度制约的Beddington-DeAngelis模型的连结边界平衡点到共存平衡点的行波解的存在性结果推广到了一般非线性密度制约情形.尽管如此,系统(1)功能反应函数依赖捕食种群密度但非Beddington-DeAngelis型时,其行波解的研究仍面临挑战,国内外文献涉足甚少.此外,当不能忽视食饵种群的扩散时,此时的行波系统是四维ODE系统,对于高维的行波系统,如何应用拓扑打靶法,建立系统的行波解有些难度,仍有待研究.
