一种单参变量Bernstein序列及其在含变分数阶非线性边界值问题中的应用
2021-10-11王春秀周星德方立雪金奕潼石贤增
王春秀,周星德,方立雪,金奕潼,石贤增
(1.河海大学 土木与交通工程学院,南京 210098;2.合肥工业大学 土木与水利工程学院,合肥 230009)
分数阶微积分也称为非整数阶微积分,当阶次为常数时,称为常分数阶,当阶次为函数时,称为变分数阶,对于许多材料(如盐岩、聚合物等)来讲,其应力-应变关系采用分数阶描述更为合理[1-2],相应的变分数阶振动控制研究渐渐兴起[3-4]。振动控制从本质上来讲是求解一个边界值问题。有关非线性边界值问题的研究成果较多,但含分数阶的非线性边界值问题(nonlinear boundary value problems,NBVP)研究还较少,目前主要有三种处理方式:其一,采用线性逼近的方式,Jia等[5]分别采用准牛顿法和简化复制核方法把含分数阶的NBVP近似为线性系统,通过迭代方式获得逼近解,其中,分数阶阶次为常数,且计算量偏大;其二,对分数阶进行近似处理,即把分数阶用整数阶多项式近似表示,进而变为普通的NBVP非线性边界值,然后通过常规的数值方法进行求解,Matteo等[6]根据广义微分变换法把RL分数阶变为高阶整数阶表示,进而解出NBVP的解,但由于高阶微分的出现,提供足够的边界值是较为困难的;其三,通过摄动法求解,即对非线性部分采用假设解可以按小参数展成幂级数,可得各级近似方程,进而对级数进行截断得到原方程的渐进解[7]。
对于含分数阶的NBVP,目前研究侧重于通过重构的方式把分数阶近似表示为整数阶多项式形式,诸如移位或加权Jacobi多项式[8]、Chebyshev多项式[9]、Bernstein多项式[10-12]等,由于分数阶,尤其是变分数阶,其表达式复杂,采用常规的正交多项式逼近需要项数较多,可采用改进多项式,如加权Jacobi多项式、超Bernstein多项式等,其处理方式就是在原多项式定义的基础上,引入参变量以加速收敛。Hassani等[13-14]提出的超Bernstein序列(transcendental Bernstein series,TBS),其n+2维多项式构造如下:引入n个参变量,前二项为恒定项,从第三项始,每一项都表示为n个参变量的函数。这种模式对问题的求解无疑是有利且精度较高,但计算难度较大。此外,在目标函数求解方面,目前多采用含变分数阶的NBVP表示为积分形式,附加边界值约束,变为含约束的优化问题,由于非线性的存在,较大可能会出现多解现象,且优化难度也较大。
针对上述存在缺陷,本文以含变分数阶的非线性边界值问题为研究对象,提出一种单参变量Bernstein序列(single Bernstein sequence,SBS),即,从Bernstein序列第三项始,每一项附加一个参变量。相对于TBS,虽然引入的总参变量个数不变,但Bernstein基将变简单,相应的计算难度也会下降。此外,对于含约束的优化问题,若采用诸如拉格朗日乘子法,求解较为困难。为此,本文采用高斯勒让德积分近似目标函数,仿真结果显示此种处理方式可减少优化计算量,且可满足计算精度要求。具体过程如下:首先,引入单参变量构造SBS,进而把变分数阶项转换为SBS为基的多项式表示;其次,对于含积分的目标函数,用高斯勒让德积分近似表示;再次,考虑到非线性优化时存在多解现象,引入遗传算法以期同时获得所有次优解,进而以次优解作为初始值,采用MATLAB优化模块获得最优解;最后,给出了二个仿真实例,结果显示本文方法求解的精度与超Bernstein多项式一样,且均比采用同样维数的Bernstein多项式精度高。
1 含变分数阶边界值问题及Bernstein多项式
设含变分数阶NBVP为

式中:G(·)为非线性算子;α,a,b,c,f均为时变参数;τ为时间t的函数,并且假设在[0,1]区间二阶可微;1<α<2;u0,u1分别为两端边界值参数;为在Caputo定义下的变分数阶微分,表示为
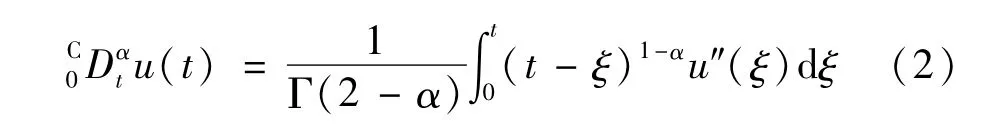
当u(t)=tm时,
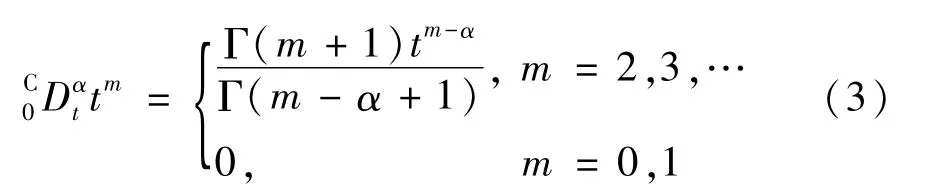
m次Bernstein多项式(Bernstein polynomials,BP)的通项为

2 单参变量Bernstein序列
本文提出的单参变量Bernstein序列,是在Bernstein多项式的基础上,引入参变量si,其通项为
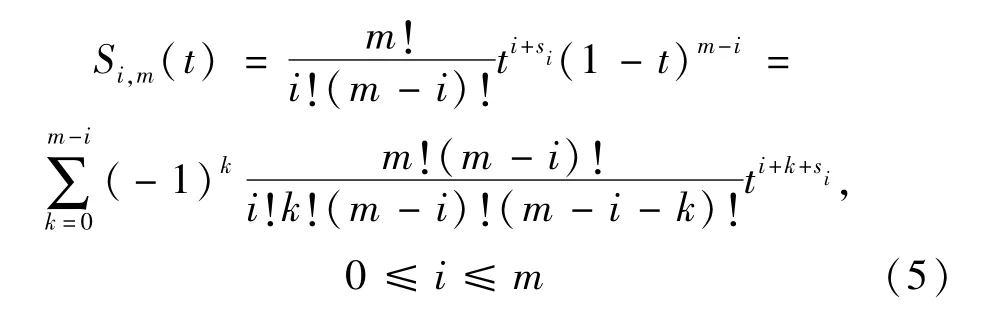
这里需要注意的是,不同于Hassani等提出的TBS,本文提出的SBS,从第三项起,每一项均包含1个参变量。
以i=4(m≧4)为例:
SBS
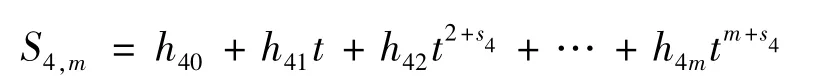
TBS

其中,

有关SBS收敛性证明如下:
定理1假设μ是函数J在Cn[0,1]内的最优解,若μn是J在Cn[0,1]∩Y内的最优解,则有[15]

定理2假设g(t)∶[0,1]→R是一个连续函数,对于任意t∈ (0,1)且 ε>0,存在一个SBS,使成立。证明如下:
给定一个任意数ε,利用维尔斯特拉定理[16],通过多项式有

因此,此处令

构造一个实数数列{si,n},当n→∞时,参变量si,n→si,这就说明,当n→∞时,tsi,n→1/ci,其中ci=(i! (mi)!)/(m! (1-t)m-i)。 对 于 任 意 的 ε>0, 有
存在v=max{N0,N1,…,Nm∈N}, 使

证明完毕。
3 数值算法
以SBS为基函数,u可近似表示为

式中:CT=[c0c1…cm]为待定常数;Sm(t)=[1 t S2,m(t)S3,m(t)…Sm,m(t)]T。
对于Sm(t)的变分数微分根据式可近似为矩阵形式,为
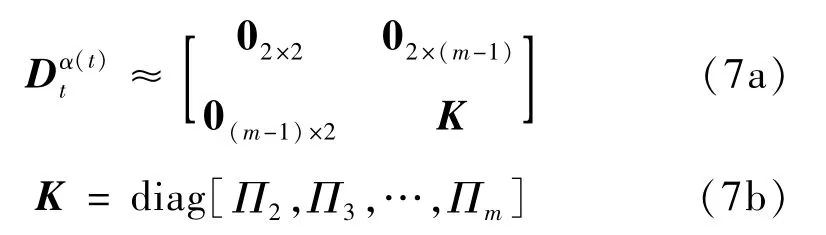
同理,对于Sm(t)的一阶微分,可近似表示为,其中为

根据变分数阶和一阶微分表示,可以得到下列展开式

将式(9)代入式(1),得
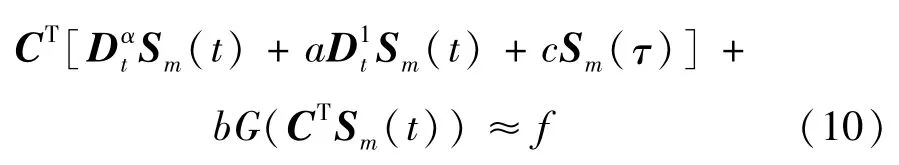
目标函数定义为
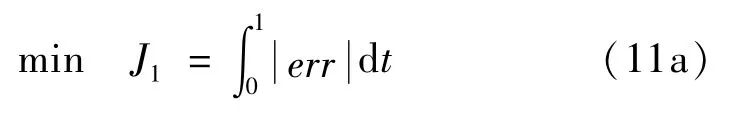
也可以取目标函数为
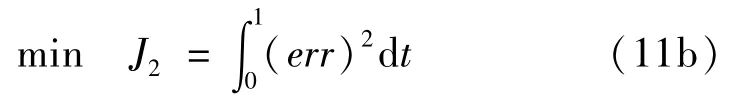
其中,
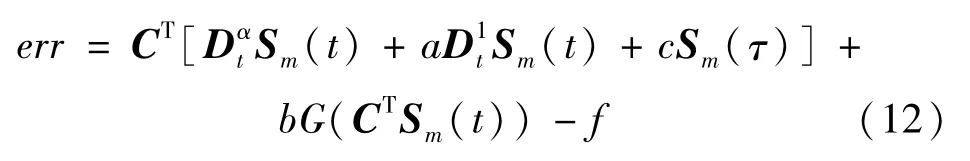
优化的约束条件为式(1)中的边界条件,为

目标函数J1计算相对简单,但在优化过程中,由于绝对值的存在,err曲线会出现尖点,优化时可能出现奇异,适合于不太复杂的非线性边界值问题;目标函数J2计算较为复杂,但在优化过程中,err曲线不会出现尖点,优化时出现奇异概率较小,适合于较为复杂的非线性边界值问题。
采用拉格朗日乘子法求解非线性边界值较为困难,因此,本文采用(q+1)点高斯勒让德积分形式对式(11a)、式(11b)进行简化

式中:δk为勒让德多项式的零点;wk为相应的权值。
4 遗传算法
考虑到非线性优化时存在多解现象,而常规优化得到的最优解往往与初始值相关,为避免漏失最优解,本文引入遗传算法以期同时获得所有次优解,进而将次优解作为初始值代入MATLAB优化模块获得所有最优解。
考虑到本文优化约束中含有自变量,把其作为个体,在遗传算法中,只能先确定自变量所在区间[d,e],
但这个区间不易确定,可以先选择大的范围,根据优化结果来缩小区间。在个体产生方面,为简化计算,此处,直接采用十进制数产生,为

式中:Rand为介于0~1的随机数;pi为第i个自变量。
交叉和变异均采用式(15)产生新的个体,适应度取

5 算例分析
本章将通过两个算例证明上述所提算法的精确性和可行性。在ti∈[0,1]上的绝对误差值定义为
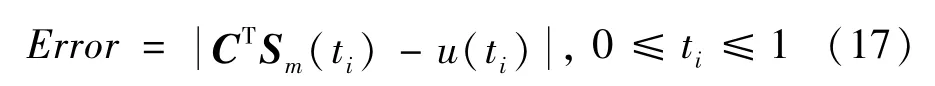
例1
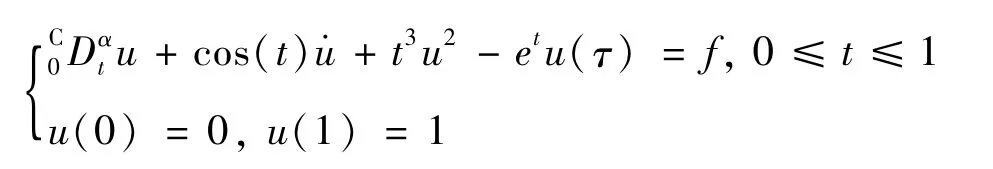
其中,
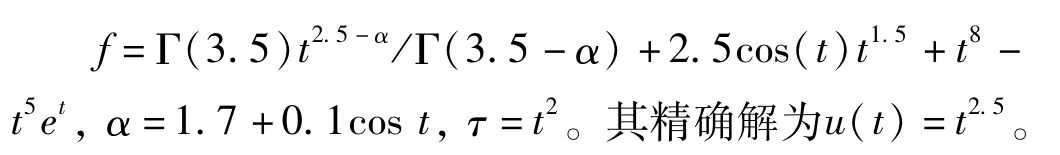
采用m=3的SBS为基函数,以式(11a)作为目标函数形式,通过5点高斯勒让德积分方法对该问题进行近似。

其中,c0,c1,c2,c3和s2,s3均为未知量。
由hij组成的系数矩阵H可表示为
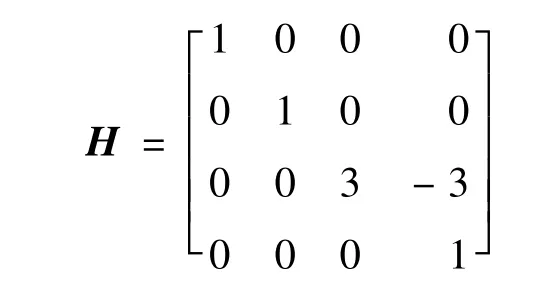
因此,近似解可表示为u(t)≈CTS3(t)。
根据式(7),变分数阶微分算子矩阵中K为
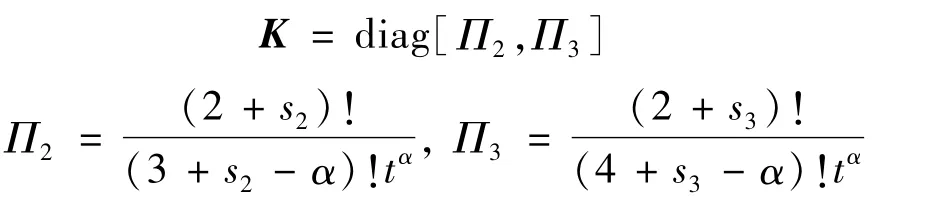
根据式(8),一阶微分算子矩阵中Z为
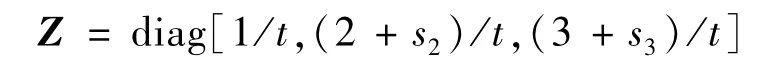
式(14)表示的边界条件为

根据以上计算可得到本例的目标函数

其中,

利用遗传算法,初始时各未知变量取值区间为[-300,300],可以通过优化结果来缩小各个变量区间。所有变量的初始群体均为200,考虑到遗传算法的优化结果仅仅作为采用MATLAB优化的初始值,这里,误差取为2.0,限于篇幅,此处仅列出m=3时各变量最终取值范围:s2为[-20,20],s3为[-1,1],c1为[-0.5,0.5],c2为[-1,1],根据边界条件可知c0=0,c3=1-c1。由遗传算法得到的部分结果(见附表1)确定MATLAB优化模块中所需要的初值,此处取初值为:s2=0.550 6,s3=-0.612 9,c0=0,c1=-0.081 1,c2=-0.050 1,c3=1.081 1从而得到未知参变量最优解


表1 不同m值SBS和BP的绝对误差Tab.1 The absolute errors of SBS and BP to different m
为了对比分析,笔者还用同样的优化方式求解该例题在BP基函数下的近似解。当t在[0,1]内时,取不同的m值,通过SBS方法和BP方法求得的近似解与精确解的绝对误差情况见表1。使用BP法时产生的绝对误差曲线见图1(m=3(图1(a))、m=5(图1(b))。结果表明,在SBS方法下的结果比使用BP方法精确度更高。
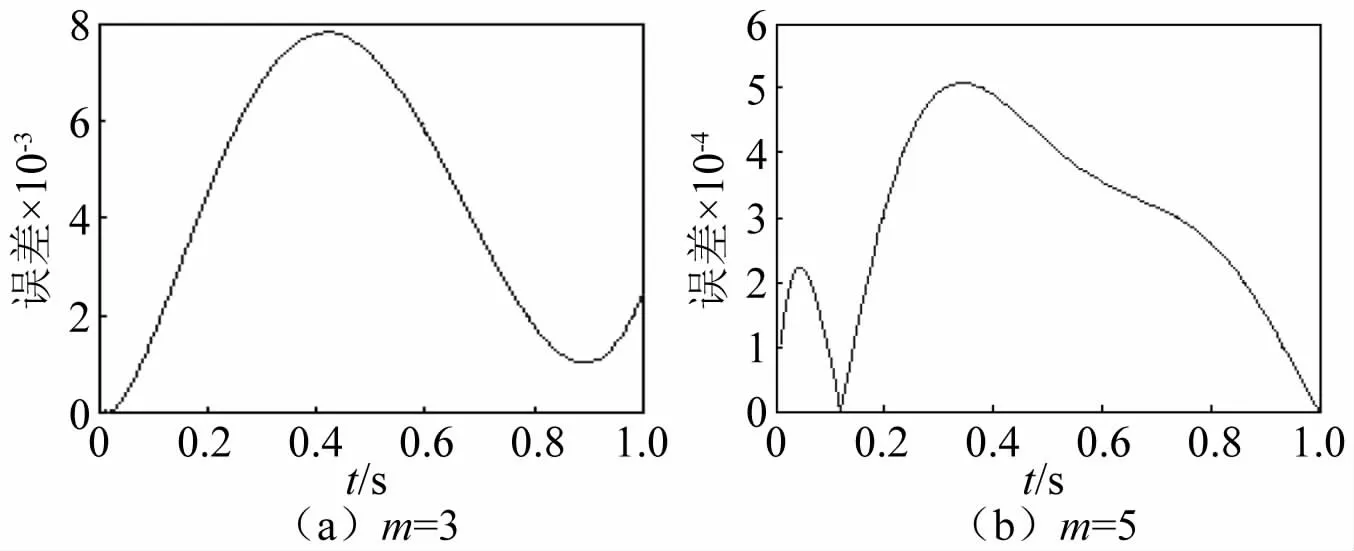
图1 采用BP近似时的绝对误差Fig.1 The absolute errors when using BP approximation
例2变分数阶非线性Troesch边界值问题

当α=2时,精确值在文献[17-18]中给出。针对不同的m和α值,以式(14b)作为目标函数,通过7点高斯勒让德积分方法对该问题进行近似。图2给出了m=4时,α=2,θ=0.5(图2(a))和 α=2,θ=1(图2(b))的近似曲线和精确点值的吻合情况。图3给出了m=4,θ=0.5(图3(a))和m=4,θ=1(图3(b))时,α函数分别取1+0.1cos t2,2-0.2exp(-10t),2-(sin t)2/5,2的近似曲线。结果表明,本文提出的SBS数值方法精度较高,且无论α函数如何选取,u的近似曲线都很稳定,说明此方法稳定性较好。
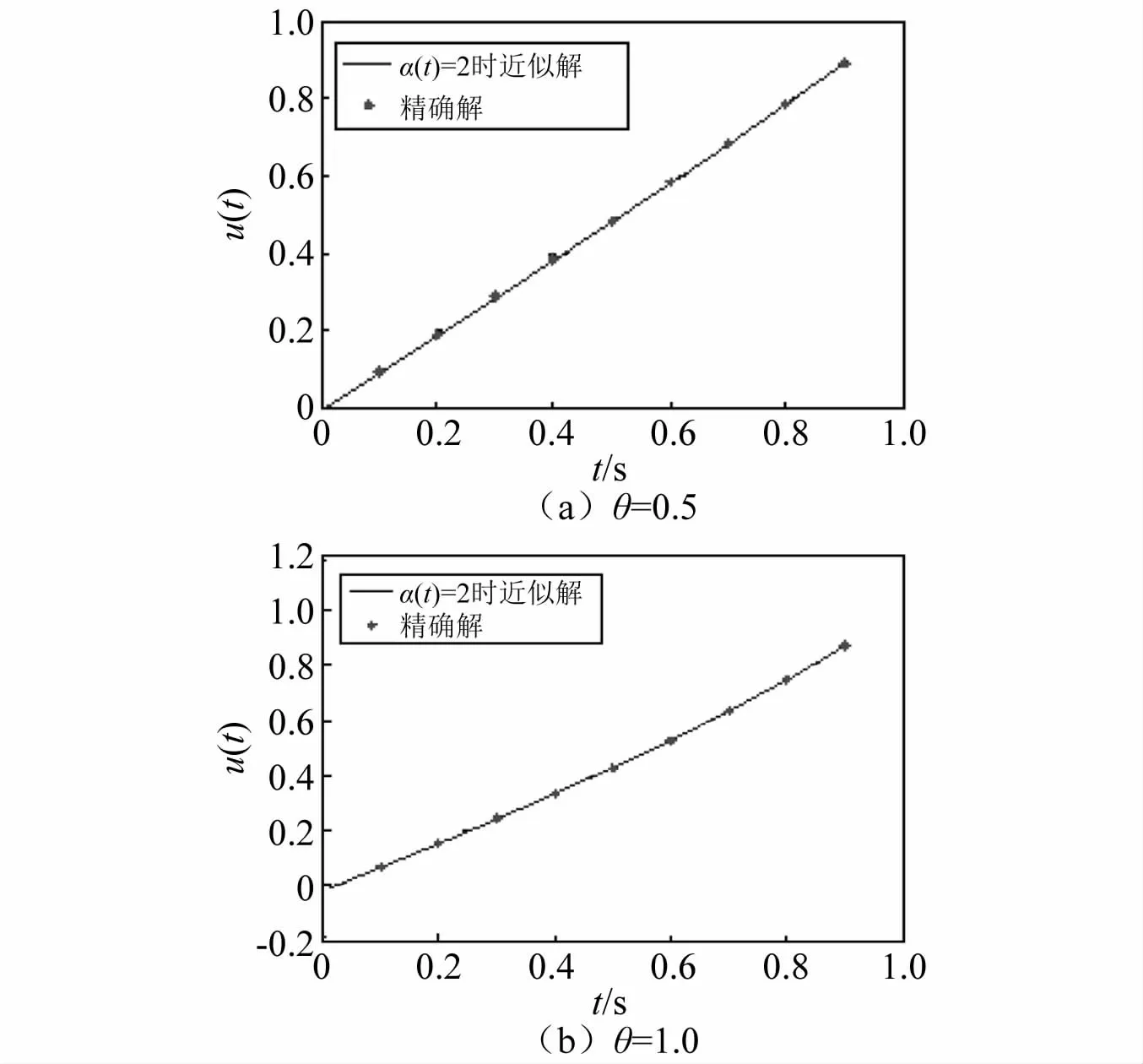
图2 α=2时SBS近似解与精确点对比Fig.2 The SBStechnique compared with the exact solution withα=2

图3 不用α函数时SBS近似曲线Fig.3 The approximate solution based on SBSto different functionsα
6 结 论
本文在Bernstein多项式和Hassani等提出的超Bernstein序列的基础上,提出了单参变量Bernstein序列,以SBS为基函数解决非线性变分数阶边界值问题,得出如下结论:
(1)所提出的SBS,从第三项目始,每项仅含有一个参变量si,和Hassani等相比计算量大幅减少。
(2)针对积分表示的优化目标,利用高斯勒让德积分方法近似减少计算量,从实例结果来看,精度也可满足。
(3)考虑到非线性优化时存在多解现象,通过引入遗传算法同时获得所有次优解,进而以次优解作为初始值,采用MATLAB优化模块获得最优解,此种处理方式可有效避免漏失最优解现象。
(4)算例分析表明引入参变量可扩展BP的实用性。
附录A

表A.1 遗传算法所得的部分次优解及适应度Tab.A.1 Partial sub-optimal solutions and fitness of using genetic algorithm
