初始条件对男子投掷标枪飞行远度影响的分析研究

2021-10-11王守忠郜春霞刘玉莹

三门峡职业技术学院学报 2021年3期

◎王守忠郜春霞刘玉莹

（商丘职业技术学院农学院，河南商丘476100）

投掷标枪是田径项目中极为复杂的一项运动[1]。其基本技术是由肩上持枪经过一段预先助跑连接投掷步获得动量，最后用力将标枪经肩上投出去。研究表明，在投掷标枪的最后用力阶段结束以后，标枪在空中飞行的远度主要与运动员投掷标枪初始条件、标枪的参数和环境因素等有关[2]。标枪的参数和环境因素是运动员无法改变的，只能在运动实践中予以适应或把握，运动员所能控制和改变的因素主要是标枪飞行的初始条件。因此，在决定标枪飞行远度的诸因素中，初始条件对标枪飞行远度影响的试验研究一直是教练员、运动员和广大学者关注的热点问题。

目前，国内外对投掷标枪各初始条件的研究多数还停留在理论水平上，与运动实践的结果有较大的出入。如有的在研究初速度对标枪飞行远度的影响时，假定初始攻角为零度[3]，忽略了标枪在空中飞行时，只有攻角不为零度时，才能够获得空气动力积极效应这一必要条件；在对标枪的飞行轨迹进行研究时，假定标枪飞行时是在垂直平面运动[4]。也有的研究限于条件，还只是从局部最优条件出发，对于决定标枪飞行远度因素的分析尚不够全面系统，使人们对影响标枪飞行远度的诸多因素以及它们之间的相互关系缺乏辩证认识。因此，系统的研究各初始条件对标枪飞行远度的影响，对于运动员在标枪比赛中取得优异的成绩具有重大的理论和实践意义。

1 研究对象与方法

通过查阅相关中外文献资料、教材、专著和对影视资料进行截图、拍照等途径获得国内外500 余名优秀男子标枪运动员出手时的技术图片和已有的运动学参数。通过分类整理，参考已有的研究成果[5-10]，采用APAS System 解析系统对获得的图片进行解析、判读后，借助于计算机，应用数字滤波法对原始数据平滑处理，截断频率为8Hz，解析出研究所需要的各初始运动学参数。用Excel2014 和Slassl2.0 软件对获得的原始数据进行统计分析和模拟计算。在定量分析初速度、出手角度、初始攻角、初始俯仰角速度、初始偏航角、旋转速度等初始条件对标枪飞行远度的影响的基础上，从运动生物力学、空气动力学、物体斜抛运动学等角度揭示了各初始条件对标枪飞行远度的影响规律以及各初始条件彼此之间的内在联系，并分析探讨了各初始条件最佳组合形式，力图为运动员、教练员进行科学的训练提供启示或借鉴。

2 研究结果与分析

2.1 初速度对标枪飞行远度的影响

在运动员投掷标枪的初始攻角、初始俯仰角速度和初始偏航角为定值的前提条件下，不同初速度V0对标枪的飞行远度的影响分析计算结果如表1 所示。

由表1 可知，当运动员的出手角度为β=34°时，投掷标枪的飞行远度随着初速度的提高而增加，在初速度为（26—30）m/s 的范围内，初速度每增加1m/s，飞行远度增加5m 左右，当初速度继续增加时，飞行远度增加的幅度有加大的趋势。模拟计算结果表明，除垂直向上投掷标枪外，标枪在空中飞行的远度与初速度呈正相关系。

表1 初速度对标枪的飞行远度的影响表（m）

2.2 出手角度对标枪飞行远度的影响

在运动员出手的初速度、初始俯仰角速度和初始偏航角为定值的前提条件下，不同出手角度对标枪的飞行远度的影响分析计算结果如表2所示。

从表2 可见，当初速度为28m/s 时，随着出手角度的增大，标枪的飞行远度增加，当出手角度在（30—32）°范围内增大时，标枪的飞行远度增加幅度较大，当出手角度大于32°时，标枪的飞行远度增加幅度较小。当出手角度达到42°时，标枪的飞行远度反而下降。模拟计算结果表明，标枪的飞行远度与出手角度并非正比例关系，只有将标枪的出手角度控制在（30—32）°范围时，才能使标枪飞行的更远。

表2 出手角度对标枪的飞行远度的影响表（m）

2.3 初始攻角对标枪飞行远度的影响

当运动员投掷标枪的初速度为30m/s、出手角度在（30—40）°之间增大时,不同初始攻角A0对标枪的飞行远度的影响分析计算结果如表3所示。

表3 初始攻角对标枪的飞行远度的影响表（m）

从表3 可见，初始攻角对标枪的飞行远度的影响不仅与自身的大小有关，而且还与出手角度的大小有关，当出手角度较小时，如果初始攻角＜0°或＞0°，则标枪在空中飞行的远度逐渐下降；当出手角度较大时，如果初始攻角＜0°，则标枪在空中飞行的远度则先增大后减小；当初始攻角＞0°时，则标枪在空中飞行的远度则逐渐地下降。当出手角度较小时，最佳初始攻角为（0—3）°，当出手角度较大时，最佳初始攻角为（-3—9）°之间，而当初始攻角为正值时，不同出手角度下标枪飞行远度均下降。模拟计算结果表明，适宜的初始负攻角是使得在空中飞行更远必要条件之一。

2.4 初始俯仰角速度对标枪飞行远度的影响

当运动员投掷标枪的初速度为28m/s、出手角度为42°时，初始俯仰角速度对标枪的飞行远度的影响分析计算结果如表4 所示。

从表4 可见，初始俯仰角速度对标枪的飞行远度的影响不仅与自身的大小有关，而且还与初始攻角的大小有关。当初始攻角一定，初始仰俯角速度≤0°/s 时，在初始攻角为（0—6）°范围内，标枪的飞行远度先增大后减小；在初始攻角为（0—6）°范围内，标枪的飞行远度逐渐增大。当初始俯仰角速度＞0°/s 时，在初始攻角为（6—6）°范围内，标枪的飞行远度逐渐减小。当初始俯仰角速度在（-15—15）°/s 的范围内变化时,不同初始攻角下，标枪的飞行远度相差最大为7m 以上,这正是同一名标枪运动员在几次投掷标枪时，虽然出手速度、出手角度相差无几，但运动员的成绩却出现较大的差异的原因所在。模拟计算结果表明，初始俯仰角速度为零时可使标枪飞行得更远，也就是说运动员在投掷标枪时，作用在标枪上力的方向必须与标枪纵轴方向一致，要想使得运动员做到这一点通常是十分困难的。当初始攻角大于最佳值时，如果有一个合适的负初始俯仰角速度与之配合，可以纠正这一错误，使标枪飞行得更远。

表4 初始俯仰角速度对标枪的飞行远度的影响表（m）

2.5 偏航角对标枪飞行远度的影响

当运动员投掷标枪的初速度为28m/s、出手角度为32°时, 不同初始偏航角D0对标枪的飞行远度的影响分析计算结果如表5 所示。

从表5 可知，不同初始攻角下，随着初始偏航角的增大，标枪的飞行远度逐渐减小，在0°-18°范围内标枪的飞行远度下降幅度较小，初始偏航角≥20°时标枪的飞行远度下降幅度明显增大。模拟计算结果表明，运动员在投掷标枪时应尽量避免初始偏航角超过20°，否则会使投掷成绩大幅度下降。

表5 初始偏航角对标枪飞行远度的影响表（m）

2.6 旋转速度对标枪飞行远度的影响

当运动员以初速度25m/s、出手角度36°及初速度27m/s、出手角度34°投掷标枪时，标枪旋转速度从0 增加到30 周/S 时，旋转速度对标枪的飞行远度的影响分析计算结果如表6 所示。

从表6 中可知，不同初速度和出手角度下，随着自转圈数的增加, 对标枪飞行远度的影响极小，最大不超过2%。这与一些文献或著作中认为标枪出手时具有较大的自转速度对标枪飞行的稳定性会产生良好影响，并会增加飞行远度有很大的差异[11-12]。模拟计算结果表明，旋转速度对标枪飞行远度的影响是有限的，试图通过提高标枪旋转速度来提高投掷标枪飞行远度的做法值得商榷。

表6 自转圈数对标枪的飞行远度的影响表（m）

2.7 初始条件最佳组合形式探析

标枪在空中飞行时的初速度、出手角度、初始攻角、初始俯仰角速度、初始偏航角等，同处于一个系统中，他们既独立存在，又相互制约，各自的作用和功效不同。只有各初始条件按最优结构有机地组合在一起时才能使标枪飞行得更远。

相关研究表明，能使标枪获得最大初速度的条件是：运动员要具备较好的力量素质和速度素质以及良好的协调性，对最后用力技术通常要掌握得相当好[13-14]。这需要运动员经过长期的训练才能够达到。因此，一名运动员的出手速度在较短的时间甚至在某一个较短的运动周期内一般很难有较大的改变，可以认为是定值。另外，其身高臂长在短期内也不会发生太大的变化，也可以认为是定值。因此，运动员在短期内投掷标枪出手时各初始条件可能出现的组合形式主要有下列三种情况：

第一种组合形式：姿态角θ＞出手角度β，攻角 A0＞0°，初始俯仰角速度 ω＞0°/s，空气动力压心距P 为负值，如图1 所示。

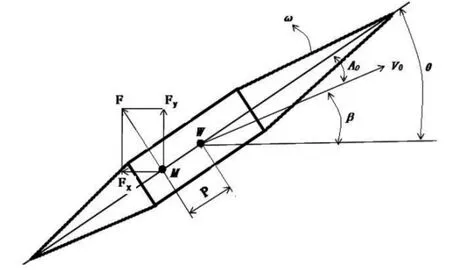
图1 第一种组合形式示意图

在这种组合形式下，由于 θ＞β，A0＞0°，从而导致空气压心M 位于标枪的重心W 后面并向枪尾方向移动，则会造成空气动力压心距P 增大，则标枪的初始俯角速度ω 增大，致使枪尖抬头，枪尾下沉。作用在标枪压力中心上的空气动力F 的水平分量FX 与标枪向前运动的方向相反，抵消了一部分出手初速度V0的水平速度，缩短了标枪的水平飞行距离；F 的垂直分量Fy为正升力，虽然能够使标枪升得较高，但水平速度减小，标枪飞行一段距离以后，便迅速下降，减小了标枪的飞行远度。显然这种组合形式没有很好地利用空气动力效应。

第二种组合形式：姿态角θ＜出手角度β、攻角 A0＜0°、初始俯仰角速度 ω＜0°/s、空气动力压心距P 为负值，如图2 所示。

图2 第二种组合形式示意图

在这种组合形式下, 作用在标枪压心上的空气动力F 的水平分量FX 与标枪向前运动的方向相同，变成动力，加大了标枪飞行的水平速度，则标枪上抛阶段飞行的水平距离增大；F 的垂直分量Fy 为负升力，使得初始攻角的绝对值增大而使标枪抬头，此时适宜的负初始俯仰角速度可以阻止标枪过于抬头，使标枪飞行得更远。当A0＜0°时，空气动力压心前移，压力中心的位置距离标枪重心较近,标枪的下俯的力矩减小，空气动力的效应能够延长标枪在空中滑行的时间，则下抛阶段标枪滑翔的水平距离也越远。

第三种组合形式：θ=β，A0=0°，ω=0°/s，P＜0，FX 为动力，如图3 所示。这实际上是人们在投掷标枪时的一种理想组合形式，也就是说，投掷标枪时运动员作用在标枪上力的方向必须与标枪纵轴线方向一致。

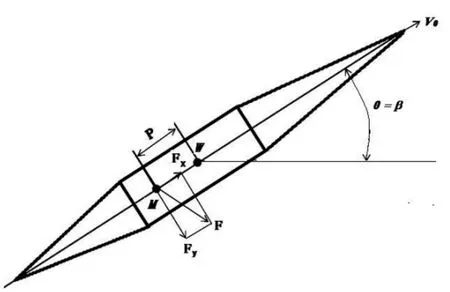
图3 第三种组合形式示意图

在这种组合形式下，虽然标枪也是流线型器械，但它在空中的飞行速度相比飞机、子弹之类的流线型物体在空中飞行的速度要低得多，即标枪在空中的飞行运动属于低速运动。由空气动力学理论可知，当A0=0°时，空气流对低速运动的标枪产生的气动力只有黏性摩阻力和黏性压阻力，阻力值较小，理论上标枪的飞行距离会越远。但同时，空气动力作用在标枪上的升力也将变得很小，标枪出手后没有明显的上升过程，也没有特别的下降弧线，减少了标枪在空中飞行时间，标枪的飞行速度虽然相对较快，但标枪落地的角度很小，有时裁判员会较难找准标枪落点，容易导致无成绩，即使有成绩，由于标枪在空中飞行时间较短，成绩也不会太理想。这是因为决定标枪成绩的关键要素不是阻力，而是升力与阻力的比，而升力与阻力是同时并存的，在减小空气阻力对标枪进动性影响的同时也应适当考虑空气升力对标枪在空中飞行时间的影响。

另外，由于现代男子比赛用标枪重心又前移4cm，标枪压心距绝对值相对增大，致使标枪轴沿逆时针方向转动的可能性增大。而标枪的重心又靠近标枪绳把前沿，运动员在投掷标枪时，手通常握在标枪绳把后沿K 点处，如图4 所示，在运动员最后用力出枪瞬间，手指会对标枪施加一个向前下方的拨动力F，该力可以分解为沿标枪纵轴分力F1和垂直于纵轴的分力F2。F1驱使标枪做斜抛运动，F2驱使标枪沿纵轴旋转的同时还会产生一个逆时针方向的力矩F2×P,使标枪抬头，此时标枪在空中的飞行的攻角便会大于零度[15]。当姿势角θ 稍大于出手角时，标枪就以正攻角飞行，转化为图1 所示的组合形式；当姿势角θ 小于出手角β 时，标枪就以负攻角飞行，转化为图2 所示的组合形式。因此，在运动员实际标枪投掷的过程中，出现第三种组合形式几乎是不可能的。

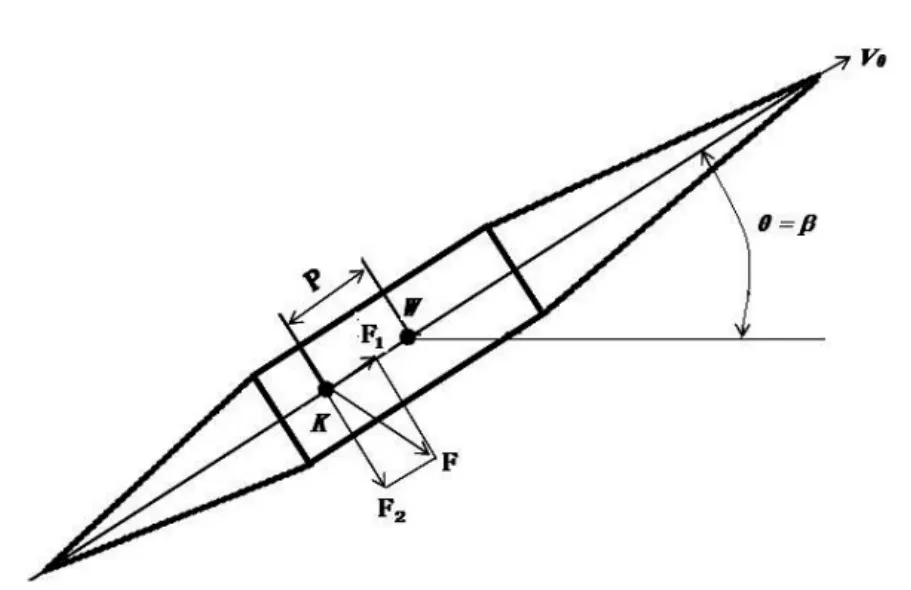
图4 标枪出手瞬间手指作用力示意图

2.8 研究结果分析

通过上述计算分析发现，初速度是影响标枪飞行远度的必要条件，但并不是充分条件，而是和出手角度、初始攻角、初始俯仰角速度和偏航角等协同作用的结果。当运动员投掷标枪的初速度发生变化时，出手角度也随之改变，当出手角度改变时，标枪的初速度和最佳初始攻角等初始条件也会随之发生变化。当出手角度较大时，初速度下降，最佳初始攻角较小；当出手角度减小时，初速度与最佳初始攻角均增大，当最佳出手角度确定后，与之对应的最佳攻角是个区域值。当初始攻角增大时，适宜的初始俯仰角速度将产生一个使标枪低头角速度，来弥补初始攻角增大时的负面影响，在一定范围内也可使标枪达到较大的飞行远度。不同大小初始偏航角都会对标枪的飞行远度产生一定的负面影响。在不同初速度和出手角度下，随着自转圈数的增加，对标枪的飞行远度影响极小。当运动员出手初速度和高度一定时，其他各初始出手条件最佳组合形式为第二种组合形式。

研究分析发现，每个男子标枪运动员都有自己的投掷风格，如2018 年全国投掷系列赛（成都站）前三名标枪运动员与国外优秀标枪运动员不同初始条件与投掷成绩对照统计结果如表 7 所示[16-17]。

表7 不同初始条件组合与投掷成绩对照

由表7 可见，刘启臻的出手角度为31.7°，接近国外优秀男子标枪运动员的平均出手角度32°，攻角为-4.1°，出手初速度为 28.58m/s，出手初速度比国内其他两名运动员的都大，攻角比国内其他两名运动员的都小，所以其投掷成绩较佳，但低于国外优秀男子标枪运动员平均掷成绩。因此，每个运动员的个人风格只有被标枪在空中飞行时的“有效投掷条件”所制约，在长期的运动实践中，通过科学的训练，渐渐形成与出手速度较为匹配的其他各初始出手条件，才能够获得更加优异的成绩。

初速度是影响标枪飞行远度的必要条件。从运动力学的角度来说，标枪运动员要想提高投掷初速度，必须增大作用于标枪上的力，延长力作用于标枪的距离，同时缩短力作用于标枪的时间。而由于人的臂长有限，力作用于标枪的距离有一定的局限性，而增大作用于标枪上的力和缩短力作用于标枪的时间却有较大的潜力[18-19]。因此，标枪运动员要想提高投掷成绩，应从全面提高自身身体素质和缩短力作用于标枪的时间等方面着手。标枪运动员出手时的“鞭打”动作是增大作用于标枪上的力和缩短力作用于标枪的时间的主要因素[20]。

从运动生物力学角度来说，运动员在投掷标枪时，出手角度的选择,要以能够使标枪获得最大的出手速度为前提条件。由于人体的解剖结构和最后用力的动作特点，运动员在投掷标枪出手角度较小时，有利于将全身肌肉力量作用于标枪上，能够产生较大的出手速度[21]。研究分析表明，世界优秀男子标枪运动员的最佳出手角度一般为32°左右[22]。

从有利于发挥空气动力效率来说，最佳攻角的选择应考虑合理的升阻比问题。研究分析表明，随着攻角的增加，空气对标枪的升力和阻力都会增大，但当攻角增大到一定值时，阻力会很大，而升力却不再增大了。当攻角绝对值在（0—10）°范围内时，阻力增加的较为缓慢，攻角的绝对值超过10°以后，阻力随攻角的增加而迅速增大[23，会大幅度降低标枪向前飞行的速度，减少标枪的水平飞行距离，所以攻角绝对值不能够太大。当出手角度较大时，与之对应的最佳初始攻角较小；当出手角度减小时，与之对应的最佳初始攻角随之增大，在一定条件下形成了二者之间的最佳组合。当出手角度为32°时，与之对应的最佳初始攻角为-3°[24]。

初始俯仰角速度是标枪出手时绕其横轴转动的角速度，当运动员作用在标枪上力的方向与标枪的纵轴线方向不一致时，就会使标枪产生初始俯仰角速度。上述研究分析表明，当初始攻角在（0—6）°范围内时，标枪的飞行远度有所增大，这是因为适宜的初始俯仰角速度可以阻止初始攻角过大，从而避免标枪飞行时出现过于抬头现象。如果俯仰角速度过大时，标枪就出现较大的抬头或低头现象，导致标枪的飞行攻角出现变化，进而导致升阻比的变化并对标枪的飞行远度产生很大影响。当初始俯仰角速度在（-20—20）°/s 范围内变化时，标枪的飞行远度会相相差（15—20）m[25]。当最佳初始攻角为-3°时，与之对应的最佳初始俯仰角速度为-10°/s。

初始偏航角是标枪初速度的方向与标枪纵轴在地面的投影线之间的夹角。偏航角的大小直接决定标枪出手后在空中的飞行轨迹，进而影响其飞行远度[26]。研究分析表明，就是一些世界级的优秀运动员，在掷标枪时，为了追求较大的出手初速度，通常采用大幅度转体，以便产生更大的爆发力，当转体角度稍有控制不到位时，常会引起标枪出现初始偏航角。如果能把偏航角控制在（0—18）°范围内时，标枪的飞行远度下降幅度会较小些。当其绝对值超过20°时，飞行远度会有大幅度下降[27]。因此，运动员在最后用力时,不仅要发挥最大的出手速度,而且也应该控制好用力方向。

标枪旋转速度的大小和方向是由运动员投掷标枪时手指拨动标枪力的大小与方向所决定的。研究分析表明，由于标枪是一个细长体，其绕横轴与绕纵轴之间的转动惯量值相差很大，即使标枪绕其纵轴的旋转速度为零时，由于气动力使得标枪绕其纵轴旋转力矩很小，标枪在飞行过程中也不会出现翻转现象，而旋转本身并不能够提高标枪的飞行远度。如果在投掷标枪出手时，追求过高的初始旋转速度，反而会使标枪的初速度下降，而减小标枪在空中飞行的距离[28]。显然，试图通过提高标枪旋转速度来提高飞行远度的做法是不可取的。