MIMU/GPS 紧组合系统在车辆导航中的应用

◎刘新源

（三门峡职业技术学院智能制造学院，河南三门峡 472000）

车辆方便了人们的出行，导航在车辆的重要性也日益凸显，研究人员对其研究也越来越多。目前对车辆的导航使用最多的是全球定位系统（GPS），其能够提供高精度的位置、速度，但是在高楼区、山区、隧道等环境下，GPS 信号容易失效导致不能定位[1,2]。研究人员对组合导航在车辆上应用开始研究，如卫星导航/地图匹配组合[3]、卫星导航/MIMU 组合[4]等方式来补充GPS 信号失效时对车辆的导航。卫星导航/微惯性组合导航又分为松散组合和紧组合两种方式[5]。松散组合仅仅利用GPS 提供的位置和速度信息对MIMU系统进行校正，而微惯导系统不能反过来对GPS进行修正且需要四颗卫星同步观测。紧组合是利用GPS 的多普勒速度和载波相位等原始信息与MIMU 系统进行组合导航，两者的信息可以相互校正且在极端的情况下有一颗卫星信息即可进行导航解算，利用两种导航误差的独立性、不相关性能够使组合导航输出更高精度的导航信息。笔者采用MIMU/GPS 系统紧组合方式组合导航，设计利用GPS 接收机接收卫星信号的原始信息（多普勒速度和载波相位）与微观性系统提供的姿态信息、电子罗盘提供的姿态信息进行组合导航，建立紧组合导航系统的状态方程和量测方程，利用卡尔曼滤波输出车辆的姿态信息。

1 GPS 载波相位和多普勒速度的数学模式

紧组合导航系统需要利用GPS 接收机接收卫星信号的伪距、多普勒速度和载波相位信息，因此要首先建立其数学模型，以供紧组合系统的量测方程使用。首先根据GPS 载波相位测量的基本原理[6]，得到GPS 卫星到接收机的伪距ρ，其线性化的载波相位方程为：

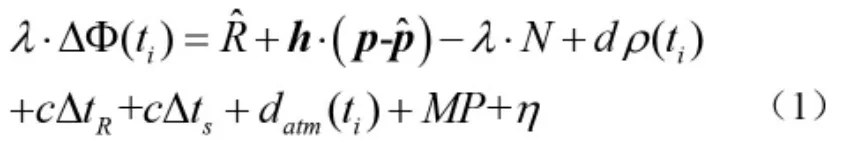
其中方程式是在地球坐标系下计算求得的，c 是卫星位置到估测接收机位置的距离；h 是从卫星到GPS 接收机的单位向量；P 是接收机的真实位置是估测得到的接收机位；λ 是载波波长；N 是载波的整周数dP（ti）是广播轨道偏差，△ts是卫星钟差、△tR是接收机R 钟差、datm（ti）是载波信号传播的大气层延迟、MP 是多路径效应，η 是由噪声等误差源引起的量测噪声误差[7]。

根据GPS 测速基本原理得到多普勒测速方程[5]，其线性化的测速方程为：

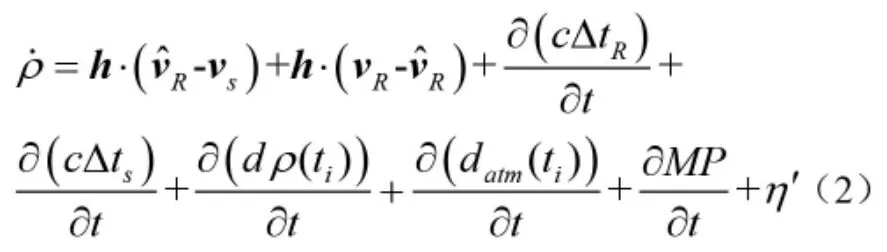
其中方程式是在地球坐标系下计算得到的，Vs是 GPS 卫星真实的速度；是估测得到的GPS 接收机的速度；VR是GPS 接收机的真实速度是对时间相关误差量求导；

利用两台接收机接收到的数据并结合式（1）和式（2）分别得到接收机1、接收机2 的GPS 载波相位方程和多普勒测速方程，并对其进行作差处理，得到站际单差的相位差方程和速度差方程，即为：

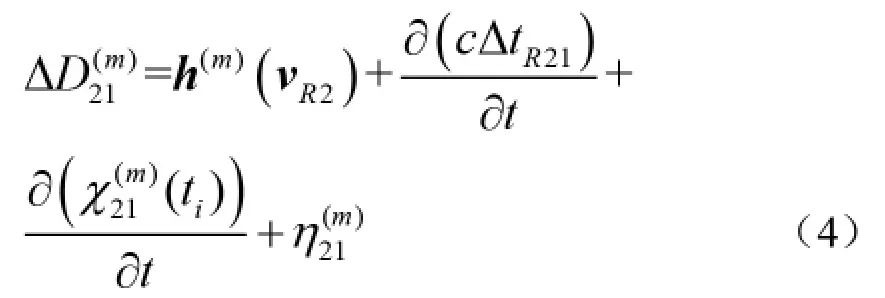
其中，χ（ti）=datm（ti）+MP 是大气层延迟与多路径效应误差之和，再进一步的求差，能够将其忽略掉。上标（m）是该量为卫星m 的量，下标1或2 表示的是接收机l 或2 的量。

在得到的站际单差的基础上，进行星际单差。根据式（3）与式（4）将卫星 m 和 q 卫星的站际单差的相位方程和速度方程分别作差可以得到站际、星际双差的相位差方程和速度差方程，即为：

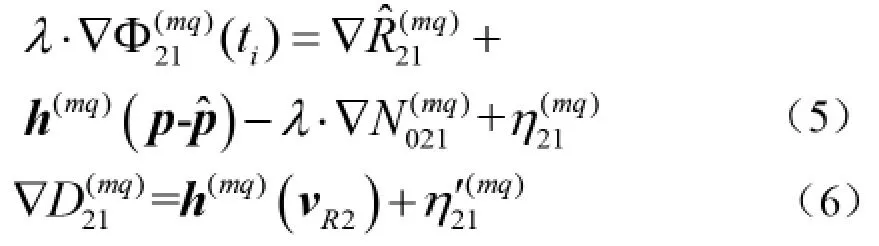
2 紧组合系统的状态方程和量测方程

笔者设计的紧组合导航系统是利用GPS 接收机提供的多普勒速度和载波相位原始信息与微观性系统提供的姿态信息、电子罗盘提供的航向信息进行组合导航，因此选取微观性系统的平台失准角、速度误差、位置误差、惯性器件误差以及电子罗盘误差作为状态变量，并采用东北天坐标系，则其紧组合系统的状态方可以表示为：

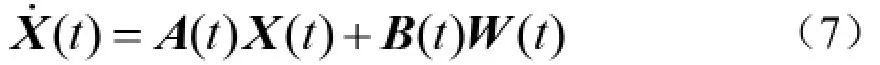
其中，X 为18 维的状态变量，即

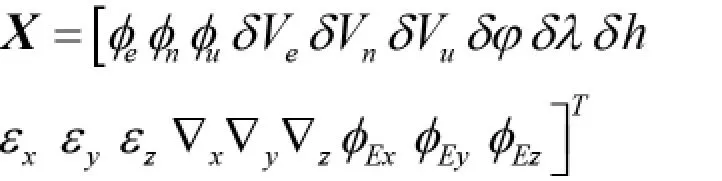
其中下标e、n、u 表示的是东北天向，即东北天地理坐标系，Φe、Φn、Φu是东北天地理坐标系的平台失准角，δVe、δVn、δVu是东北天地理坐标系的速度误差，δφ、δλ、δh是东北天地理坐标系的纬度、经度和高度位置误差，εx、εy、εz是东北天地理坐标系的各轴向上的陀螺漂移，△x、△y、△z是东北天地理坐标系的各轴向上的加速度计零偏，ΦEx、ΦEy、ΦEz是东北天地理坐标系的电子罗盘的测量误差。

W 为系统的噪声向量，即

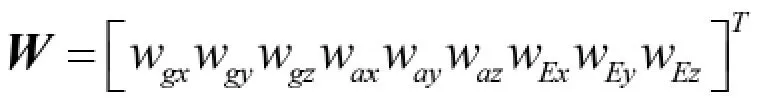
A 为18×18 维的系统状态转移矩阵，其形式为：

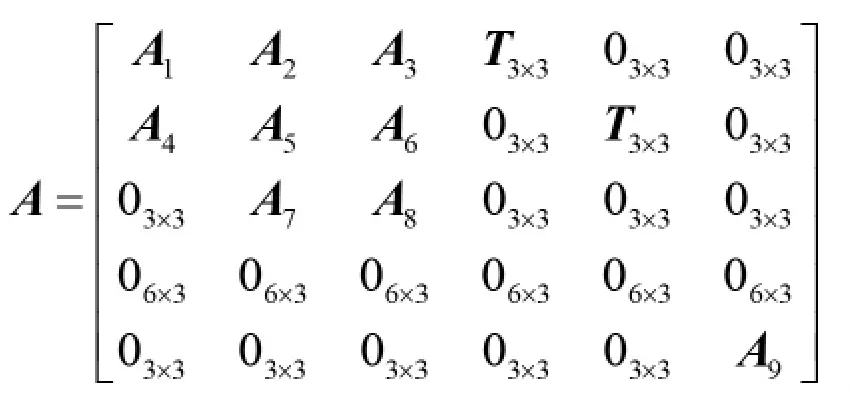
B 为18×9 维的系统噪声矩阵，其形式为：

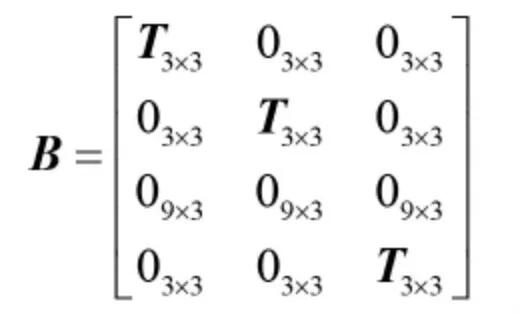
其中，T3×3为捷联矩阵 Tbn，A1，A2，A3，A4，A5，A6，A7，A8，A9的具体表达式如下：

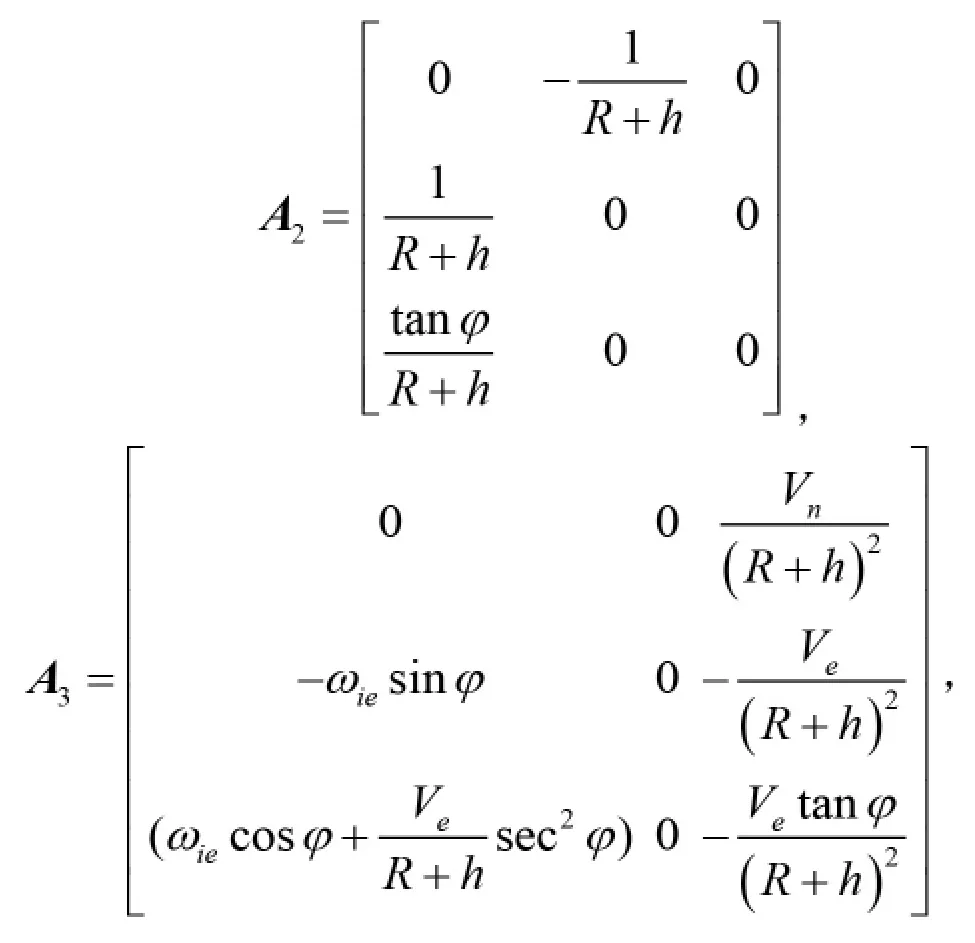
笔者设计的紧组合导航系统的量测方程由两部分组成：一是微观性系统提供的姿态误差与电子罗盘提供的姿态误差之间的差值作为组合导航的量测量，二是利用GPS 接收机接收卫星信号的原始信息，多普勒速度与载波相位数学模型作为量测量。首先是建立微观性系统提供的姿态误差与电子罗盘提供的姿态误差之间的差值作为量测量[8]，可表示为：

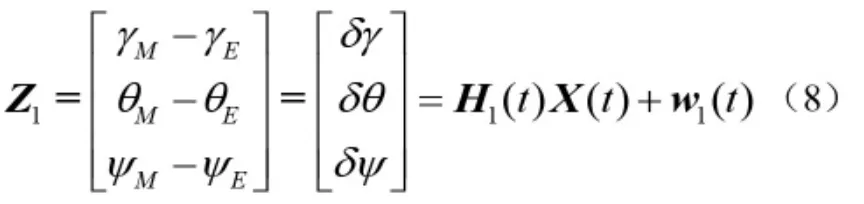
其中 δγ、δθ、δψ 是横摇角、纵摇角和航向角的误差角，γM、θM、ψM是微惯性输出的横摇角、纵摇角和航向角，γE、θE、ψE是电子罗盘输出的横摇角、纵摇角和航向角。

X 为18 维的状态变量，W 为三维的量测噪声矩阵，H 为量测矩阵，其表达形式为：

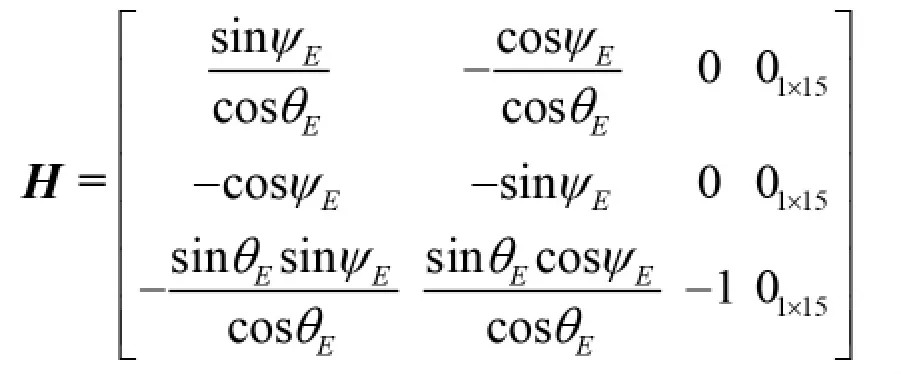
建立利用GPS 接收机提供原始信息的量测量，根据笔者在第2 部分得到的式（5），是在地球坐标系下的载波相位双差方程，将其转换到导航坐标系下[9]，并整理改写为：

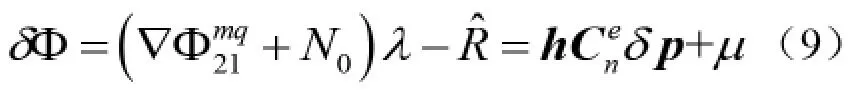
同理，根据笔者在第2 部分得到的式（6），将其转换到导航坐标系下[9]，并整理改写为：

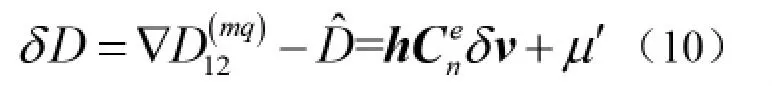
根据前面的介绍，式（9）和式（10）的组合即为GPS 部分量测方程：

其中，W2为GPS 部分的量测噪声矩阵， 可以表示为 W2=[μ μ']T，H2为量测矩阵，其表达形式为：

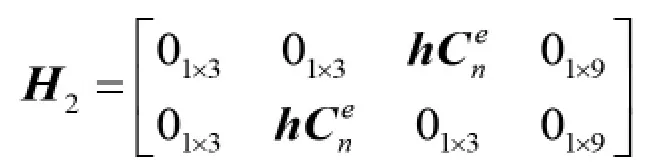
将上述两部分的量测方程合并，得到微惯性/电子罗盘/GPS 紧组合系统的量测方程，即为：

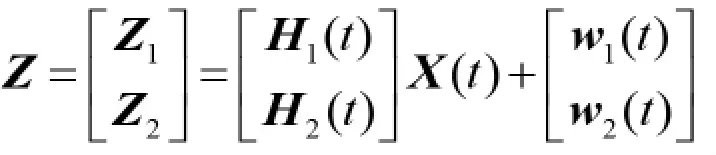
3 试验与分析

为了验证笔者设计的紧组合系统性能，进行跑车试验。试验过程采用实验室购置的法国iXSEA 公司生产的PHINS 捷联惯导系统作为参考基准，在试验车上固定安装好MTi-G 航姿系统和PHINS 捷联惯导系统，同时利用自编软件实现串口为100Hz 的采样频率，同步采集各个系统输出数据。主GPS 天线处于固定位置，为了更好接受卫星信号，移动GPS 天线位于靠车窗位置。

完成跑车试验数据采集之后，截取1 小时车载试验数据，利用微惯性/GPS/电子罗盘紧组合算法进行离线处理，所绘制姿态估计曲线与PHINS 捷联惯导系统输出的参考姿态曲线对比图如图1 所示，两者之间的姿态误差曲线如图2所示。

根据图1 可以看出，笔者提出MIMU/GPS 紧组合系统的组合姿态与捷联惯导参考的姿态之间误差很小，可以说明本算法跟踪效果良好，图2 所示的姿态误差曲线直接描述了本系统算法的误差：纵横摇误差为±0.2°，航向误差则为±2°。综上分析可知，笔者设计的紧组合系统算法对车辆的姿态具有较好的精度。

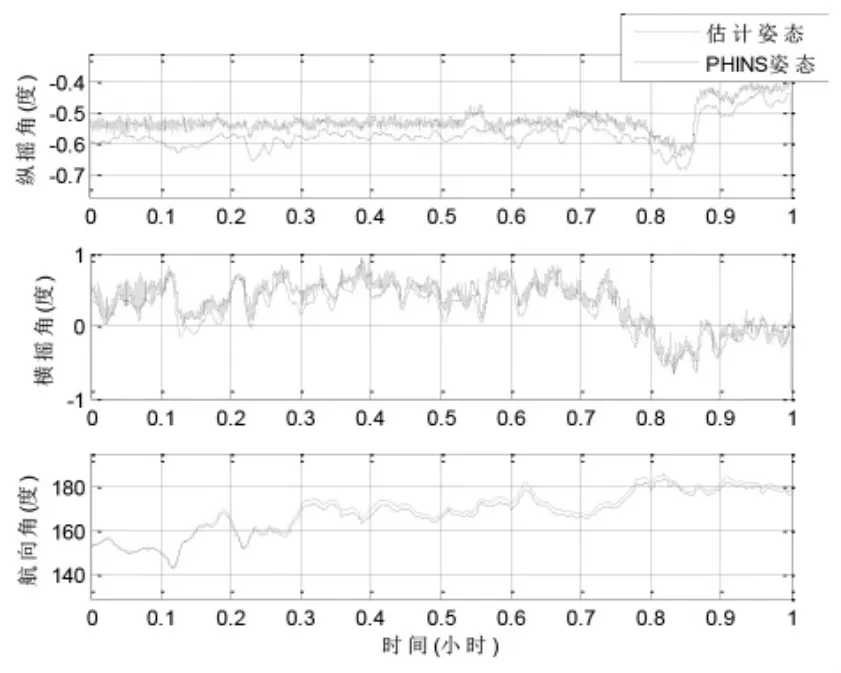
图1 紧组合导航系统输出姿态与PHINS 惯导输出姿态对比图

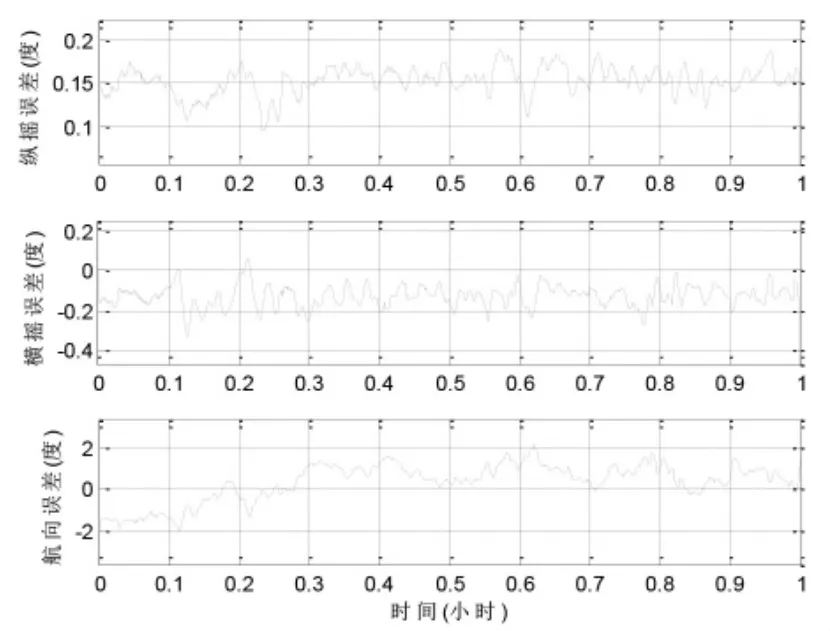
图2 紧组合导航系统输出姿态误差曲线图

4 结语

笔者设计了在车辆导航中的MIMU/GPS 紧组合导航系统。详细推导了GPS 系统的载波相位双差方程和速度双差方程的数学模型，在此基础上建立紧组合导航系统的状态方程和量测方程，并利用卡尔曼滤波输出车辆导航的姿态信息。最后，通过车载采集各个系统输出数据，系统算法离线处理的实验证明了该组合方案有效地控制了车辆姿态的误差，车辆导航精度得到提高。