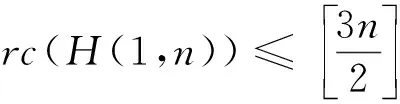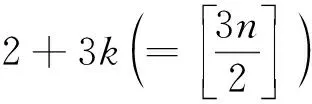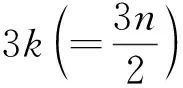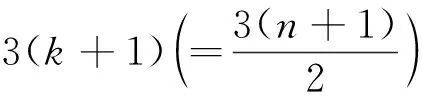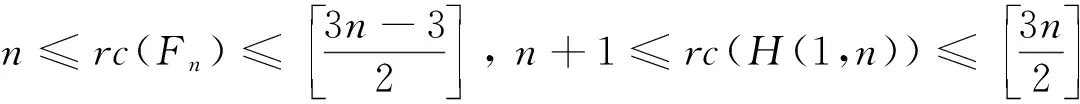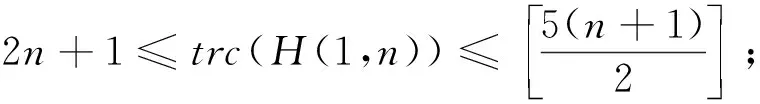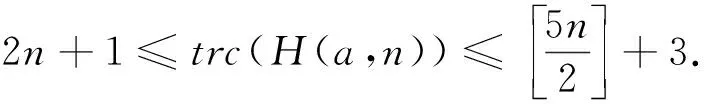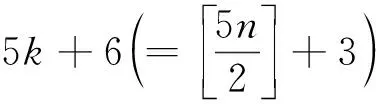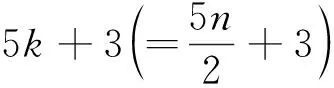(广义)Farey图的彩虹连通性

刘素娟, 王林林

(1.天津科技大学 人工智能学院, 天津 300071; 2.中国矿业大学 数学学院, 江苏 徐州 221116)

0 引言

彩虹连通数是一个自然的组合概念, 在信息的安全传输等领域有重要的应用[1-2].彩虹连通数的研究得到了众多专家学者的关注[3-7].本文讨论了Farey图和广义Farey图的彩虹顶点连通数, 彩虹连通数和完全彩虹连通数，其中所考虑的图均为有限无向简单图, 未定义的术语和概念参见[8].

彩虹连通数的概念推广包括强彩虹连通数[9], 彩虹k-连通数[10], 彩虹顶点连通数[11], 完全彩虹连通数[12]等.顶点着色图中的所有内部顶点都染不同颜色的路称为彩虹路.顶点着色图G是彩虹顶点连通的, 如果G中的任意两个不同顶点之间都有一条彩虹路相连.定义图G的彩虹顶点连通数, 记为rvc(G).对于图G=(V,E),c:V∪E→{1,2,…，k}是G的一个完全着色.图G中的所有边和内部顶点都染不同颜色的路称为完全彩虹路.若G中任意两个不同顶点之间都有一条完全彩虹路相连, 则称图G是完全彩虹连通的,c为G的完全彩虹着色.定义图G的完全彩虹连通数为其完全彩虹着色所需的最少的颜色数, 记为trc(G).显然,rvc(G)≥diam(G)-1,trc(G)≥2diam(G)-1.

MATULA[13]等人于1979年根据Farey序列提出了Farey图的概念.

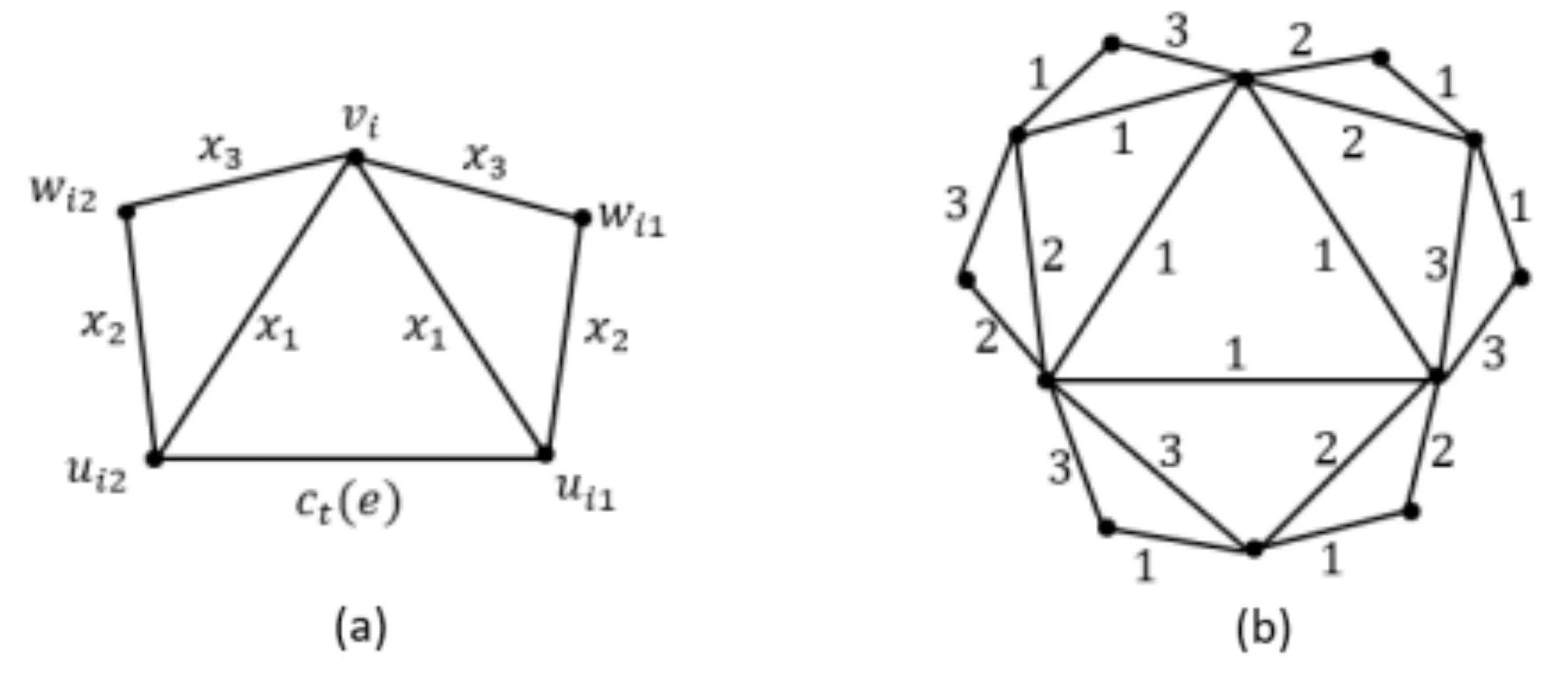
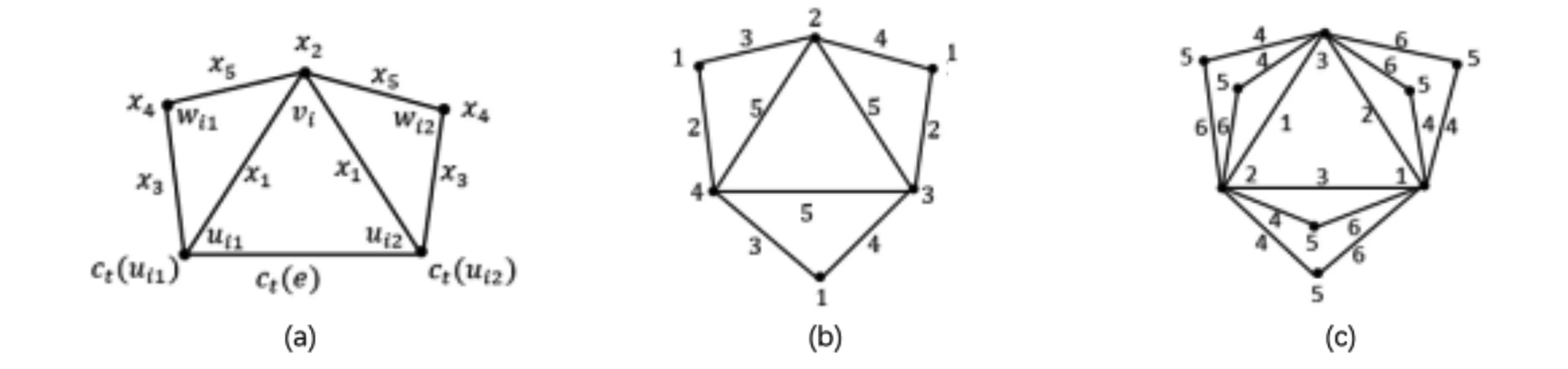
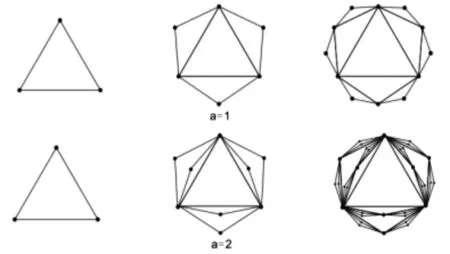
对于图G中的顶点v,NG(v)表示v的邻点构成的集合.对于路P=v0v1…vk(k≥1),称顶点v0,vk为路P的两个端点; 记viPvj=vivi+1…vj(0≤i

定义1 Farey图Fn(n≥0)是通过下面的迭代方法得到的.

1)F0是一条边;

2) 当n≥1时,Fn通过对Fn-1中第n-1步新增的每一条边添加一个顶点, 并将这个顶点与这条边的两端点相连得到.

Farey图F0,F1，F2，F3和F4.如图1所示.记V(Fn)=V0∪V1∪…∪Vn,E(Fn)=E0∪E1∪…∪En其中V0=V(F0),E0=E(F0),Vi=V(Fi)V(Fi-1),Ei=E(Fi)E(Fi-1),即Vi和Ei分别为Fn在第i步新增的顶点集合和边集合.ZHANG[14]等人研究了Farey图的阶数, 边数, 度分布, 直径, 平均距离等拓扑性质, 并证明了Farey图是一个与某些复杂系统相关的网络模型.接下来给出广义Farey图H(a,n)的概念.

图1 Farey

定义2 对于正整数a和非负整数n, 定义广义Farey图H(a,n)如下:

1)H(a,0)=K3, 即H(a,0)是3个顶点的完全图;

2) 当n≥1时,H(a,n)通过对H(a,n-1)中在n-1步新增的每一条边添加a个顶点, 并将这a个顶点与这条边的两端点相连.结果如下图所示.

图2给出了a=1,2,n=0,1,2时的广义Farey图.记V(H(a,n))=V0∪V1∪…∪Vn,E(H(a,n))=E0∪E1∪…∪En, 其中V0=V(H(a,0)),E0=E(H(a,0)),Vi=V(H(a,i))V(H(a,i-1)),Ei=E(H(a,i))E(H(a,i-1)), 即Vi和Ei分别是H(a,n)在第i步新增的顶点集合和边集合.

图2 广义Farey图H(a,n)

1 主要结论

首先给出Farey图和广义Farey图的直径.

命题1[14]对于Farey图Fn,diam(Fn)=n(n≥1), 其中diam(Fn)是图Fn的直径.

命题2 对于广义Farey图H(a,n)(a≥1,n≥0),diam(H(a,n))=n+1, 其中diam(H(a,n))是图H(a,n)的直径.

证明当a=1时,Fn+1是H(1,n)的一个顶点诱导子图, 由Fn和H(1,n)的定义可得,diam(H(1,n))=diam(Fn+1)=n+1.当a≥2时, 可以验证diam(H(a,n))=diam(H(1,n))=n+1.

下面讨论Farey图和广义Farey图的彩虹顶点连通数.首先给出严格彩虹顶点着色的定义.

定义3设c是图G的一个顶点着色.若G中路P是彩虹路, 且两端点的颜色与内部顶点的颜色也不同, 则称路P是严格彩虹路.若G中的任意两个顶点之间都有一条严格彩虹路相连, 则称c为图C的严格彩虹顶点着色.

显然, 严格彩虹顶点着色也是一个彩虹顶点着色.在严格彩虹路中, 两端点的颜色可以相同.

定理1对于广义Farey图H(a,n)(a≥1,n≥0),n≤rvc(H(a,n))≤n+2.

证明由rvc(G)≥diam(G)-1和diam(H(a,n))=n+1可得rvc(H(a,n))≥n.为了证明rvc(H(a,n))≤n+2, 只需构造H(a,n)的一个n+2种颜色的彩虹顶点着色.当n=0,1时, 可以验证rvc(H(a,n))=n成立.

下面通过归纳法证明:n≥2时, 存在H(a,n)的n+2种颜色的严格彩虹顶点着色cn.

定义H(a,1)的顶点着色c1如下: 首先将H(a,0)的3个顶点分别用颜色1,2,3染色; 然后将V1中的顶点用1,2,3中的与其两个邻点颜色不同颜色染色.可以验证,c1是H(a,1)的3种颜色的相邻顶点染不同颜色的严格彩虹顶点着色.假设ci-1是H(a,i-1)(2≤i≤n)的i+1种颜色的相邻顶点染不同颜色的严格彩虹顶点着色.定义H(a,i)的i+2种颜色的顶点着色ci如下: 若v∈V(H(a,i-1)),ci(v)=ci-1(v);若v∈Vi,ci(v)=i+2, 其中i+2是新颜色.显然,ci是H(a,i)的i+2种颜色的相邻顶点染不同颜色的顶点着色.

接下来证明ci是严格彩虹顶点着色.

设u,v是H(a,i)中两个顶点.

1) 当u,v∈V(H(a,i-1))时, 由ci的定义可得, 在H(a,i-1)中存在一条u,v之间的严格彩虹路；

2) 当u∈Vi,v∈V(H(a,i-1))时, 记u在H(a,i-1)中的两个邻点为u′,u″；

3) 当v∈{u′,u″}时,u,v相邻,显然存在u,v之间的严格彩虹路；

4) 当v∉{u′,u″}时, 因为相邻的顶点u′,u″染不同的颜色,u′或u″ (不妨设为u′)与v的颜色不同, 即ci(u′)≠ci(v).在H(a,i-1)中存在一条u′和v之间的所有顶点都染不同颜色的严格彩虹路P.从而, 路uu′Pv是u,v之间的严格彩虹路.当u,v∈vi时, 设u,v在H(a,i-1)中的邻点分别为u′,u″和v′,v″.当v′∈{u′,u″}时,uv′v是u,v之间的严格彩虹路.当v′∉{u′,u″}时, 由前面的证明可知, 在H(a,i-1)中存在一条u′或u″(不妨设为u′) 到v′的所有顶点都染不同颜色的严格彩虹路P.从而, 路uu′Pv′v是u,v之间的严格彩虹路.因此,ci是H(a,i)的严格彩虹顶点着色.

综上,cn是H(a,n)的n+2种颜色的彩虹顶点着色, 即rvc(H(a,n))≤n+2.

Farey图Fn是广义Farey图H(1,n-1)的一个顶点诱导子图, 在定理1中构造了H(1,n-1)的彩虹顶点着色cn-1.定义Fn的顶点着色c.对于v∈V(Fn)⊆V(H(1,n-1)),cv=cn-1(v).由定理1的证明可知,c是Fn的n+1种颜色的彩虹顶点着色.结合命题 1,可得下面的推论.

推论1对于Farey图Fn(n≥1), 有n-1≤rvc(Fn)≤n+1成立.

下面讨论Farey图和广义Farey图的彩虹连通数.

首先考虑n=2k+1(k≥1)的情况.由rc(H(1,1))=2得到，存在H(1,1)的一个2种颜色的彩虹边着色c0.假设H(1,1+2t)(0≤t

定义H(1,3+2t)的边着色ct+1为: 若e∈E(H(1,1+2t)),ct+1(e)=ct(e);ct+1(ui1vi)=ct+1(ui2vi)=x1;ct+1(ui1wi1)=ct+1(ui2wi2)=x2;ct+1(wi1vi)=ct+1(wi2vi)=x3, 其中x1,x2,x3是新颜色.图3(a)给出了新添加边的着色方法.显然, 边着色ct+1使用了2+3(t+1)种颜色.

接下来证明ct+1是H(1,3+2t)的一个彩虹边着色.

任取H(1,3+2t)中的两个顶点u,v.当u,v∈V(H(1,1+2t))时,在H(1,1+2t)中存在一条u,v之间的彩虹路.

1) 当u∈V(H(1,1+2t)),v∈V2+2t∪V3+2t(不妨设v∈{vi,wi1,wi2})时, 则vui1P1u或vui2P2u(其中P1和P2分别是H(1,1+2t)中的从u到ui1和ui2的彩虹路) 是u,v之间的一条彩虹路；

2) 当u,v∈V2+2t∪V3+2t且u,v∈{vi,wi1,wi2}时, 则在顶点集合{ui1,ui2,vi,wi1,wi2}诱导的子图中存在u,v之间的一条彩虹路.

3) 考虑u,v∈V2+2t∪V3+2t且u∈{vi,wi1,wi2},v∈{vj,wj1,wj2}(i≠j)的情况.令P1,P2分别表示H(1,1+2t)中的ui1到uj1和ui2到uj2的彩虹路； 由ct+1的定义可得, 当u=wi1时,wi1ui1P1uj1vj,wi1ui1P1uj1wj1和wi1ui1P1uj1vjwj2都是彩虹路,即u,v之间存在一条彩虹路.当u=wi2或u=vi时, 可类似证明u,v之间存在一条彩虹路.

图3 (a) H(1,3+2t)的新增边着色； (b) H(1,2)的彩虹边着色

下面讨论Farey图和广义Farey图的完全彩虹连通数.首先给出严格完全彩虹着色的概念.

定义4设c是图G的一个完全着色.若G中的路P是完全彩虹路, 且两端点的颜色与内部顶点和边的颜色都不同, 则称路P是一条严格完全彩虹路.若G中的任意两个顶点之间都有一条严格完全彩虹路相连, 则称完全着色c为G的严格完全彩虹着色.

显然, 严格完全彩虹着色也是一个完全彩虹着色.在严格完全彩虹路中, 两端点的颜色可能相同.

首先考虑n=2k(k≥1)的情况.构造H(1,2i)(0≤i≤k)的一个5i+3种颜色的完全着色ci.令H(1,0)=v1v2v3v1, 即H(1,0)是一个3长圈.定义H(1,0)的3种颜色的完全着色c0为:c0(v1)=c0(v2v3)=1,c0(v2)=c0(v1v3)=2,c0(v3)=c0(v1v2)=3.可以验证,c0是H(1,0)的3种颜色的相邻顶点染不同颜色的严格完全彩虹着色.假设ct是H(1,2t)(0≤t

在H(1,2t+2)中,记E2t={ei=ui1ui2|1≤i≤3·22t} ,V2t+1={vi|1≤i≤3·22t},V2t+2={wi1,wi2|1≤i≤3·22t}, 在第2t+1和2t+2步新增的2长路分别为Pi=ui1viui2,Pij=uijwijvi,1≤i≤3·22t,j=1,2.

定义H(1,2t+2)的完全着色ct+1:

1) 若e∈E(H(1,2t)),ct+1(e)=ct(e);

2) 若v∈V(H(1,2t)),ct+1(v)=ct(v);

3) 若e∈E2t+1,ct+1(e)=x1;

4) 若v∈V2t+1,ct+1(v)=x2;

路Pij=uijwijvi(1≤i≤3·22t,j=1,2)的内部顶点和边依次用x3,x4,x5染色, 其中xi(1≤i≤5)是新颜色.新增的边和顶点的染色方法如图4(a)所示.显然,ct+1是H(1,2t+2)的5(t+1)+3种颜色的相邻顶点染不同颜色的完全着色.

接下来证明ct+1是严格完全彩虹着色.

设u,v是H(1,2t+2)中两个顶点.

图4 (a) H(1,2t+2)新增边的顶点着色； (b) H(1,1)的完全着色； (c) H(2,1)的完全着色

关于Farey图和广义Farey图的完全彩虹连通数, 有下面的结论.

定理3对于Farey图Fn和广义Farey图H(a,n), 有下面的结论成立:

下面讨论a≥2时的H(a,n)的完全彩虹连通数.由diam(H(a,n))=n+1可得,rc(H(a,n))≥2n+1.

考虑n=2k+1(k≥0)的情况.设V(H(a,0))={v1,v2,v3}.定义H(a,1)的6种颜色的严格完全彩虹着色c1如下：

c1(v1)=c1(v2v3),c1(v2)=c1(v1v3)=x2,c1(v3)=c1(v1v2)=x3;

对于H(a,1)在第1步新增的2长的路P=vivvj(其中vi,vj∈V(H(a,0))),c1(viv)=4,c1(v)=5,c1(vvj)=6,其中4, 5, 6是新颜色.H(2,1)的完全着色c1如图4(c)所示.可以验证c1是H(a,1)的6种颜色的严格完全彩虹着色, 且满足条件: 长度为1的路的边和顶点都染不同的颜色.假设ct是H(a,2t+1)的一个5t+6种颜色的严格完全彩虹着色, 且满足条件: 长度为1的路的边和顶点都染不同的颜色.

定义H(a,2t+3)的完全着色ct+1如下:

若e∈E(H(a,2t+1)),ct+1(e)=ct(e);

若v∈V(H(a,2t+1)),ct+1(v)=ct(v);

若e∈E2t+2,ct+1(e)=x1;

若v∈V2t+2,ct+1(v)=x2;

对于H(a,2t+3)在第2t+3步新增的2长的路P=vivvj(其中vi∈V(H(a,2t+1)),vj∈V2t+2),ct+1(viv)=x3,ct+1(v)=x4,ct+1(vvj)=x5, 其中xi(1≤i≤5)是新颜色.显然,ct+1是H(1,2t+3)的5(t+1)+6种颜色的完全着色, 且满足条件: 长度为1的路的边和顶点都染不同的颜色.

当1≤n≤3时, 可以验证rvc(Fn)=diam(Fn)-1,trc(Fn)=diam(Fn),rc(Fn)=2diam(Fn)-1.下面给出一个猜想.

猜想1对于Farey图Fn(n≥1), 有rvc(Fn)=diam(Fn)-1;trc(Fn)=diam(Fn);rc(Fn)=2diam(Fn)-1成立.