多步骤船舶轨迹聚类方法研究与实现∗

蒋 通 崔良中 周 钢 张社国

（1.海军工程大学电子工程学院 武汉 430033）（2.中国人民解放军92682部队 湛江 524000）

1 引言

船舶自动识别系统是船舶航行安全和海上监视的关键，在船舶行为模式分析［1］和海上交通规律挖掘［2］的研究与应用中受到了广泛关注。对AIS船舶轨迹数据开展聚类分析研究，可以跟踪与预测船舶航行轨迹，检测与识别船舶异常行为［3］，从而为航运规划和海事监管等工作开展提供决策支持和科学依据。目前，国内外学者对于船舶轨迹聚类的研究主要从以下三个方面展开。

在研究对象方面，21世纪初Knorr等人以整条航迹为聚类的对象，使用位置、方向和速度等三个维度组成的序列来表示每个位置点，运用传统距离函数来计算轨迹之间距离并对航迹进行聚类。而Lee等［4］将整条航迹划分成子航迹，考虑航迹的结构性特征，来计算子航迹段之间的相似性。此后肖潇等［5］将航迹方向变化较大的点作为整条航迹的分割点，对分割后的子航迹进行聚类。

在相似性度量方面，大多数是基于距离进行计算，诸如欧几里得距离、hausdorff距离和最长公共子序列距离等。然而，航迹的速度、方向等特征都应当被考虑在内。牟军敏等［6］基于hausdorff距离，设计自动选取尺度参数的相似度度量函数，构造相似度矩阵；雷鹏［7］将包含多个特征的结构化距离进行归一化，避免由于各项特征的取值范围差别较大而造成的实验误差。

在算法选择方面，目前常用的航迹聚类算法主要包括基于密度［8～9］（DBSCAN、OPTICS）、基于统计学（GMM、KDE）和基于网格（CLIQUE、STING）的轨迹聚类算法等。其中，DBSCAN算法因其能够发现任意形状的簇类而被广泛改进和应用。江玉玲等［10］采用离散Frechet距离作为轨迹相似度度量，利用类似DBSCAN算法对轨迹段进行聚类，得出船舶运动典型轨迹；PALLOTTA等［11］采用增量DBSCAN算法对AIS船舶轨迹数据中的转向点进行聚类，在此基础上分析船舶的交通流模式。

然而，原始AIS数据是如何一步步变成可以为我们所用的有效信息，相关系统完整的研究较少。为解决这一问题，本文在对AIS数据进行预处理后，提出一种多步骤船舶轨迹聚类方法，主要包括轨迹压缩、轨迹点匹配与距离相似性度量和轨迹聚类等三部分，并利用真实AIS数据进行实例验证。

2 数据预处理

原始AIS数据预处理过程如图1所示。

图1 AIS数据预处理流程图

AIS报告种类包括船位报告、基地台报告和信道管理等13种，长度从168～1192比特数不等。对AIS数据进行预处理首先需要对其各个组成部分进行剖析，将信息进行解码处理，才能转化成我们需要的水上移动通信业务标识码（MMSI）、IMO编号、船长和船宽和船舶类型等静态信息，以及船舶位置、对地航速、对地航向和航行状态等动态信息。

AIS数据经过解析后主要存在三个方面的数据质量问题：1）重复（连续两行数据完全一致）；2）缺失（如某一行数据中某个属性数据为空）；3）错误（某些数据明显与客观事实不符，如实际航向超出0～3599、实际航速超出0～1022等）。这些数据都应该去除，否则会对实验结果产生不可忽视的影响。

每一条AIS数据中记录着大量信息，在本文对船舶轨迹聚类的研究中，我们只需提取MMSI、时刻、实际航速、经度、纬度和实际航向等六种属性信息，这样可以有效提高后续计算效率。

为方便后续研究的开展，一般需要先对数据进行无量纲化处理，这样表征不同属性的各数据之间才有可比性。数据规范化的常用方法主要包括z分数规范化、正则化、小数定标规范化和最小-最大规范化。根据AIS航迹数据的特点，本文选用最小-最大规范化。

假设minA和maxA分别为属性A的最小值和最大值。最小-最大规范化通过计算：

把A的值vi映射到区间［0，1］中的v'i。最小-最大规范化既可以放大某些标准差较小的特征之间的差异，又能够保留原始数据中由标准差所反映的潜在权重关系，因此被广泛应用。

对AIS数据进行预处理后的结果及对部分数据进行规范化的结果如图2所示。

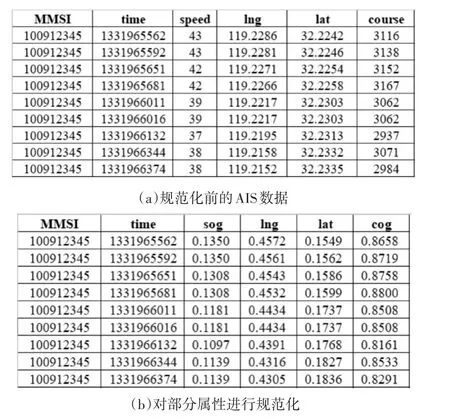
图2 规范化前后的AIS数据对比

3 多步骤船舶轨迹聚类方法

完成对AIS数据的预处理后，本文提出多步骤船舶轨迹聚类方法［12］，主要由轨迹压缩、轨迹点匹配与距离相似性度量和轨迹聚类等三部分组成。完整流程如图3所示。

图3 多步骤船舶轨迹聚类方法

3.1 轨迹压缩

每一条轨迹都可以看做是一条不规则曲线，在对轨迹数字化时，要对曲线进行采样，即在曲线上取有限个点，将其变为折线，并且能够在一定程度上保持原有的形状。经典算法步骤如下。

运用经典 Douglas-Peucker（DP）［13］算法压缩轨迹时，只考虑了轨迹点的经度和纬度，而忽略了航向和航速对压缩结果的影响，往往会导致不能将“转折点”或“变速点”保留下来。因此，本文在经典DP算法的基础上进行改进，通过查阅相关文献资料以及咨询航海领域专业人士，保留符合以下条件中至少一条的轨迹点：

也即保留航向或航速变化较大的点。

以经度为横坐标、纬度为纵坐标，经改进的DP轨迹压缩算法处理前后的轨迹对比如图4所示。原始轨迹包括73个轨迹点，压缩后轨迹包括58个轨迹点，轨迹点减少的同时能够基本保持原有形状。

图4 轨迹压缩前后对比

3.2 轨迹点匹配和距离相似性度量

在某一区域、某一时间段内的所有AIS航迹数据中，不同航迹包含的轨迹点数量往往不同，而且，仅依据经纬度作为衡量轨迹间距离的指标往往是片面的，因此如何更全面、更准确地对不同轨迹的轨迹点进行匹配以及轨迹间距离相似性如何度量成为目前研究的热点问题。

每一条航迹都可以看作是由相邻轨迹点连接而成的子航迹段组成，我们采用动态时间规整算法（DTW）［14］对不同航迹之间的轨迹点进行匹配，保证每条航迹的任一轨迹点在另一条航迹当中都能找到与之匹配的轨迹点，把它们之间的等效认为是以此轨迹点为起点的子航迹段之间的“距离”。算法的思想是使用迭代的方法求出任意两条航迹的匹配路径，使得“距离”最小。

假设有两条轨迹为Traj1和Traj2，T1i表示第一条轨迹的第i个轨迹点，T2j表示第二条轨迹的第j个轨迹点，DTW(i,j)表示Traj1的前i个轨迹点组成的轨迹和Traj2的前j个轨迹点组成的轨迹之间的最小“距离”。那么：

不同轨迹之间的结构化距离中除了几何距离外，还包括由于航向和航速的差异而导致的“距离”［15］，我们也需要对此进行度量。假设m和n是任意两条不同轨迹上的点迹，可以用四维向量来描述其特征，以点m为例：

其中，lat表示纬度，lng表示经度，cog表示航向，sog表示航速。以点迹m为例，将sogm在两个方向轴进行水平和垂直投影分解为Vm//和Vm⊥两个分量：

对sogn进行同样分解，则不同轨迹上的点迹之间的速度差异可以表示为

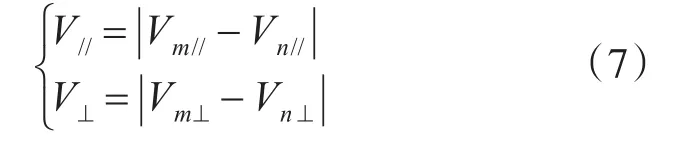
同理，将两轨迹点之间的几何距离d(m,n)分解为d//和d⊥两个分量，由于地球为近似的椭球体，可以用如式（8）进行计算：

其中，C表示两点与球心连线的夹角，Rc为地球的平均半径。

那么m、n两点之间地结构化距离为

上式中，μi表示各“距离”所占权重，需满足条件：μi≥0,i=1,2,3,4且∑μi=1。

3.3 轨迹聚类

在应用比较广泛的几类轨迹聚类算法中，DBSCAN算法是一种有代表性的基于密度的无监督聚类算法。它将簇定义为密度相连的点的最大集合，在无须事先设定簇的个数前提下，能够发现任意形状和大小的簇，而AIS数据具有噪声点多、轨迹不确定的特性，应用DBSCAN算法能够获得较好的聚类效果。

应用DBSCAN算法进行轨迹聚类的结果取决于邻域半径参数ε和邻域密度阈值MinPts的确定。本文对DBSCAN算法的改进正是体现在这两个参数的选取方法上。

聚类的目的是将样本数据集尽可能地聚合成簇。邻域密度MinPts一定的情况下，邻域半径ε过大会导致簇之间区分度很小，ε过小会导致得到的簇较少，而噪声点较多；邻域半径ε一定的情况下，邻域密度MinPts过大会导致噪声点较多，MinPts过小会导致聚成的簇数较多，不能实现聚类的目的。本文采用基于核密度估计和噪声数据量变化的方法来确定合适的邻域半径参数ε和邻域密度阈值MinPts。

核密度估计（KDE）是一种用于估计概率密度函数的非参数方法，x1,x2,…,xn为独立同分布F的n个样本点，其概率密度函数为f，则核密度估计可表示为

其中，K(.)为核函数，h为一个平滑参数，称作带宽或窗口，Kh(.)为缩放核函数。

高斯核函数是比较常用的核函数，对于噪音数据有着较好的抗干扰能力，其数学形式如下：

其参数决定了函数作用范围，因此其性能对参数十分敏感。为降低函数对参数的依赖性，本文选用指数函数，其数学形式如下：

将式（13）、（15）两式联立，可得到概率密度函数表达式为

邻域密度阈值MinPts∈[1 ,n]，其中n为样本总数，根据上述方法可确定MinPts不同取值下对应的邻域半径参数ε。

噪声数据量的变化可以用来衡量聚类的效果。随着邻域密度阈值MinPts的增大，噪声数据量逐渐减少，且速度呈现出由慢到快再到慢的趋势，部分学者［16］基于此认为使得噪声数据量变化率最大的MinPts最为合适，然后这并不能保证将样本数据集尽可能地聚合成簇，因此本文对此进行改进，假设g为邻域密度阈值MinPts到噪声数据量的一个映射：

最合适的MinPts应满足以下要求：

其中，n为样本总数。从上式中可以看出，MinPts的取值应保证噪声数据不超过样本总数的5%，这样可以取得更好的聚类效果。

4 实验验证与分析

4.1 实验准备

本文基于Python语言编写程序并进行了实验。选取2013年1月某连续10h内在长江入海口河段部分水域（119.0°E～119.5°E、32.2°N～32.3°N）测得的115098条AIS数据作为样本。利用DP算法压缩轨迹时的阈值dMax取0.01，距离结构化度量中的权重参数μ1、μ2、μ3、μ4均取 0.25，改进的基于DBSCAN算法的轨迹聚类算法中的两个重要参数ε取52.5，MinPts取20。

4.2 实验结果与分析

对AIS数据进行预处理后，筛选出至少包含100个轨迹点的194条航迹，运用本文提出的多步骤船舶估计聚类方法进行聚类，并与文献［15］提出的基于行为特征相似度的船舶轨迹聚类方法进行对比，结果如表2所示。

从表1中可以看出，本文方法在获取更多簇数的情况下，噪声数据反而较少，且通过下文的主航道提取可以得出本文方法更加合理的结论。

表1 轨迹聚类结果

利用Python作图，以经度为横坐标、以纬度为纵坐标，分别将每一类航迹进行展示，如图5所示。

从图5中可以看出，船舶在该水域航行的轨迹主要有三条，以类别二为代表的轨迹主要位于所选区域的西南一侧，大致航向为东北-东南，并且转向过程基本在119.10°E～119.15°E完成；以类别三为代表的轨迹主要位于所选区域的东南一侧，大致航向为东北-正东，转向角度小于“类别一”；而以类别一为代表的轨迹显著特点是航向的多次改变。

为能更好地表示聚类结果，利用Matlab作图，取每一类轨迹的均值，得到平均轨迹，也可以理解为船舶在该水域航行的三条主要航道，如图5所示。

图5 轨迹聚类结果示意图

图6 长江口某水域主航道示意图

值得注意的是，样本数据中有四条航迹没有被聚到任何簇中，可以认为它们是“异常”的，往往代表着船舶比较特殊的行为模式，不同于海上目标一般的行动规律。通过整合和比较可知，每一条轨迹都会出现一段基本与y轴平行的部分，而且4条轨迹的航速最大航速不超过7节（图7），航行过程中基本保持在3节～5节（图8）。通过对该水域实际情况的调查，得知可能是从事拖带、引航、水下作业等活动的特殊船舶的轨迹。

图7 异常轨迹位置变化

图8 异常轨迹航速变化

5 结语

本文针对目前AIS船舶轨迹聚类过程不够系统完整的问题，首先对原始AIS数据进行预处理，提出主要包括轨迹压缩、子轨迹匹配、相似性度量和轨迹聚类等三部分的多步骤船舶轨迹聚类方法，并以长江入海口河段部分水域的真实数据进行实验验证，结果表明该方法不仅可以找出船舶在该水域航行的主要航道，而且能够发现异常轨迹的存在，在航道规划和海事监管方面有一定的应用意义，对AIS船舶轨迹聚类的研究有一定的参考价值。