表贴式多相分数槽绕组电机的电感分析∗

戴雅婷 李东臻 邱 原

（海军工程大学 武汉 430033）

1 引言

无刷直流电机由于结构和驱动控制方法简单，控制方式类似于传统的直流电机，因此在中小功率传动场合得到了广泛的应用［1］。大容量传动场合可采用多相分数槽绕组降低每相容量，同时提高转矩密度和减小电流谐波［2］。合适的电机极、槽数的分数槽绕组，还能够有效地抑制无刷直流电机的转矩脉动［3］。

电机电感参数对于建立电机数学模型、分析电机性能与研究控制策略十分重要。多相分数槽绕组电机不能沿用传统三相整数槽电机的传统电感计算方法，这是由于［4～8］：

1）不同于正弦波供电的交流电机，电机的方波气隙磁密均参与产生有效电磁转矩，因此相绕组磁通的各次谐波应计入主电感，而不是单独计算谐波漏感；

2）相绕组通入的电流为近似方波，不同于交流电机的正弦波；

3）电机若采用表贴式磁极，等效气隙大，主电感与漏电感较接近；

4）各相绕组的互感不按空间位置角的余弦规律变化，需按照各相的绕组函数重新推导，而分数槽绕组的相互关系更加复杂。

一般来说，电感的计算可以分为由基本元件磁势分析出发的磁路方法［9～10］、采用等效面电流的解析磁场方法［11～12］或有限元法。有限元计算方法精度高，能够考虑铁芯的饱和，但计算时间长、物理意义也不明确，难以获得自感与各相互感的关系。解析磁场方法虽有明确的物理意义，但推导十分复杂。因此本文从解析磁路出发，借鉴绕组函数的思路，推导多相分数槽绕组无刷直流电机的通用电感计算公式。

2 电感计算的基本方法

分析对象为表贴式永磁电机，并作如下假设。

1）假设铁芯材料的磁导率为无穷大，忽略铁芯材料的饱和与损耗；

2）沿圆周方向气隙均匀，各处磁导相同，永磁体的气隙处磁密波形为理想方波；

3）气隙磁场的正方向规定为由转子外表面进入定子为内表面。

由电感L的含义可知，其为磁链ψ与产生该磁链的电流i之比为

磁链是磁通Φ与所交链线圈匝数N的乘积，即：

根据磁路欧姆定律，磁通可由磁动势（MMF）与磁路磁导的乘积求得

因此电感计算的关键在于求得该电流在磁路上所产生的磁动势F与磁路处的磁导λ。对于电机绕组的电感计算，由于假设中忽略了铁芯材料的磁压降，因此主要问题在于计算沿气隙圆周的磁动势及气隙处磁导。

气隙磁动势的计算可借鉴绕组函数的思想，不用考虑整数槽绕组与分数槽绕组的区别，由安培环路定理得到其分布函数，从而得到通用的电感计算公式。

3 电枢反应自感的计算

首先计算一相绕组通入电流im后在气隙产生的磁动势。

分数槽结构的相绕组由分布于多个单元电机、同相位的线圈组成，考虑到单元电机之间完全对称的绕组分布，气隙磁动势的分布完全一致，于是可以将单元电机作为对象分析相绕组产生的磁动势。

在单元电机内，一个节距为y（按槽数计算）、匝数为Nc的线圈嵌放在定子槽内（见图1）。

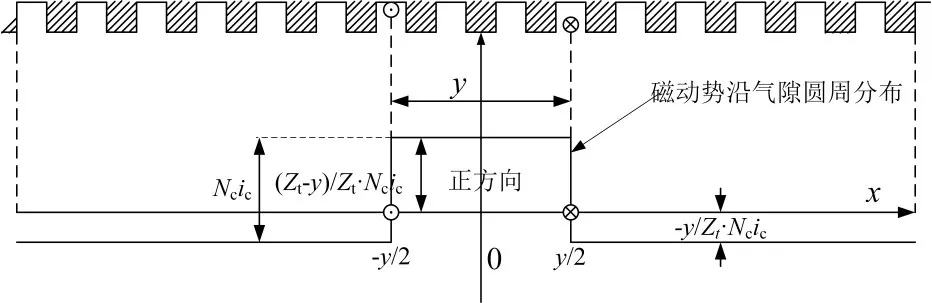
图1 绕组元件在气隙中产生的磁动势

当线圈通入电流ic时，它将在在气隙圆周上产生一个闭合磁场，考虑到正方向的规定，该定子磁动势沿气隙圆周将按图示分布。由磁路的安培环路定理可知，线圈所产生的磁动势为磁力线所包围的总电流，它的幅值就为

由磁通连续性定理，该线圈磁动势所产生的磁通进入定子轭部与从定子轭部穿出的磁通量必然相等，但由于线圈的跨距不是半个单元电机圆周，因此两个方向磁通通路的面积不同，磁动势沿气隙圆周的分布必然也不同，它与通路面积成反比。由于给位置铁芯轴向长度一致，通路面积与各自磁路的圆周长度决定。以绕组槽数为单位计算，定义x为沿圆周方向的槽数，原点位于线圈的轴线。由以上分析知道沿圆周的气隙磁动势的表达式为

式中Zt为单元电机的槽数。在得到单个线圈在气隙产生的磁动势后下一步需要计算气隙处磁通路径的磁导，气隙磁导计算式为

式中δef是考虑了永磁体厚度的等效气隙长度，Ag是与绕组交链的气隙磁通路径面积，其表达式分别为

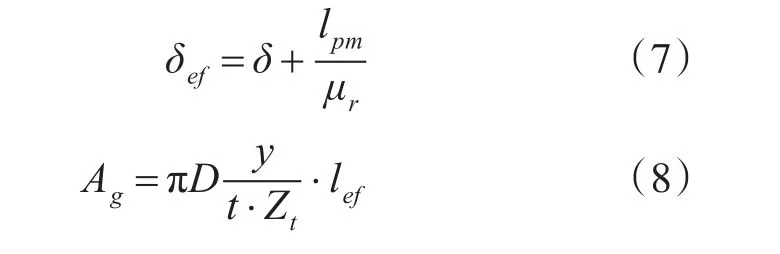
式中δ为气隙长度；lpm为永磁体厚度；μr为永磁体的相对磁导率；t为单元电机数；D为气隙圆周处的直径；lef为定子铁芯的有效长度。

在得到沿气隙分布的磁动势表达式与气隙磁导后，在线圈跨距y个槽内累加得到与线圈交链的磁通，为

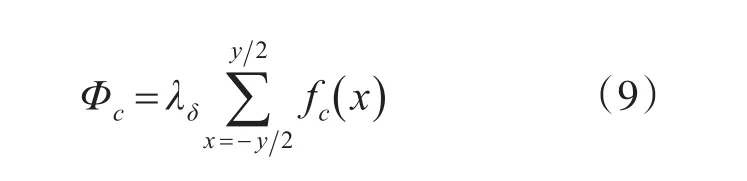
4 电枢反应互感的计算

对于多相绕组结构，根据两相绕组的相互位置，它们的互感计算需要分为三种情况。下面计算第k相对第j相绕组的互感。两相绕组相距的槽数为|k-j|。

4.1 | k-j|＜y的情况

|k-j|＜y时两相绕组位置的相互关系如图2，k相线圈在气隙中产生的磁通与j相线圈交链的部分既有正向，又有反向。

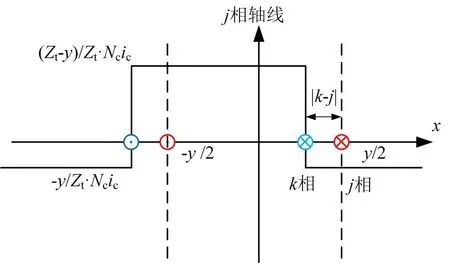
图2 |k-j|＜y时两线圈相互位置

此时k相线圈在气隙中产生的磁动势分为

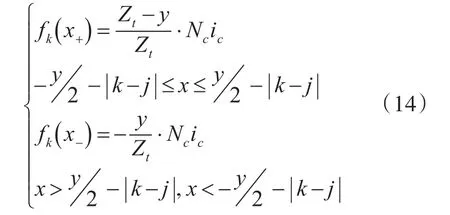
下面需要分别计算磁通正向部分与反向部分的气隙处磁导，它们的区别仅在于磁通路径沿圆周方向的长度不同，分别为

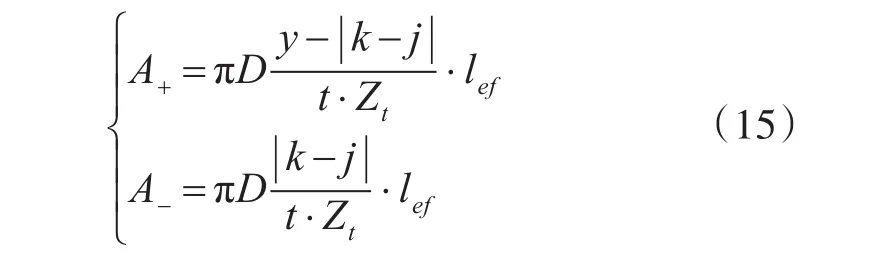
按照与自感相同的计算方法可以得到两部分的气隙磁导，λ+和λ-。在线圈跨距y个槽内累加，得到k相线圈在气隙中产生的磁通与j相线圈交链的部分之和。

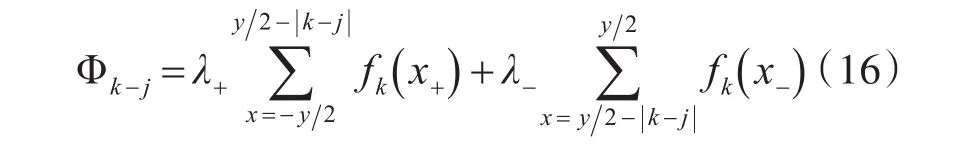
4.2 y≤| k-j|≤z-y的情况

y≤| k-j|≤z-y时两相绕组位置的相互关系如图3，此时k相线圈在气隙中产生的磁通与j相线圈交链的部分全为反向。

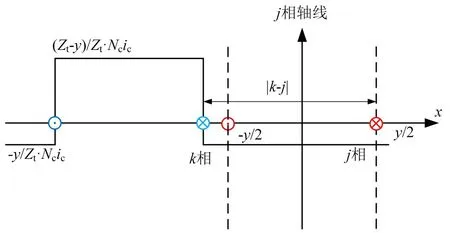
图3 y≤| k-j|≤z-y时两线圈相互位置

4.3 | k-j|＞z-y的情况

|k-j|＞z-y时两相绕组位置的相互关系如图4所示，k相线圈在气隙中产生的磁通与j相线圈交链的部分同样既有正向，又有反向。

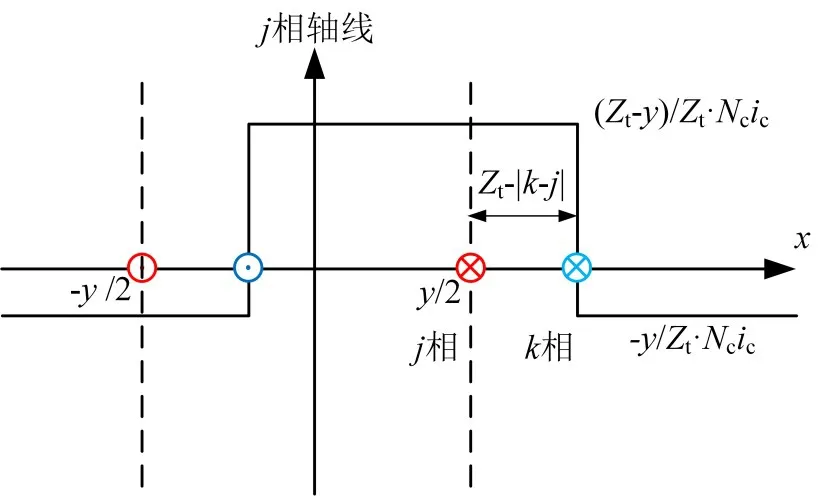
图4 | k-j|＞z-y时两线圈相互位置

此时k相线圈在气隙中产生的磁动势分别为

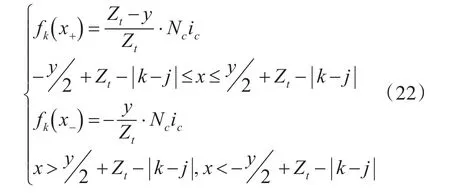
下面需要分别计算磁通正向部分与反向部分的气隙处磁导，它们的区别仅在于磁通路径沿圆周方向的长度不同，分别为按照与自感相同的计算方法可以得到两部分的气隙磁导，λ+和λ-。在线圈跨距y个槽内累加，得到k相线圈在气隙中产生的磁通与j相线圈交链的部分之和。

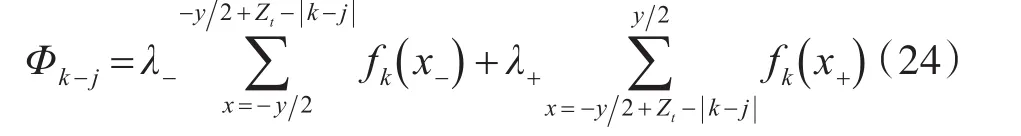
在线圈跨距y个槽内累加，得到k相线圈在气隙中产生的磁通与j相线圈交链的部分之和。

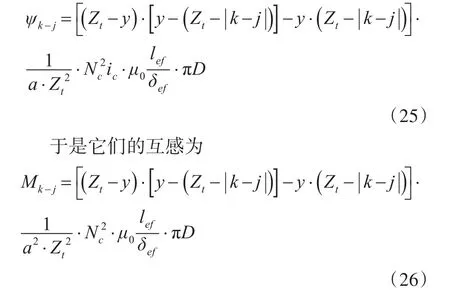
将式（18）、（21）、（26）三式统一起来便得到两相绕组的互感完整表达式。

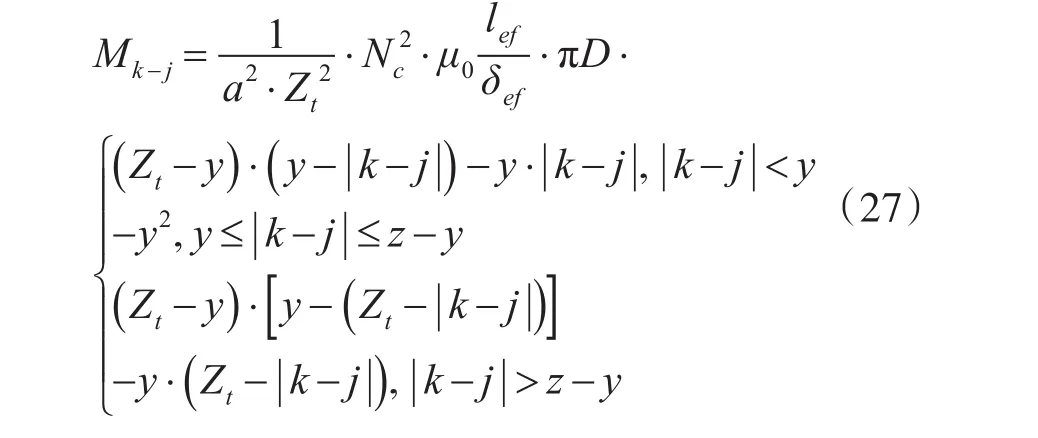
5 漏电感与总电感的计算

电机漏电感是由不穿过气隙的磁通引起的，由于分数槽绕组特别是节距y较小时的电机端部绕组很短，端部漏电感含量较小，因此电机漏电感的主要成分是槽漏电感。槽漏电感的计算方法与传统交流电流类似，这里不再赘述。

需要注意的是，槽漏感既存在与一相绕组的自感中，也存在满足一定关系的两相绕组互感中，如图5所示。一相绕组的槽漏电感是相绕组线圈的原边与副边元件经槽底、槽内空间、槽口闭合的漏磁场分量，定义为Lls；当两相绕组相距的槽数恰好等于相绕组的跨距时，它们有元件边同槽，磁链会通过定子齿槽相互交链，于是两相绕组有互感作用，定义为Llm。

图5 槽漏电感的磁路

6 算例

以一台8极、46槽、23相无刷直流电机为例，通过有限元仿真验证电机电感参数的计算结果。该电机由两个4极23槽单元电机组成，两单元电机间的线圈串联成一相绕组，电机的具体参数如表1所示。

表1 算例参数

由电机的结构参数代入上文推导的电感计算表达式，能够计算电枢得到相绕组的主自感Lm，一相的槽漏电感Lls，两相互交链的槽漏电感Llm及各相间的互感Mtotal_k-j。解析计算公式的一项优势是能够得到电机各电感参数间的关系，例如当|k-j|<6时，各相间的互感为

利用ANSYS Maxwell 16.0建立如图6的电机有限元仿真模型验证电感的计算结果，有限元仿真采用静态求解器。

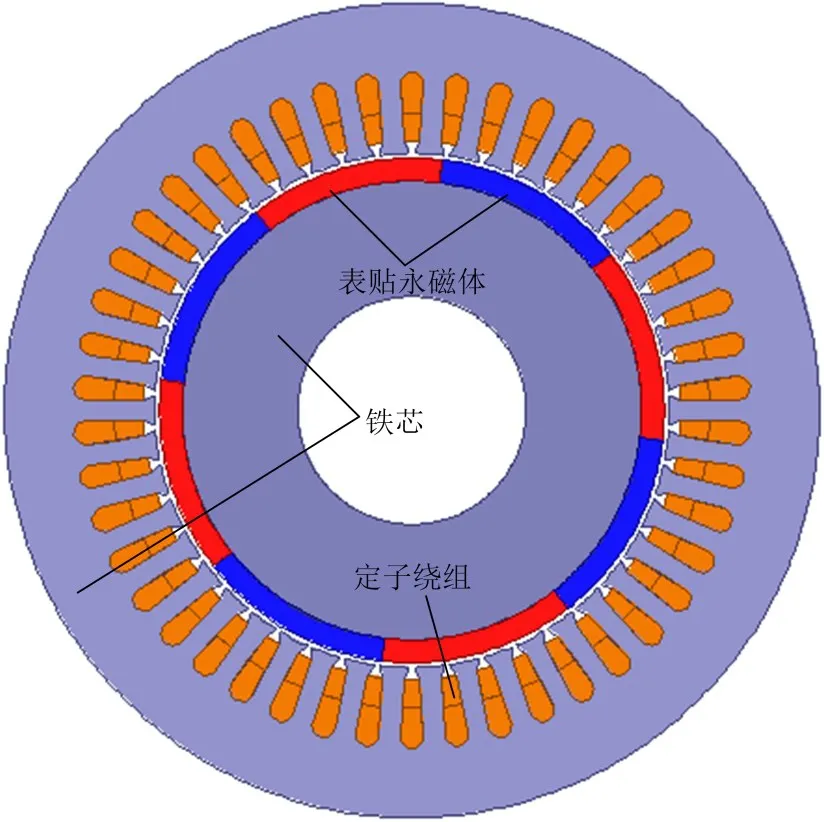
图6 电感计算的有限元模型

解析方法与有限元仿真的部分结果如表2，由于互感矩阵具有对称性，因此所给出的结果已经能够验证计算结果。电感计算的误差在7%以内，满足工程需求，若考虑定子开齿及饱和的影响，计算精度将进一步提高。这种计算方法最大的好处是能够获得电机各自感之间的关系，从而非常方便编程计算多相电机中数目众多的电感参数。

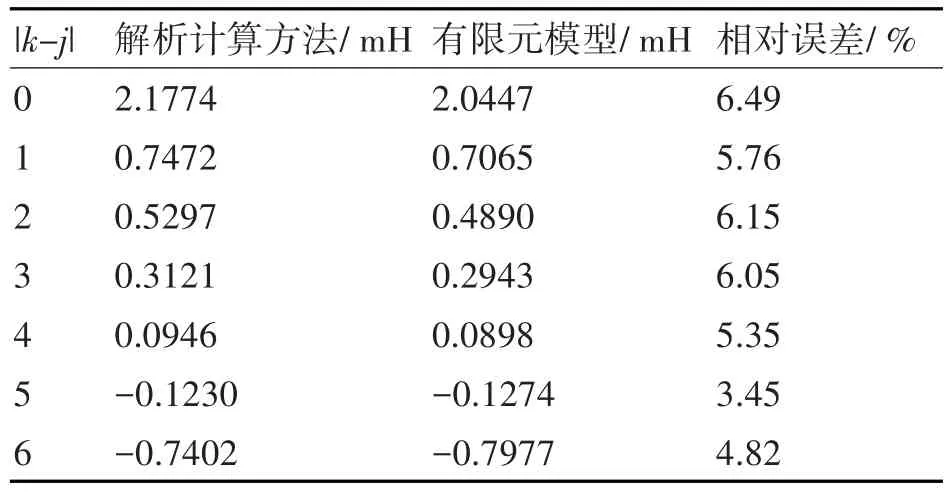
表2 电感计算结果

7 结语

本文针对表贴式多相分数槽绕组无刷直流电机，借鉴绕组函数的思路，由磁路方法解析推导了通用的电感计算公式，其计算过程简单，物理意义清晰，并通过有限元仿真验证了计算结果，验证结果表明满足工程精度需求。该解析公式能够得到电机自感与各相互感间的关系，因此能够大大减少多相绕组电感参数的数目，有利于编程计算和多相电机数学模型的建立。

本文所推导的通用计算公式适用于不同结构的分数槽绕组，例如当y=1时可以计算集中绕组结构的电感。由于整数槽结构属于分数槽绕组的一种特殊情况，因此同样可以用来计算多相整数槽结构的各相电感。