小学生代数思维培养探析

商红领/北京市海淀区中关村第一小学副校长

商红领

小学代数学习主要内容包括用字母表示数和正反比例。用字母表示数参与到“等量关系”和“变化规律”的表示和运算中，等量关系和变化规律就可以刻画一类事件，体现着字母表示一般性。

方程以及与方程有关的函数，是基础教育阶段数学教学最为核心的内容，小学的字母表示数和正反比例作为代数思维培养的起始，其重要性可见一斑。

长期以来，小学生早期代数思维培养一直是老师非常关心的问题。我们知道，算术和代数作为两种不用的思维方式，它们有着本质的不同。算术思维是一种程序性思维，是由已知推出未知，指向问题的答案，而代数思维更加关注问题本身的内部结构，是一种关系性思维和结构性思维，将未知与已知放在同等地位上，实现对一般性表示、运算和推理的认识和理解。用字母表示数量关系和结构中的等价关系，是帮助学生从算术思维走向代数思维的关键，同时也是学生学习的难点。这种“难”，体现在思维方式的“转变”。之所以是“转变”，是因为在之前的学习中算术思维的主导地位，已经使算术思维成为学生的思维习惯。从算术到代数，不但是思维方式的转变，同时也是一种思维习惯的转变，这种转变就更加不易了。

如何帮助学生建立代数思维呢？如何帮助学生顺利地从算术思维过渡到代数思维呢？笔者从实践探索中总结了以下策略：

保护关系性思维、结构性思维

（一）用好教材资源，充分理解等号的等价关系

东北师范大学史宁中教授形象地描述，“方程就是讲了两个故事，这两个故事说的是同一件事，是等价的，我们把两个故事用等号连接起来，就是方程”。可见方程的核心是建立等价关系，而算术思维，将等号作为指向结果的过程，因此，让学生正确认识等号的功能非常重要。等号代表等价关系，在教材中有很多的体现，例如：

上图是北师大版一年级教材中的一道思考题。在这个题目中等号代表的不是要算出结果是多少，而是表达等号两边是等价的关系。教学中，我们可以把重点放在解题的思考过程上。例如，引导学生思考，把这八个数分成四组，每组两个数的和是相等的，应该如何分组呢？学生要结合数的特征，最大的和最小的凑在一起，第二大的和第二小的放在一起……这样的思考过程中，是利用数的特征，思考相等关系，等号是表示两边的算式相等，而不是算出结果是9。我们还可以将题目进行一点变化，如下图：

经过改造后的题目答案不唯一，可以引导学生对比思考，使学生意识到，只要每组中两个数的和相等就是正确的，强化等号表示的等价关系。

再如，小学四则运算中的第二个基本关系——乘法。下图是北师大版四年级下册教材的内容。学生在解决问题过程中，不是真的要通过计算找到哪两个数相乘等于4.48或者等于1.015，本质上是寻找1.6×2.8=□×□；0.29×3.5=□×□。学生是在利用关系解决问题，同时感受等号代表的等价关系。

如上的例题，在教材中不胜枚举，都是非常重要的、能帮助学生理解、深化等号的等价关系的重要资源。

等号的结构性关系有一个突出的呈现就是教材中的运算定律。如下图：

在惯有的思维中，学习运算律最重要的作用是简便运算。因此，老师们非常注重引导学生观察算式中数的特征，恰当地选择运算定律进行简便运算。实际上运算定律的学习过程，本身也是进一步认识、理解等号表示等价关系和运算律本身结构的重要途径。甚至在解题过程中，也要适当打开思路，为学生创造更多感悟等价关系和结构的机会。例如下面的例题：

从题目引导的思路上看，主要目的是引导学生关注简便运算，如果我们把目光放得更加长远，这样的题目可以放得更开，后面两个题目的答案是不唯一的，每一个答案都有加法交换律和结合律做保障，同时强调这些都是等价关系，在若干答案中，有些答案在获取结果上有一定优势。这样的活动在分析和说理过程中，对交换律和结合律有了充分的应用，利于学生理解，同时强化了等价关系和运算律本身的结构性，在对比中也可以突出根据数的特征运用运算定律可以达到简算的目的。

（二）允许学生的思维顺序，呵护正向思维

在常态教学中，我们经常会遇到这样的问题，学生的算式写“错”了，回答的问题结果却是正确的。这种“错”指的是所求的结果没有写到等号后面。将答案写在等号后面，实际上就是算术思维的一种显著表现（在算术思维中等号指向的是运算结果）。例如以下例题：

学生在解决这个问题的过程中，一般会出现两种情况。一种是5-4=1（个）、5-3=2（个），还差1个杯子2个勺子，这是我们所期望的学生表现。另外一种是4+1=5（个）、3+2=5（个），还差1个杯子2个勺子，这就是上面提到的算式写“错”了，特别是当提问的方式是：需要增加几个杯子？增加几个勺子？写成这样的“错误”算式的同学会更多一些。

教师如何看待学生的第二种情况，直接反映了我们头脑中对代数思维的认识。如果我们站在代数思维的角度看第二种情况，你会发现，学生的算式是建立在一个等量关系基础上的数学表达，只是学生还不会使用代数的表达方式。这个等量关系就是“现有的杯子+增加的杯子=5”“现有的勺子+增加的勺子=5”。我们需要帮助学生解决的是如何进行正确表达，而不是纠正学生算式的错误，不能简单粗暴地要求将答案放到等号后面。

站在算术思维和代数思维的视角看待我们学生的两种方法都是正确的，这样的教学落在每个学生的认知中两种方法都是对的。这个时候，在学生头脑中，算术法和代数法是并存的，可以减少后继学习中对代数法的不适应，减少思维方式和思维习惯的扭转阻力。

（三）创造更多使用关系性思维解决问题的机会

有了上面教材中的示例，有了学生表现的分析，我们可以沿着这样的思路给学生创造更多使用关系性思维解决问题的机会。例如以下例题：

学生在解决问题的过程中，观察数的变化，利用关系来解决问题。在解决□+△=10；3+〇=▽两个问题时，鼓励学生找到所有答案，感受符号的代表性，以及在等量关系中变化的依存关系，渗透函数思想。

整体把握教材，关注单元主题

列方程解题的优势是在解决相对复杂的问题时，将未知量放在和已知量同等地位来思考问题，可以降低思维的负担。例如，在北师大版五年级下册教材中安排的《邮票张数》和《相遇问题》两个内容。《邮票张数》解决的是“和倍问题”中求一倍量的问题，《相遇问题》是一个求相遇时间的问题。

以相遇问题为例，相信很多老师都会在课堂上给学生独立思考解决“相遇问题”的时间，在学生的交流中充分理解“相遇问题”的数量关系，进而学会解题。

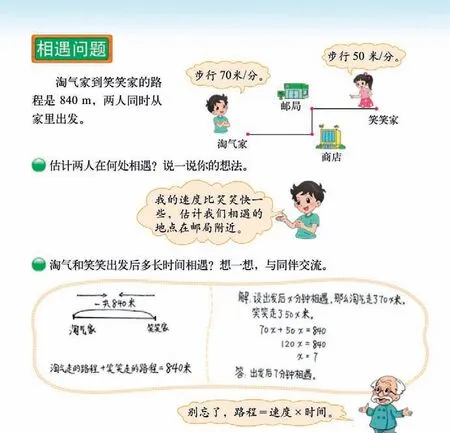
值得注意的是一般情况下，教材是鼓励学生利用多种方法解题，而这个内容教材却只给了一种解法。即使使用方程解决问题，同样也有“速度和×时间＝路程和”，为什么教材对“淘气路程+笑笑路程＝总路程”情有独钟呢？

我们不妨回到单元整体的角度来看待这个问题。本单元的主题是“用方程解决问题”，学生要经历将现实问题抽象为方程的过程，积累将现实问题数学化的经验，会用方程解决简单问题，进一步理解等量关系，感受方程的思想和价值。因此，从单元的角度看，《邮票张数》《相遇问题》既是本单元的学习内容，同时更是学习“用方程解决问题”的工具。

作者和学生们

用方程解决问题，学生应该学习什么呢？用方程解决实际问题的过程，一般有三个关键步骤：第一，依据题意找出数量之间的相等关系；第二，根据等量关系列出方程；第三，解方程。可见，利用方程解决问题的第一步，并不是直接向着问题的结果前进，而是先找到问题中的等量关系，并列出方程。本单元中的方程模型是“ax±bx=c”，教材中选取的《邮票张数》是“和倍问题”和《相遇问题》一样，都属于这一模型。这也回应了本单元的两个重点核心：一是建构ax±bx=c模型，二是学习一种代数解决问题的方法，先建立等量关系，列出方程，解方程进而解决问题，体现着模型思想。

有了对教材的整体把握，才能让我们更加明确每一节课的重点，在《相遇问题》这节课中，学习的目的不是简单地让学生会解相遇问题的题目，而是理解和构建ax±bx=c模型，学习一种新的解决问题的思路。通过先建构等量关系列方程，解方程即解决问题，进而更好地培养学生的代数思维。

在使用中发展代数思维

（一）适当增加一些利用代数方法解决问题的要求

利用字母表示等量关系，进而解决问题，是不同于学生惯有的用算术思维解决问题的新策略，是一种新的思维方式。学生的不习惯是正常现象。教师要引导学生从新的思维方式和新的解题策略的角度来认识用方程解决问题。同时，我们必须清楚地认识到，利用方程解决问题本身是代数思维培养的重要途径。从我们自身的认知中首先不排斥用方程解决简单问题，要有意识地鼓励学生尝试用方程解决问题，并不断激励学生。如在教学中，我们可以说“既然你已经会用算术的方法解决问题了，是否可以接受新的挑战呢？”让会用算术法解题的学生也能意识到，用方程解决问题是自己的一项新本领，进而愿意用新的思维方式去解决原来的问题。

（二）鼓励算法多样化中的代数方法

新的课程改革鼓励学生学习过程中的算法多样化，算法多样化可以丰富学生对问题本身的感知，各种方法之间建立联系，也是对学生高阶思维能力的培养。算法多样化的价值已经成为教师的基本共识。在教学中，可以鼓励学生在算法多样化中体现“数学思维”上的多样化，从解题方法的多样化，到解题策略上的多样化，最后到思维方式的多样化。例如下面的问题：

长方形的周长是24厘米，宽是3厘米，长方形的长是多少厘米？

学生经常出现下面几种不同的解题方法：

方法一：24÷2-3=9

方法二：（24-3×2）÷2=9

方法三：（3+5）×2=16

（3+6）×2=18

（3+7）×2=20

（3+8）×2=22

（3+9）×2=24

方法四：（3+x）×2=24

对比四种不同解题方法，我们不难发现，方法一和方法二属于解题思路的不同，方法一是先求出长宽之和减去宽等于长，方法二是用周长减去两个宽再除以2等于一个长。方法三与前两种方法的不同在于策略上的差异，是通过尝试列举获得结果。方法四则是用代数的方法解决问题。前三种方法虽然有思路上的不同、策略上的不同但还都是在算术思维的范畴内思考问题，而第四种方法则是从代数思维角度构建等量关系列出方程，通过解方程获得答案，是一种思维方式上的多样化。和学生共同分析各种方法之间的联系和差异，鼓励学生从不同的解题思路走向不同的解题策略，再走向思维方式的多样化，可以更好提高学生解决问题的能力，促进学生算术思维和代数思维的共同发展。

习惯的力量是强大的！代数思维作为与算术思维不同的一种思维方式，需要从小培养，让学生在两种思维的碰撞、交流、交汇中不断成长，期待代数思维能像算术思维一样，在学生头脑中变得自然、顺畅！