基于大数据技术的甘肃省农业综合实力动态变化分析

□魏 赟

（兰州城市学院电子与信息工程学院 甘肃 兰州 730070）

甘肃省土地面积约占全国总土地面积的4.7%，域内有黄河、长江、内陆河三大流域，处于黄土高原、内蒙古高原和青藏高原的交错地带，境内河谷纵横，山多川少，海拔除局部低于1 000 m 外，一般在1 000～3 000 m 之间，是山地型高原区，自然条件复杂，有山地、高原、丘陵、盆地、河谷、平原等多种地貌，各市（州）区域间差异性较大。降雨量从西向东逐步增加，西部降雨量最低在50 mm 以下，最高在陇南市和甘南藏族自治州部分，在600 mm 以上，有干旱、半干旱、半湿润、湿润四大类型地带。由于地区差异较大，发展理念不同，从而导致农业生产水平、农作物种植方式、农业生产资料投入量、农业生产产出、土地承载力、农民劳作方式等方面存在很大差异。

为了分析甘肃省各市（州）农业综合实力的动态变化以及对农村居民人均可支配收入带来的影响，利用动态聚类分析法、贝叶斯准则多类逐步判别分析方法对1995 年、2005 年、2015 年、2018 年甘肃省14 个市（州）农业综合生产力的动态变化进行分析。

1 方法与原理

1.1 动态聚类分析

动态聚类又称为逐步聚类方法，其聚类的步骤是，先按照一定的方法选取一批凝聚点，然后让其余样品向凝聚点凝聚，这样由点逐渐凝聚成类，得到初始的分类。但由于初始的分类不一定合理，必须进行修改，常用的办法是按照最近距离原则修改不合理的分类，直到分类趋于合理为止[1-3]。动态分类凝聚点的选择与分类方式如下。

（1）凝聚点的选择。凝聚点是一批被当成类中心的具有代表性的点。第一种方法是根据经验选择凝聚点，即依据专家经验，预先将样品分为若干类，并从每一类中选择一个具有代表性的样品作为凝聚点。第二种方法是只确定预分的类，然后通过计算得到每一类的重心，将这些重心作为凝聚点。第三种方法是用密度法选择凝聚点，即以某个整数d为半径，在m维空间中，落在以d为半径的球体内的样品数，称为以该样品为中心的空间中点的密度。当计算好所有样品点的密度后，首先选择密度最大的样品作为第一凝聚点，并且人为地确定一个整数D，然后选出第二大密度的点，如果该点与第一凝聚点的距离大于D，则作为第二凝聚点，否则该点就不能作为凝聚点，这样依次进行，直到全部样品选择完毕。第四种方法是用前K个样品作为凝聚点。本研究采用第二种方法进行动态聚类分析。

（2）初始分类。第一种方法是凭经验人为地将样品进行初步分类。第二种方法是选择凝聚点后每个样品按照与其最近距离的凝聚点进行归类。第三种方法是选择一批凝聚点后每个凝聚点自成一类，将样品依次归入其距离最近的凝聚点的第一类，并立即重新计算该类的重心，以代替原来的凝聚点，再计算下一个样品的凝聚点，直到所有样品都归类为止。第四种初始分类方法先将样品的原始数据进行标准化处理，用Xij表示已标准化处理后的第i个样品第j个指标。采用第四种初始分类方法进行处理。

欲将全部样本分为K类，对于每一个样本计算见下式。

如果与这个数接近的整数为k，则将样本xi归入第k类。

（3）分类函数。动态聚类的方法很多，有按批修改法、逐个修改法和等混合法。动态聚类的不同方法主要是以修改分类的不同原则来区分。下面主要讨论按批修改方法。在按批修改法中，每一步修改都将使对应的分类函数缩小，并且分类函数最终趋于定值，即计算过程是收敛的。

假定x1、x2、…、xn表示n个样品点，初始分类为K类，即G1、G2、…、Gk，重心记为，每类样品数记为n1、n2、…、nk。

定义Xi与类GJ的距离，见下式。

定义分函数，见下式。

式中：L(i)表示xi所属类的标号。

按批修改的原理就是，使式（6）的分类函数逐渐减小，直至不能再减小为止。该式所定义的分类函数，实质上是系统聚类中的离差平方和。

1.2 贝叶斯准则多类逐步判别分析

根据动态聚类分析法，得出对某类样品的分类结果，但分类的结果是否完全合理，需要利用其他方法进行验证分析，利用贝叶斯准则多类逐步判别分析方法，对动态聚类分析结果进行判别分类。具体计算过程：根据威尔克斯统计量挑选对分类影响最大的变量，在贝叶斯准则下建立判别函数，进行多类判别，从而确定样品的最可能归类。

对于一个具有p个指标的样品，要判断其归类于m个组中的哪一组。判别分析的任务是把p维空间按照某种准则划分为互不相交的g个区域R1、R2、R3、…、Rg，并把待判样品X看成是p维空间的一个点，通过计算该样品属于m个组的条件概率大小，经比较后将这个样品归入概率最大的一组内。

分析计算中对于给定的总体先验概率，平均损失为最小的划分空间规则称为贝叶斯准则，划分结果的Ri称为关于总体先验概率的贝叶斯解。

对于第i个总体的第t个子样，一般采用下面的计算公式得到总体参数均值向量和协方差矩阵，具体见下式。

对于所建立的判别函数的检验，可采用维尔克斯统计量∧。

式中：W为组内方差协方差矩阵，B为组间方差协方差矩阵，X为总体的均值向量，计算公式如下。

为了实现逐步计算，同样利用矩阵变化法，对于T、W作如下变化，以W为例，见下式。

式中：r为待处理变量号，l为变换的步数。

如果在第l步时已入选L个变量，现在要检验第r个变量是否应入选，应计算下列F统计量，见下式。

如果F≤F2，则认为该判别能力不显著，应予以剔除，F2亦事先规定。在规定了F1和F2以后，利用上述方法一直继续到既无已选变量可舍去，又无未选变量可入选为止。利用入选的一组判别变量，可按照贝叶斯准则建立判别函数。

在实际计算分析时，分以下两个过程进行。先进行动态聚类分析，在此基础上，将已分类的结果作为贝叶斯准则多类逐步判别分析的预分类，再进行判别分析。分析时所用的数据从1995 年开始，到2018 年结束，均采用《甘肃年鉴》《甘肃发展年鉴》中的数据。农业综合实力由甘肃省14 个市（州）的农业人口（万人）、耕地面积（hm2）、农作物播种面积（千hm2）、粮食总产量（万t）、当年出栏牛猪羊总数（万头只）、农林牧渔总产值（万元）、农业总产值（万元）、农村居民人均可支配收入（元）、社会消费品零售总额（万元）、农林牧渔从业人员（万人）、农业机械总动力（万kW）、农村用电量（万kW·h）、化肥施用折纯量（t）等13 个指标构成。

2 结果分析

2.1 1995 年甘肃省14 个市（州）农业综合实力动态聚类分析

甘肃省14 个市（州）的农业综合实力的动态聚类分析采用第二种方法，预先分为4 类，即农业综合实力分为强、较强、较弱、弱[4]。利用甘肃省1995 年《甘肃年鉴》《甘肃发展年鉴》中的农业生产数据，由式（1）～式（6），对甘肃省14 个市（州）的农业综合实力进行动态聚类分析，所得结果见表1。

根据表1 的分类结果，酒泉市、张掖市、威武市为第4 类，农业综合实力为强；天水市、定西市、陇南市、平凉市、庆阳市为第3 类，农业综合实力为较强；兰州市、白银市、临夏回族自治州为第2 类，农业综合实力为较弱；嘉峪关市、金昌市、甘南藏族自治州为第1类，农业综合实力为弱。

表1 1995 年甘肃省14 个市（州）农业综合实力动态聚类分析结果

为了验证上述分类结果的正确性，将动态聚类分析的分类结果作为贝叶斯准则多类逐步判别分析的预分类进行判别分析，分析所用的原始数据和动态聚类分析的数据完全一样。由式（7）～式（16），对甘肃省14 个市（州）的农业综合实力进行贝叶斯准则逐步判别分析，所得结果见表2、表3、表4。在贝叶斯准则逐步判别分析的计算过程中，挑选变量和剔除变量所用的F1、F2值均为1。2005 年、2015 年、2018 年的F1、F2值完全相同。

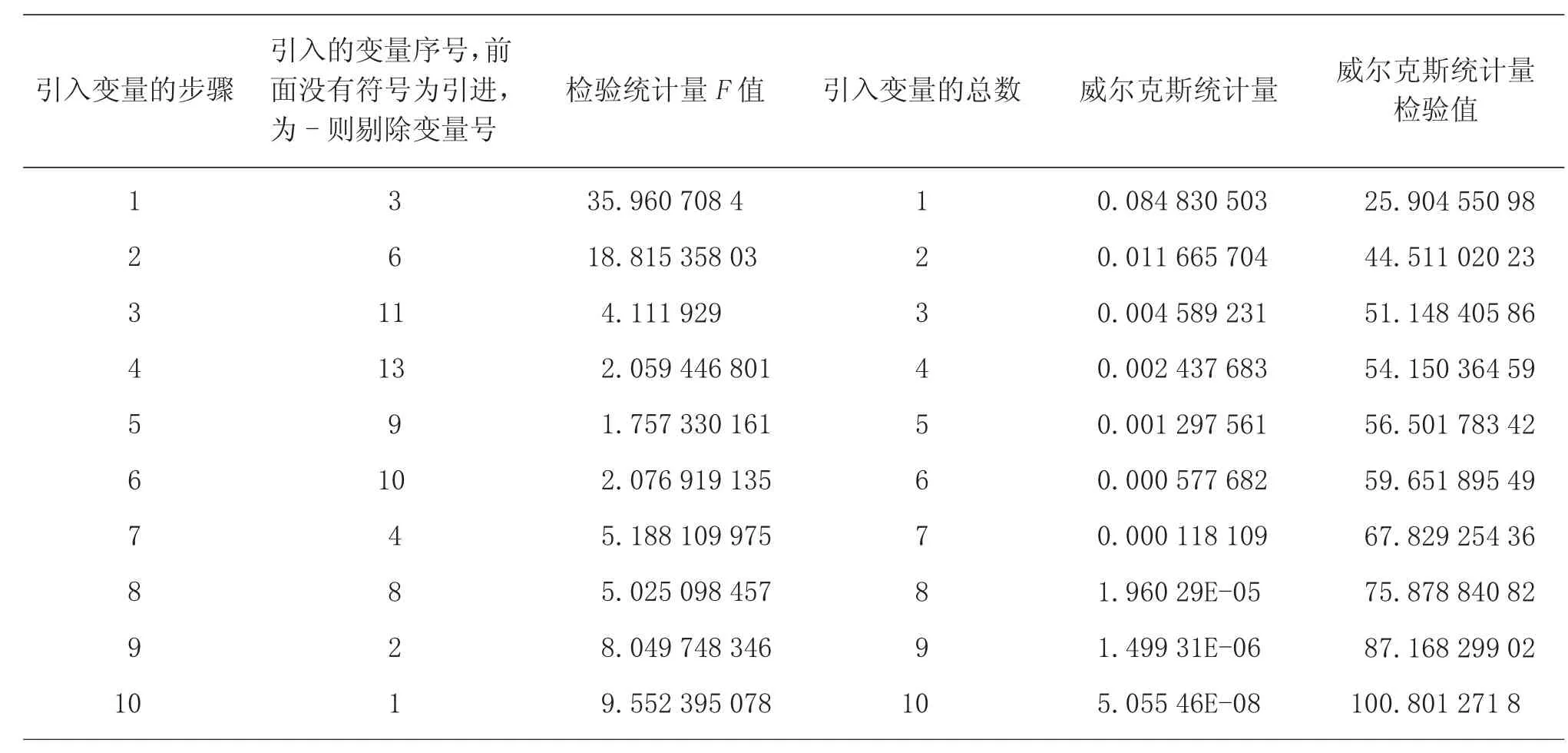
表2 贝叶斯准则逐步判别分析挑选变量的结果（1995 年）

表3 判别系数（未选入变量系数为0，1995 年）

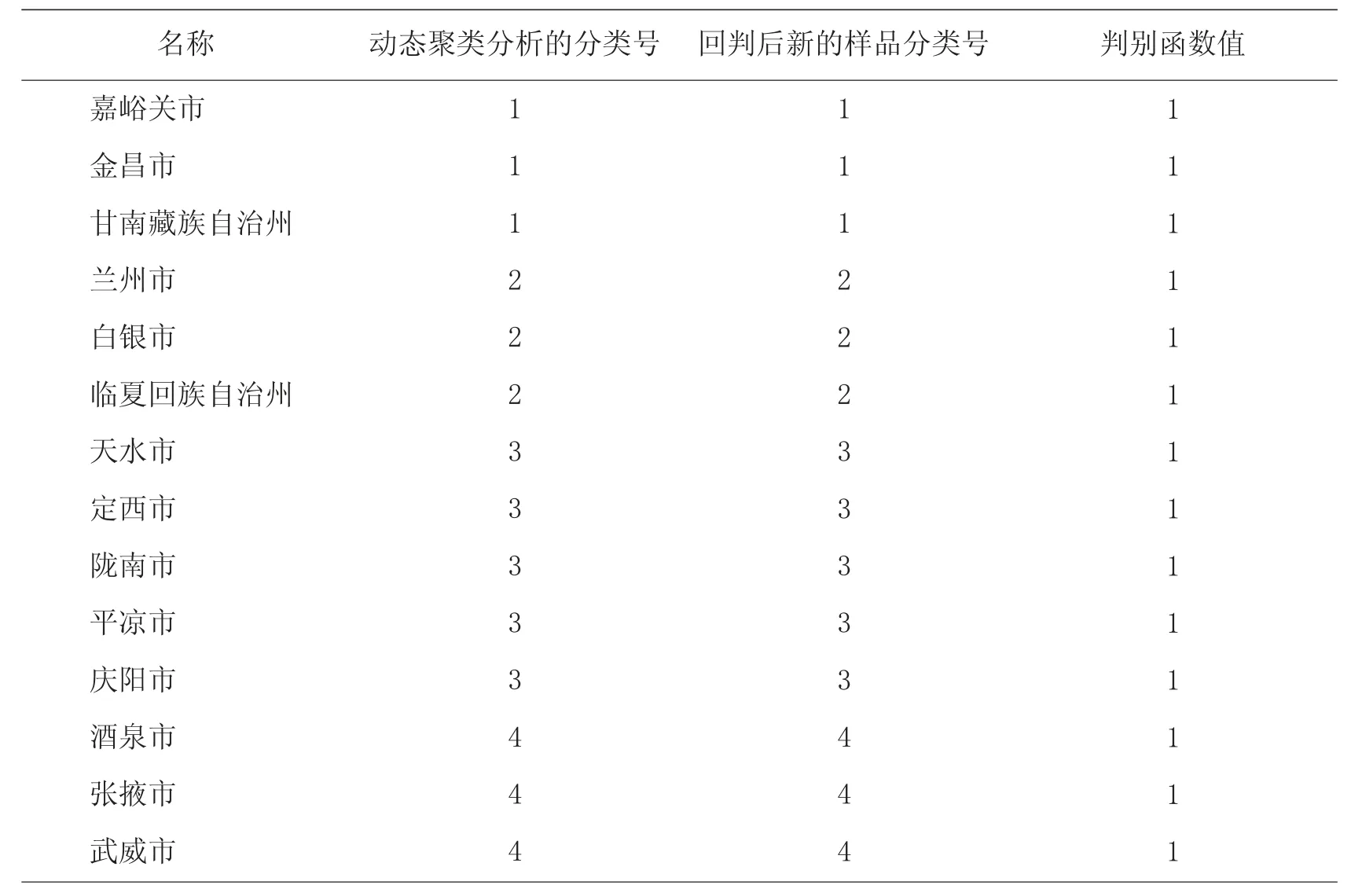
表4 贝叶斯准则逐步判别分析结果（1995 年）

1995 年对甘肃省14 个市（州）的农业综合实力进行贝叶斯准则逐步判别分析时，按照弱、较弱、较强、强4 种类型进行分类，与之对应的有4 类判别函数。在表3 中，第1 类、第2 类、第3 类、第4 类这4 列的14 个判别系数，分别构成农业综合实力为弱、较弱、较强、强4 种类型的判别函数，其中对应当年出栏牛猪羊总数、农业总产值、农村用电量这3 个指标的判别系数为0。

由于威尔克斯统计量的分布函数相当复杂，一般采用巴特莱特近似式将其与χ2分布联系起来。威尔克斯统计量和χ2的计算结果见表2 的第5 列、第6列。表2 引入变量的自由度为10×（4-1）=30，近似服从于分布χ2（30）。查表得χ20.001（30）=59.703，计算出威尔克斯统计量的检验值χ2=100.801 271 8＞χ20.001（30），说明表2 引入的10 个变量构成的判别函数达到极显著水平，完全能够对甘肃省14 个市（州）农业综合实力进行判别分析。

在表4 中，第3 列“回判后新的样品分类号”的数据是贝叶斯准则逐步判别分析的结果，可见利用动态聚类分析所得结果与贝叶斯准则多类逐步判别分析的结果完全一样。由此说明，1995 年甘肃省14 个市（州）农业综合实力的分类结果准确。

2.2 2005 年甘肃省14 个市（州）农业综合实力聚类分析

动态聚类分析、贝叶斯准则逐步判别分析所采用的原始数据为2005 年甘肃省14 个市（州）的农业生产数据，分析方法与前面相同，计算结果分别见表5、表6、表7、表8。

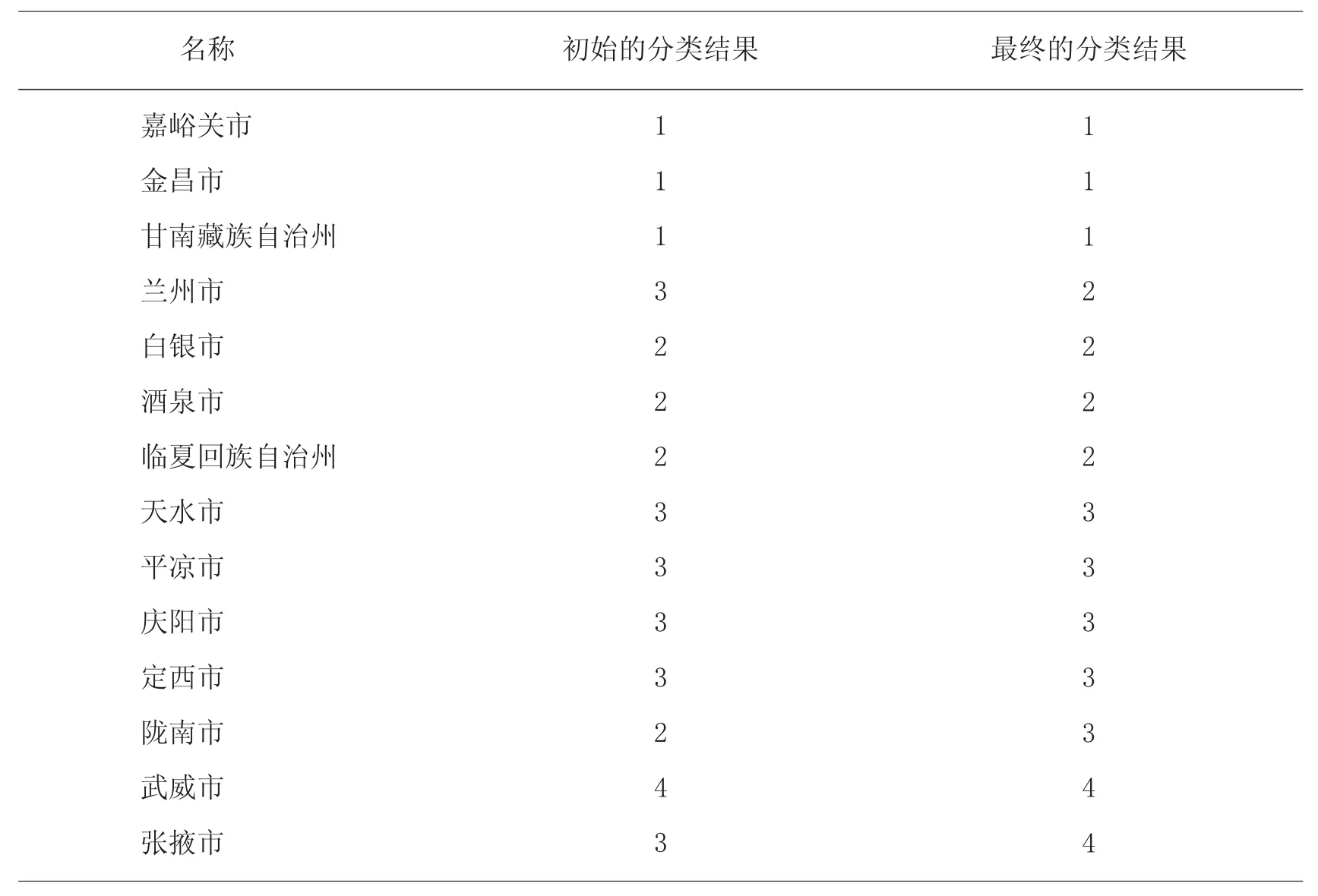
表5 2005 年甘肃省14 个市（州）农业综合实力动态聚类分类结果

表6 贝叶斯准则逐步判别分析挑选变量的结果（2005 年）

表7 判别系数（未选入变量系数为0，2005 年）

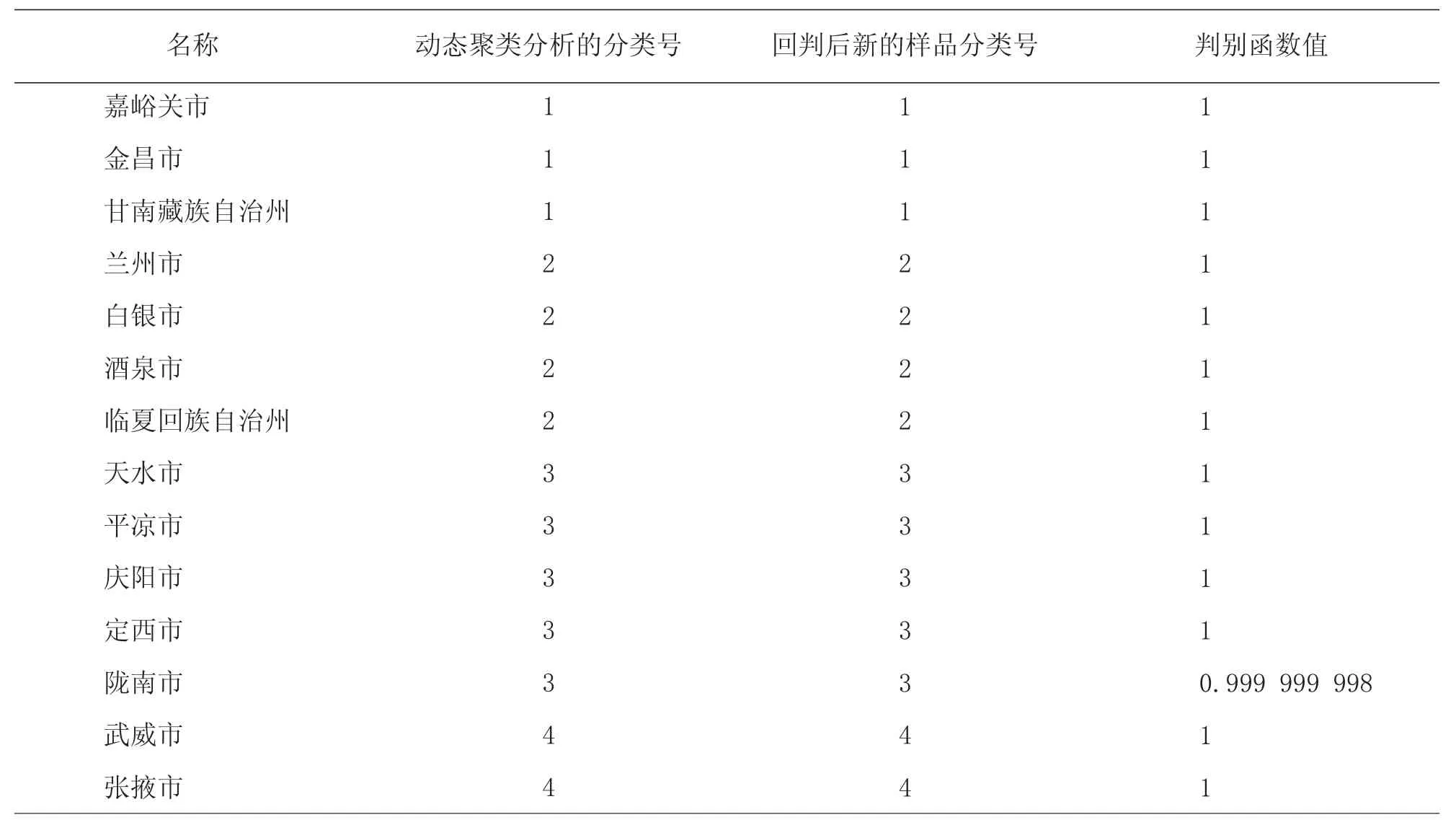
表8 贝叶斯准则多类逐步判别分析结果（2005 年）

根据表5 的最终分类结果可知，张掖市、威武市为第4 类，农业综合实力为强；天水市、平凉市、庆阳市、定西市、陇南市为第3 类，农业综合实力为较强；兰州市、白银市、酒泉市、临夏回族自治州为第2 类，农业综合实力为较弱。与表1 相比，酒泉市的分类由第4 类变为第2 类，农业综合实力由强下降为较弱；嘉峪关市、金昌市、甘南藏族自治州为第1 类，农业综合实力为弱。

表6 中引入变量的自由度为5×（4-1）=15，近似服从于分布χ2（15）。查表得χ20.001（15）=37.697，计算出威尔克斯统计量的检验值χ2=58.950 695 99＞χ20.001（15），说明表6 中引入的5 个变量构成的判别函数达到极显著水平，对甘肃省14 个市（州）农业综合实力进行判别分析，结果可信度高。

2005 年对甘肃省14 个市（州）的农业综合实力进行贝叶斯准则逐步判别分析时，分类方法同前。在表7 中，第1 类、第2 类、第3 类、第4 类这4 列的14 个判别系数分别构成4 类判别函数。其中，对应耕地面积、当年出栏牛猪羊总数、农林牧渔总产值、农村居民人均可支配收入、社会消费品零售总额、农林牧渔从业人员、农村用电量、化肥施用折纯量8 个指标的判别系数为0。

根据甘肃省14 个市（州）2005 年农业生产数据，利用贝叶斯准则多类逐步判别分析进行判别分类，与动态聚类分析的结果一致。因此，2005 年甘肃省14 个市（州）农业综合实力的分类结果同样是可信的。

2.3 2015 年甘肃省14 个市（州）农业综合实力聚类分析

动态聚类分析、贝叶斯准则逐步判别分析计算时所用的原始数据为2015 年甘肃省14 个市（州）的农业生产数据，计算方法同前，具体的结果见表9、表10、表11、表12。

表9 2015 年甘肃省14 个市（州）农业综合实力动态聚类分析结果

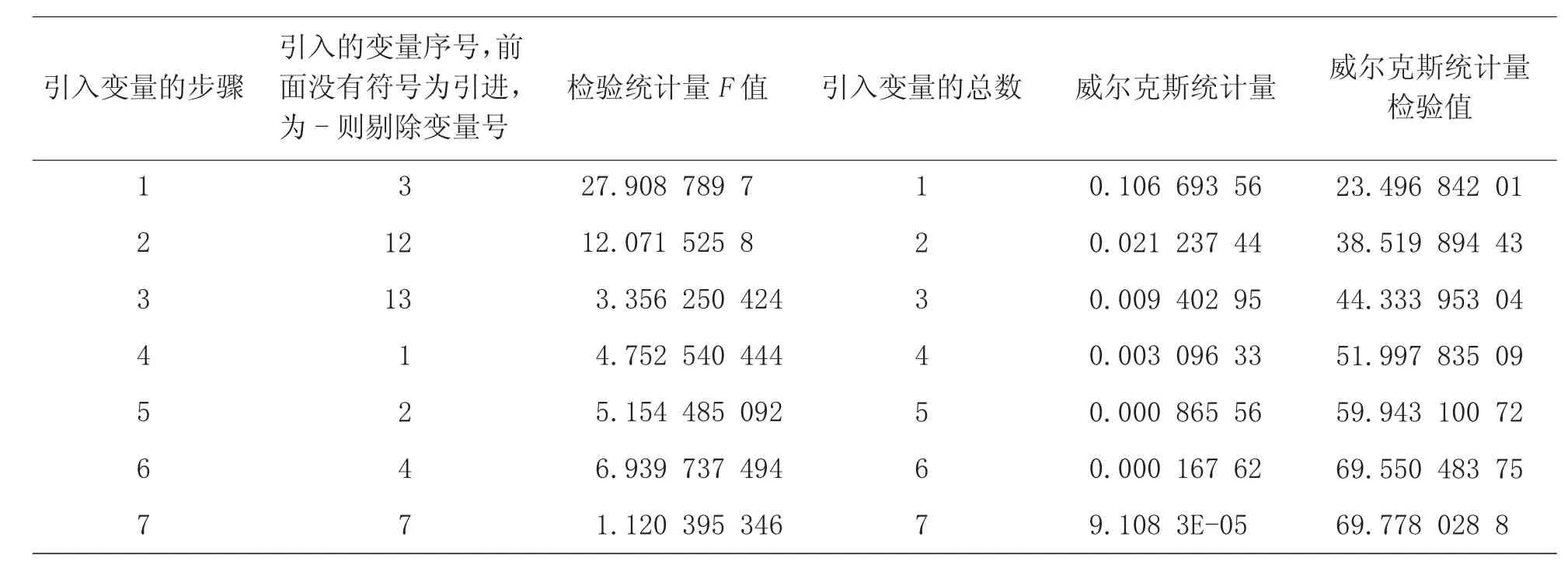
表10 逐步挑选变量过程结果（2015 年）

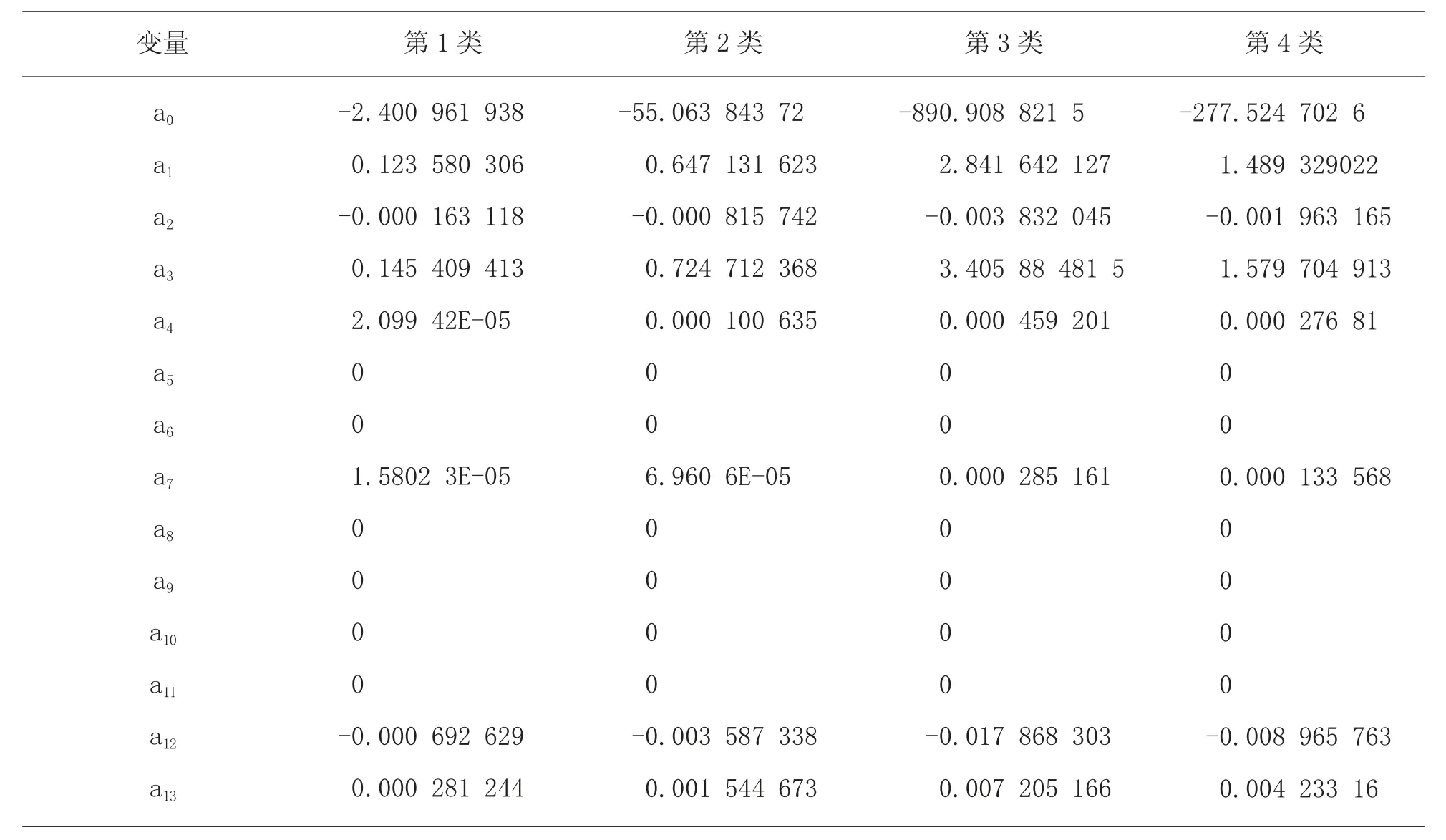
表11 判别系数（未入选变量系数为0，2015 年）

根据表9 的最终分类结果，与表5 的分类结果相同，说明从2005—2105 年，甘肃省14 个市（州）的农业综合实力没有出现变动。

表10 中引入变量的自由度为7×（4-1）=21，近似服从于分布χ2（21）。查表得χ20.001（21）=46.797，计算出威尔克斯统计量的检验值χ2=69.778 028 8＞χ20.001（21），说明表10 引入的7 个变量构成的判别函数达到极显著水平，对甘肃省14 个市（州）农业综合实力进行判别分析，所得结果可信度高。

2015 年对甘肃省14 个市（州）的农业综合实力进行贝叶斯准则逐步判别分析时，分类方法同前。在表11 中，由判别系数构成的4 类判别函数中，对应当年出栏牛猪羊总数、农林牧渔总产值、农村居民人均可支配收入、社会消费品零售总额、农林牧渔从业人员、农业机械总动力6 个指标的判别系数为0。

据表12 可知，动态聚类分析、贝叶斯准则多类逐步判别分析的分类结果完全相同。说明用动态聚类分析、贝叶斯准则多类逐步判别分类后，2015 年甘肃省14 个市（州）的农业综合实力所得结果的可信度高。

表12 贝叶斯准则多类逐步判别分析结果（2015 年）

2.4 2018 年甘肃省14 个市（州）农业综合实力聚类分析

根据2018 年甘肃省14 个市（州）农业生产数据，利用动态聚类分析、贝叶斯准则逐步判别分析法，对2018 年甘肃省14 个市（州）的农业综合实力进行分类，结果见表13、表14、表15、表16。

表13 2018 年甘肃省14 个市（州）农业综合实力动态聚类分析结果

表14 贝叶斯准则多类逐步判别分析挑选变量的结果（2018 年）

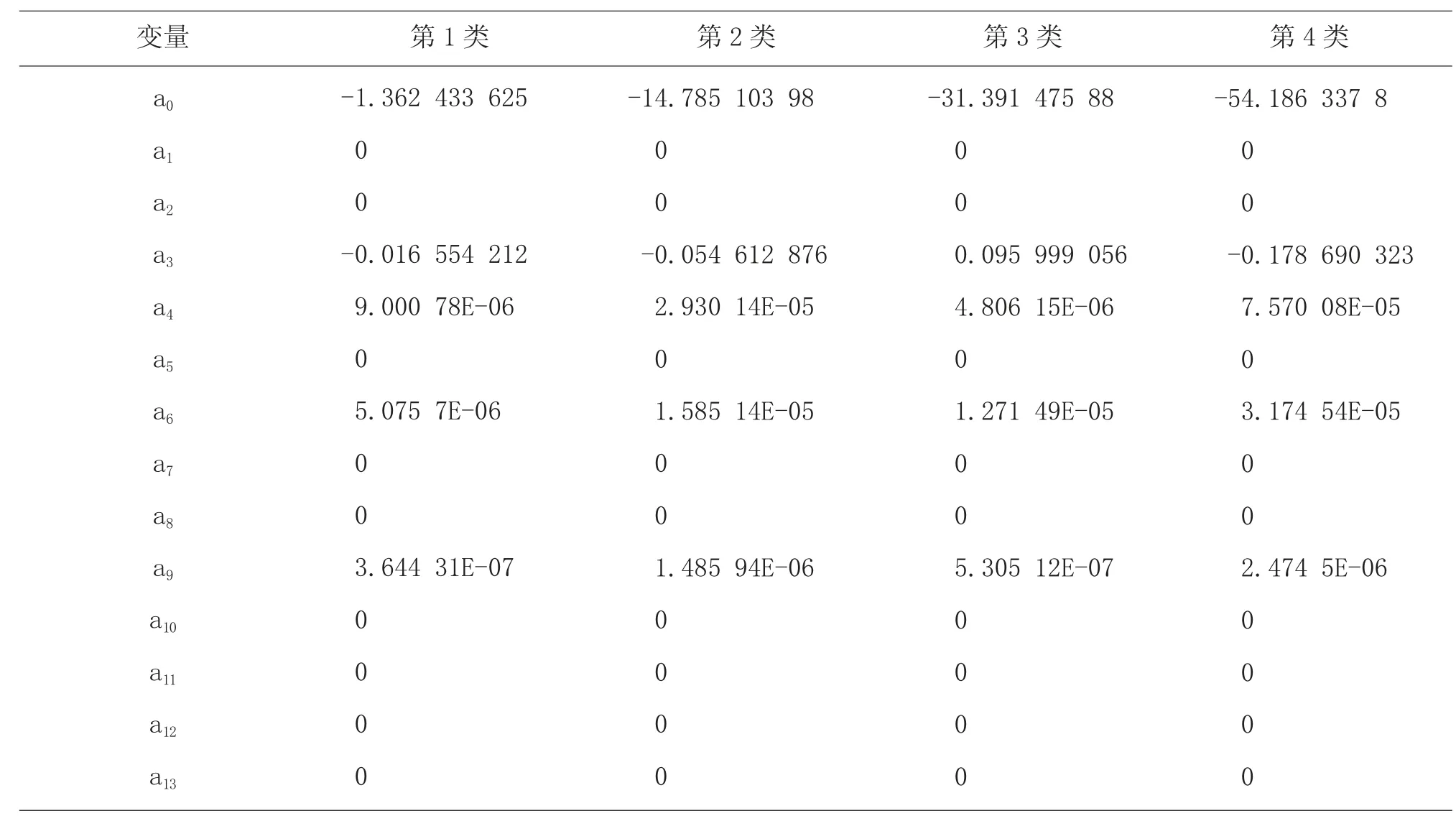
表15 判别系数（未入选变量系数为0，2018 年）

由表13 动态分类的分析结果可知，到2018 年，白银市的动态聚类由2 变为3，说明白银市的农业综合实力由较弱提升为较强，其余市（州）的农业综合实力与2015 年相同，没有出现变化。

表14 中引入变量的自由度为4×（4-1）=12，近似服从于分布χ2（12）。查表得χ20.001=32.909，计算出威尔克斯统计量的检验值χ2=45.130 499 73＞χ20.001（12），说明表14 引入的4 个变量构成的判别函数达到极显著水平，利用判别函数对甘肃省市（州）农业综合实力进行判别分析，所得结果可信度高。

2018 年对甘肃省14 个市（州）的农业综合实力进行贝叶斯准则逐步判别分析时所用分类方法同前。4 类判别函数中对应市（州）的农业人口、耕地面积、当年出栏牛猪羊总数、农业总产值、农村居民人均可支配收入、农林牧渔从业人员、农业机械总动力、农村用电量、化肥施用折纯量9 个指标的判别系数为0。

根据表16 贝叶斯准则多类逐步判别分析的结果可以看出，在2018 年，利用动态聚类分析、贝叶斯准则多类逐步判别分析，对甘肃省14 个市（州）的农业综合实力进行聚类分析和判别分析，结果完全一致，因此，2018 年甘肃省14 个市（州）农业综合实力的类型划分很准确。

表16 贝叶斯准则多类逐步判别分析结果（2018 年）

3 结束语

利用动态聚类分析、贝叶斯准则多类逐步判别分析，对甘肃省14 个市（州）1995—2018 年的农业综合实力分别进行了4 次聚类分析和判别分析，结果完全一致，说明对甘肃省14 个市（州）的农业综合实力划分类别是可信的。经过24 年的发展变化，14 个市（州）的农业综合实力属于强类别的是武威市、张掖市。白银市的农业综合实力，截至2018 年，分类号由2 变为3，农业综合实力也由较弱提升为较强。到2018 年农业综合实力属于较强类别的是白银市、天水市、平凉市、庆阳市、定西市、陇南市。酒泉市的农业综合实力起初为第4 类，属于农业综合实力强的一类，但到2005 年下降为第2 类，属于农业综合实力较弱的一类。农业综合实力属于较弱类别的是兰州市、酒泉市、临夏回族自治州。嘉峪关市、金昌市、甘南藏族自治州3 个市（州）农业综合实力在1995—2018 年间未发生变化，一直属于弱类别。中国是农业大国，农业综合实力提升对当代中国发展具有重要意义。通过相关数据分析可以看出，甘肃省14 个市（州）中，有的市（州）农业综合实力由弱变强，有的市（州）农业综合实力由强变弱，这与当地政府的农业发展策略、资源水平等因素有关，如何从中汲取具有价值及意义的策略，正是研究者亟待研究与解决的问题。