具有工程适用性的复合材料机翼结构快速设计

艾 森，常 亮，罗利龙，王立凯

(中国飞机强度研究所 计算结构技术与仿真中心，陕西 西安 710065)

1 引 言

由于复合材料具有比强度和比模量高、良好的可设计性、成型工艺好、耐腐蚀、耐热性好等优点，使其在无人机结构中所占的比例越来越大，如美国的全球鹰无人机、X-45无人战斗机等，复合材料的用量占比达到总重量的65%，甚至是90%以上[1,2]。在无人机结构设计中，一般通过选择复合材料层合板的厚度、角度及铺层顺序，来获得理想的方向刚度，并提供最佳的设计方案。但在实际应用中，复合材料的选材设计面临着诸多问题和挑战。比如，对于复合材料层合板的参数，除常规的几何尺寸外，还包括铺层比例、铺层角度、铺层顺序[3]，这些参数的设计将使得整个设计空间表现为组合爆炸的现象，尤其针对铺层顺序问题，更是给问题的求解带来难以预估的计算代价。

为了解决复合材料层合板设计过程中的组合爆炸问题，很多学者都采用基于演化类的智能优化算法，来获得满足性能指标的优化结果。例如，Shrivastava等利用经典的遗传算法对一个运输飞机复合材料机翼盒段进行了设计，达到减重29%的效果[4]。Bach等采用序列基因算法(permutation GA)实现了机翼结构的优化[5]。Dutra等引入多个准则，并结合数据库，对复合材料平板结构进行了优化选材[6]。郑国文等基于改进双种群遗传算法对复合材料层合板的铺层顺序进行了优化，优化效率显著提升[7]。林壮壮综合考虑了复合材料的设计原则及制造工艺，并基于多岛遗传算法，对复合材料层合板的厚度和角度开展了优化设计，减重效果明显[2]。

虽然智能优化算法可在复合材料设计空间内找到全局最优解，但由于算法基于群体进化的寻优机制，需要反复地进行结构分析，计算量大、效率低[3]，一般不适用于大型复杂结构或基于超精细有限元模型的结构优化设计。

针对大型复合材料结构，尤其是基于精细有限元模型的结构设计问题，工程设计人员一般采用成熟的商业软件来获得复合材料铺层厚度以及铺层顺序。如，陈彦达等基于OptiStruct软件对大型机翼翼盒结构进行了优化设计，实现减重20%[8]。李宇峰等基于Hypersizer软件开展了复合材料舱门结构优化设计，降低了结构重量[9]。卢秉贺等利用Hypersizer软件，对复合材料结构进行了铺层设计和过渡区的设计，获得了满足工程要求的设计结果[10]。

这些成熟的商业软件往往价格昂贵，且技术受制于人，核心技术更是难以获取。为了提高复合材料结构的设计效率，实现自主设计软件的崛起，本文针对复合材料机翼结构，开展了具有工程适用性的复合材料结构快速设计技术研究。首先，在复合材料铺层厚度设计中，采用满应力/应变方法，实现大规模变量的快速厚度优化；然后，基于厚度优化结果，研究工程化的厚度圆整方法；最后，借助自主研发的工程材料数据库，实现铺层顺序的快速设计，从而为大型复合材料结构的设计提供快速、高效的工程化方法。

2 复合材料结构快速设计方法

2.1 设计方法总体概述

复合材料结构的铺层厚度、铺层角度以及铺层顺序具有良好的可设计性，这些设计变量一般为离散变量。在进行具体设计时，通常将离散变量转化为连续变量，就可以采用成熟的连续变量优化方法进行寻优，比如准则法或数学规划法。连续变量优化后的铺层厚度一般不是单层厚度的整倍数，需要进一步圆整，以满足工艺要求。此外，考虑到工程中常用的铺层角度为0°、±45°以及90°，只有在考虑某些特殊因素时(气动剪裁设计)，才会使用其他角度。因此，本文不涉及铺层角度的设计。

复合材料结构铺层厚度、铺层顺序设计过程如图1所示。具有工程适用性的复合材料结构铺层厚度、铺层顺序设计过程可描述为：对建立的有限元模型划分设计区域，建立设计变量与属性区的对应关系，构建各属性区的约束条件以及设计目标。通过此优化模型，利用满应变方法进行设计。由于满应力设计出的铺层厚度一般不是单层厚度的整倍数，这就需要对铺层厚度的设计结果进行圆整。在圆整后，利用工程材料数据库中的铺层顺序进行筛选，实现铺层顺序的设计。

图1 复合材料结构铺层厚度、铺层顺序设计过程

2.2 铺层厚度设计

对于铺层厚度而言，其直接与结构的重量相关。在优化过程中，通常不改变各个分层的顺序，而是只通过优化获得最佳的分层比例。目前，对于复合材料的优化，主要通过工程上常用的满应力方法进行。满应力方法收敛速度快、迭代次数少且与结构大小及结构复杂程度无关，特别适用于大型结构优化。

在复合材料设计中，当复合材料层压板受横向载荷作用时，应力分布比较复杂。层压板的铺层应力在各分层内是线性变化的，但从整个层压板来看，应力不是线性变化的，而是分段线性变化的。层压板的应变比较简单，应变是层压板厚度的线性函数。在层压板的最外层，应变最大，如图2所示。因此，在复合材料优化设计中，更适合用满应变的设计思想进行优化。

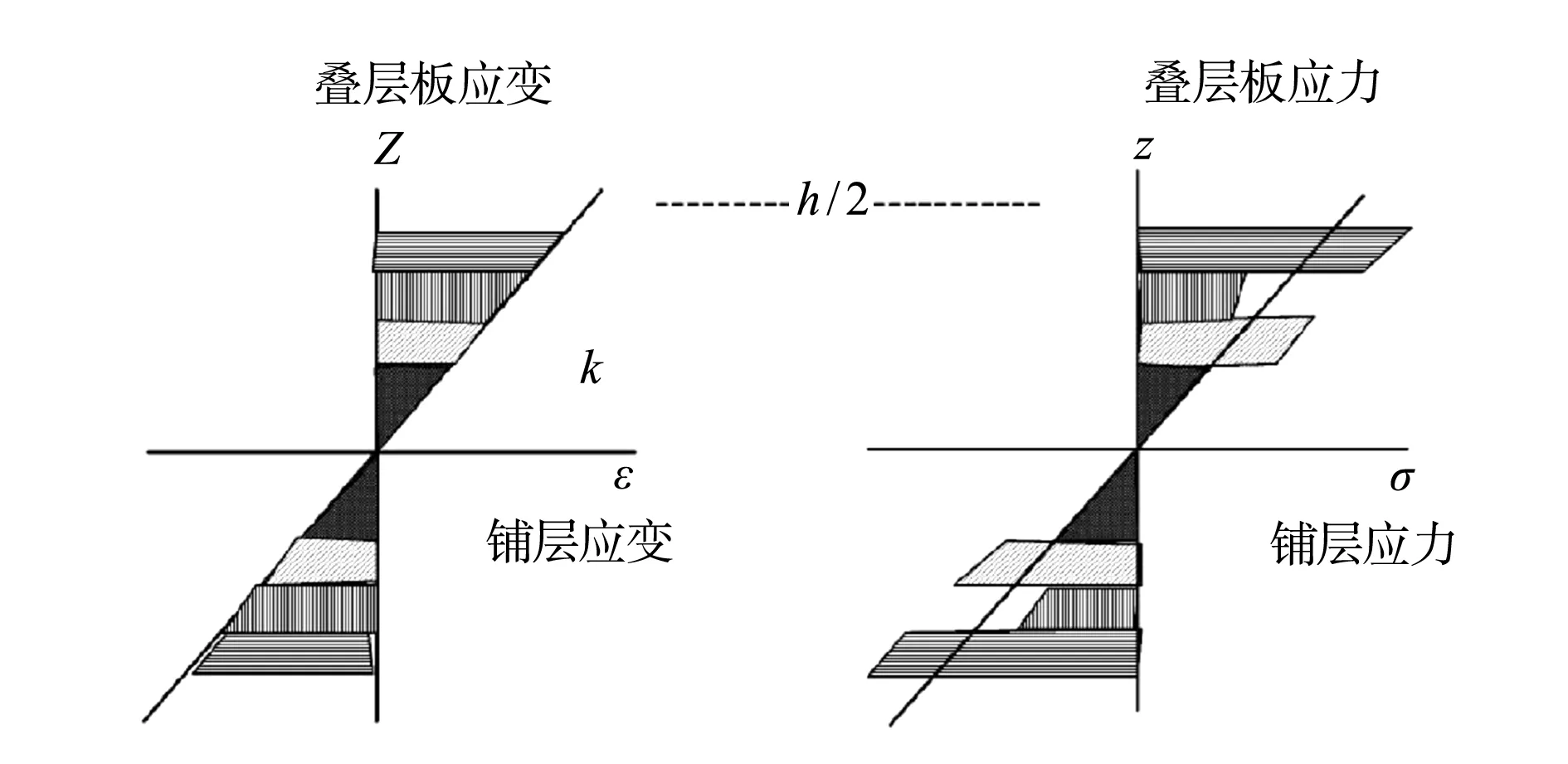
图2 层压板的应力应变示意图

满应变的核心在于应变比的计算，综合考虑复合材料层合板的拉、压、剪受力状态，应变比采用下述公式计算：

(1)

利用满应变准则，迭代过程采用下述公式：

(2)

以上各式中，εi max，εi min，γi max为许用应变(拉、压、剪)；εi工作为工作应变；Ti为设计变量(复合材料板的总厚度)；ξi为应变比；β为松弛系数。

2.3 厚度圆整方法

在完成满应变设计后，获得各分层的厚度，此时的厚度并不是单层厚度的整倍数，需要进行圆整。不同圆整策略得到不同的设计结果，本文采取的方式为相对差商法。具体实现过程为：

(1)读取优化结果；

(2)计算目标函数灵敏度系数：

(3)

(3)对总厚度进行圆整，然后在此基础上对±45°铺层进行圆整，0°和90°按照原始比例进行分配；

(4)枚举出满足离散取值要求的点，求出约束及目标函数偏差：

(4)

(5)找出偏差大于等于0的点，按其偏差值大小由小到大检验，第一个满足约束条件要求的即为圆整后的点。

2.4 铺层顺序设计

在复合材料铺层设计中，通常将各类设计约束及工艺约束纳入考虑范围，如对称均衡、相同角度的单向带层数不超过4层等。但在实际应用中，如果要全面考虑复合材料铺层的设计要求以及工艺约束，则只能通过利用铺层优化后的相关结果进行手工调整。

为了化简铺层设计的工作量，本文利用自主研发的工程材料数据库进行铺层顺序的设计。图3所示为工程材料数据库的前置界面，该数据库收录了国内航空常用复合材料力学性能数据和工程中常用的铺层顺序[11]。如对于具有10层的层合板，提供了[45/90/-45/0/0]s、[0/45/-45/0/0]s、[45/0/0/0/-45]s等41种铺层顺序，这些铺层顺序大多数在工程中得到了应用，并且满足设计、工艺等约束，用户可根据层合板的分层比例，在这些铺层顺序中筛选。

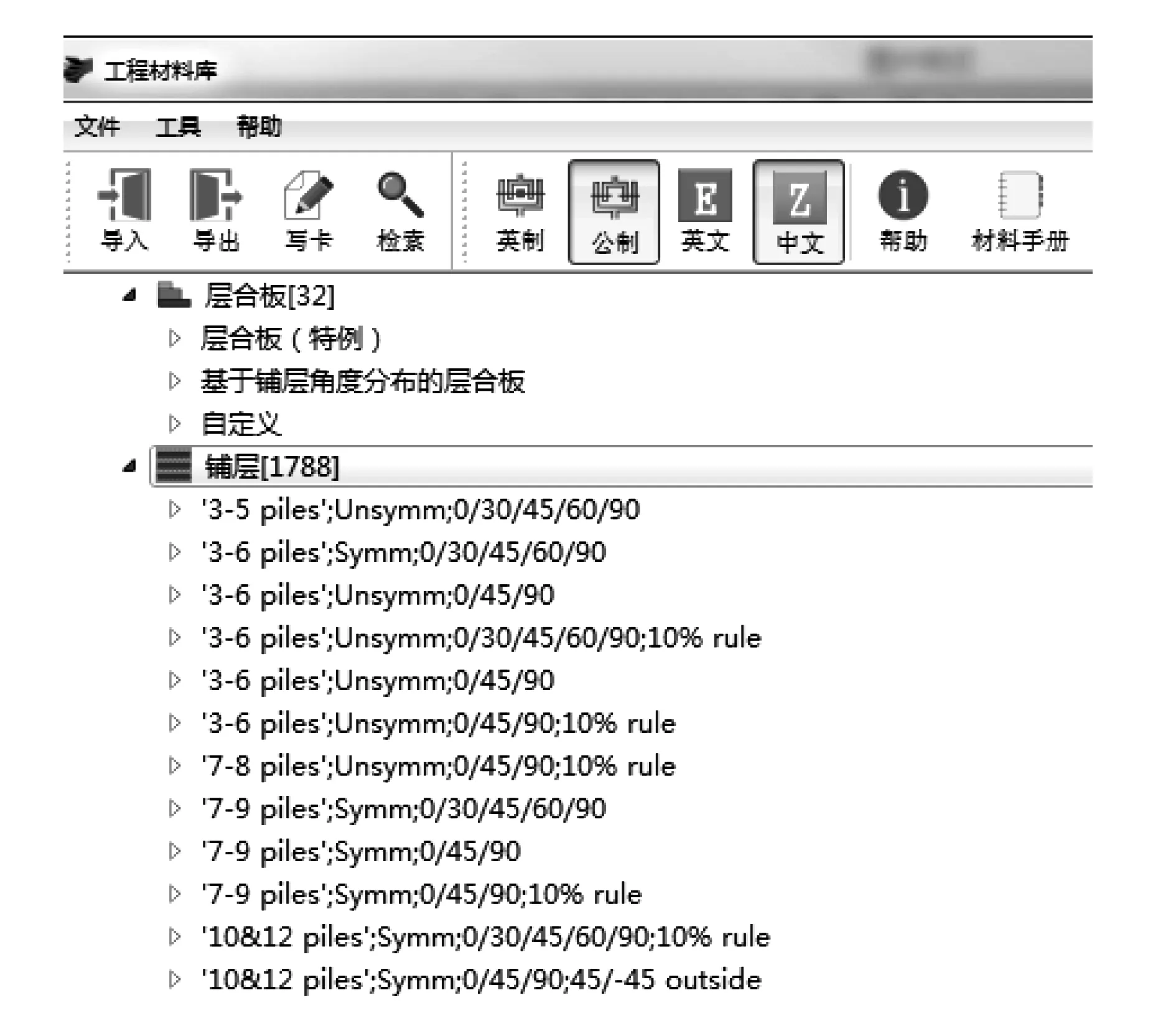
图3 工程材料数据库的前置界面

3 复合材料机翼结构铺层设计

针对某无人机机翼进行复合材料层合板的优化设计，如图4所示。机翼由内翼和外翼组成，在采用满应变设计时，每个设计区域由较多个单元组成，同一个区域作为一个设计区域，如图4中的A、B属性区。

图4 某无人机机翼有限元模型

采用满应变设计时，各层合板的分层厚度作为设计变量，并以设计区域的结构重量最小为目标，以复合材料的拉、压、剪强度值作为约束条件。满应变设计迭代曲线如图5所示，初始的结构重量为134.4kg，在经过10步迭代后，重量水平基本收敛，优化后的重量125.4kg，减重6.7%。优化前最大位移为637mm，优化后减小为628mm。

图5 满应变设计迭代曲线

如前所述，满应力优化的设计变量为各层合板的分层厚度，优化出的厚度并不是单层厚度的整倍数。以图4所示的A属性区为例进行说明。在A属性区，优化前后的总厚度、分层厚度以及圆整情况详见表1。复合材料单向带的厚度为0.125mm，优化后，A属性区的总厚度为单层的整数倍，但各分层厚度并不是单层厚度的整数倍。采用上节提到的圆整方法之后，A属性区的各个分层厚度得到了圆整。

表1 A属性区优化前后总厚度和分层厚度

圆整之后，需要针对各个分区的铺层顺序进行设计。工程材料铺层库中给出了常见层合板的铺层顺序，如果没有找到相应的层数，可以采用层数相加的方法进行叠加铺层。在A属性区，优化后的总层数为22层，分层比例为：0°层，41%；±45°层，50%；90°层，9%。在铺层数据库中并没有直接提供22层的铺层顺序，可以利用11层的铺层顺序叠加。如图6所示，铺层数据库提供了48种11层的铺层顺序方案，根据分层比例控制，可以筛选出22层的最终铺层为[45/0/0/0/-45/0/45/0/-45/0/90]s。

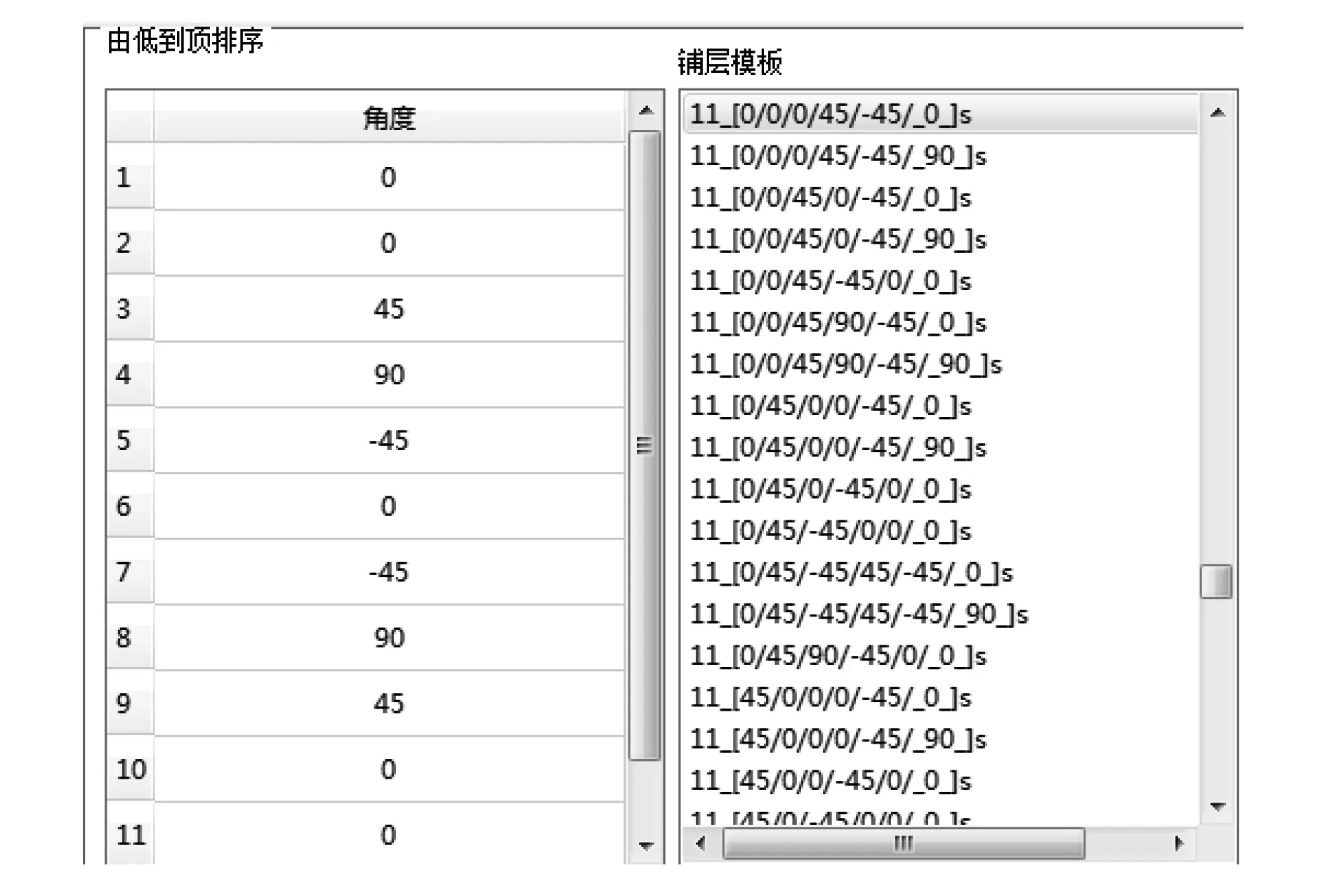
图6 层数为11层的铺层顺序

利用这种方法，完成所有属性区的铺层顺序设计，如图7所示。通过上述设计后，最大位移为613mm，比原始设计减小3.3%。基于铺层数据库可以快速实现各个铺层的顺序设计，最大化减小设计工作量。

图7 铺层设计后的位移云图

4 结 论

(1)为提供高效的复合材料铺层厚度、铺层顺序优化策略，分别基于满应变设计、相对差商法厚度圆整、工程材料数据库等方法，开展了面向工程的复合材料层合板快速设计技术研究，打通了全流程的快速设计通道。

(2)以某无人机复合材料机翼结构为验证对象，通过对各分区铺层厚度、顺序的设计，实现减重6.7%，最大变形下降了3.3%的设计效果，验证了本文提出的优化设计流程的可行性。

(3)在铺层顺序的设计方面，基于工程材料数据库，可实现铺层顺序的快速组合与结果输出，明显提高了设计效率。