提升数学语言能力的两个维度：深度理解+清晰表达

高娟

[摘 要]数学语言是数学知识的重要组成部分，数学知识和数学思想方法终归要通过数学语言来表达，从而被理解和应用。因此，提升学生的数学语言能力对于数学学习具有重要作用。基于对数学语言的深度理解和清晰表达两个维度论述提升学生数学语言能力的基本路径，以提升学生的数学语言能力。

[关键词]深度理解;清晰表达;数学语言;小学数学

斯托利亚尔在《数学教育学》一书中指出，数学教学就是数学语言的教学。新课标指出，动手实践、自主探索与合作交流是学生学习数学的重要方式。而合作交流离不开数学语言。数学语言是一门特殊的语言，是数学交流的工具，是数学思维的重要载体。数学语言是由数学符号、数学术语和经过加工的自然语言等组成的一门语言，它是数学知识的重要组成部分，数学知识和数学思想方法终归要通过数学语言来表达，从而被理解和应用。因此，提升学生的数学语言能力对于数学学习具有重要意义。笔者从数学语言的深度理解和清晰表达两个维度论述了提升学生数学语言能力的基本路径，以期与广大教育同仁交流。

一、数学语言的深度理解

与生活语言相比，数学语言具有精准性、概括性和严谨性的特点。精准性主要体现在数学语言的条理性和准确性;概括性是指数学语言力图用简洁的符号和文字表达丰富的内涵;严谨性是指数学语言在逻辑上的有序性和严密性。由于数学语言具有以上特征，而学生的思维以形象思维为主，知识储备和认知经验不足，因此，学生在理解数学语言时会感到力不从心。其实，理解数学语言的过程就是学习数学的过程，也是发展数学思维的过程。基于此，在教学中，教师要注重采取多元化的教学策略，促进学生对数学语言的深度理解。

1.对关键字词的理解要准确无误

短短的一句话中可能蕴藏着丰富的信息，也可能蕴含着多个需要仔细推敲的关键字词。在教学中，教师要引导学生对关键字词进行追问和推敲，明确关键字词的含义，以及字、词、句之间的联系。只有这样，学生对数学语言的理解才会更加准确、更加丰实。

【“平行线”教学片段】

师：在同一平面内，不相交的两条直线叫作平行线。请同学们想一想，这句话中有哪些需要我们注意的地方？

生1：我们需要注意“在同一平面内”这几个字。

师：应该如何理解“在同一平面内”呢？

（学生讨论）

师（把两支铅笔交叉着放，使它们不接触）：这两支铅笔相交吗？

生2：不相交。

师：那这两支铅笔互相平行吗？

生3：不平行。

师：为什么它们既不相交也不平行呢？

生4：它们在的面不一样，一支在上面，一支在下面。

师（在黑板上画一组平行线）：这组平行线不也是一条在上面，一条在下面吗？

（学生陷入困惑）

（教师演示：在黑板上画了一条水平的直线，又在与黑板所在面垂直的墙面上画一条直线）

师：这两条直线相交吗？

生5：不相交。

师：它们互相平行吗？

生6：不平行。

师：与黑板上那组平行线相比，这两条线不但方向不同，而且不在同一个面内，一条直线在黑板这个面上，另一条直线在与黑板所在面垂直的墙面上。这说明，只有满足“在同一平面内”这个条件，不相交的两条直线才是互相平行的。

师：除此以外，还应该怎样理解“不相交”呢？

生7：说明不止有一条直线。

师：对。我们还要注意“两条直线”这个表述，平行线反映的是直线之间的相互位置关系，因此，不能单独说某一条直线是平行线。

教学中，教师以“平行线”的概念为例，通过引导学生斟酌“在同一平面内”“不相交”“两条直线”等关键字词，在理解的过程中，凸显了一个“准”字，不但使学生加深了对平行线概念认知的精准性，而且使学生体验到了数学语言的精准性和嚴谨性。

2.对句子的理解要注重辨析

数学语言具有很强的逻辑性，句式的变换、词句的颠倒都可能给句子的含义带来变化。这就要求学生在理解句子时，要对其中的逻辑关系进行推敲和辨析，准确理解句意。

【“圆锥的体积”教学片段】

教师引导学生通过实验得出：圆柱的体积是与其等底等高的圆锥的体积的 3倍。

在学生充分理解该结论的基础上，教师引导学生辨析“圆柱的体积是圆锥的体积的3倍，那么圆柱和圆锥一定等底等高”。有的学生认为这句话是对的，有的学生则认为是错的，并陈述理由：“比如，一个圆柱的底面积是6平方厘米，高是2厘米，那么它的体积是12立方厘米;一个圆锥的底面积是4平方厘米，高是3厘米，它的体积是4立方厘米。圆柱的体积是圆锥的体积的3倍，但是圆柱和圆锥既不等底也不等高。”教师由此引导学生得出结论：“圆柱和圆锥不等底不等高时，圆柱的体积也有可能是圆锥的体积的3倍。”

接着，教师进一步引导学生辨析“圆柱和圆锥等底不等高或等高不等底，那么，圆柱的体积一定不是圆锥的体积的3倍”。学生辨析：“圆柱和圆锥等底等高意味着它们底乘高的积也是相等的，但是圆柱和圆锥等底不等高或等高不等底时，它们的底乘高的积不相等，所以圆柱的体积一定不是圆锥的体积的3倍，因此这句话是正确的。”

教学中，教师引导学生深入剖析句式结构。通过辨析，学生认识到条件的改变、条件和结论的互换对语言表达所带来的影响，从而体验到数学语言的逻辑性和严密性，也增强思维的缜密性。

3.对不同形式的数学语言要灵活转换

数学中，各种量之间的变化关系通常是通过数学语言进行表达的。数学语言可以分为文字语言、符号语言、图式语言等，同一个数学结论可以用不同的数学语言表达出来。学生解决数学问题的过程，实质上就是将不同形式的数学语言进行转化的过程。因此，在教学中，教师要引导学生对不同形式的数学语言进行灵活转换。

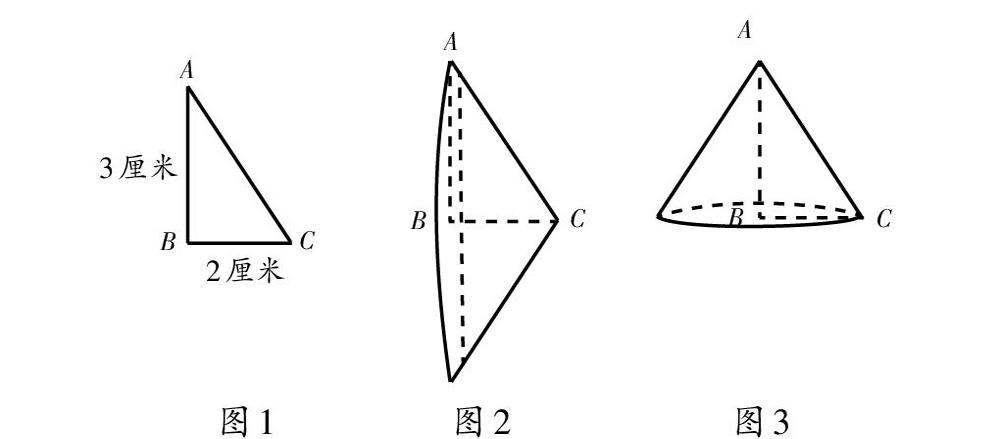
【题目：直角三角形ABC（如图1）的两条直角边的长度分别为2厘米和3厘米，以两条直角边所在的直线为轴分别旋转一周，得到两个圆锥，哪个圆锥的体积大？】

在遇到这样的文字表述题时，教师要引导学生把文字语言转化成图形语言，使学生明确一共有两种旋转方式：一种是以3厘米的直角边所在直线为轴进行旋转，另一种是以2厘米的直角边所在直线为轴进行旋转（如图2、图3）。

教学中，教师指导学生按照题目意思把文字语言转化成图形语言，从而使数量关系变得更加直观生动。在这个过程中，一定要注意不同形式的数学语言之间转化的不变性。

二、数学语言的清晰表达

要提升学生的数学语言能力，就不能仅局限于锻炼学生对数学语言的深度理解，还应当使学生在“说数学”中逐步提升数学语言的表达能力。

1.表达要注重有序

表达有序实际上强调的是思维有序。数学语言本身具有很强的逻辑性，这就要求学生在进行数学表达时要有清晰的思维，如果学生的思维比较混乱，那么其数学表达必将是无序的。教学中，教师要给予学生足够的时间，以提升学生数学表达的有序性。

【“凑十法”教学片段】

教师引导学生用自己的语言说一说什么是“凑十法”。一名学生说道：“‘凑十法就是先凑成10，比如9+6，先算9+1=10，也就是从6里面拿出了1，然后再算10+5=15，也就是用10加上剩下的5。”短短的一句话，就把“凑十法”的本质描述出来了。

教学中，学生的数学表达都凸显了有序性，这实际上体现了学生思维的条理性。然而，要把这种内隐的思维条理性转化成外显的语言有序性，还需要教师在日常教学中对学生的数学语言表达能力进行训练。

2.表达要注重简约

用数学语言描述数学问题要注重详略得当、简洁明了。必须交代的事项要表达准确，尽量避免重复或多余的叙述。这就要需要学生在数学表达时講究方法，抓住核心，力求简约。

【判断题：半圆的周长是所在圆周长的一半】

学生只需清楚表达两点：一是“半圆的周长”包括圆周长的一半再加上这个圆的直径;二是 “半圆的周长”为什么要加上圆的直径，能够从“只有封闭图形才有面积”这个角度进行论述即可。学生只要明确了这两点，就能正确解决这个问题。

数学语言不在多，而在精。在这一道题中，学生的表达不但清晰有序，而且精练，抓住了问题的核心，通过寥寥数语从本质上把握了问题。

语言是思维的外壳。语言的准确性体现思维的周密性，语言的层次性体现思维的逻辑性，语言的多样性体现思维的丰富性。对数学语言的深度理解和清晰表达是提升学生数学语言能力的重要维度。在教学中，教师要鼓励学生大胆表达，使学生乐于表达、善于表达，提升数学语言能力。

（责编 黄 露）