他山之石:ICME-14“问题提出”研究观点综述与教学启示分析
2021-09-30闫佳洁于国文
□闫佳洁于国文
一、引言
第14届国际数学教育大会(ICME-14)的专题研究组聚集了国际上共同关注的62个专题,问题提出与问题解决共同构成了第17个专题研究组(TSG17),其主题为数学教育中的问题提出与问题解决。在为期一周的ICME-14会议中,来自美国、德国、意大利、巴西等13个国家的研究者共同聚焦问题提出的研究,呈现了4场精彩纷呈的、具有国际视野的问题提出学术交流盛宴。为了更好地借鉴国际经验,推进我国关于数学问题提出的研究,本文聚焦ICME-14中各国在问题提出方面的经验,进行详细分析,以期对我国问题提出的研究提供一定的借鉴。
二、问题提出研究的关注点
TSG17四场专题报告,包含37个报告,其中以问题提出为主题的报告有24个,这24个报告关注的核心是某一场域下的问题提出、问题提出的表现研究、问题提出的诊断功能、问题提出的过程以及问题提出的教学策略这5个方面。
(一)某一场域下的问题提出
问题提出的基本场域是问题提出得以发生的活动背景和资源条件。此次会议中,来自多国的研究者关注到了不同场域下的问题提出,如教科书中的问题提出、问题解决中的问题提出、WalkSTEM项目中的问题提出、现实情境中的问题提出等。其中教科书中的问题提出十分具有中国特色,一项关注教科书中问题提出的历史发展[1],一项关注不同学段下问题提出在教科书中的进阶设计[2]。此外,正如中国学者郑培珺所说,要关注问题情境的创设,好的问题情境能够揭示数学知识内部的矛盾和联系,激发学生的内在动力[3]。
德国学者Luisa-Marie Hartmann等人认为,应该给予现实世界中的问题提出更多的关注,当学生在现实世界中提出问题时,实际上是学生自己在现实世界的元素间构建网络的过程,在这个过程中,学生提出了真实的问题。基于此他们采用6个现实情境任务调查学生的问题提出表现[4],在ICME-14会议上,重点报告了借助运动场的真实情境考察学生问题解决能力的案例,他们运用该现实情境对德国的82名学生进行了测试,研究结果发现,在真实的世界中,虽然学生提出的大多数数学问题都是显而易见的(70%),且多为封闭的(94%)问题,但是提供真实世界的信息可以激励学生提出与现实相关的问题[5]。
美国学者Min Wang等人介绍了美国Walk-STEM项目中的问题提出活动,WalkSTEM是美国都市区的一项倡议,学生、教师、家长在建筑、艺术和自然中寻找数学概念和原理,证明数学无处不在。Min Wang等人关注学生在WalkSTEM课外活动期间提出的数学问题。学生(8~10岁)第一次看到图1时,提出的问题是:“它们不像是弯曲的,但为什么会这样?”再次看到图1时,提出的问题是:“圆顶上有多少个三角形、圆形,有多少根长条?”随后当学生在学校走廊中看到由方形地砖铺成的地面时,提出问题:“地面上有多少个小方块?”这是对图1问题情境思考的迁移。此后,学生关注到了更多的几何形状,如六边形、平行四边形和菱形等,还注意到了建筑物结构中的数学问题[6]。

图1 测地圆顶
可见,问题提出的活动背景和资源条件可以非常丰富,上文提到的WalkSTEM项目中的场域和现实世界的场域都关注问题情境的真实性,且学生在真实情境中的表现有趣而富有价值,这些真实情境一边牵动着学生的生活经验和直观感知,另一边联结着学生的数学知识和概念思维,这两者的融合是学生提出真实的、有价值的问题的必要条件。
(二)问题提出的表现研究
问题提出的表现研究是此次会议中问题提出的重要议题之一,多位研究者报告了对学生以及职前、在职教师问题提出表现的研究,这些研究既有民族特色,又有跨国比较,还有纵向研究。我国学者张丹等人对小学四年级学生进行了为期3年的追踪研究,直到他们六年级毕业,并在ICME-14会议上重点报告了一年内学生问题提出的表现变化,以经典的问题提出任务——铃声问题为例,一年后学生的问题提出平均表现和学生的数学毅力均优于一年前,有明显的增强趋势[7],铃声问题如下:
在一次聚会中,客人随门铃声进入会场。
第1次铃声:1个客人进入会场。
第2次铃声:3个客人进入会场。
第3次铃声:5个客人进入会场。
第4次铃声:7个客人进入会场。
……
这样继续下去,后一次铃响时进入的客人总是比前一次铃声时进入的客人多2个人[8]。
我国学者董连春等人关注了少数民族地区五年级学生的问题提出表现,通过3个问题提出任务和学生的数学成绩收集数据,并进行了数据分析,发现汉族学生比少数民族学生能提出更多的数学问题,但数学问题提出能力并无明显差异;女生比男生更有意识和能力提出数学问题;女生在灵活性和创新性问题上普遍优于男生;数学问题提出能力与其数学成绩呈显著正相关[9]。
美国学者Fenqjen Luo则关注跨国研究,比较中美两国五年级学生的数学问题提出表现,以除法知识为例,该研究发现中国学生比美国学生提出问题的结构更丰富[10]。上述研究均关注学生的问题提出表现,Sintria Lautert等人则关注教师的问题提出表现,发现中小学教师很难用乘法或除法的概念或结构提出复杂或具有挑战性的问题,并说明教师需要进行问题提出的相关培训[11]。
林林总总的对于问题提出表现的研究揭示了研究者从单一被试的问题提出研究走向多元化的趋势,并渴望开启比较研究,关注不同团体问题提出表现的差异性和共性,从而为问题提出的教学提供精准的指导。
(三)问题提出的诊断功能
问题提出被认为是发现概念理解错误及原因的良好诊断工具,也是深入理解数学概念的工具。Siegler等人发现,可以根据10岁儿童的分数知识预测他们16岁时的代数知识和整体数学成就[12],在此次会议中,关注问题提出的诊断功能的研究也都以分数知识为载体。姚一玲和蔡金法运用问题提出探究职前教师对分数除法概念的理解,研究结果表明,几乎所有被试者在分数除法的计算问题上均不存在问题,但很大比例的职前教师表现出对分数除法的程序理解优于概念理解[13]。至于职前教师在分数除法的概念理解上存在什么问题,该研究并没有进一步阐述。
土耳其学者Tuba Iskenderoglu则通过问题提出研究教师在分数加法方面存在的困难,该研究对31名小学数学教师进行了问题提出测试,分析教师的回答,发现教师在分数加法中存在的主要困难涉及假分数的加法,困难较少的涉及两个真分数相加知识的问题提出任务[14]。可见,教师在分数加法教学中存在的困难与知识的难易程度是一致的。此外,Eda Vula等人探究了问题提出策略对数学知识理解的影响,具体来说,他们研究了101名职前数学教师的问题提出策略对分数概念理解的影响,两周的教学干预后,通过前测和后测的对比发现,问题提出策略会影响职前教师对分数概念的理解和表征分数的能力,并建议开展问题提出活动的培训以提高职前数学教师的问题提出能力[15]。
上述研究生动地体现了问题提出具有诊断功能,在诊断被试者对某一数学概念或知识的理解程度、存在困难等方面具有较强的作用和功能,ICME-14中的关于问题提出的诊断功能多用于职前或在职教师,借助问题提出诊断学生数学知识的理解程度对教师的教学大有裨益,值得被关注。
(四)问题提出的过程
目前,大多数关于问题提出的研究都较为关注问题提出的结果,并以提出的问题来判断学生或教师的问题提出表现。事实上,问题提出是学生数学思维流动的过程,仅从问题提出的结果评价学生是不全面的,还应该关注学生问题提出的过程。在此次会议中,来自新加坡、德国等国的研究者关注了问题提出的过程,并与参会者分享了他们已有的研究成果。
新加坡学者Puay Huat Chua将Polya(波利亚)提出的著名的问题解决的四个步骤与问题提出相对应,从认知调节视角提出了问题提出的四个阶段,分别是关注特征与条件、问题建构、尝试解决、回顾。Puay Huat Chua通过出声思考观察Tan提出问题的过程,以此来检验学生提出问题的过程是否符合这四个阶段,研究发现,前三个阶段是学生较为明显经历的过程,且前两个阶段最为明显,回顾在学生问题提出的过程中表现出来的较少[16]。
德国学者Lukas Baumanns等人较为细致地描述了问题提出的过程,分别是分析、改变、生成、问题解决和评估。对34个学生进行研究,运用口语报告分析法观察学生问题提出的过程,发现学生问题提出的过程并没有遵循明显的顺序性规律,但问题解决和评估过程常常交织在一起(见图2)[17]。我国学者张玲等人在对问题提出中的数学交流进行研究时,也关注了问题提出的过程,并将其分为三个阶段,分别是输入阶段、加工阶段、输出阶段,分别代表理解任务、建构问题和表达问题[18]。

图2 问题提出的过程
对问题提出过程的研究价值深远,因为问题提出与其说是为了结果,不如说更关乎过程。作为问题的结果,其背后承载的实际上是在提问过程中的学习者的思考与好奇,是其经验与知识的具体化。上述对于过程的研究正体现了提问者的数学思维和知识具体运用的过程,更加明晰了提问者是如何提出问题的。
(五)问题提出的教学策略
对问题提出的研究以培养学生的问题提出能力,促进学生的创新意识和创造力提升为目标,因此如何培养学生的数学问题提出能力就显得十分重要。此次会议上,多位研究者聚焦问题提出的策略与方法,致力于提升学生的数学问题提出能力。Miguel Cruz Ramírez受Brown和Walter的“What-ifnot”策略的影响,提出了名为“SCASV+T”的启发式问题提出教学策略,其基础策略实施的顺序为:选择、分类、联系、探寻和表征,在此基础上,还可以进行下一步进阶策略,即转换,该策略是针对分类、联系、探寻这三阶段实施的。
此外,我国学者张丹提出了问题提出的教学模式,包括情境体验、问题产生、问题解决和反思总结,这四个阶段形成了一个循环(如图3),且在问题解决和反思总结的过程中均可能产生新的问题,该模式强调问题提出教学应该注重营造宽松互动的氛围,设计学生沉浸的情境,梳理整合提出的问题,激发思考形成问题链,组织实践与合作交流,学习支持与激励评价[19-20]。
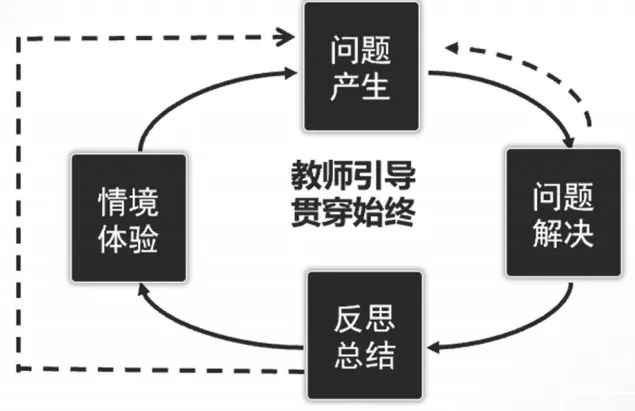
图3 问题提出教学模式
上述具体而系统的问题提出教学策略与模式给问题提出教学提供了基本的方向与垫定了基础,这一研究在教学中发芽,也在教学中生根,对学生问题提出能力的影响是深远的,正因为如此,也需要进一步在实践中检验和修订。
三、对我国问题提出研究的启示
与问题解决相比,数学问题提出是数学教育中一个年轻得多的探究领域。尽管近几十年来对这一领域的关注迅速增长,许多国家的课程文件已将问题提出作为教学重点,但目前关于问题提出的研究还不够深入,既缺乏系统性,也缺乏对话与沟通。ICME-14会议上来自各个国家的研究者报告了问题提出最新的研究进展,这也为我国问题提出研究带来了新的思考和启示。
(一)关注真实情境下的问题提出
在此次会议中,不同场域下的问题提出是研究者关注的话题之一,其中真实情境下的问题提出最受欢迎。以往对问题提出的研究更多关注的是问题情境的开放程度,例如,大多数研究者运用Stoyanova对问题情境的划分,即对自由、半结构化和结构化的问题情境进行研究,现在一些研究者更多地关注情境的真实性,使生活经验和知识基础融合,让学生在真实的情境中触动思维,建立联系,对于提问者而言,这是提出真问题的沃土,需要在问题提出研究中引起关注。
(二)关注问题提出的比较研究
ICME-14会议中的报告和壁报展示都说明多个国家的研究者正在共同关注问题提出的研究,且已有研究者洞察到比较不同国家学生问题提出表现的研究是必要的,此外,也有研究比较少数民族学生和汉族学生的问题提出表现差异。这给我们启示,不仅要关注具有共同特征的学生的问题提出表现,还要关注不同团体问题提出表现的差异性,如男女生之间的差异、不同年级之间的差异、不同民族之间的差异、不同国家学生之间的差异等,在比较研究的基础上,启动对话,互相促进。
(三)关注问题提出如何促进知识理解
问题提出的诊断功能已被我国和其他国家研究者共同关注,并通过问题提出测试来诊断教师和学生对数学知识的理解,目前大部分问题提出用于判断被试者问题提出的表现和对数学知识的理解程度。在此次会议中,问题提出也被用于判断被试者数学知识理解存在的困难,以及通过问题提出培训对教师的数学知识理解产生的影响,在问题提出诊断功能的基础上,关注问题提出如何促进数学知识的理解是需要进一步关注的研究方向。
(四)关注问题提出的过程
前三个方面或从较为宏观的视角探究问题提出,或从问题提出的产物——问题的角度来研究问题提出,对问题提出的过程还缺乏深入的研究,由于对问题提出的过程知之甚少,也使得问题提出教学存在一定的困难。此次会议上,对于问题提出过程的关注启示我们对问题提出的研究要从宏观走向微观,进一步探究问题提出的过程是数学教育研究者亟须关注的问题。而对于问题提出过程的研究也应从着眼于某个切面的即时过程转向持续跟踪研究之下对于思维进阶的刻画,以问题提出的过程体现学生问题提出的发展路径。
(五)关注问题提出的教学
问题提出研究的最终落脚点是发展学生的问题提出能力,因此问题提出教学就显得尤为重要。ICME-14会议上,来自各国的研究者将目光聚焦于如何通过对问题提出教学策略、模式及方法的研究来促进学生问题提出能力的提升,这也启示我们关注问题提出教学,以培养学生问题提出能力为生根点和目标,探寻和实践合适的、有益于学生问题提出能力发展的教学模式。
四、结语
问题的产生或源于好奇,或源于思考,无论如何,它们对儿童的成长都是弥足珍贵的!ICME-14会议上关于问题提出的学术交流盛宴为我们继续研究问题提出的策略提供了思考,同时诸如如何启发儿童灵动的思维,把源于好奇的、生动的困惑与数学知识关联起来,浓缩为有意义的数学问题等等仍然还没有答案,需要我们继续探寻和研究。
