斜拉索人行天桥承载力研究
2021-09-30杜明阳闫啸坤
杜明阳, 闫啸坤
(国能朔黄铁路发展有限责任公司,河北 肃宁 062350)
随着现代化城市建设的进行,越来越注重城市的人文环境。新建的人行天桥除了满足行人的基本功能外,更加注重桥梁的美感,从而使得其成为地标性建筑。在这样的背景下,新型的结构形式如雨后春笋,层出不穷。为了保证新建人行天桥的安全性能,更应该强调桥梁的设计环节[1-11]。
陈程[2]从拱桥的概念、特征、发展历程等方面对其进行了较为系统的阐述,并分析了刚度比、矢跨比等参数改变对拱桥整体受力性能的影响,提出依据拱桥刚度比对系杆拱桥的分类标准。李丰群等[3]详细介绍了南京太平北路人行天桥的设计特点和创新,该桥采用桅杆式斜拉桥形式,从而减小了天桥的长度,使得结构更加合理,同时在造型上给观众以轻盈、通透的美感。石春龙等[4]以长春新区月亮拱景观人行桥为研究对象,分析了结构自重、风荷载、温度荷载等荷载作用,对其主梁、拱肋受力性能的影响。研究结果表明该结构满足要求,为类似工程提供了参考。刘军[5]以张家口清水河工业南桥复建工程为研究对象,分析了桥梁不同阶段、不同荷载组合下的受力性能,并对其整体稳定性进行了分析研究。刘钊等[6]通过对不同形式系杆拱桥分析研究发现,网状系杆拱桥的受力性能优于竖吊杆体系拱桥,主要表现在其拱肋和吊杆的弯矩值较小。陈列等[7]以128 m系杆拱桥为主要研究对象,分析了矢跨比、吊杆布置形式、刚度比等参数对其受力性能的影响,其研究结果表明,采用柔性吊杆网状体系布置时,结构的受力性能最好。
本文以朔黄春霖路人行天桥为研究对象,在检查过程中,发现其中一根斜吊杆失效,并对相邻吊杆的受力形成影响。研究斜吊索人行桥在满足标准荷载作用下,其整体强度和稳定性是否满足要求,及吊杆失效对其受力性能的影响。
拱桥作为一种优美的桥型,越来越多被采用。作为其主要受力构件的吊杆,其受力性能直接关系到桥梁的安全性能[9]。在使用过程中,由于使用维护不当导致吊杆的失效或者更换,例如英国Wye桥、中国广州海印桥、乐山岷江大桥、广东鹤山九江桥、红水河桥等均发生了吊杆断裂事故,为了明确吊杆失效对桥梁、拱肋、吊杆受力性能的影响,研究人员开展了相关研究。Mozos et al[12]通过数值模拟和试验的方法分析了斜拉索失效对斜拉桥受力性能的影响。夏欢等[13]分析了不同位置吊杆失效对拱桥受力性能的影响。Zhou et al[14]等分析了断索对斜拉桥受力性能的影响,研究中考虑了斜拉索的初始装填、斜拉索的非线性特征、荷载的组合形式等因素的影响。陈文明等[15]分析了单根拉索失效时对结构受力性能的影响,研究结果表明,当结构的内力较大导致拉索失效后,其索力将分配到其他拉索中,这种情况增大了其他索断裂的可能性,从而有可能引发结构整体的坍塌。赵金钢等[16]结合工程案例,利用有限元的方法,分析了吊杆失效对结构的影响,研究结果表明,单根吊杆失效时,对结构的影响较小,当断裂的吊杆超过3对时将会对拱肋部分造成明显破坏,增加结构整体破坏的可能性。王兆铭等[17]以某在建大桥为主要研究背景,分析了不同位置吊杆失效对结构受力特性的影响,研究结果表明,单根吊杆断裂时,对同侧吊杆影响较大,但是各吊杆的受力性能仍在其工作范围内,所以对结构的整体稳定性的影响可以忽略。不同位置吊杆断裂,其影响程度存在明显差异,四分点吊杆断裂时影响最大。本文以朔黄春霖街天桥为对象,开展了相关研究。
1 结构概况
1.1 工程背景
春霖路人行天桥主桥采用(21.5 m钢梁+60 m提篮拱加劲+21.5 m钢梁)连续梁,提篮拱矢跨比取1∶6.8,桥面有效通行宽度3.0 m。边跨采用纵横梁形式,纵梁为双边主梁,采用箱形截面,内倾8°。中跨60 m,跨越春霖路,为提篮拱加劲梁形式;拱肋及主梁均为箱形截面,拱面内倾8°;斜拉索(拉杆)纵横向均倾斜(中拉杆仅横桥向倾斜),呈扇形布置;2拱片间设3道横撑,形成整体结构,如图1所示。
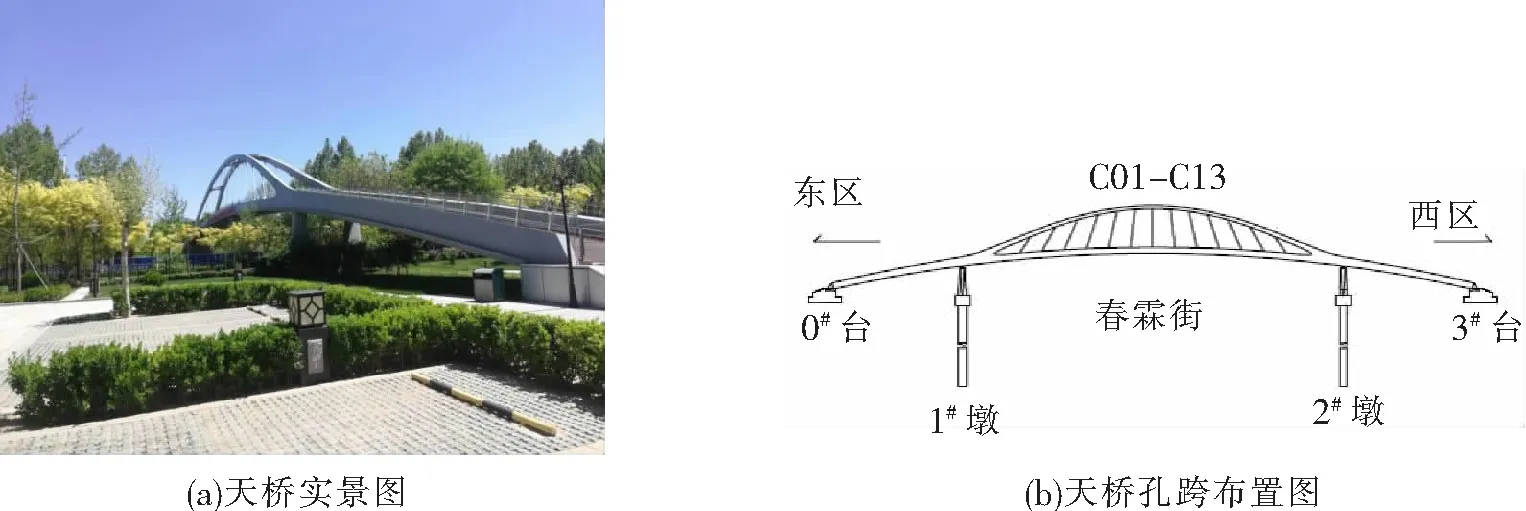
图1 春霖路人行天桥
边纵梁采用Q345qD钢梁,截面采用箱型,顶底板及腹板均厚20 mm,等宽度350 mm,变高度,腹板内倾8°。中跨钢箱梁标准高度为1 m,边跨钢箱梁高度由1 m变高到1.4 m。拉索采用叉耳双向螺杆型拉索,通过耳板(横隔板)分别与主梁及拱肋连接。拉索布置形式采用扇形布置。桥墩基础均采用钻孔灌注桩基础,桥台基础采用扩大基础型式。
1.2 有限元模型介绍
采用MIDAS桥梁专业分析软件建立全桥模型,分析桥梁结构受力状态,有限元模型中主梁结构采用板单元,吊杆结构采用桁架单元模拟,根据现场检查情况,主桥状态完好,未见明显的结构损伤,计算板厚及截面直接采用设计截面,未考虑截面尺寸的磨损,边界条件与实际情况保持一致,建立的有限元计算模型如图2所示。

图2 有限元计算模型
1.3 荷载说明
1.3.1 永久荷载
结构自重:主梁计入自重,以及二期恒载的质量。
自重:钢材容重取78.5 kN/m3,考虑焊接等因素,自重调整系数取1.1。
二期荷载(包括桥面铺装、玻璃幕墙及照明等):2.7 kN/m2。
1.3.2 活载
人群:纵向整体计算取5.0 kN/m2。
风荷载:依据《城市人行天桥与人行地道技术规范》,风速取32.57 m/s,全桥装饰后挡风面积(含玻璃幕墙)是结构设计挡风面积的1.35倍,风荷载计算时按结构设计面积施加时考虑1.35倍放大系数。纵向风压按横向风压的0.4倍取值。横向风压
W=K1K2K3K4W0
(1)
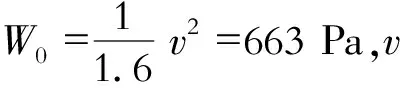
根据式(1)计算可以得到横向风压为586.1 Pa。
横向风压施加值为:1.35×586.1=791.2 Pa。
纵向风压施加值为:0.4×586.1=234.4 Pa。
强度及稳定计算荷载组合采用基本可变荷载(人群荷载)设计值、永久荷载(自重)设计值与其他可变荷载(风荷载)设计值相组合。
其中永久荷载组合系数取1.2,可变荷载组合系数取1.4,可变荷载组合值系数取0.75。
2 结构受力分析
2.1 整体强度分析
天桥上部结构在成桥状态下,在结构自重、人群荷载、风荷载的作用下,主梁的应力分布相对合理,绝大多数位置的应力在70 MPa左右。在局部位置出现应力集中现象,最大von-Mises 应力为101.0 MPa,出现在支座处拱肋顶面迎风侧位置。虽然其值为最大值,但是从结构强度出发,结构具有较大的安全储备,仅为设计标准的34.7%(fd=270 MPa),表明主梁整体强度满足要求。
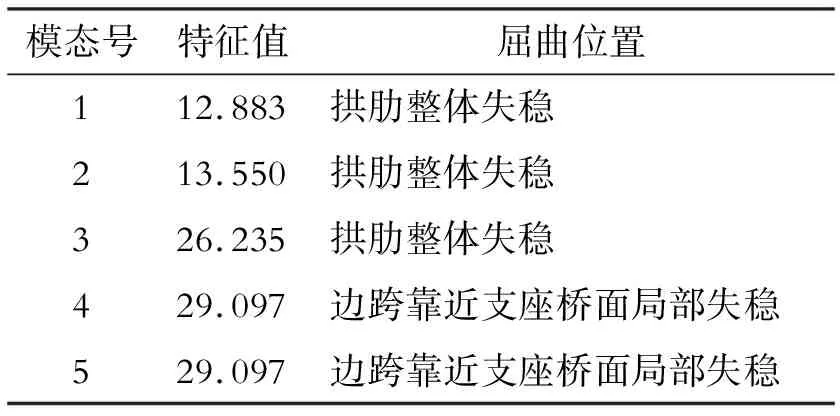
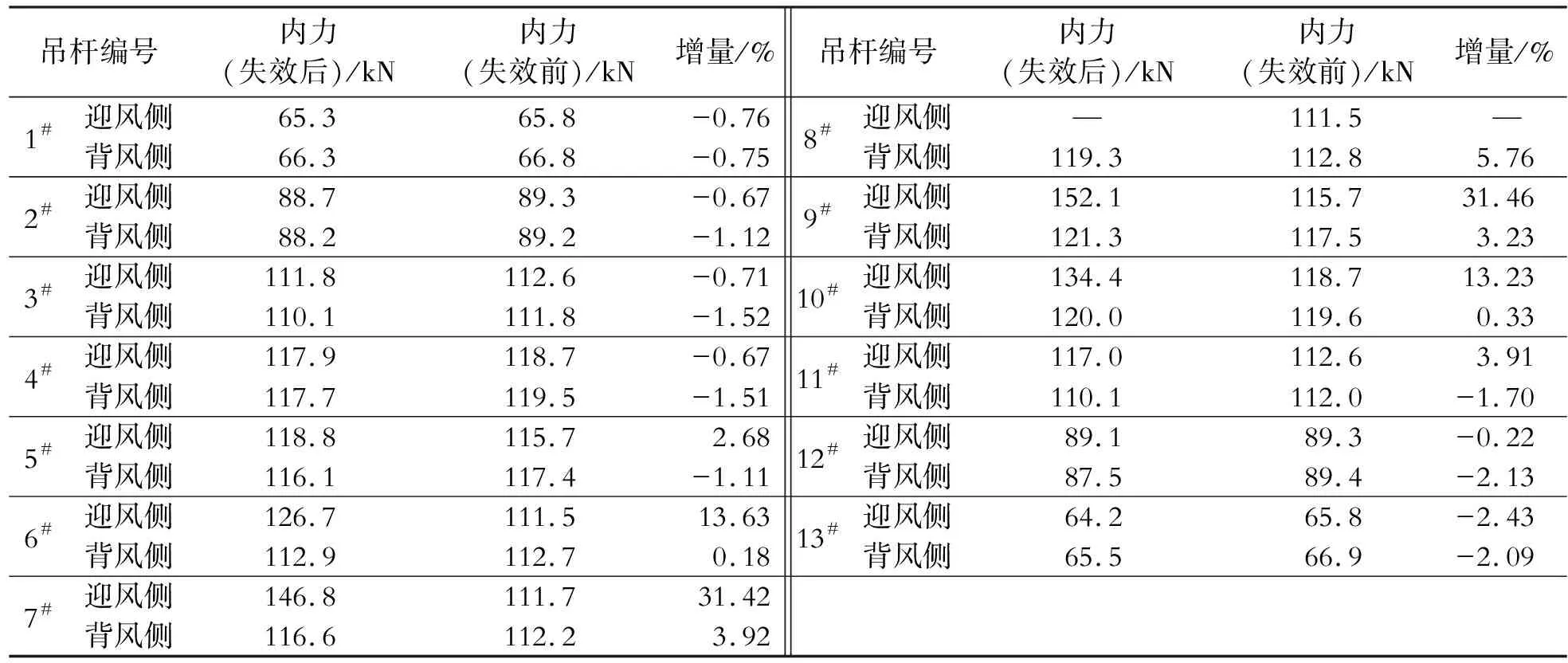
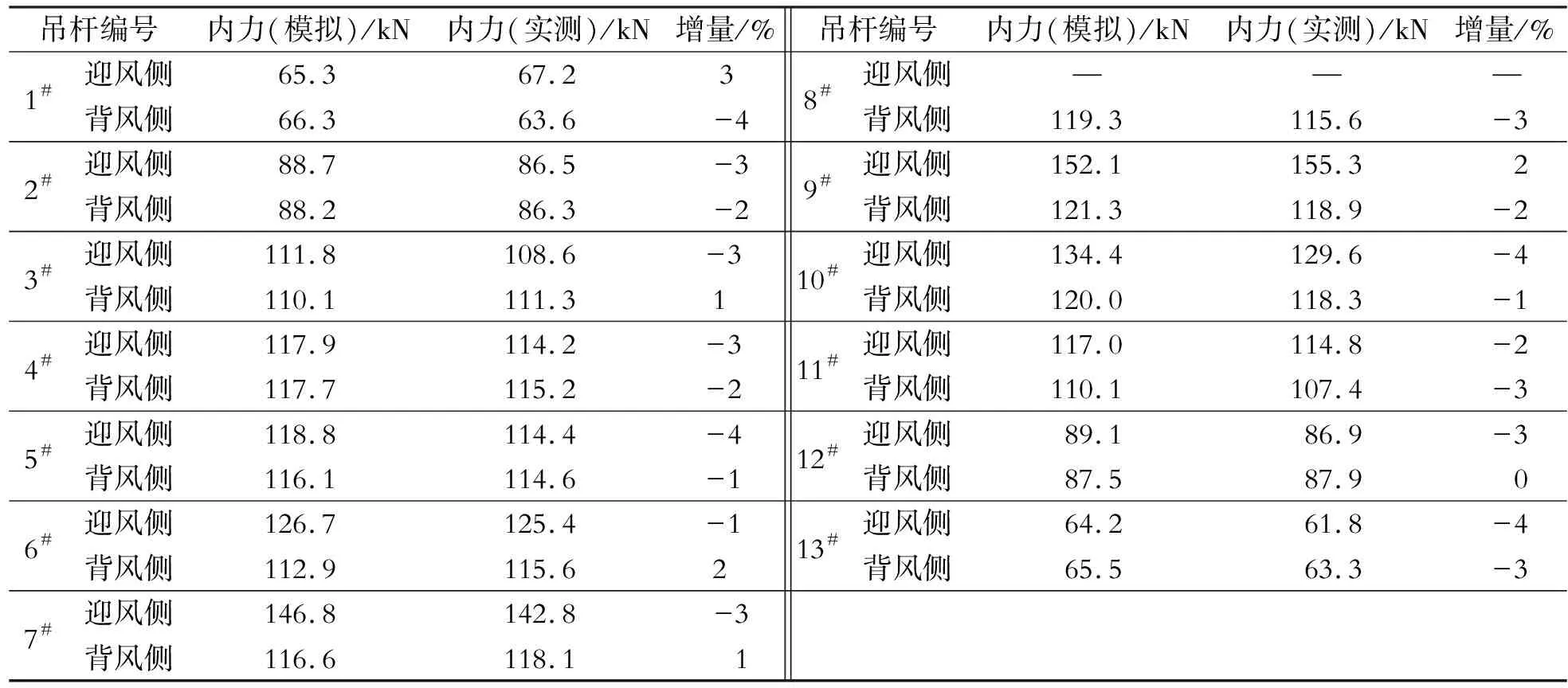
天桥上部结构在基本组合下,绝大多数位置的剪应力在40 MPa左右,分布较为合理。与von-Mises 应力情况相似,也存在应力集中的现象,最大剪应力为56.8 MPa,同样也出现在支座拱肋顶面迎风侧位置,最大剪应力为设计标准的36.7%( 为了明确人行桥整体稳定的特征,进行了相关研究,整体稳定分析计算时按照弹性分析,结构自重及二期按恒载考虑,荷载系数取1.2,人群荷载按可变荷载考虑,荷载系数取1.4。通过相应的有限元计算得到前五阶模态的屈曲系数,具体数值如表1所示。从表1可以看出,桥梁整体稳定性主要与拱肋的稳定性相关,最小屈曲系数12.883、最大屈曲系数为29.097,满足稳定性要求。前三阶屈曲主要是拱肋的整体屈曲,前四阶屈曲模态见图3。 图3 天桥上部结构屈曲分析结果 表1 前五阶屈曲系数计算 人群荷载作用下,主梁的最大位移发生在桥梁的跨中位置,最大竖向变形为17.4 mm。根据主梁最大跨度60 m,容许变形值为:L/800=60 000/800=75 mm,最大竖向变形为17.4 mm远小于主梁的允许变形值,所以结构变形满足要求。 桥梁在运维过程中,如果养护不当,可能造成局部导杆的松动。与之类似在吊杆更换的过程中,会对局部吊杆进行拆除。这两种情况发生时,势必会造成吊杆内力重分布。在进行朔黄春霖街天桥检测过程中,发现8#吊杆出现松动,为了明确吊杆失效对结构受力性能的影响,有必要开展相关研究。研究过程中考虑了一种极端状态,即认为8#吊杆完全失效,在这样的背景下建立Midas模型,分析了单根吊杆失效后对桥梁结构强度、刚度稳定性的影响,同时也考虑了单根吊杆失效后对其余吊杆内力的影响。 单侧8#吊杆失效后,主梁在基本组合下,最大von-Mises 应力为101.4 MPa。吊杆失效后桥梁的最大von-Mises 应力增加约0.4 MPa,增幅很小,没有明显影响,且其最大应力值远小于材料的允许影响,表明结构存在足够的安全储备。同时也观测到最大应力出现的位置也出现在支座处拱肋顶面迎风侧位置。因此可以认为单根吊杆失效后,对主梁应力分布的影响不明显,未造成最大应力分布位置发生改变,因此可以忽略单侧8#吊杆对上部结构强度的影响。 单侧8#吊杆失效后,天桥竖向变形在单侧8#吊杆失效时,最大变形为17.9 mm。失效后,主梁的最大变形仅仅增加了0.5 mm,增幅约2.9%,因此可以认为主梁最大变形增加不明显,在该条件下,上部结构的最大变形仍远小于允许变形。这表明单根吊杆失效后对桥梁结构强度的影响可以忽略。 单侧8#吊杆失效时,天桥吊杆内力在基本组合作用下的内力计算结果(不考虑张拉力)如表2所示。从表2可以看出,单根吊杆失效后,其同侧相邻吊杆的内力改变最为明显,例如7#吊杆和9#吊杆的内力较8#吊杆失效前分别增加了31.42%和31.46%。随着吊杆位置远离,吊杆失效对其影响逐渐减弱,例如,6#吊杆和10#吊杆的内力较8#吊杆失效前分别增加了13.63%和13.23%。随着吊杆位置的继续远离,其内力增加小于5%,8#吊杆失效对其影响可以忽略。同时也观测到迎风侧8#吊杆失效后,与之相对应的背风侧的8#吊杆的内力仅增加了5.76%,对背风侧其余吊杆的影响更小,因此认为吊杆失效后,对侧吊杆的内力改变不明显,对其影响可以忽略。这与相关文献中的结论相一致。 表2 吊杆内力计算对比表 为了明确吊杆失效对桥梁结构稳定的影响,对比了单侧8#吊杆失效前后,结构前五阶屈曲系数的分布规律,具体数值分布如表3所示。从表3可以看出,单根吊杆失效前后结构的屈曲系数变化不明显,例如第一阶屈曲系数失效前为12.883,失效后增大为12.940,增加了0.4%,改变非常小,可以认为结构的屈曲模态在失效前后基本相同,未发生改变。因此得到结论,单根吊杆失效对整体稳定性的影响可以忽略。 表3 前五阶屈曲系数计算对比 为了验证数值模拟的计算结果,检验桥梁的真实工作状态,采用频率法对朔黄铁路人行天桥索力进行测试,索力测试过程中出现个别索力实测值与数值模拟结果相差较大,采取多次测试并根据实际吊索约束条件来进行索长调整,多次测试结果修正值见表4。 表4 吊杆内力对比表 通过Midas有限元模拟,对朔黄春霖街天桥的主梁和吊杆进行了强度和稳定性分析,并考虑了吊杆失效对结构强度、刚度和内力的影响,得到了如下结论: (1)该天桥在永久荷载、活载的设计荷载组合作用下,结构最大拉应力仅为材料允许强度的34.7%,剪应力仅为材料允许强度的36.7%,表明材料强度满足要求,且有较大的安全储备。针对结构稳定性研究发现,其最小屈曲系数为12.883,表明结构不会发生屈曲破坏。在标准荷载作用下,结构的最大变形为17.4 mm远小于限制70 mm。综上所述,可以认为在标准荷载作用下该桥强度、刚度和稳定性满足要求,且具有较大的安全储备。 (2)8#吊杆失效时,同侧吊杆的内力改变较为明显,相邻2根吊杆的内力增大了30%左右。随着吊杆位置远离失效吊杆,其受到的影响逐渐减小。异侧吊杆受其影响较小,与之相对应的吊杆的内力仅增大了5.76%,远小于同侧相邻吊杆受到的影响,因此可以忽略吊杆失效对异侧吊杆内力的影响。 (3)单根吊杆失效后,主梁在基本组合下,桥梁的最大von-Mises 应力增加约0.4 MPa,增幅很小没有明显影响。天桥竖向变形在单侧吊杆失效后,主梁的最大变形比失效前增加了0.5 mm,增幅约2.9%,主梁最大变形增加不明显。 (4)单根吊杆失效后对结构整体强度、刚度和稳定性的影响不明显,可以忽略。在设计中应该适当增加结构的安全储备,防止吊杆失效后造成的吊杆内力的二次分配对相邻吊杆产生破坏。 (5)模拟结果一定程度上能够反映结构的受力特征,当索力测试过程中出现个别索力实测值与数值模拟结果相差较大,应采取多次测试并根据实际吊索约束条件来进行索长调整,在实际工程中应该注意。2.2 整体稳定性分析

2.3 上部结构刚度分析
3 吊杆失效结构受力分析
3.1 吊杆失效对上部结构强度的影响
3.2 吊杆失效对上部结构刚度的影响
3.3 吊杆失效对内力的影响
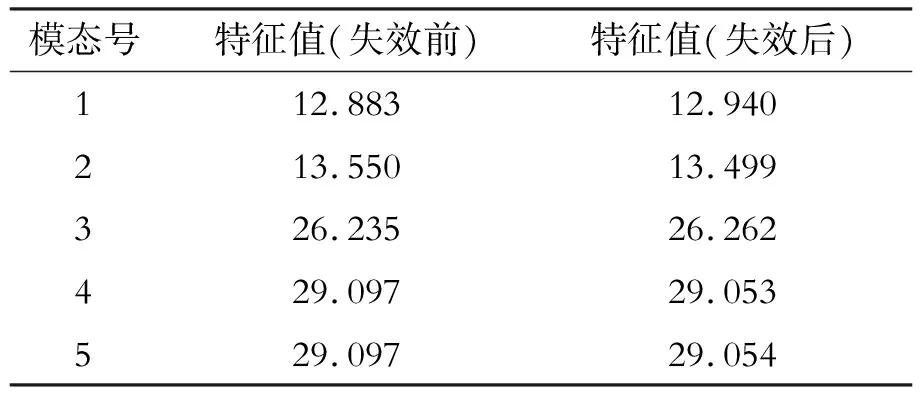
3.4 吊杆失效对稳定性的影响
4 桥梁结构承载能力测试
5 结论
