基于ABAQUS对抗滑挡墙结构的优化设计研究
2021-09-29舒天白任伟中符贵军高开丰张基鹏
舒天白 任伟中 符贵军 高开丰 张基鹏
(1.绍兴文理学院 土木工程学院,浙江 绍兴 312000;2.中国科学院武汉岩土力学研究所,湖北 武汉 430071)
0 引言
我国地形分布西高东低,呈现三级梯状,中西部地区多山,地质灾害频发,给人民的生命财产带来了隐患.科学高效地治理边坡滑坡等问题成为很多科研人员研究的重点.姚燕明等[1]就微型桩基挡土墙的抗滑稳定性方面进行了离心试验模拟研究,得出微型桩对软土地基有较好的抗滑阻流稳定作用的结论;赖鹏晖[2]利用数值软件对不同加筋土挡墙结构的应力变形和加固机理进行了对比;张智超等[3]对微型桩与加筋土挡墙的工作机制进行了检验探讨,并对微型桩加固前后加筋土挡墙在多级附加荷载下的静力响应进行对比研究;张智超等[4]就加筋土挡墙的变形特性展开研究,对其影响因素进行了分析;王祥任等[5]探讨了微型桩的特点、结构形式和桩与地基的承载力的计算,并在某工程实例中探讨了微型桩挡墙的优化方案;瞿永等[6]基于对微型桩的研究,归纳出微型桩挡墙结构的设计方法,并在工程实际中验证了方案的可行性;唐晓松等[7]运用有限元强度折减法搜索滑动面得到安全系数,讨论了加筋土筋带间距、筋带长度和筋-土界面的摩擦系数等因素的影响,对加筋土抗滑桩挡墙的支挡结构方案进行了优化;何思明等[8]对预应力锚索抗滑挡墙的结构特点、设计方法进行了研究,并与抗滑桩方案进行了对比;郑俊杰等[9]基于现场试验对某高速高填方桩基挡墙建立数值模型,提出桩基挡墙极限状态的确定方法,分析了填土重度、内摩擦角和桩间距等对结构稳定的影响;刘焕存等[10]对北京某顺层岩质滑坡设置挡墙组合结构,并对方案进行比选.综上所述,前人对桩—墙各类型式的组合结构进行了很多理论和实验上的研究,并取得了许多值得参考的经验,但是对于工程中应用较为广泛的抗滑挡墙结构缺少系统的研究.鉴于此,本文在根据工程经验的基础上建立三维抗滑挡墙边坡数值模型,就设桩参数变化对边坡稳定性的影响进行研究.
强度折减法[11]是ABAQUS数值软件在边坡稳定性分析中运用的理论基础,该法通过将坡体的黏聚力c和内摩擦角φ同时除以一个折减系数FS,得到一组新的ct、φt值后作为新的材料参数输入,再次进行试算,当体系内的最大不平衡力与内力的比值R小于10-5时计算中止,边坡达到极限平衡状态,此时对应的Fs即为边坡的安全系数,文中以坡脚位移曲线拐点对应的Fs为边坡安全系数.
本文通过把模型计算结果输出绘制成图,分析边坡的塑性区分布、最大塑性应变、边坡整体位移、挡墙顶部至底部的位移曲线、桩身的水平位移及边坡安全系数六大方面的数据,对抗滑挡墙结构的参数选用进行了优化设计.
1 建立计算模型
首先建立仅有挡墙作用时的边坡模型.使用ABAQUS数值模拟软件建立分析模型.图1为边坡计算模型,边坡和挡墙模型宽2 m,边坡底面长30 m,地基土高10 m;上部滑体为碎石土,高10 m,顶部长14 m,模型上部为某高速公路;挡土墙模型尺寸为上底面长3 m,下底面长6 m,高度为9 m的直角梯形;钢轨桩长10 m.因为是概化的模型,故输出的结果数值仅用做比较,具体计算参数见表1.
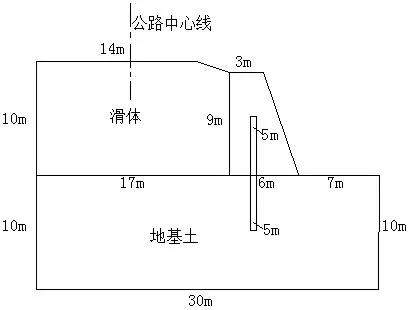
图1 边坡计算模型

表1 计算参数
模型中材料采用Mohr-Coulomb模型模拟,桩与挡墙采用线弹性理论模型模拟.挡墙与滑体之间的切向摩擦系数为0.55,法向接触采用“硬接触”.边界条件:对边坡挡墙侧面以y方向的约束,对边坡挡墙的前后侧以x方向的约束,对边坡底部以三个方向的约束,并对模型整体施加向下的重力.边坡模型以C3D8四面体为单元网格形状,进行结构化划分,划分后的模型如图2所示.首先对边坡模型进行地应力平衡,再进行强度折减的运算.
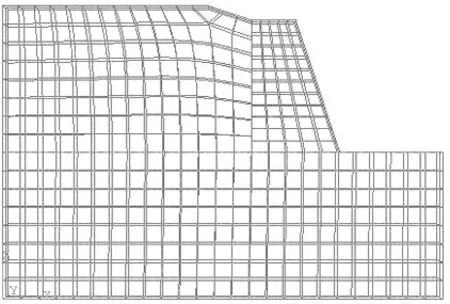
图2 边坡模型
图3中不难看出在没有布桩的情况下,塑性区是贯通的.图4是挡墙水平位移随挡墙高度的变化曲线.由图中的挡墙位移随高度的变化曲线得到挡墙顶部位移超过7.1 mm,挡墙底部位移为6.2 mm,且曲线呈现线性特征,经分析得无桩时边坡的安全系数0.69,边坡处不稳定状态.
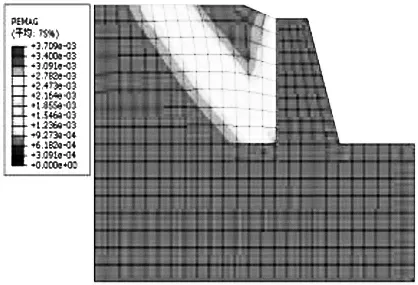
图3 边坡塑性区
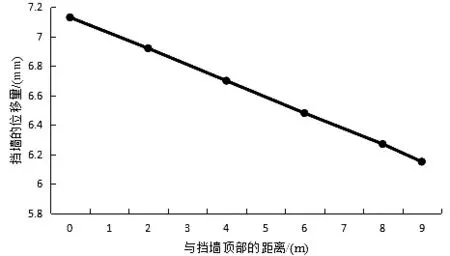
图4 无桩时的挡墙随其高度的位移量
1.1 设桩位置α变化对边坡稳定的影响
设桩位置的不同会对边坡稳定性产生影响,在此小节中,桩径均为0.5 m,桩在挡墙和地基土内长度均为5 m.设置三组桩位参数,分别建立桩距挡墙直角边底部3 m、2 m和1 m时的模型,如下图5(a)-5(c)所示,边坡整体的位移图如图6(a)-6(c)所示,塑性区分布图如下图7(a)-7(c)所示,桩的水平位移图如下图8(a)-8(c)所示,从挡墙顶部到底部的位移曲线图如图9,安全系数折线图如图10所示,在边坡上选取与挡墙上部接触位置为分析点,挡墙选取其左上部点为分析点,以下同上.在ABAQUS中对数据提取,并罗列在表2中.
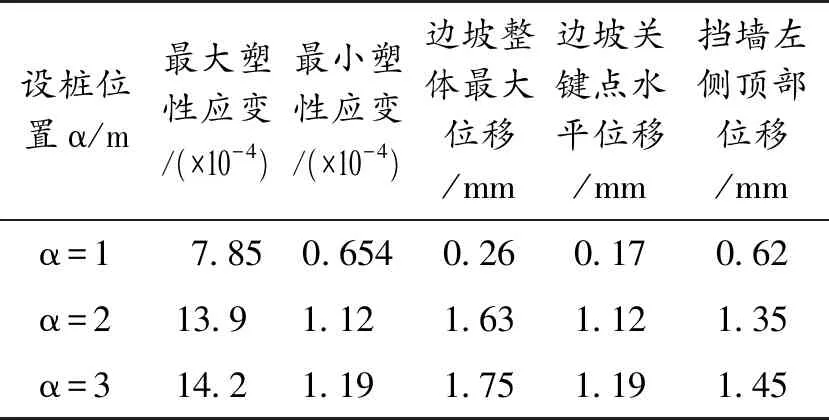
表2 设桩位置α不同时关键数据对比表
从云图和表2中可以看出,当有抗滑桩布设时,相关位移明显减小.图7(a)中的塑性区相比仅挡墙作用下没有贯通,最大塑性应变为1.42×10-3, 远小于无桩时的最大塑性应变3.7×10-3,这是因为抗滑挡墙结构的共同作用提供了更大的抗滑力.图6(a)中边坡整体位移为1.75 mm,图8(a)中桩的上部发生了水平方向上1.04 mm的位移量,这些位移是上部滑体的作用体现.
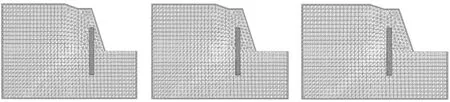
(a)α=3m (b)α=2 m (c)α=1 m

(a)α=3 m (b)α=2 m (c)α=1 m

(a)α=3 m (b)α=2 m (c)α=1 m

(a)α=3 m (b)α=2 m (c)α=1 m

图9 设桩位置α不同时抗滑挡墙结构体系的挡墙水平位移随高度关系曲线图
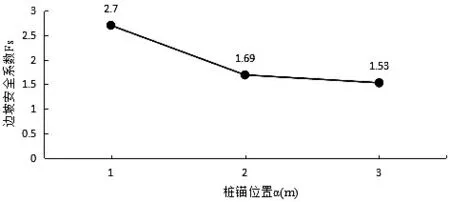
图10 设桩位置与边坡安全系数之间的关系
当设桩位置α=2 m时,从上图7(b)塑性区分布结果中可以看到,塑性区同样没有贯通,此时的最大塑性应变为1.39×10-3,略小于在α=3 m时的1.42×10-3,初步判断此处加固效果优于α=3 m.进一步分析,α=2 m中边坡的最大位移为1.63 mm,小于α=3 m中边坡的最大位移,α=2 m桩的水平位移为0.974 mm,也小于α=3 m时1.04 mm的位移,也可说明上述判断是正确的.
当设桩位置在最左侧,也就是距离挡墙直角边α=1 m位置时,从边坡位移图6(c)上看,最大位移基本分布在贴近挡墙左侧的地方,数值大小为0.26 mm,不仅远小于α=2 m的位移,也小于α=3 m时的位移,初步推测此处因桩距离滑动土体最近,与挡墙结合具备更好的抗滑能力.从塑性分布图7(c)中可以明显看出此时的塑性区相比α=2 m,α=3 m时有更小的范围,最大塑性应变为7.85×10-4,同样远小于以上两种情况.图8(c)桩在水平方向的位移图可知最大水平位移为0.132 mm,也远小于α=2 m,α=3 m的情况.
当设桩位置α在距挡墙直角边3 m、2 m和1 m时,边坡中选取的分析点在x方向位移分别为1.19 mm、1.12 mm和0.17 mm.
为了更明显地看出挡墙的位移,下面将上述三种设桩位置下的挡墙位移曲线图绘制出来.
图9中的三条线段分别代表的是设桩位置分别为α=1 m,α=2 m,α=3 m三种情况下挡墙随高度的位移变化,其数值大小在很大程度上能反映出边坡的稳定性.图中可以看到,α=3 m时的挡墙位移量最大,最大位移超过1.4 mm,最小位移也大于α=2 m时的最小位移,结合上述边坡位移和桩的水平位移可以说明当抗滑桩布设在此位置时边坡整体的稳定性最差.设桩位置在α=2 m时的挡墙水平位移是小于α=3 m情况下的,结合上述两类位移,可以验证初步结论推断的正确性,设桩位置α= 1 m时,挡墙的位移曲线显示的位移量最小,结合上面两组位移,可以得出在α=1 m位置布桩时边坡稳定性最好.
设桩位置与边坡安全系数的关系如图10所示:①设桩位置逐渐靠近挡墙直角边下底面时,边坡的安全系数呈现逐步增大的趋势.②设桩位置在3 m和2 m之间布设对边坡的安全系数影响不大,当设桩位置在2 m和1 m之间时,边坡安全系数明显增大,设桩位置在1 m处时边坡的安全性最高.
1.2 桩径大小对边坡稳定的影响
桩径b的大小也会对边坡的稳定产生影响,半径越大意味着桩材的用料和桩的成本越大.为研究桩径大小对边坡稳定的影响,分别建立了三组数值模型,第一组桩径为0.5 m,第二组桩径为0.4 m,第三组桩径为0.3 m,三组模型里设桩位置α=3 m并且挡墙和地基内桩长均为5 m,其他参数不变.分别在ABAQUS软件中输出边坡的整体位移图(图11(a)-11(c))、桩的水平位移图(图12(a)-12(c))和边坡塑性应变图(图13(a)-13(c)),表3为关键数据对比表.

表3 桩径b不同时关键数据对比表
由云图和表3可以看出,图11(a)中当桩径b=0.5 m时边坡整体最大位移为1.75 mm,图11(b)中当桩径b=0.4 m时边坡整体最大位移是1.78 mm,图11(c)当桩径b=0.3 m时边坡整体最大位移量是1.95 mm,即随着桩径的减小,边坡整体位移是增大的;与图12中桩的水平位移同样一致,图12(a)中当桩径b=0.5 m时桩的最大水平位移为0.97 mm,图12(b)中当桩径b=0.4 m时桩的最大水平位移为1.08 mm,图12(c)中当桩径b=0.3 m时桩的最大水平位移为1.25 mm,即桩的水平位移随桩径b的减小也是逐渐增大的.图13(a)-13(c)分别为桩径b不同时边坡的塑性区分布,从塑性图中看,b=0.3 m时的塑性区较为贯通,结合以上分析,也可得出此时边坡的稳定性最差.

(a)b=0.5 m (b)b=0.4 m (c)b=0.3 m
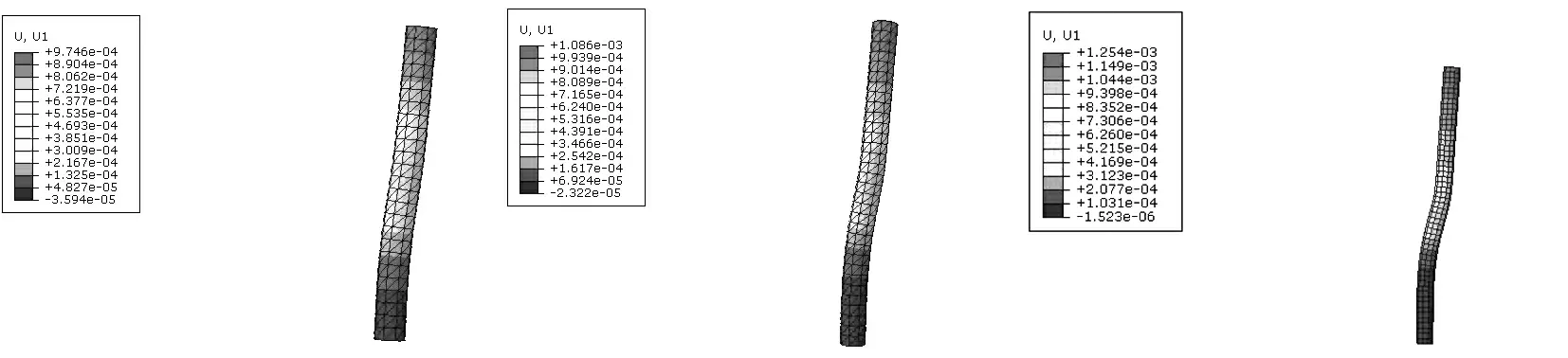
(a)b=0.5 m (b)b=0.4 m (c)b=0.3 m

(a)b=0.5 m (b)b=0.4 m (c)b=0.3 m
对边坡中的关键点进行位移分析,当桩径b=0.5 m、0.4 m和0.3 m时,位移大小分别为1.19 mm、1.21 mm和1.37 mm.
为了更加清楚地分析桩径b的变化对边坡稳定影响程度的大小,通过ABAQUS软件导出了挡墙随高度变化的位移曲线,如下图14所示.
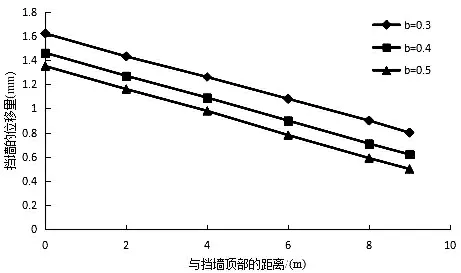
图14 桩径b不同时抗滑挡墙结构体系的挡墙水平位移随高度关系曲线图
从挡墙位移曲线图中可看出,当桩径b=0.5 m时,挡墙的位移在0.5 mm~1.35 mm间;当桩径b=0.4 m时,挡墙的位移在0.6 mm~1.45 mm间;当桩径b=0.3 m时,挡墙位移增大许多,在0.8 mm~1.62 mm间,即桩径b越小,挡墙位移越大,和图9中设桩位置α不同所引起的挡墙位移变化比要小些,说明边坡的稳定实际上受设桩位置α的影响更多.所以工程中如采用类似的抗滑挡墙加固边坡时,可在控制造价和节省桩材的情况下,尽可能使桩布设在靠近梯形挡墙直角的位置.
桩径b与边坡安全系数关系如图15所示:①边坡的安全系数随着桩径b的增大而增大.②桩径b由0.4 m到0.5 m之间安全系数相差不大,在控制钢材用料和造价的前提下,可优先选用0.4 m桩径的钢轨桩.
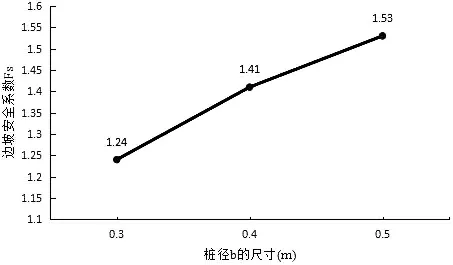
图15 桩径b与边坡安全系数的关系
1.3 挡墙内桩长对边坡稳定的影响
此小节主要讨论挡墙内桩长变化对边坡稳定的影响,通常挡墙内桩长不同会影响边坡稳定,而对于抗滑挡墙结构的研究总体是偏少的,对桩在挡墙和地基土内锚固深度这一因素的思考和研究更为少见.为此建立了两组模型,两组模型中桩的长度均为10 m,设桩位置α在距挡墙直角底边2 m处,桩径取0.5 m,其他参数保持不变.第一组模型中挡墙内桩长为3 m,地基土内桩长为7 m;第二组模型中挡墙内桩长为7 m,地基土内桩长为3 m.并在ABAQUS软件中对计算结果进行输出,如图16(a)-16(d)、17(a)-17(d)中所示.边坡模型运算后,分别得到挡墙内不同桩长时边坡坡内的塑性应变、边坡的变形位移以及挡墙的变形位移情况,并将数据整理列于表4中.
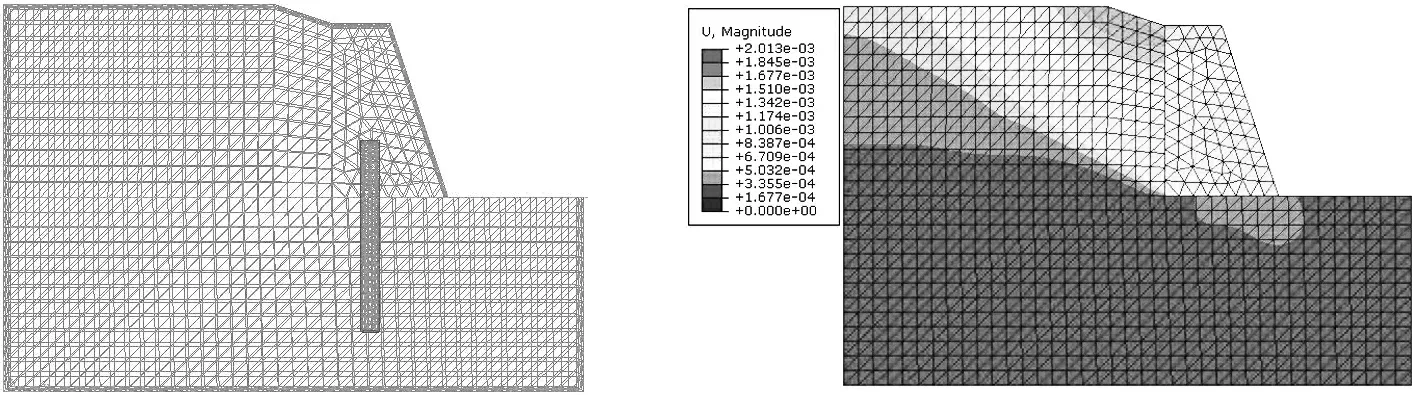
(a)模型 (b)边坡位移
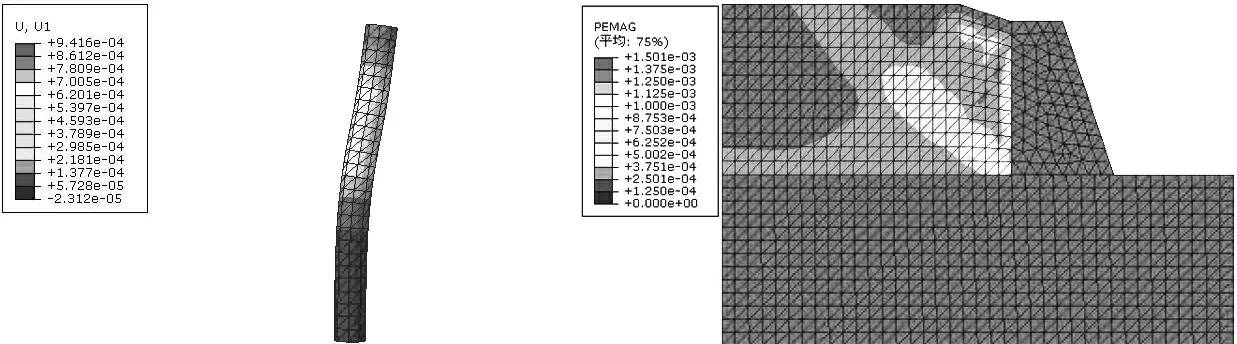
(c)桩x位移 (d)塑性区
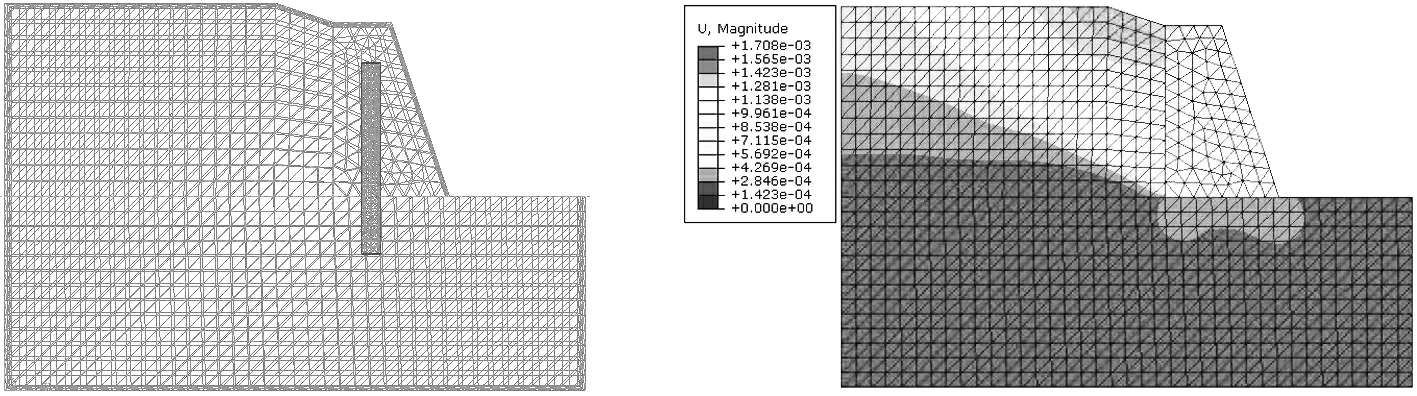
(a)模型 (b) 边坡位移

(c)桩x位移 (d)塑性区

表4 挡墙内桩长h不同时关键数据对比表
从云图和表4中可看出,挡墙内桩长h=3 m和h=7 m时边坡的最大位移均产生在滑体上部且靠近挡墙,h=3 m时边坡内最大位移为2 mm,大于h=7 m时边坡内的最大位移1.7 mm.从桩的位移图上看到,h=3 m和h=7 m时桩的最大水平位移均发生在顶部,h=3 m时大小为0.94 mm,后者大小为1.2 mm.从桩受力上看,挡墙内桩长h=7 m较h=3 m更长,受到更多的水平推力,产生更大的水平位移.挡墙内桩长h=3 m时和h=7 m时的塑性区较为接近,挡墙内桩长h=5 m时边坡整体最大位移为1.63 mm,与h=7 m时接近.
由表4知,当挡墙内桩长h=3 m、5 m和7 m时,边坡关键点的水平位移分别为1.37 mm、1.12 mm和1.16 mm,故h=3 m时边坡稳定性最差,h=5 m与h=7 m时边坡稳定性最好.
图18为三种情况下,挡墙随高度变化的水平位移图.挡墙内桩长h=3 m时,挡墙最大位移为1.65 mm,挡墙内桩长h=7 m时,挡墙最大位移为1.42 mm,大小和挡墙内桩长h=5 m时位移较为接近.所以,当挡墙内桩长大于地基土时,对挡墙位移影响不大.
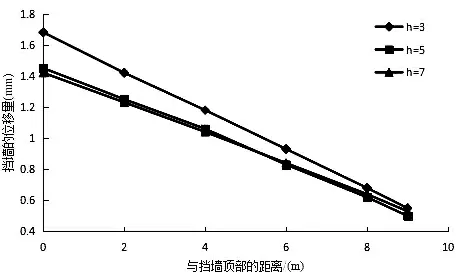
图18 h=3 m、5 m和7 m时挡墙随高度的水平位移图
挡墙内桩长h与边坡安全系数的关系如图19所示:①随着挡墙内桩长的增大,边坡的安全系数也随之增大.②在挡墙内桩深h=3 m至5 m时,边坡安全系数增加明显,当h=5 m至7 m时,边坡安全系数变化较小.
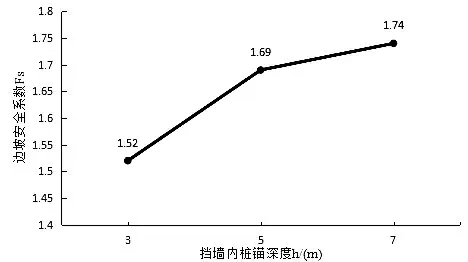
图19 挡墙内桩长h与安全系数的关系
1.4 桩身混凝土标号对边坡稳定性的影响
为研究钢轨桩与混凝土桩对边坡的稳定性影响,分别设置了C25、C30、C40和C50四种不同标号的混凝土桩,桩径b=0.4 m,挡墙和地基中桩深均为5 m,设桩位置α在距挡墙直角底边3 m处.通过查阅参数,并转化成ABAQUS通用单位,如表5所示.
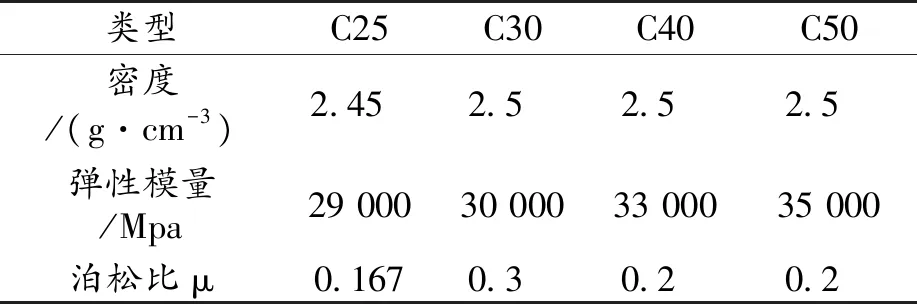
表5 桩身混凝土标号计算参数
不同桩身混凝土标号下的抗滑挡墙结构的边坡塑性区如图20(a)-20(d), 边坡整体位移如图21(a)-21(d),桩在水平方向上的位移图如图22(a)-22(d),挡墙顶部到底部的位移曲线如图23.

(a)C25塑性区 (b)C30塑性区
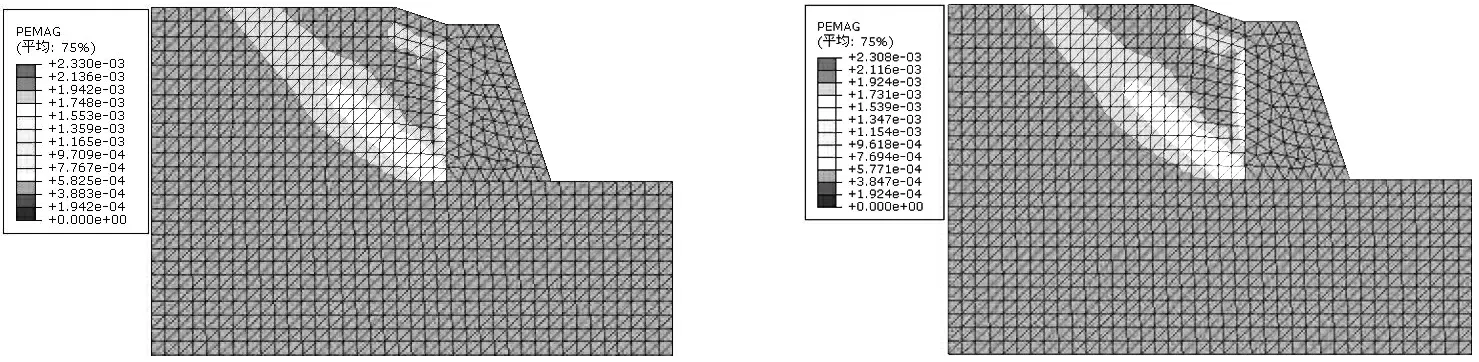
(c)C40塑性区 (d)C50塑性区
将运算后得到的坡内塑性应变值,边坡的变形位移和挡墙的变形位移量,分别整理后列在表6中.表6中可得如下信息:①当桩身混凝土标号为C25时,最大塑性应变为2.38×10-3,桩身标号C30时值为2.35×10-3,桩身标号C40时值为2.33×10-3,桩身标号C50时值为2.30×10-3,随着桩身混凝土标号的提高,边坡的最大塑性应变逐渐降低;②边坡的最大整体位移分别为2.21 mm、2.19 mm、2.18 mm和2.17 mm,同样呈现下降趋势;③桩的水平位移也随桩身混凝土标号的增大而减少.

(a)C25位移图 (b)C30位移图

(c)C40位移图 (d)C50位移图

(a)C25桩x位移图 (b)C30桩x位移
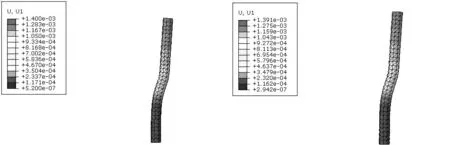
(c)C40桩x位移 (d)C50桩x位移
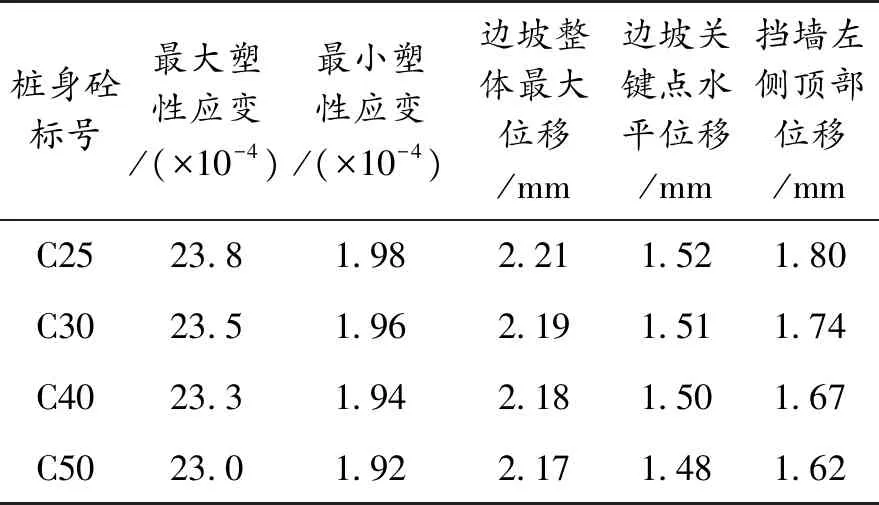
表6 不同桩身混凝土标号时关键数据对比表
对边坡中关键点进行位移分析,当桩身混凝土标号为C25~C50时,点位的位移分别为1.52 mm、1.51 mm、1.50 mm和1.48 mm.
图23为不同桩身混凝土标号下桩对挡墙水平位移的影响.桩身混凝土标号越高,挡墙的水平位移越小.同时,不同桩身混凝土标号对边坡的整体影响有限.
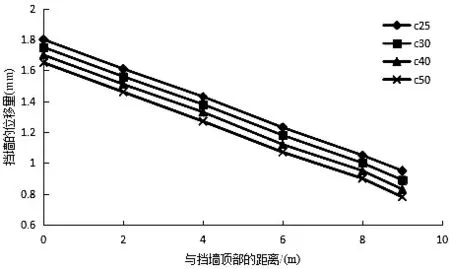
图23 不同桩身混凝土标号下挡墙从顶部到底部的位移曲线
图24为不同桩身混凝土标号与边坡安全系数的关系,可看出边坡的安全性逐步增加,同时安全系数较为接近.
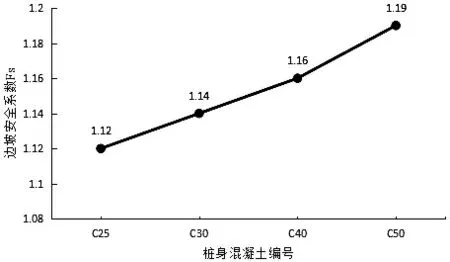
图24 不同桩身混凝土标号与边坡安全系数关系
2 结论
通过控制变量的方法,对建立的抗滑挡墙边坡模型进行数值模拟,可以得出如下结论:
(1)在抗滑桩与挡墙的共同作用下,其中抗滑桩发挥更大的作用,大大减小边坡失稳和破坏的可能性,边坡安全系数显著增加.
(2)抗滑挡墙中桩径b的改变对边坡的稳定性有显著影响,桩径b越大,边坡的变形和位移越小,边坡的安全性也越高.在模型中边坡与挡墙宽2 m,桩径b为0.4 m时可在最大限度节省造价的前提下使边坡获得较好的稳定性.
(3)当抗滑桩的加固位置接近挡墙直角边时,挡墙和边坡塑性区会大大地减小,当设桩位置位于距挡墙直角下底面1/6~1/3处时,边坡的安全系数最高,稳定性最好.
(4)当挡墙内桩长越长,抗滑挡墙对边坡的抗滑效果也越好,当挡墙内桩长减小时,边坡的整体位移相应增大,安全系数减小.经研究,当挡墙内桩长在5 m~7 m,即1/2~7/10总桩长下,边坡的安全系数最高,稳定性最好.
(5)桩身混凝土标号越大,挡墙的位移越小,边坡的安全性越高,同时安全系数较为接近.通过比较发现,混凝土桩在抗滑挡墙结构中对边坡的抗滑效果不如钢轨桩.工程中可根据实际造价预算和对边坡稳定性的要求选用钢轨桩或混凝土桩,如采用混凝土桩,建议选用C25型.
