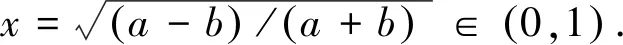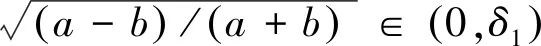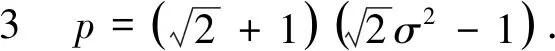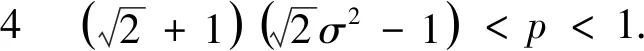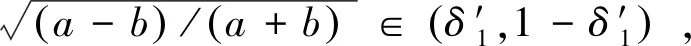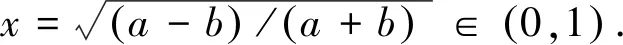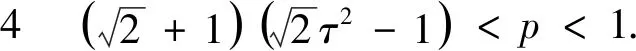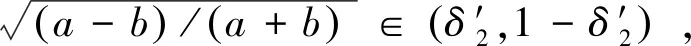双纽线平均的算术与二次平均调和组合界
2021-09-29李少云王君丽何晓红徐会作
李少云 王君丽 何晓红 徐会作
(1.温州广播电视大学 教师教学发展中心,浙江 温州 325000; 2.台州科技职业学院 成人教育学院,浙江 台州 318020; 3.衢州广播电视大学教务处,浙江 衢州 324000;4.温州理工学院 数学与信息工程学院,浙江 温州 325000)
0 前言
Gauss反双纽线正弦函数和反双纽线双曲正弦函数[1,2]分别定义如下:

另外一对反双纽线函数,即反双纽线正切和反双纽线双曲正切函数[3]定义为
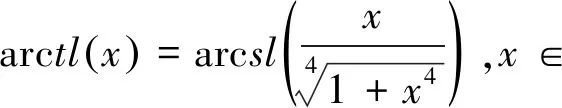
我们不难证明(见文献[2]定理1.7):
和
其中

是经典伽玛函数[4]以及
是第一类完全椭圆积分[5,6].
对于a,b>0且a≠b,算术平均A(a,b),二次平均Q(a,b)和双纽线平均LM(a,b)[3]分别定义如下:
(1)
和
上述四种反双纽线函数可以用R-超几何函数来表示[3].近年来,涉及反双纽线函数和双纽线平均的不等式引起了国内外学者的关注.在特殊情形,可以发现一些新的重要不等式,相应结果可参见有关文献[7-14].
设a,b>0且a≠b,z=|a-b|/(a+b)∈(0,1),LMAQ(a,b)=LM[A(a,b),Q(a,b)],LMQA(a,b)=LM[Q(a,b),A(a,b)].则这两个平均LMAQ(a,b)和LMQA(a,b)的显式表达式为:
(2)
(3)
Neuman[3]证明了不等式
A(a,b) (4) 对所有a,b>0且a≠b成立. 根据不等式(4),本文的主要结论是如下两个定理: 定理1双向不等式 定理2双向不等式 定理1和定理2揭示了双纽线平均和算术平均与二次平均调和组合的序关系,进一步可以分别获得反双纽线双曲正弦函数和反双纽线正切函数的估计. 为了证明定理1和定理2,本节给出反双纽线函数的求导公式和两个引理. 首先,根据反双纽线函数的定义和复合函数求导法则,容易得到如下求导公式: . 下面,我们给出本文需要的两个引理. 引理1.1设p∈(0,1), f(t)=3pt4+3pt3-(1-p)t2-4(1-p)t-4(1-p) (5) 证明(1)当p=3/5时,则等式(5)变成 (6) 7p-1=2.6397…>0,13p-4=2.7594…>0, f(1)=3(5p-3)=-1.2006…<0, (7) (8) f′(t)=12pt4+9pt2-2(1-p)t-4(1-p)>12pt+9p-2(1-p)t-4(1-p) =2(7p-1)t+(13p-4)>0 (9) 引理1.2设p∈(0,1), g(t)=4pt4+4pt3+pt2-3(1-p)t-3(1-p) (10) 证明(1)当p=2/5时,则等式(10)变成 (11) 11p-1=2.5662…>0,g(1)=15p-6=-1.1369…<0, (12) (13) g′(t)=16pt3+12pt2+2pt-3(1-p)>3(11p-1)>0 (14) 定理1 1/LMAQ(a,b)-[p/A(a,b)+(1-p)/Q(a,b)] (15) 设 (16) 则简单计算可得 F(0+)=0, (17) (18) (19) 其中 (20) (21) 其中f(t)是定义在引理1.1. 下面分四种情形证明: 情形1p=3/5.由式(15)-(17),(19)-(21)和引理1.1得到 情形2 0 (22) F(1-)=0. (23) 由式(15)-(17)、(23)及函数F(x)的分段单调性,可知 F(1-)<0. (24) 定理2 1/LMQA(a,b)-[p/A(a,b)+(1-p)/Q(a,b)] (25) 设 (26) 则简单计算可得 G(0+)=0, (27) (28) (29) 其中 (30) (31) 其中g(t)是定义在引理1.2. 下面分四种情形证明: 情形1p=2/5.由式(25)-(27),(29)-(31)和引理1.2得到 情形2 0 (32) G(1-)=0, (33) 由式(25)-(27)、(33)及函数G(x)的分段单调性可知 G(1-)<0. (34) 由定理1和定理2,我们得到如下推论: 推论双向不等式 对所有x∈(0,1)成立.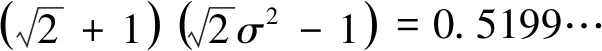
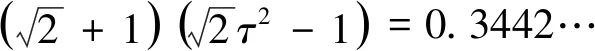
1 引理
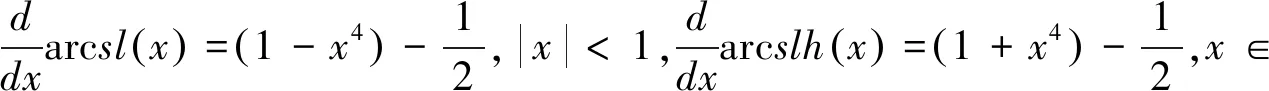
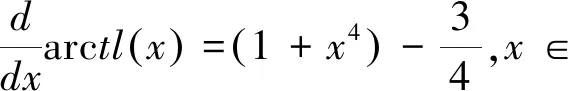

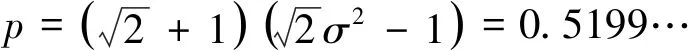

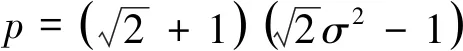


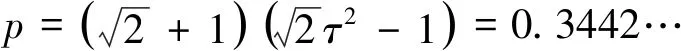


2 定理证明