基于广义岭估计的结构模型修正方法
2021-09-29杨秋伟李翠红
杨秋伟 陈 华 李翠红
(1.绍兴文理学院 土木工程学院,浙江 绍兴 312000; 2.宁波工程学院 建筑与交通工程学院,浙江 宁波 315211;3.浙江省土木工程工业化建造工程技术研究中心(宁波工程学院),浙江 宁波 315211)
0 引言
有限单元法已广泛用于土木、机械、航空航天、汽车、船舶等众多工程设计领域中,已经成为解决复杂工程分析计算问题的有效途径.利用实际工程结构的有限元模型,可开展力学计算、响应预测、优化设计和损伤识别等研究.因此,一个准确的有限元模型是上述工作能够成功开展的基础.然而,由于工程结构的复杂性,用有限元软件所建立的结构模型与真实结构总是存在着一定的差异,具体体现在:由有限元模型计算所得的结构响应参数(如位移、频率和振型)总是与仪器测试所得的结构响应参数存在着差异.当这种差异较大时,则必须对结构的有限元模型进行修正,即通过修改模型中部分单元的物理参数,来使得计算所得的响应参数与测试所得的响应参数尽可能接近,修正后的有限元模型方可用于力学分析与计算中,这种方法称为模型修正法[1-7].
数据误差是困扰模型修正法成功实施的一个关键问题.一方面,由于测试设备和条件的限制,以及环境因素(如温度、湿度、偶然荷载)的干扰,测试所得的结构响应参数必然存在着或大或小的误差;另一方面,结构建模时所采用的物理参数如弹性模量等的理论值和实际值也总是存在一定的偏差,当采用这些含有误差的数据进行模型修正计算时,往往会出现病态最小二乘问题[8-10].为了解决病态最小二乘问题,许多学者开展了岭估计和广义岭估计方面的研究[11-23],这类方法的主要难点在于岭参数的选择,常见的L曲线法或岭迹法均需要很大的计算量且所得结果精度有限.有鉴于此,本文提出一种新的广义岭估计方法,所提方法充分考虑系数矩阵对角元素之间的差异,提出一个底数可调节的正则系数计算公式,用于获得广义岭估计中的正则对角矩阵,可以尽量减少广义岭估计中由于引入正则矩阵而带来的额外误差,更好地兼顾解的稳定性和准确性,计算快捷且精度高.以一个病态方程组和一个桁架结构为例验证了所提方法,结果表明,所提方法能有效克服数据噪声的不利影响,改善方程组的病态性,获得比现有方法精度更高的计算结果.
1 模型修正方程组
结构模型修正可以利用静力测试数据或动力测试数据来进行,不失一般性,本文利用静力位移来建立结构模型修正方程组,简述如下:
设结构初始有限元模型的刚度矩阵为K,在已知的外载荷l的作用下,结构将产生静力位移.由初始有限元模型可以计算得到位移的数值解u0为[7]:
u0=K-1l
(1)
另一方面,通过实际静力测试,可以获得结构在外载荷l作用下的位移实验值ue,由于建模误差以及测量误差,u0和ue总是存在偏差,需要修正刚度矩阵K以使得计算所得位移值与测试所得位移值更接近.设有限元模型中各单元的修正系数为ci,则修正后的刚度矩阵Km可表示为[7]
(2)
其中Ki为有限元模型中第i个单元刚度矩阵,N为单元的总数目.理论上,由修正后的刚度矩阵Km计算所得的位移值应等于实测值ue,即
(3)
方程(2)代入(3),利用Neumann级数展开并忽略高阶项可得:
(4)
方程(1)代入(4)并整理可得:
A·x=y
(5)
A=[η1,…,ηN],ηi=K-1KiK-1
(6)
x=(c1,…,cN)T
(7)
y=ue-u0
(8)
上述方程中,系数矩阵A可以通过初始有限元模型由方程(6)计算获得,向量y可以由实验测试值及初始有限元模型由方程(8)计算得到,修正系数向量x为未知的向量,也是要求解的列向量.因此,模型修正问题最终可以归结为线性方程(5)的求解问题.最小二乘估计是求解线性方程组最常用的方法,它满足最优线性无偏性,因此又称为无偏估计.最小二乘估计主要计算公式[8,9]为:
首先,方程(5)两边乘以AT可得法方程为:
z=B·x
(9)
B=ATA
(10)
z=ATy
(11)
其中方阵B称为法方程的系数矩阵.由方程(9)可得x的最小二乘估计为:
xlse=B-1·z
(12)
然而,当系数矩阵B呈现病态或严重病态时,即矩阵B的条件数很大或矩阵B近似为奇异矩阵,此时,由方程(12)计算所得的最小二乘估计xlse将严重偏离x的真值,必须寻求x的更好估计.
2 一种新的广义岭估计方法
为了解决病态最小二乘问题,许多学者开展了岭估计和广义岭估计方面的研究.从矩阵方程的角度来看,岭估计的基本思想是:在系数矩阵B中增加一个正则对角矩阵kI,以降低系数矩阵的条件数,从而获得更加稳定估值,其计算公式为:
xre=(B+kI)-1·z
(13)
其中xre为x的岭估计,I为和系数矩阵B同维的单位矩阵,系数k称为岭参数.如果把方程(13)中的正则矩阵kI更换为一般的对角矩阵Λ,则可得广义岭估计xgre的计算公式为:
xgre=(B+Λ)-1·z
(14)
(15)
显然,对比方程(12)、(13)和(14)可知,当k1=k2=…=kn=k时,广义岭估计退化为岭估计,当k1=k2=…=kn=0时,岭估计退化为最小二乘估计.目前,岭估计方法的主要问题在于选择岭参数往往需要很大的计算量,且精度不高.为了进一步提高计算精度,并避免岭参数选择所需要的复杂运算,本文提出一种新的广义岭估计方法如下.
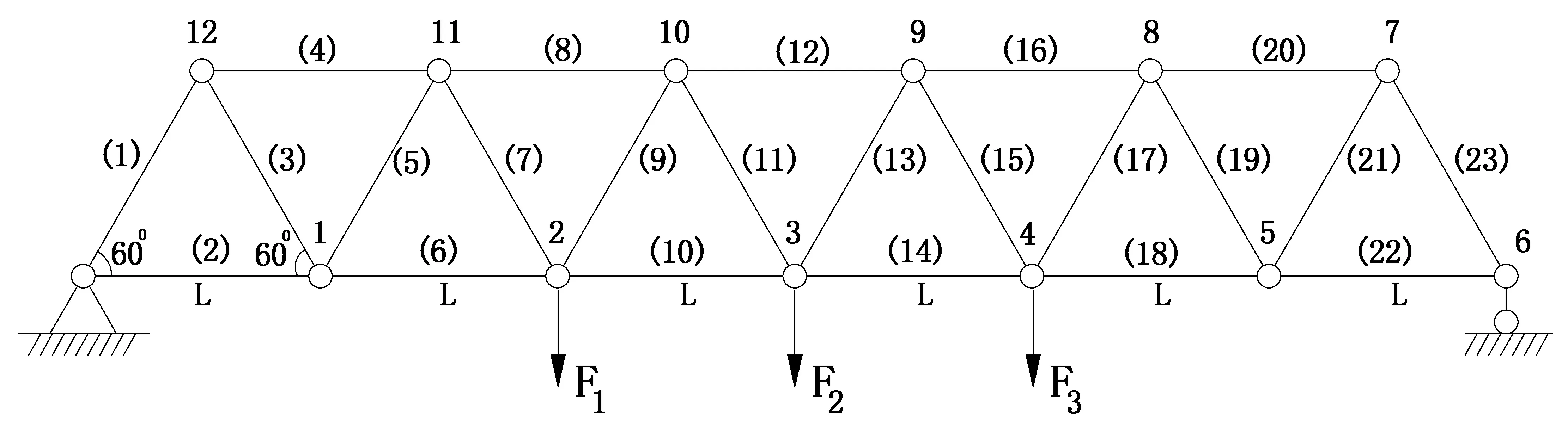
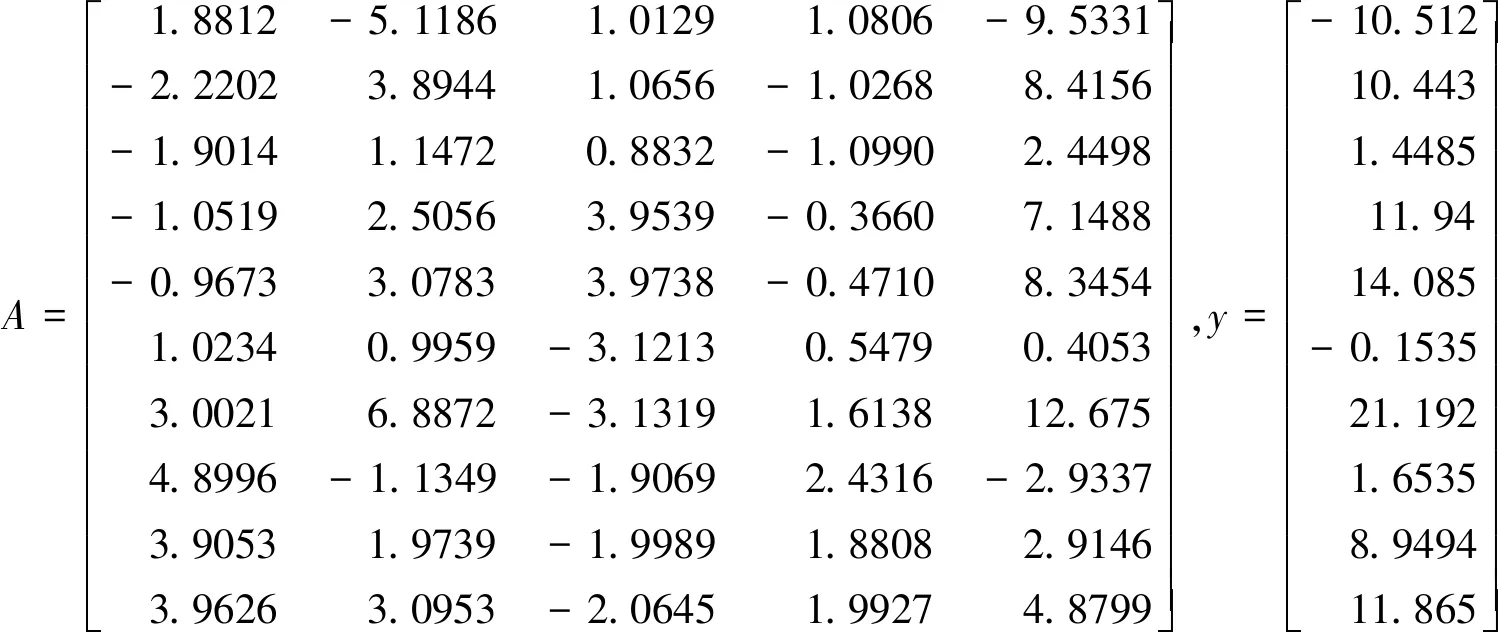
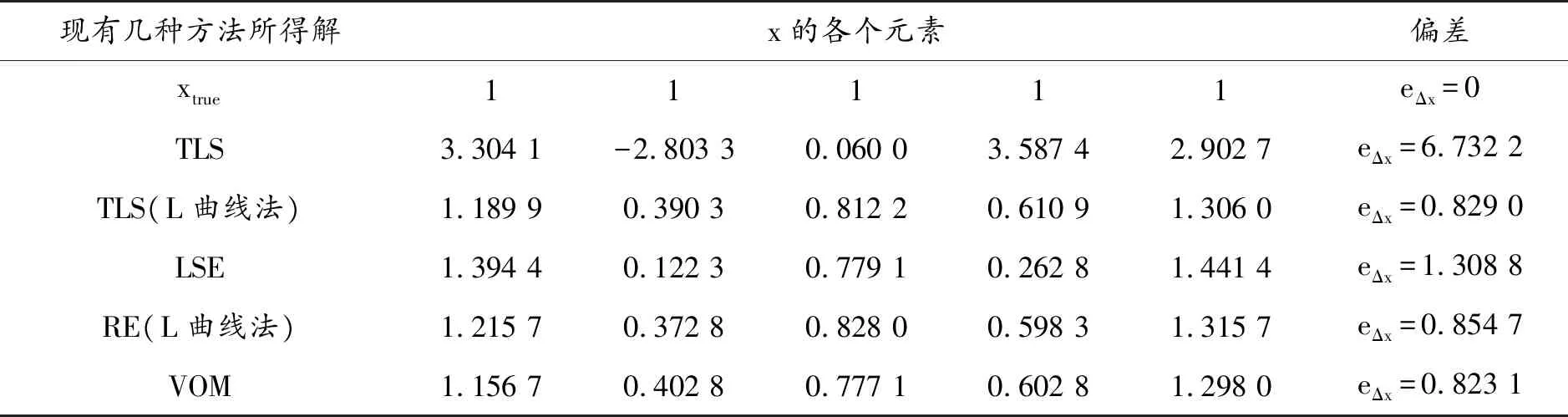
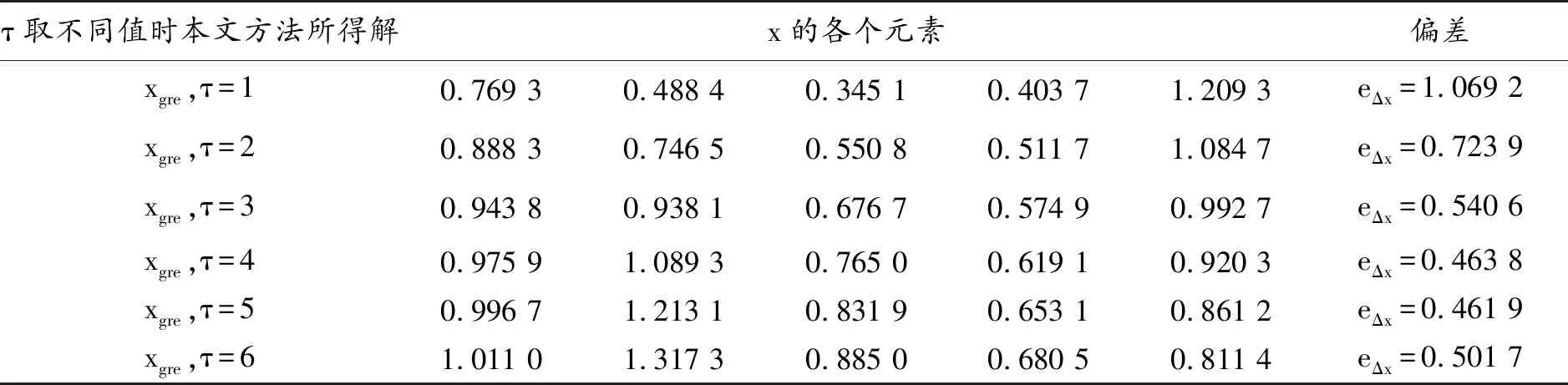
首先,分析广义岭估计的计算公式(14)可知,正则矩阵Λ的作用是两方面的:其正面作用在于,引入正则矩阵Λ可以降低系数矩阵的条件数,即cond(B+Λ) 设系数矩阵B中的元素为bij(i=1~n,j=1~n),即 (16) 找出方程(16)中B对角元素的最大值,记为bmax,即 bmax=max(bii),i=1~n (17) 则广义岭估计中正则矩阵Λ(方程(15))中对角元素由以下公式来计算: (18) 其中,τ是一个可以调节的底数,只需满足τ≥1即可.显然,如果τ取为1,则方程(18)退化为k1=k2=…=kn=0.05×bmax,相当于广义岭估计退化为常规的岭估计.实际应用时一般可以取τ为2~10之间的某个整数. 最后,将所提的广义岭估计新方法操作步骤总结如下:首先,由方程(17)找出系数矩阵B中最大的对角元素;然后,由方程(18)计算正则矩阵Λ各对角元素,得到正则矩阵Λ;最后,由方程(14)计算未知量x的新广义岭估计解xgre. 3.1算例1 首先,以文献[24]中所模拟的病态方程组为例,来验证所提的广义岭估计方法,并将计算结果与现有的岭估计方法及其他几种方法进行比较,以说明本文所提方法的可行性与优势.该病态方程组的系数矩阵和观测向量具体为: (19) 该模型法矩阵的条件数为2.0837×104,病态性严重.文献[24]中给出了各种方法的解算结果,如表1所示,其中TLS表示整体最小二乘法,LSE表示最小二乘法,RE表示岭估计方法,VOM表示虚拟观测解法.为了衡量表1中各种方法计算结果的精度,定义eΔx为x的计算值与真值之间的偏差,其计算公式如下: eΔx=‖xestimate-xtrue‖2 (20) 其中下标“2”表示向量的2-范数. 采用本文所提广义岭估计新方法,τ从1取到6时的计算结果如表2所示.由表2可见,τ=4或τ=5时计算结果精度都比较好,进一步对比表1和表2可知,采用本文所提广义岭估计方法,τ取2到6时各个解的精度均要好于表1中的现有方法,进一步说明了本文方法是合理可行的. 3.2算例2 接下来以图1所示的桁架结构模型为例,来验证所提方法在结构模型修正中的应用.该结构中杆件材料的弹性模量为E=200 GPa, 密度为 ρ=7.8×103kg/m3,各杆件长度均为L=1 m,杆件横截面面积A=1.759×10-4m2.静力荷载为F1=F2=F3=10 kN.不失一般性,假设各杆件修正系数ci的真值为c2=c7=0.2,c15=0.1,c10=c20=0.15, 表1 现有方法的解算结果(算例1) 表2 本文所提广义岭估计方法计算结果 其他杆件的修正系数均假设为0.在由有限元模型计算所得的位移差向量中添加随机噪声来模拟测量误差,模拟误差的公式为: Δu=Δu×(1+δ×unifrnd(-1,1)) (21) 其中δ表示误差水平,本例中取δ=0.1;unifrnd(-1,1)表示一个位于[-1,1]区间里的随机数.分别运用最小二乘法、岭估计法和本文所提广义岭估计新方法,求解模型修正线性方程(5),计算所得结果列于图2中. 由图2可见,和修正系数的真值(即假设值)相比,本文所提方法的计算结果与之最接近.另外,也可利用公式(20)来衡量各计算结果与真值之间的偏差,三种方法计算结果的偏差分别为:0.548 8,0.256 6和0.178 0,也说明了本文方法计算精度最好.因此,本文所提方法可以应用于结构模型修正问题中,能够一定程度上克服数据噪声的不利影响,改善方程组的病态性,提高求解精度. 针对病态最小二乘问题,本文提出一种新的广义岭估计方法,并将其应用于结构有限元模型修正问题中.所提方法充分考虑系数矩阵对角元素之间的差异,提出一个底数可调节的正则系数计算公式,用于获得广义岭估计中的正则对角矩阵,从而尽量减少广义岭估计中由于引入正则矩阵而带来的额外误差,更好地兼顾了解的稳定性和准确性. 以一个病态方程组和一个桁架结构为例验证了所提方法,结果表明,所提方法能有效克服数据噪声的不利影响,改善方程组的病态性,获得比现有方法精度更高的计算结果. 图1 桁架结构及其静力加载 图2 各种方法计算结果对比(算例2)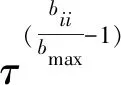
3 数值算例
4 结论