不可压热流体的离散统一气体动理学简化算法
2021-09-29蔡宏敏徐江荣梅鲁浩
蔡宏敏,徐江荣,梅鲁浩,王 路
(杭州电子科技大学能源研究所,浙江 杭州 310018)
0 引 言
流动与热交换广泛存在于自然界及工程领域,表现形式多种多样。从自然界中的大气循环、水循环、风霜雨雪的形成,到工业中微电子的散热冷却、航空航天飞行器的航行活动,都与流动和传热过程密切相关。传统的热流体力学研究从宏观角度出发,通过求解Navier-Stokes方程来研究热流动问题,逐渐发展成一套完善的解决热流过程问题的可靠方法[1-2]。但是,宏观方法难以克服连续性假设的制约,在稀薄流及微流动领域的局限性日益突出。以格子Boltzmann方法(Lattice Boltzmann Method,LBM)为代表的介观流体力学方法从分子底层分析流动与传热机理,为热流体的数值研究提供了新的思路[3-4]。传统的LBM在可压缩及稀薄流领域的研究也遇到难以突破的瓶颈,拓展一种广泛适用于连续流和稀薄流的统一数值方法仍是一个尚未彻底解决的科学问题。Guo等[5]提出的离散统一气体动理学方法(Discrete Unified Gas Kinetic Scheme,DUGKS)为发展跨越微观-宏观尺度的统一计算流体力学方法提供了新的可行性方案。DUGKS是一种基于有限体积的新方法,结合LBM和统一气体动理学(Gas Kinetic Scheme,GKS)方法的优点,成功应用于连续流和稀薄流的相关研究,并不断被发展完善[6]。Wang等[7]拓展了热流耦合的DUGKS方法,通过动力学边界条件分别独立求解流场内流体的速度和温度,成功模拟热流动现象。Yang等[8]使用DUGKS求解器,将相场方法应用于两相流的模拟中,有效地模拟了界面严重变形的几种情况,并且精准捕获了许多微妙的细节。Wu等[9]开发了一个守恒的DUGKS方法用于解决流场多尺度问题,在非结构化粒子速度空间中,宏观量由介观气体分布函数通量来更新,大大提高了效率。与LBM相比,DUGKS适用于任意努森数的流动,网格适用灵活,其数值精度和算法稳定性均有所提升[10-11],但在一个时间步长内需要演化多个分布函数,算法结构和计算效率需要进一步优化和提升。本文针对不可压缩热流体,通过优化演化过程中分布函数微通量的计算方法,提出一个简化的DUGKS,在不改变数值精度和稳定性的前提下,大幅提高了计算效率。
1 数值计算方法
本文采用双分布Boltzmann方程描述热流体的输运过程,碰撞项采用Bhatnagar-Gross-Krook(BGK)碰撞模型:
(1)
式中,fα为流体分布函数,当α=1,2时,fα分别表示流场分布函数和温度分布函数,ξ为流场内流体粒子速度,τα为松弛时间,feq为Maxwellian平衡态分布函数:
(2)
式中,R为气体常数,D为空间维度,ρ为宏观量密度,u为流体速度,T为温度。通过分布函数得到宏观量密度、速度以及温度:
(3)
方程(1)的求解采用类似于Richtmyer格式[12]的两步算法,网格节点分别采用实心与空心点表示,fn,fc分别为网格格点和网格中心点上的流体分布函数,其结构如图1所示。
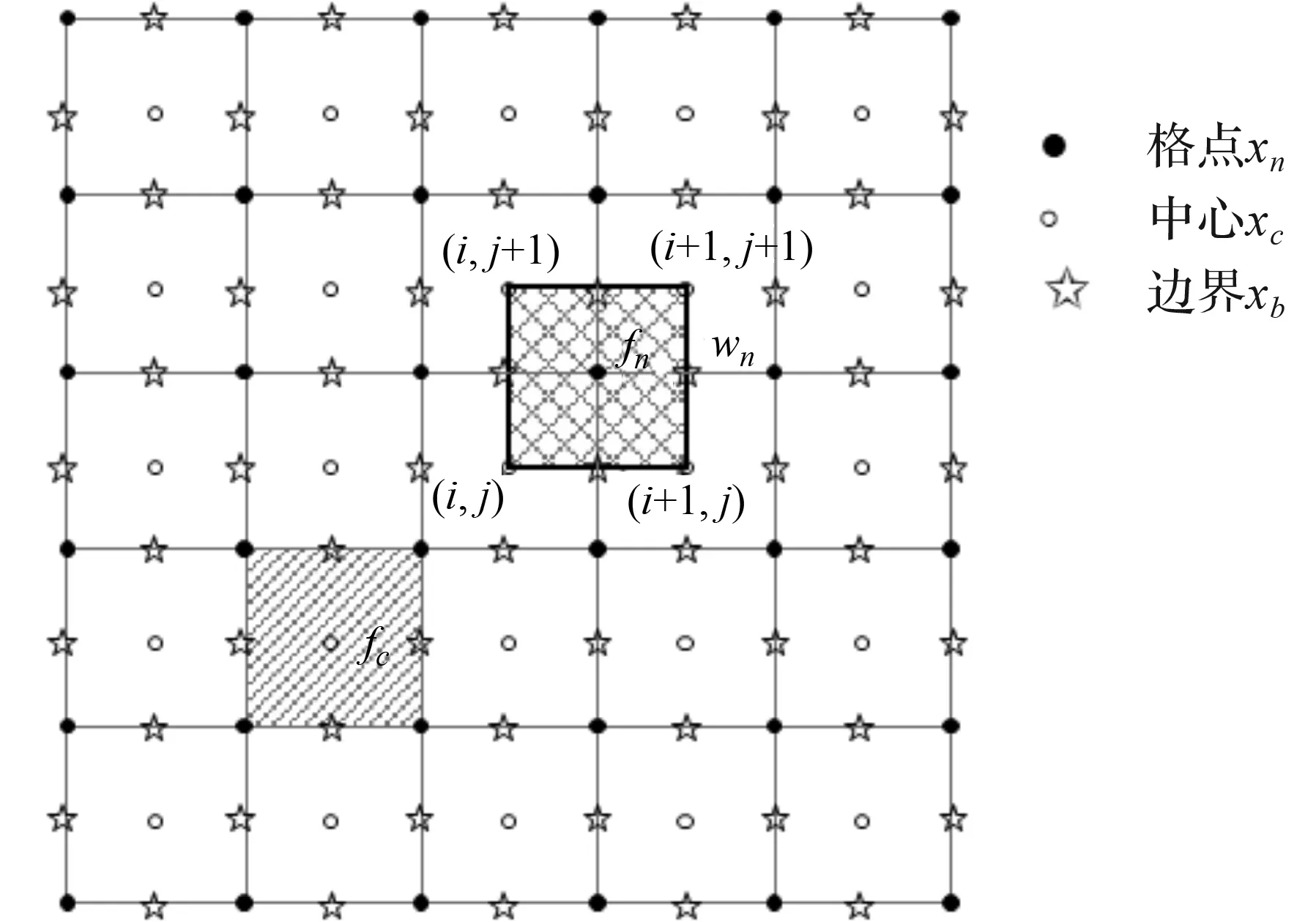
图1 二维网格示意图
首先,求解半个时间步长后格点xn处流体分布函数,碰撞项采用梯形法则,将方程(1)离散为:
(4)
其中,
(5)
(6)

(7)
(8)
进一步使用如下离散格式求得下一时刻的分布函数:
(9)
其中,
(10)
在热流问题的求解中,需要考虑传热与流动的耦合,根据Boussinesq假设,流体密度与温度呈线性关系:
ρ=ρ0-ρ0β(T-T0)
(11)
式中,ρ0,T0分别为流场中的平均密度和平均温度,β为热扩散系数,记重力加速度为g0。在Boussinesq假设下,重力与外力加速度表示为:
(12)
在演化过程中,外力项可以合并到碰撞项中,于是将流场分布函数控制方程中的碰撞项修正为:
(13)
碰撞项的修正不改变演化过程,算法将继续演化流场内分布函数,直至满足终止条件。
简化DUGKS算法的计算步骤如下:
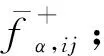
(7)重复步骤2—步骤6,直到达到终止条件;
(8)输出流场内的宏观物理量。
2 数值模拟结果与分析
2.1 仿真工况

图2 自然对流方腔示意图

2.2 仿真结果与分析
Ra分别为104,105,106时,采用本文算法以及DUGKS算法分别进行二维自然对流模拟,得到流场内温度分布情况分别如图3—图5所示。从图3—图5可以看出,随着Ra逐渐增大,温度场内的中部等温线由竖直逐步转变为水平,热端与冷端壁面附近的等温线逐渐密集,即等温壁面附近的温度梯度变化越发明显,方腔中部出现明显的温度分层现象。从图5可以看出,在等温壁面与绝热壁面的交汇处,温度呈现出先下降后升高的现象,从而导致等温线出现一个较大的波动。

图3 Ra=104下的方腔内温度场对比
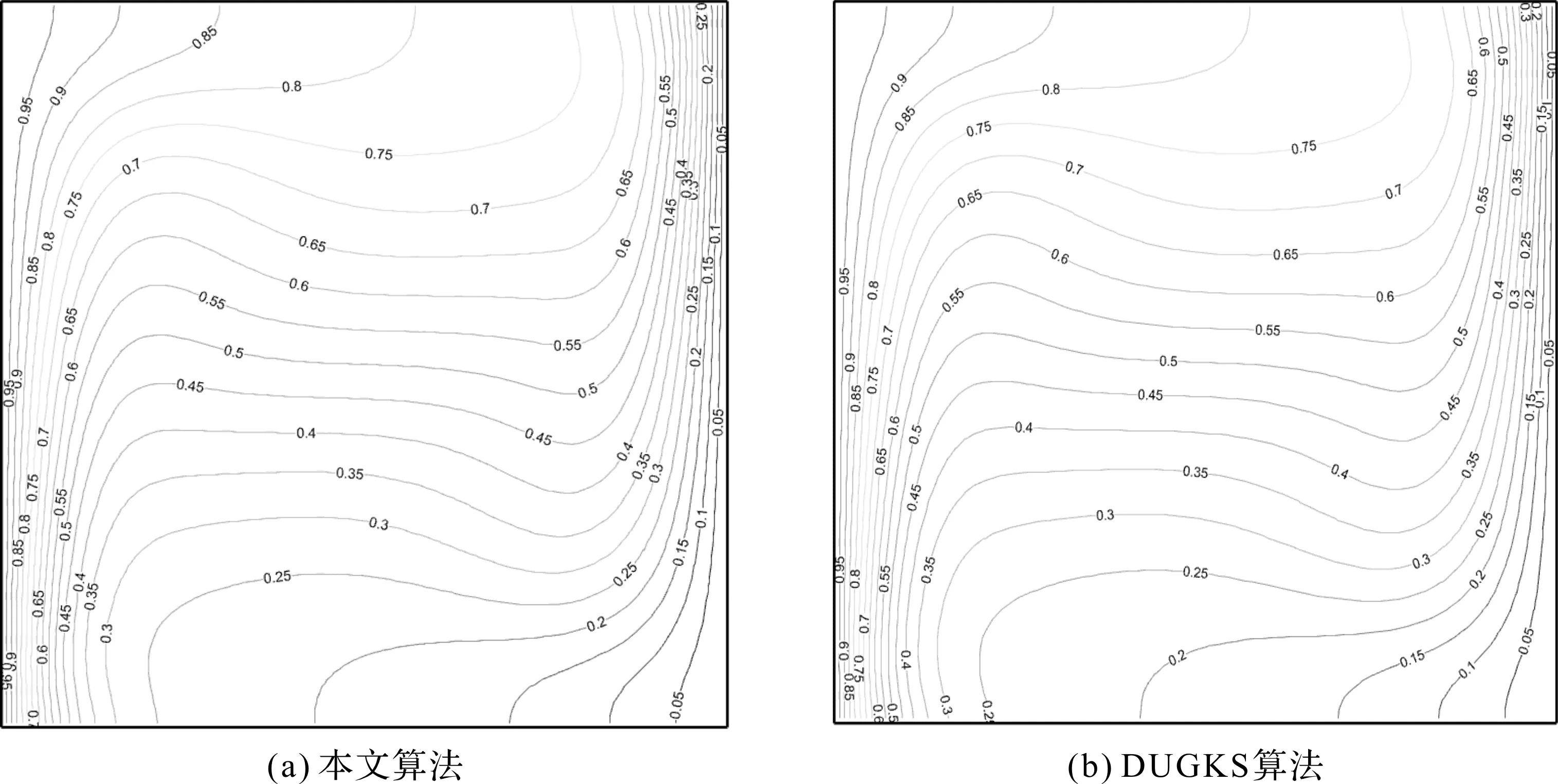
图4 Ra=105下的方腔内温度场对比

图5 Ra=106下的方腔内温度场对比
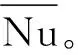

表1 不同Ra下,不同算法的模拟结果
在原始的DUGKS中,微通量的计算采用中心法则,需要对控制中心xc及边界中心xb处的流场及温度分布函数进行演化,一个时间步长的演化次数约为:
NDUGKS=imax×jmax+(imax+1)×jmax+imax×(jmax+1)≈3(imax×jmax)
(14)
本文采用梯形法则计算微通量,先后演化控制中心xc与格点xn不再需要计算边界中心处的流场及温度分布函数。一个时间步长的演化次数约为:
NSDUGKS=imax×jmax+(imax+1)×(jmax+1)≈2(imax×jmax)
(15)
理论上,本文算法的计算量相较于原始算法大约下降了1/3左右。
Ra=106时,分别采用本文算法、DUGKS算法进行二维自然对流模拟,得到方腔竖直中线处水平速度、方腔水平中线处的垂直速度以及温度分布如图6所示。从图6可以看出,在流场和温度场的模拟中,本文算法与DUGKS算法取得的结果非常吻合。
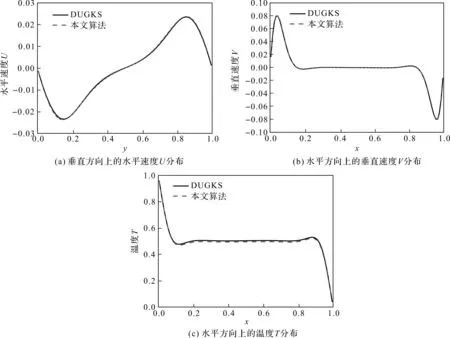
图6 水平中线处速度分布和温度分布比较
为了比较2种算法的演化速度,设置方腔内水平速度残差E为终止条件,
(16)
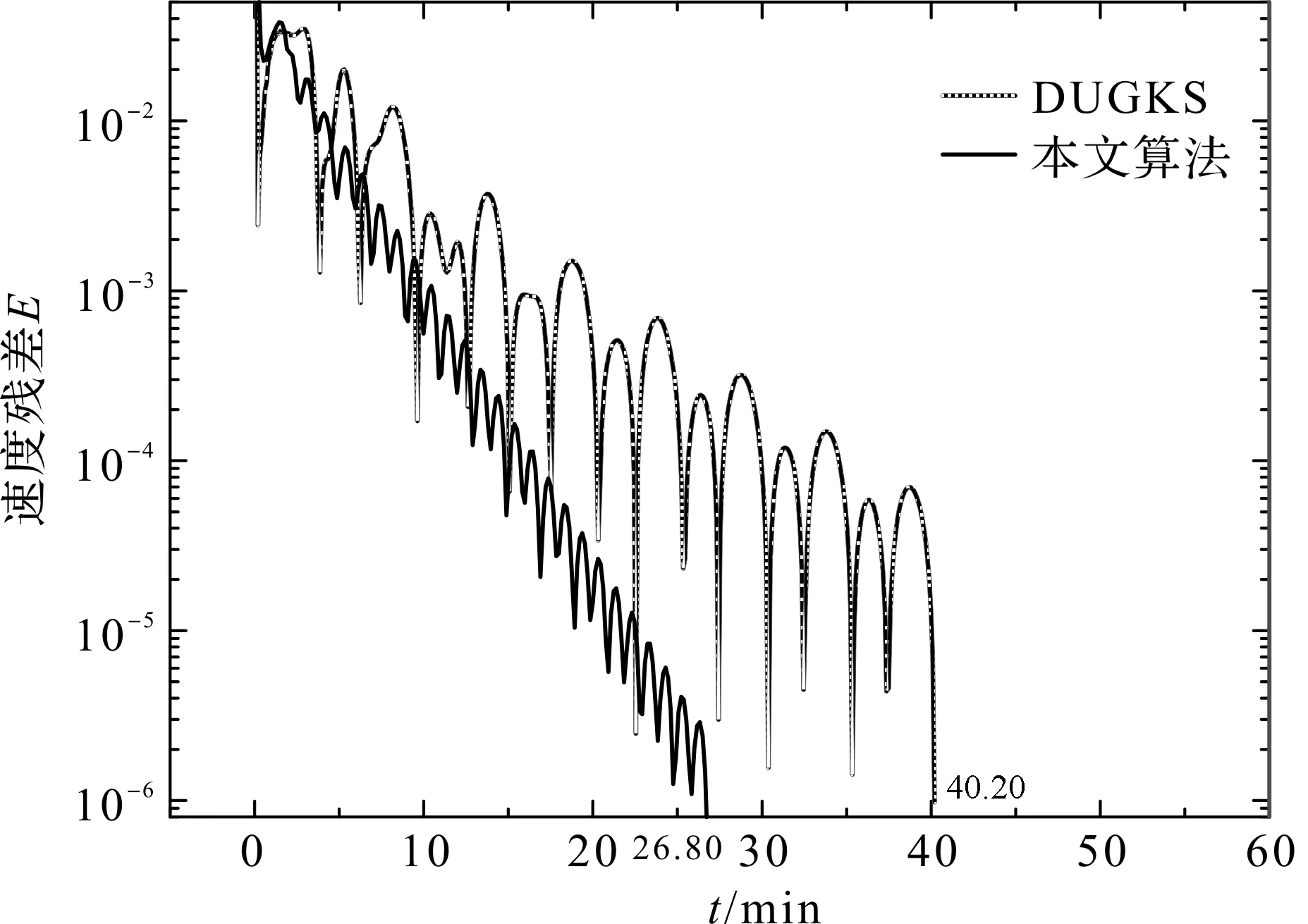
图7 不同算法的演化速度对比
本文算法、DUGKS算法达到相同终止条件时的演化速度如图7所示。从图7可以看出,本文算法的收敛速度明显快于DUGKS算法,2种算法达到终止条件所需时间分别为26.80 min和40.20 min。由此可见,本文算法在不改变DUGKS算法稳定性的前提下,提高了算法的计算效率,提升约30%。
3 结束语
针对于不可压热流体,本文基于DUGKS提出了一种简化算法。计算网格内微通量时,采用梯形公式代替原始算法中的中点公式,在保持原始算法的数值稳定性和精度下,有效解决了原始算法消耗较多计算资源的问题,提高了算法的计算效率。在低瑞利数情况下,本文算法的计算效率已取得不错的成绩,后续将在高瑞利数、复杂流体等方向展开进一步研究。
