钨基Heusler合金W2YZ的电子结构与磁性

费丽均，程 垚，赵路加，霍德璇

(杭州电子科技大学材料与环境工程学院，浙江 杭州 310018)

0 引 言

Heusler合金是一类金属间化合物，分子式为X2YZ型或XYZ型，前者称为全Heusler合金，后者称为半Heusler合金，其中X和Y是过渡金属元素，Z是Ⅲ，Ⅳ或Ⅴ族元素，由于它们的s-p电子的杂化状态，也被称为s-p元素。Heusler合金表现出十分丰富的物理特性，比如磁性半金属特性[1-2]、形状记忆效应[3-4]、拓扑绝缘体特性[5-6]等，并具有较高的居里温度，在自旋电子学、磁制冷、超导及热电转换等技术领域中具有巨大的应用潜力。

基于密度泛函理论的第一性原理计算可以高效快速地预测材料的物理性质。十多年来，研究人员在Mn2基，Co2基，Fe2基，Ni2基，Ti2基Heusler合金的研究中取得了许多成果。Rai等[7]计算研究了Co2TGe(T=Sc,Ti,V,Cr,Mn,Fe)的电子结构，指出Co2CrGe和Co2MnGe具有4 μB的整数磁矩，且具有较高的自旋极化率，有望应用于自旋电子学器件中。Huang等[8]采用全势线性缀加平面波的方法计算了Ti2CoGe的电子结构，指出其具有3 μB的整数磁矩和半金属铁磁性。近期，Zheng等[9]应用卷积神经网络的机器学习方法对Heusler合金材料的稳定性进行研究，预测存在一类新的W2基全Heusler合金，该类合金可能具有稳定的晶体结构，在自然界中可稳定存在，但还没有见到其物理性质的理论研究和实验结果的相关报道。因此，本文以该W2基Heusler合金为研究对象，运用基于密度泛函理论的第一性原理计算方法，系统地计算研究了W2YZ(Y=Mn,Fe,Co;Z=Si,Ge,Sn,Sb,Te)系列Heusler合金的晶体结构、电子结构和磁学性质，有望为自旋电子学器件研制中新型材料的选择提供研究参考。

1 计算过程中参数设置

采用WIEN2k[10]软件中实现的基于密度泛函理论(Density Functional Theory, DFT)的全势线性缀加平面波的方法进行计算，交换关联势用Perdew-Burke-Ernzerhof (PBE)参数化中的广义梯度近似(Generalized Gradient Approximation, GGA)。结构优化和自洽计算过程中的相关参数设置如下：原子球半径与最大波矢的乘积Rmt×Kmax取值为9；电荷密度傅里叶展开中最大到格矢量Gmax取值为14；第一布里渊区k点数取3 000个，得到简约第一布里渊区独立k点数104个；原子中核心电子与价电子间的截断能为-6 Ry。自洽循环计算的收敛条件为：电荷密度偏差小于1×10-4e/a.u.，总能偏差小于1×10-5Ry/原胞。

2 计算结果与讨论

2.1 晶体结构

Heusler合金X2YZ的常见结构有2种，分别为高度有序的Cu2MnAl型(L21型)立方晶体结构和Hg2CuTi型(XA型)反Heusler立方晶体结构。晶格中存在4个相互套构的fcc次晶格，原子占位的Wyckoff位置有4种，分别为A(0,0,0)，B(1/4,1/4,1/4)，C(1/2,1/2,1/2)，D(3/4,3/4,3/4)，如图1所示。s-p元素Z占据D位，根据其它2种过渡金属元素的原子占位的不同，可以得到2种高度有序的不同晶体结构。当同种元素X占据A和C位，Y占据B位时，形成L21结构。当A位和C位被不同元素分别占据时，形成XA结构。

分别计算不同晶体结构L21型和XA型下的15种W2YZ合金总能量随晶格常数的变化情况。其中合金W2MnSn在Birch-Murnaghan状态方程[11]拟合下的结果如图2所示。

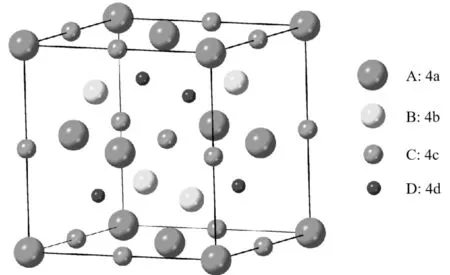
图1 Heusler合金在晶体结构中的4种占位

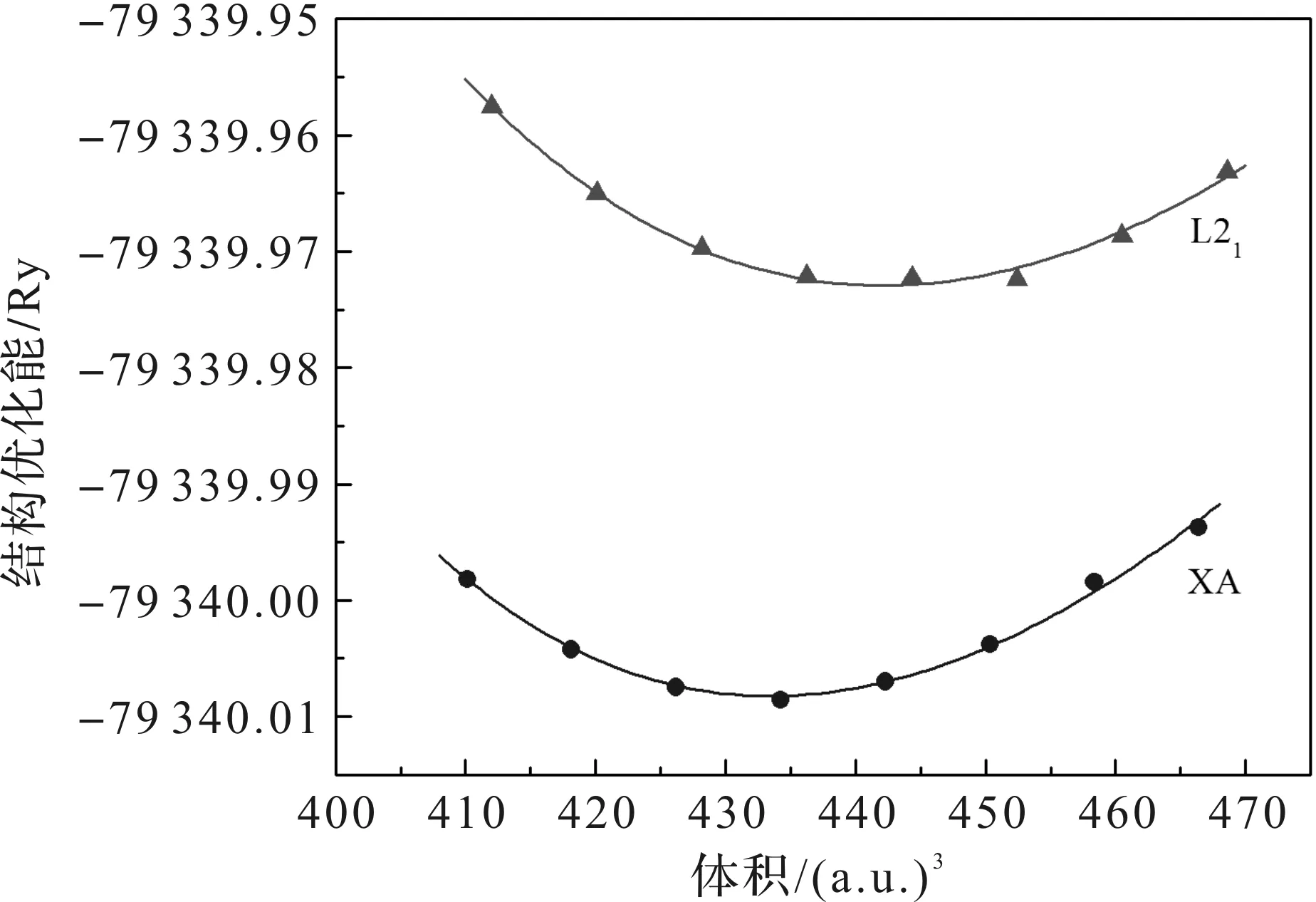
图2 不同结构下，W2MnSn合金能量随体积变化情况

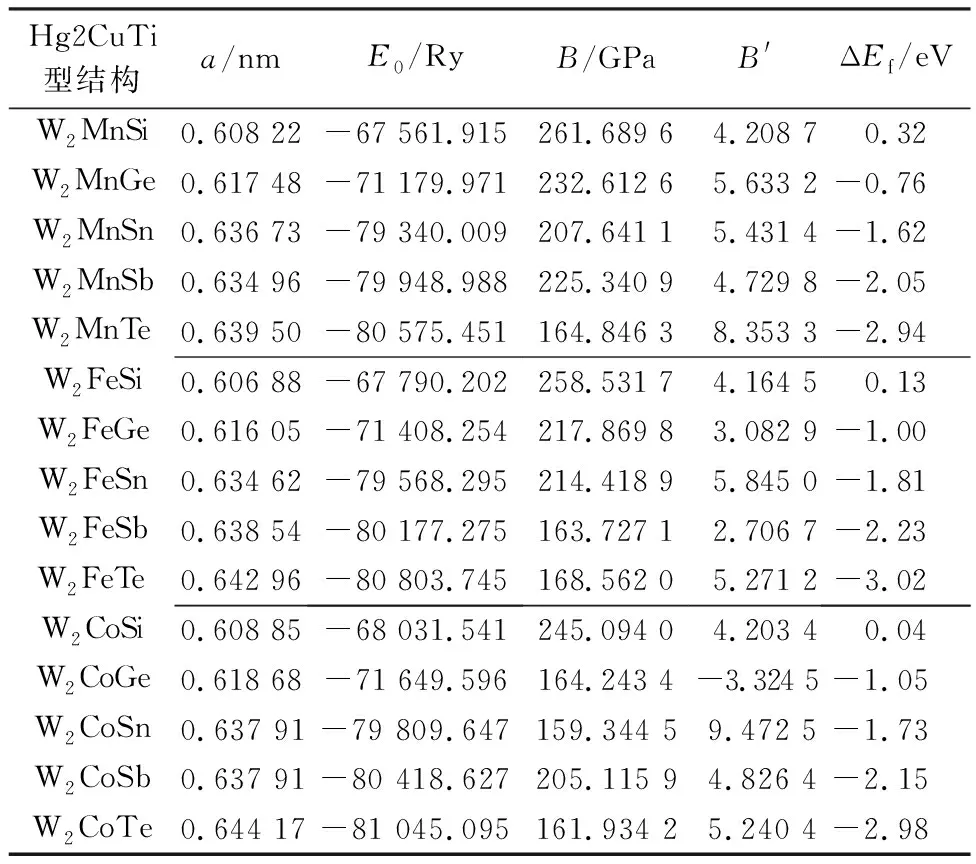
表1 结构优化后W2YZ合金的结构参数和ΔEf

由图2可以看出，XA型结构下的W2MnSn合金的晶胞总能量低于L21型结构下的晶胞总能，且XA型结构下的最低能量也低于L21型结构下的最低能量。在比较2种结构的稳定性时，由于同种物质在不同结构下的能量差是绝对的，而最低点处的能量值是相对的，所以可以忽略具体的能量差值，只比较两者在最低点处的能量[12]。由此得出，W2MnSn合金在XA型结构下更稳定。其余14种合金也有相同结果。因此，本文对W2YZ(Y=Mn,Fe,Co;Z=Si,Ge,Sn,Sb,Te)系列合金的电子结构和磁性计算均采用Hg2CuTi型结构。

为了进一步确定Hg2CuTi型结构下W2YZ合金的稳定性和合成的可能性，该系列合金化合物的形成能计算公式如下：

ΔEf(x,y,z)=E(x,y,z)-(Ex+Ey+Ez)

(1)

式中，E(x,y,z)表示W2YZ(Y=Mn,Fe,Co;Z=Si,Ge,Sn,Sb,Te)Heusler合金的平衡总能量，Ex，Ey，Ez分别表示其中每个元素x,y,z原子块体的平衡总能量。表1列出了W2YZ(Y=Mn,Fe,Co;Z=Si,Ge,Sn,Sb,Te)合金的形成能ΔEf，体积优化计算后得到的晶格常数a，最低能量E0以及对应的体积模量B和体积模量对压力的导数B′。

由表1可以看出，在W2MnZ(Z=Si, Ge, Sn, Sb, Te)，W2FeZ(Z=Si, Ge, Sn, Sb, Te)，W2CoZ (Z=Si, Ge, Sn, Sb, Te)这3个不同的体系中，随着s-p元素原子序数的增加，合金的晶格常数随之增大，而体系的总能量逐渐减少，晶体结构更稳定；当s-p元素相同时，15种合金的总能量随Mn，Fe，Co原子序数的增加依次减少，而晶格常数的变化较小，表明原子序数大的元素有更大的原子半径及更稳定的原子态，有利于形成稳定结构。

通过对W2MnZ，W2FeZ，W2CoZ体系中合金形成能的分析，可以发现，物质的形成能随s-p元素原子序数的增加逐渐降低。除了含Si的W2YSi(Y=Mn,Fe,Co)合金，其它Heusler合金的形成能皆为负值，表明这些合金具有稳定的晶体结构，有望在实验中合成。尤其是含Te的3种合金W2YTe(Y=Mn,Fe,Co)的总能量和形成能在这3个系列中都处于最小值，因此，W2YTe结构更稳定。实验合成本文所研究的15种合金化合物时，先从这3种合金着手应该更容易。

2.2 电子结构

通过计算W2YZ系列Heusler合金在平衡晶格常数下的电子性质得到的W2YZ(Y=Mn,Fe,Co;Z=Si,Ge,Sn,Sb,Te)合金的总态密度及分态密度如图3至图5所示。图3至图5中，正值表示电子自旋向上，负值表示电子自旋向下，0 eV处的实线EF代表费米能级。图中主要考察的是W的5d轨道、Mn/Fe/Co的3d轨道和Si/Ge/Sn/Sb/Te的s及p轨道对总态密度的影响。

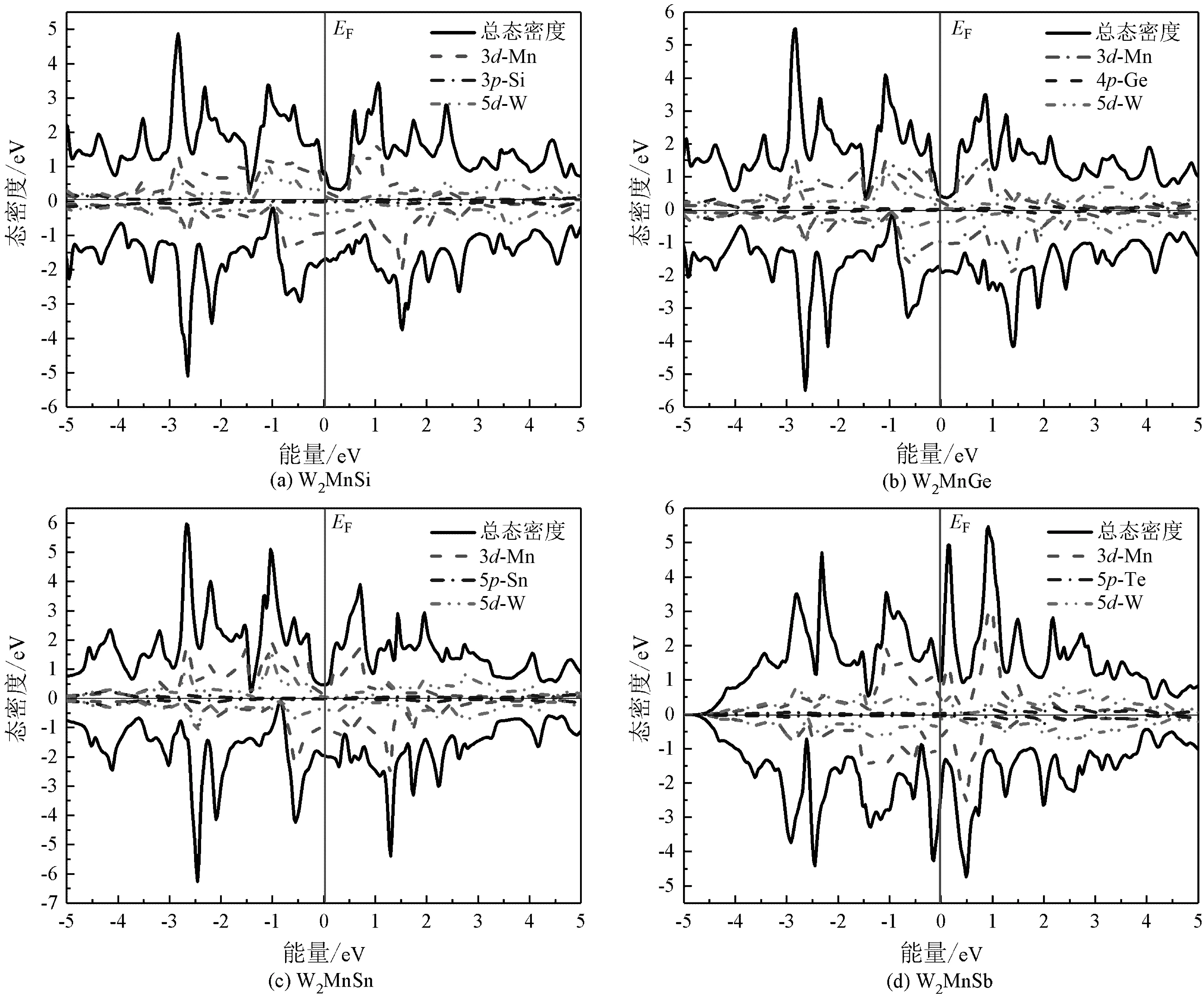
图3 W2MnZ(Z=Si,Ge,Sn,Sb)在平衡晶格中的总态密度及分态密度

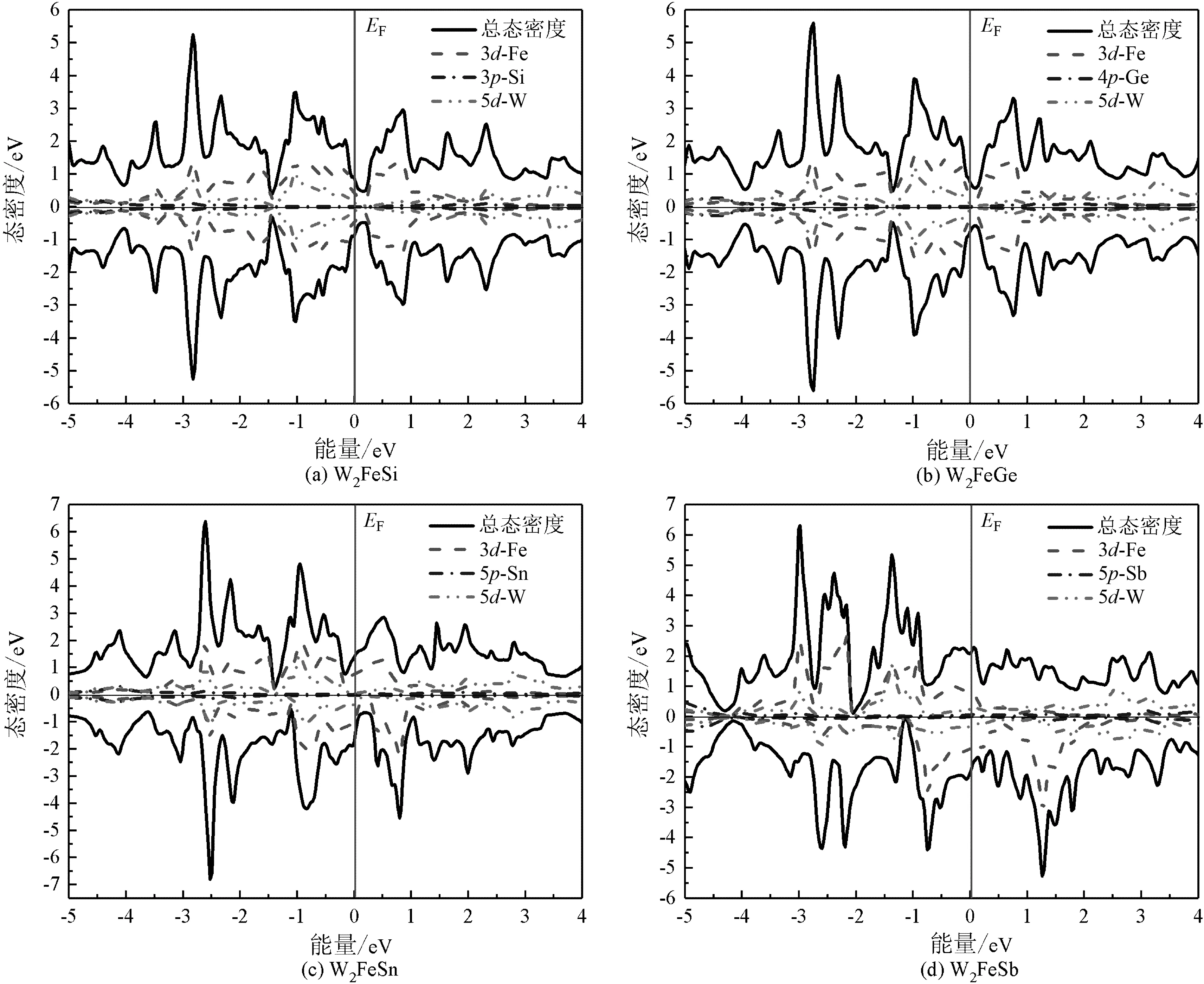
图4 W2FeZ(Z=Si,Ge,Sn,Sb)在平衡晶格中的总态密度及分态密度

图5 W2CoZ(Z=Si,Ge,Sn,Sb)在平衡晶格中的总态密度及分态密度

从图3至图5可以看出，由于W2YZ(Y=Mn,Fe,Co;Z=Si,Ge,Sn,Sb,Te)合金中含有Mn，Fe和Co这3种磁性原子，因此合金在费米能级附近的自旋向上和自旋向下电子的总状态密度不对称，2个自旋方向上的态密度不能相互抵消，在能量上存在位移，这是由于磁性金属的交换作用导致的，因此合金具有磁性特征。而W2FeSi和W2FeGe合金在平衡态下具有对称的总状态密度，自旋向上及自旋向下的态密度相加时为0，表明自旋电子在2个方向上的数量相同[13]，如图6所示。综上所述，在本文研究的计算条件下，W2FeSi和W2FeGe合金表现为非磁性特征。

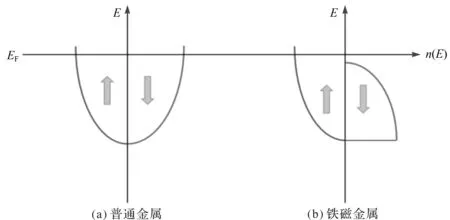
图6 普通金属和铁磁金属的状态密度示意图[13]

图3至图5的结果表明，W2MnZ(Z=Si,Ge,Sn,Sb)，W2FeZ(Z=Si,Ge,Sn,Sb)，W2CoZ(Z=Si,Ge,Sn,Sb)这3个系列的Heusler合金具有相似的电子态密度变化规律，在所讨论的[-5,5]的能量区间内，合金的总态密度主要来源于Mn/Fe/Co的3d电子态与W的5d电子态之间的强烈杂化，s-p元素的贡献比较小。3个系列的Heusler合金中费米能级随着s-p元素原子序数的增加向低能量区域移动。由于在不同的体系中金属元素与重金属元素的电子杂化强度不同，从而导致合金在费米能级附近的能态劈裂程度不同，具体表现为W2MnZ(Z=Si,Ge,Sn,Sb)合金在自旋向上方向上费米能级附近具有类半金属带隙，总能量低于自旋向下方向上的能量；W2CoZ(Z=Si,Ge,Sn,Sb)合金在电子自旋向下时3d-Co的电子态更稳定，因此在费米能级附近具有较低的能量，自旋极化率较高。所有合金的自旋向上及自旋向下态密度图的费米能级附近都不存在带隙，表明该类合金在平衡态下均不表现磁性半导体或磁性半金属特性。W和Te的原子量较高，具有较强的自旋轨道相互作用，因此，对该类合金，尤其是同时含有W和Te 2种原子的W2YTe(Y=Mn,Fe,Co)合金，可进行自旋轨道相互作用的进一步研究。

2.3 能带分析

为了更直观地反映W2YZ的电子性质，在自洽计算的基础上，计算了合金的能带结构。考虑到态密度计算显示W2FeSi合金是非磁性的，2.1节中的结构优化计算表明W2CoTe合金具有较低的总能量，因此，本文选取W2FeSi和W2CoTe合金，对它们的能带结构展开研究分析。W2FeSi和W2CoTe合金的能带结构如图7所示，图7中，实线表示电子自旋向上时的能带结构，虚线表示自旋向下方向的能带结构，0 eV处的实线EF代表费米能级。

从图7可以看出，W2CoTe合金的电子自旋向上和自旋向下的能带结构存在明显差异，表现出磁性特征；而W2FeSi合金在2个自旋方向上的能带结构完全相同，表明W2FeSi合金是非磁性的。不管是W2FeSi合金还是W2CoTe合金，在2个自旋方向上的费米能级附近的能带均不存在带隙，说明它们不具有半导体或半金属特性。对于W2CoTe合金而言，其费米面附近的自旋向上的能态具有类半金属特征，由于其含有相对原子质量较高的W和Te原子并具有相对稳定的晶体结构，所以，可以用自旋轨道耦合的方法对它的磁性及半金属性做进一步研究分析。

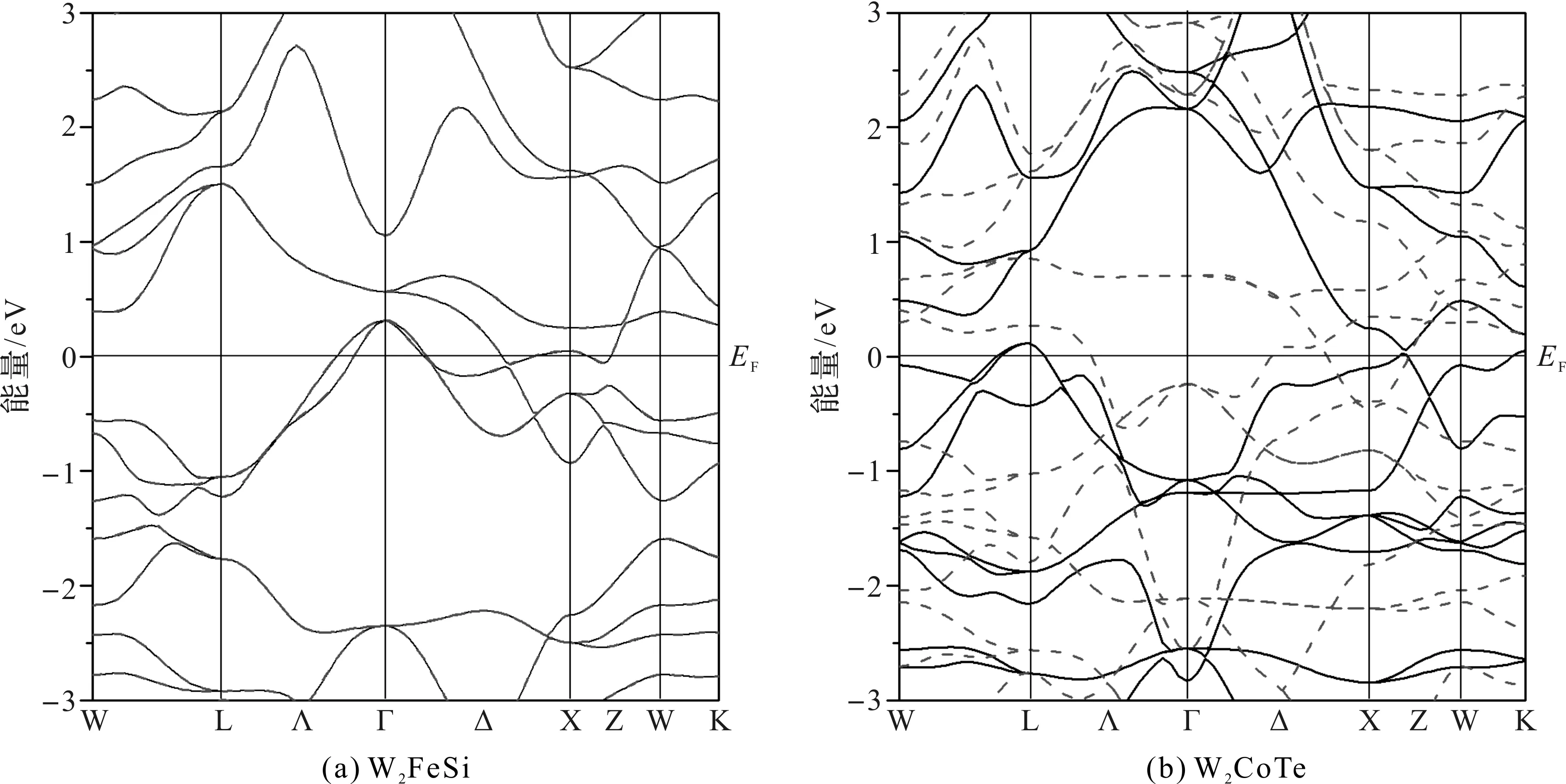
图7 W2FeSi和W2CoTe合金的能带结构

2.4 磁性与Slater-Pauling规则

为了更好地分析W2YZ(Y=Mn,Fe,Co;Z=Si,Ge,Sn,Sb,Te)合金的磁学性质，表2列出了W2YZ系列合金的总磁矩及每个原子的局域磁矩。表2中，X表示过渡金属原子，M表示本文计算得到的合金化合物的总磁矩，Zt表示合金的总价电子数，Mt表示合金化合物的总磁矩，根据Slater-Pauling规则[14](Mt=Zt-24)得到Mt。

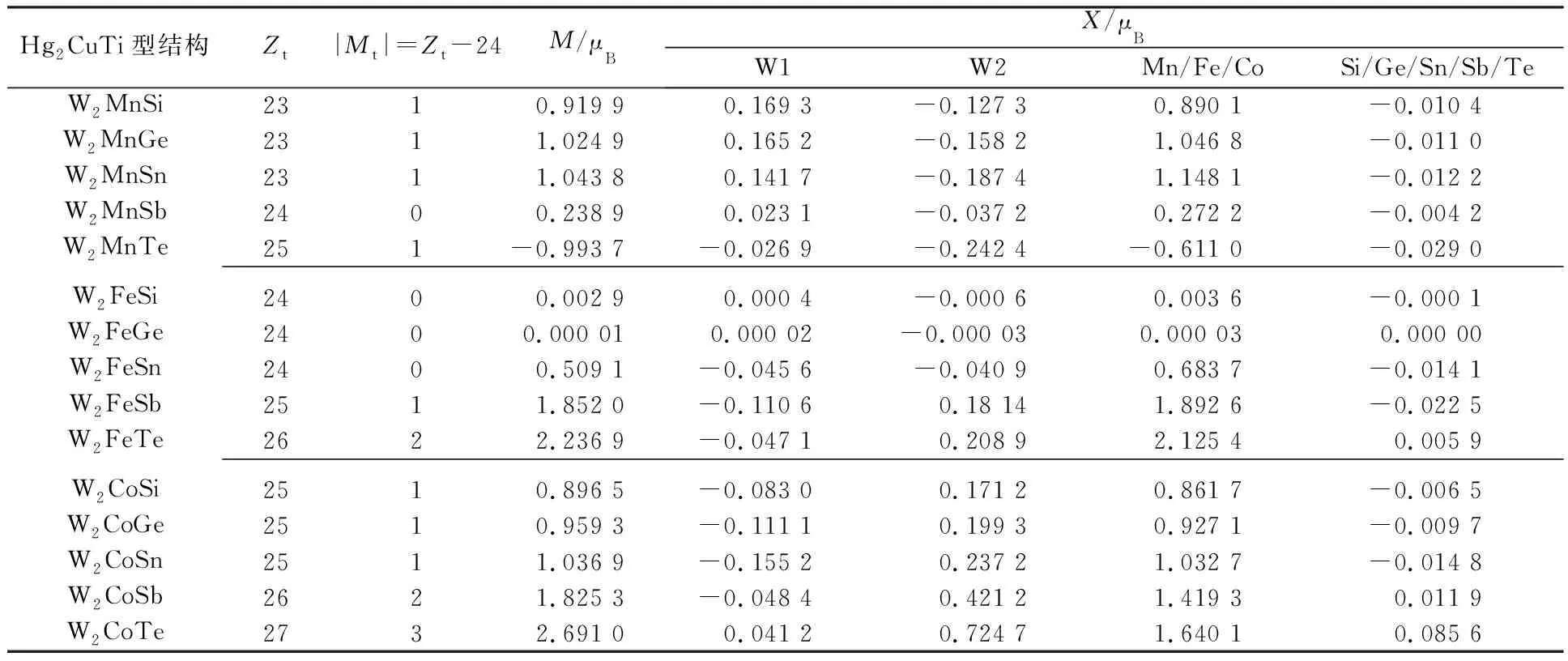
表2 W2YZ合金的总磁矩及局域磁矩

由表2可以看到，W2MnZ(Z=Si,Ge,Sn,Te)，W2FeZ(Z=Si,Ge)，W2CoZ(Z=Si,Ge,Sn)合金具有整数倍的玻尔磁矩，满足Slater-Pauling规则；而W2MnSb，W2FeSn，W2FeSb，W2FeTe，W2CoSb和W2CoTe几种合金的磁矩则偏离总价电子数减去24的Slater-Pauling规则的直线，不为整数磁矩，这与本文对其状态密度的分析结果一致。在研究的一系列合金中，3d过渡金属元素(Mn/Fe/Co)对总磁矩有着较大的贡献，而5d金属元素W和主族s-p元素的贡献比较小，可以忽略。在多数情况下(如W2MnZ系列中)，s-p元素与其他元素原子磁矩成反平行排列。

根据计算得到的15种Heusler合金的总磁矩与根据Slater-Pauling规则拟合所得的曲线如图8所示。从图8可以看出，计算得到的系列合金与Slater-Pauling规则之间的差距，其中W2MnZ(Z=Si,Ge,Sn,Te)，W2FeZ(Z=Si,Ge)，W2CoZ(Z=Si,Ge,Sn)合金在Mt=Zt-24的直线上，总磁矩遵循Slater-Pauling规则。而W2MnSb，W2FeSn，W2FeSb，W2FeTe，W2CoSb和W2CoTe合金则位于直线之外，不满足Slater-Pauling规则。

图8 W2YZ(Y=Mn,Fe,Co;Z=Si,Ge,Sn,Sb,Te)合金总磁矩与Slater-Pauling的比较

3 结束语

本文运用WIEN2k程序计算了W2MnSn合金在Cu2MnAl型和Hg2CuTi型不同构型下的结构稳定性，得到这类合金的稳定晶体结构为Hg2CuTi型。并在此结构建立晶体模型上，计算了一系列Heusler合金W2YZ(Y=Mn,Fe,Co;Z=Si,Ge,Sn,Sb,Te)在Hg2CuTi构型中的形成能、电子结构和磁性。实验结果表明，W2YTe(Y=Mn,Fe,Co)合金在平衡晶格常数下具有最低的总能量以及负的形成能，结构更稳定，可以在工业制备这3种合金过程中自发形成；W2YZ(Y=Mn,Fe,Co;Z=Si,Ge,Sn,Sb,Te)合金在平衡状态下具有良好的金属性，是一类具有实际应用价值的新型导电材料，并且W2MnZ(Z=Si,Ge,Sn,Te)，W2FeZ(Z=Si,Ge)，W2CoZ(Z=Si,Ge,Sn)等9种Heusler合金具有整数倍的总磁矩，其值遵循Slater-Pauling规则，在平衡晶格常数下的自旋极化率高于普通金属，有望作为自旋注入材料应用于自旋电子器件中。本文研究的系列Heusler合金的有关结果为磁性材料的研究提供了理论参考。