基于稀疏注意力的自适应图池化方法

朱小草，郭春生，张宏宽，金昊炫

(1.杭州电子科技大学通信工程学院，浙江 杭州 310018；2.数源科技股份有限公司，浙江 杭州 310012；3.浙江农业科学院，浙江 杭州 310021)

0 引 言

现实世界中，很多数据以图结构的形式存在，如社交网络、电商网络、生物网络和交通网络等。图由节点和边组成，作为一种非欧几里得形数据，其主要应用有节点分类、图分类和链路预测等。目前，关于图卷积网络(Graph Convolutional Network, GCN)[1]的研究比较多，但图池化的相关研究相对少。早期的图池化通常是汇总图中的所有节点表示，比如文献[2]采用完全二叉树实现池化算子，在最粗糙的层上对节点进行任意排序，在平衡二叉树中将这种排序传播到较低的层次，最终在最低层上产生一个规则的排序；文献[3]进行重排操作，根据节点在图中的结构将节点重新排列到更有意义的顺序；文献[4]将图神经网络(Graph Neural Network, GNN)视为消息传递策略，提出一种通用的图分类框架，采用Set2Set方法获得整个图的表示。但是，通过上述方法得到的图表示是“扁平的”，没有考虑结构信息。文献[5]使用2个GNN对节点进行集群，重新定义图池化模块，使用上一层GNN的输出结果对节点进行聚类或池化，但由于GNN计算的软分配矩阵是稠密的，因此不适用大型图；文献[6]通过自适应地选择节点的子集来完成池化，使用一个可学习的向量将所有节点特征投影到1维，然后通过k-max池化选择节点，但没有考虑图的结构，只能从特征这一个方面来评价节点的重要性，方法过于简单；文献[7]运用k-max池化并保持稀疏性，占用内存较小，但其精度相对较低；文献[8]提出一种基于傅里叶变换的池化方法，但其性能取决于特征向量的个数，计算复杂较高；文献[9]基于注意力机制，通过结构和属性信息为每个节点得到一个标量并进行排序，根据排序结果保留最重要的一部分节点及其连边进而完成池化操作，但其不聚合节点信息，无法有效保留节点和边信息；文献[10]对文献[9]进行了改进，将注意力值作为边的权重进行加权聚合，但在聚合节点信息时容易造成节点特征过于平滑，信息丢失较多，图分类效果不佳。针对图在池化过程中存在不能较好保留局部特征、计算复杂度高等问题，本文提出一种基于稀疏注意力的自适应图池化方法(Adaptive Graph Pooling based on Sparse Attention，AGP-SA)，在形成集群时，自适应地在一阶范围内选择重要节点从而减少了信息损失，并降低了计算复杂度。

1 基于稀疏注意力的自适应图池化方法

1.1 图池化方法模型

本文提出的基于稀疏注意力的自适应图池化方法AGP-SA的流程如图1所示。模型由集群形成和集群采样组成。集群是指一组节点所构成的集合，集群中的节点特征相似。

图1 AGP-SA算法图池化流程

集群形成主要是通过稀疏注意力自适应地选择相似度高的节点形成集群。首先，在注意力机制中加入图结构信息权重，使之与节点特征相结合，增加相连节点之间的相似性；然后，计算出其一阶邻域内节点之间的相似性得分；最后，运用sparsemax[11]将注意力值进行稀疏化从而得到分配矩阵，最终得到每个集群的节点构成。

集群采样是通过局部聚合卷积函数聚合节点得到集群表示，并计算每个集群的信息量，采用TopK选择分数较高的集群。然后通过分配矩阵重新计算图的邻接矩阵，获得最终池化后图的特征矩阵和邻接矩阵。

1.2 集群形成

通过稀疏注意力来形成集群，利用图的特征信息和结构信息得到节点隶属于某个集群的强度，对于那些强度较小的，即与集群内的其它节点差异较大的节点，通过注意力稀疏化将其剔除，由此形成的集群是内部距离较小、集群间距离较大的节点，这样有助于保留图的局部特征，进行节点聚合时不会造成过平滑。

本文采用文献[10]中的相似度计算方法，先将2个节点的特征向量进行拼接，再将拼接好的向量与1个可学习的权重向量做点积，最后使用激活函数保持函数的非线性。此外，为了保持图的结构性，增加了图的结构特征，因此，节点i和节点j之间的相似注意力为：

(1)

为了使注意力分数在不同节点之间易于比较，需要对其进行归一化处理。经常采用的方法是softmax。由于softmax的输出都大于0，故所有邻节点都对当前节点进行了消息传递，因此，在一阶邻域中选出相似度高的节点来形成集群有利于保留图的局部特征。因此，本文引入softmax的稀疏化形式sparsemax。对注意力数值求1个阈值，在阈值以下的数设置为0，对阈值以上的数进行归一化，即在一阶范围内选择相似度高的节点形成集群。

令si为ei进行归一化后的向量，其中ei为节点i的注意力值，即ei=[ei,1,ei,2,…,ei,N]。ΔN-1={si∈RN|1Tsi=1,si≥0}表示维度为N-1的单纯形。使用sparsemax产生稀疏的概率分布：

(2)

在真实分布未知的情况下，式(2)的函数形式并不能直接求解。因此，定义拉格朗日函数：

(3)

(4)

(5)

(6)

综合上述，式(3)对偶形式为：

(7)

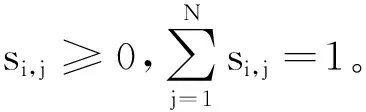
综上，可以使用sparsemax来形成分配向量si，对一阶邻域内相似度高的节点赋予较大的权重，相似度较低的赋予较小的权重，对于极低的直接将其置为0。稀疏注意力可以自适应地选择节点形成集群，具有集群内距离小、集群间距离大的特点，更好地保留了图的局部特征。

1.3 集群采样

通过局部聚合卷积函数对集群进行采样，在节点聚合时只选取集群内的节点。为了在池化过程中减少信息损失，需要保留局部信息较多的集群。将稀疏注意力与局部聚合卷积结合起来可以保留图的局部特征，从而在采样时保留原图中较多的信息量，使得图分类结果更加精确。

(8)

将适应度向量Φ=[φ1,φ2,…,φΝ]T与集群表示矩阵SX相乘：

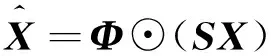
(9)

(10)

(11)

(12)

2 仿真实验结果与分析

2.1 实验数据集

仿真实验在图分类数据集PROTEINS，NCI1，NCI109和FRANKENSTEIN上进行。PROTEINS是蛋白质图数据集，数据集中节点表示氨基酸，标签表示蛋白质是否为酶。NCI1和NCI109是用于抗癌活性分类的数据集，数据集中每个图都是一个化学化合物，其节点和边分别代表原子和化学键，标签为化合物中是否有阻碍癌细胞增长的性质。FRANKENSTEIN是一组分子图，其节点特征包含连续值，标签表示分子是否为诱变剂。各类实验数据集统计特性如表1所示。

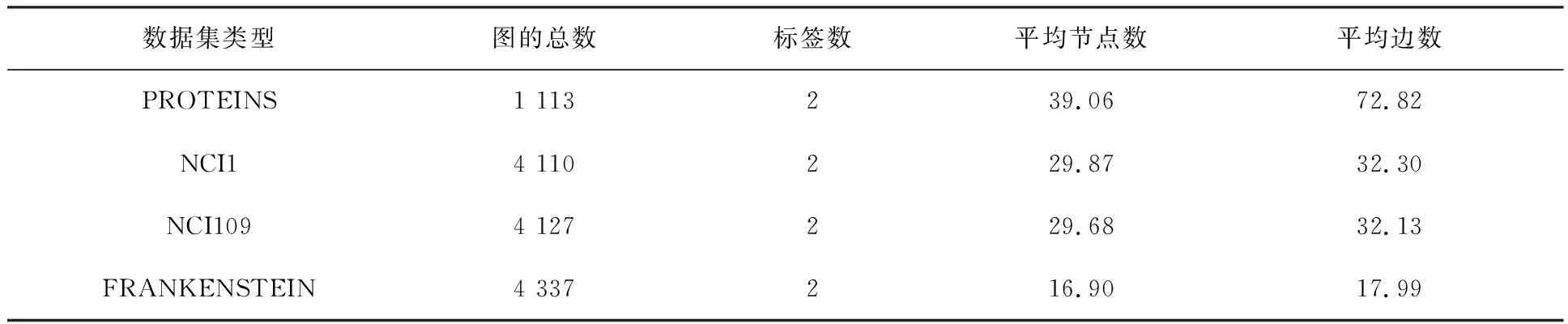
表1 实验数据集统计特性

2.2 实验设计

每个数据集中，80%用于训练，10%用于验证，10%用于测试。采用十折交叉验证法在10个随机种子上进行实验，共得到100个测试结果，对其取平均值得到每个数据集上的最终精度。实验中，PROTEINS，NCI1，NCI109和FRANKENSTEIN的隐层维度分别为64，128，128和32，其学习率分别为0.010，0.010，0.010和0.001。从表1可以看出，在FRANKENSTEIN数据集中，节点数和边数均比其他数据集少，说明图的结构更加简单，因此要设置更小的学习率。每50个epochs后，学习率衰减为之前的0.5倍，权重衰减设为5e-4，使用Adam优化器，池化比率k均为0.5，模型训练100个epochs后得到测试结果。

2.3 实验结果与分析

2.3.1 不同图池化方法正确率比较

分别采用DiffPool[5]，TopK[6]，SAGPool[9]，ASAP[12]和本文方法在4个数据集上进行实验，得到图分类结果如表2所示。表2中，“±”后的数字为10个随机种子正确率的方差，其中DiffPool，TopK，SAGPool中的实验数据来自原文。

表2 不同图池化方法识别正确率 单位：%

从表2可以看出，本文提出的AGP-SA方法的识别正确率高于其他方法，对比DiffPool，TopK，SAGPool方法，在所有数据集上分别平均提升了9.16%，4.51%，3.71%，因为AGP-SA方法兼具了分配矩阵稀疏化，与图的结构信息相结合，聚合了节点信息的特点，其方差相差更小，在训练时更稳定。对比ASAP方法，AGP-SA方法的识别正确率在PROTEINS，NCI1和NCI109数据集上分别有0.83%，0.62%和1.18%的提升，在形成集群时，ASAP方法中采用softmax，采样集群包含所有一阶邻节点，而AGP-SA通过自适应选取相似度高的一阶邻节点形成集群，有利于保留图的局部特征，在采样时能减少信息损失，从而使图分类准确率更高。此外，由于FRANKENSTEIN数据集的每张图的节点数和边数相对较少，在形成集群时更加稀疏，集群中所包含的节点信息偏少，所以提升效果不大，说明AGP-SA方法对复杂数据集的普适性更好。

2.3.2 不同模型变体正确率比较

采用本文AGP-SA方法及其2种变体在4个数据集上进行实验，得到图分类结果如表3所示。其中AGP-SA(softmax)表示在集群形成中的归一化用softmax代替sparsemax，AGP-SA(GCN)表示在集群采样时用GCN代替局部聚合卷积。AGP-SA表示使用sparsemax和局部聚合卷积。

表3 不同AGP-SA变体的识别结果 单位：%

从表3可知，对比AGP-SA(softmax)，AGP-SA的识别正确率平均提升了1.60%，说明将注意力稀疏化有助于节点特征的保留，在后续集群采样时减少信息损失，从而提高了图分类的准确率。对比AGP-SA(GCN)，AGP-SA的识别正确率平均提升了2.90%，说明局部聚合卷积可以更加精确地学习其潜在的复杂结构，将局部和全局结合起来能更准确地量化每个集群所包含的信息。

2.3.3 不同参数正确率比较

选取不同的权值λ，采用本文AGP-SA方法在4个数据集上进行实验，得到图分类结果如表4所示。

表4 不同权重λ下的AGP-SA识别结果 单位：%

从表4可以看出，λ为0.25时，数据集FRANKENSTEIN取得的效果最佳；λ为0.50时，其它2个数据集的效果最佳。而λ表示的是在计算注意力分数时图结构所占的权重参数，因此对于简单的图来说，在计算节点之间的相似度时，其节点特征信息比结构信息更重要。

图2 不同池化比率k的结果比较

选取池化比率k分别为0.125，0.250，0.375，0.500，0.625，0.750，0.875和1.000，采用AGP-SA方法在数据集PROTEINS上进行实验，得到图分类结果如图2所示。

从图2可以看出，当池化比率k为0.500时，数据集PROTEINS的识别准确率最高。当k小于0.500时，池化比率越小，其分类识别准确率也越小。因为图中所保留的节点过少，导致图的特征信息丢失过多，也使得图的结构信息不完整，因此其性能下降。当k大于0.500时，其准确率总体呈现为下降趋势，因为过多的节点保留会造成信息的冗余，因此最终选择池化比率为0.500。其过小会丢失结构信息。

图3 不同邻域阶数h的结果比较

本文在形成集群的过程中，计算相似注意力时选取了范围为一阶内的邻节点，为了说明选择此邻域阶数的理由，选取h分别为1，2，3和4，采用AGP-SA方法在在数据集PROTEINS上进行实验，得到图分类结果如图3所示。

从图3可以看出，当形成集群的范围为1阶时，识别准确率最高，且阶数越多。当邻域选取范围过大时，造成图信息的冗余，导致图分类的性能变差。形成集群时的选取原则是选择相似度高的节点，本文运用稀疏注意力在一阶邻域范围内进行再次筛选，使得集群内的节点相似度更高，因此集群内距离小，集群间距离大，使得采样保留更丰富的图信息。而ASAP中所形成的集群包含了一阶邻域内的所有节点，造成节点过拟合，不能有效保留图的局部特征信息，导致分类性能不佳。所以，注意力的稀疏化能够改善节点过拟合的局限性。

3 结束语

本文将稀疏注意力和局部聚合卷积结合在一起，提出一种基于稀疏注意力的自适应图池化方法。仿真实验表明，sparsemax可防止节点特征过平滑，局部聚合卷积可有效提取图中局部重要节点信息，从而提升图分类准确率，当集群邻域范围为1阶和池化比率为0.5时，准确率最高。但是，本文所提方法只适用于简单的同质图，难以扩展到节点类型或关系类型多于一种的异构图中，限制其应用范围，后续将尝试在异构图中展开进一步研究。