基于狄利克雷过程高斯混合模型的变分推断
2021-09-29万志成
万志成,郑 静
(杭州电子科技大学经济学院,浙江 杭州 310018)
0 引 言
高斯混合模型(Gaussian Mixture Model,GMM)是一种常用的统计建模工具,通过多个高斯分量混合来描述一个复杂的数据分布,具有易处理的概率密度函数,可以得到显式表达式,广泛应用于机器学习和数据挖掘等领域。马敬山等[1]将GMM与反向传播神经网络(Back Propagation Neural Network, BPNN)结合起来,提出一种针对质谱数据的三分类模型。欧丰林等[2]融合GMM和深度学习算法实现了高效目标跟踪。何冰倩等[3]运用改进的GMM对视频中的人体动作进行识别,扩展了GMM的使用场景。然而,在有限的高斯混合模型建模过程中,需要确定适当数量的混合分量,分量个数过多或过少都会导致过拟合或欠拟合。解决GMM选择问题的主要方法包括确定性方法和贝叶斯方法。确定性方法主要是在期望最大化(Expectation Maximization, EM)框架下,通过极大似然估计来优化模型的似然函数[4]。贝叶斯方法中,最常用的是选定贝叶斯信息准则(Bayesian Information Criterion, BIC)来确定模型的复杂度[5]。上述2种方法都是通过比较多个模型的复杂度来选择模型,可能导致过拟合或欠拟合。与之不同的非参数贝叶斯方法则通过拟合单个模型,并根据观测数据来调整自身复杂度,避免手动进行模型选择的同时加快了收敛速度[6-7]。Rasmussen[8]将有限高斯混合模型与狄利克雷过程结合起来,提出一种无限高斯混合模型,并通过蒙特卡洛马尔可夫链(Markov Chain Monte Carlo, MCMC)来解决模型参数的估计问题。尽管MCMC方法能有效估计参数,但收敛速度较慢,计算成本过高。变分贝叶斯方法作为一种强大的确定性近似技术,计算成本小,收敛速度快,近年来备受关注。其基本思想是通过一类易处理的分布族来近似隐变量的后验分布,并通过最大化对数似然函数下界得到模型的参数估计。狄利克雷过程作为非参数贝叶斯统计中的重要方法,最常见的应用是作为狄利克雷过程混合模型的先验。Blei等[6]给出了狄利克雷过程混合模型变分推断的范式表达,奠定了狄利克雷过程混合模型变分推断的基础。Bishop[9]给出了有限多元高斯混合模型的变分推断过程,完整阐述了多元高斯混合模型的变分推断过程。Lim等[10]给出了无限一元高斯混合模型的变分贝叶斯推断过程。本文结合多元高斯混合模型与狄利克雷过程先验,给出无限多元高斯混合模型的表达式,并提出一种高效的变分贝叶斯算法,用于解决模型选择和参数估计问题。
1 无限高斯混合模型及其算法
1.1 无限高斯混合模型
给定混合分量个数K,有限高斯混合模型的概率密度函数为:
(1)

当式(1)中的K值趋向于无限大时,高斯混合模型由有限变成无限。无限高斯混合模型的密度函数如下:

(2)

(3)
如果随机概率测度G的分布由狄利克雷过程DP(a,G0)产生,则记为G~DP(α,G0)。同时,G可以通过以下的截棍过程进行构造:
(4)

(5)

本文引入狄利克雷过程先验,根据狄利克雷过程的截棍构造式(4),是V的函数。因此式(3)改写为:
(6)
在贝叶斯的理论框架下,需要指定模型其余参数的先验分布。Vk的先验分布为标准的贝塔分布,表示为:
(7)
参考文献[9]对u和Λ的先验设置,其先验分布为:
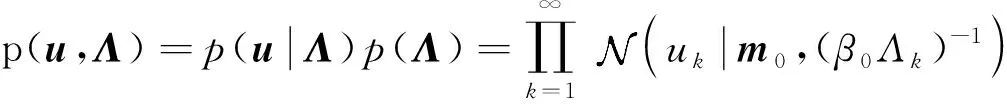
(8)

根据式(6)、式(8)的先验设置,得到X在隐变量{Z,u,Λ}下的条件分布为:
(9)
无限高斯混合模型中各随机变量的关系如图1所示,其中圆圈表示随机变量,有向箭头表示变量之间的关系。根据贝叶斯规则,将式(6)—式(9)整合起来,得到观测值X和各个隐变量Θ={Z,u,Λ,V}的联合密度函数为:
p(X,Θ)=p(X,Z,V,Λ,u)=p(X|Z,u,Λ)p(Z|V)p(V)p(u|Λ)p(Λ)
(10)

图1 无限高斯混合模型中各随机变量的关系
1.2 变分贝叶斯推断
贝叶斯推断主要是根据先验分布计算出隐变量的后验分布,但由于大部分模型结构过于复杂,常常使得后验分布难以计算。因此,本文运用变分贝叶斯推断方法来近似后验分布。变分推断的核心思想是选择一族易处理的分布族Q(Θ)来近似真实后验分布p(Θ|X)。其中变分后验Q(Θ)可以通过最大化变分下界L(Q)得到:
(11)
为了获得变分下界的最大值,假定近似真实后验分布Q(Θ)可以进行因式分解,Q(Θ)分解为:
(12)
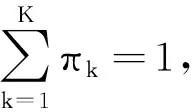
对于式(12)中的元素Qj(Θj),其最优的一般表达式为[9]:
lnQj(Θj)=Ei≠j[lnp(X,Θ)]+C
(13)
其中,C表示常数项。
1.2.1Q(Z)的变分推断
根据截断点K的设置和式(13)可以得到:
(14)
由于指数分布族的特点,lnQ(Z)的先验分布和后验分布形式相近。因此将式(14)进行拆分,并进行合并同类项,可得:

(15)
通过式(14)可以得到:
(16)

(17)
式中,
(18)
对于离散分布Q(Z)而言,可以获得E(Znk)=rnk。
1.2.2 Q(V)的变分推断
根据式(13)可以得到:
(19)
(20)
(21)
1.2.3 Q(u|Λ),Q(Λ)的变分推断
根据式(13)可以得到:

(22)
进一步可得:
(23)
(24)
(25)
(26)
根据推导出的更新方程,得出参数Θ期望如下:
Ez(Znk)=rnk
(27)

(28)

(29)
(30)
(31)

1.2.4 变分下界L(Q)
根据式(14)、式(19)和式(22),可以直接计算得出下界式(11)。在实际应用中,可通过观察下界L(Q)的值来控制迭代的次数,直到L(Q)收敛时停止迭代。
对于无限高斯混合模型,其下界为:

(32)

(33)
(34)
(35)

(36)
(37)
(38)
(39)
本文提出的无限高斯混合模型变分贝叶斯算法主要是通过不断迭代超参数直到变分下界收敛。将Vk的后验均值作为其参数估计带入到式(2),求解出相应的混合比例系数,将其中小于10-5的系数删除,从而自动选择最优分量个数。同时,根据mk与Λk后验分布参数计算相应期望,将其作为参数mk和Λk的估计值。无限高斯混合模型的变分贝叶斯算法如下。

输入:数据X,截断点K(1)初始化超参数α0,m0,β0,W0,v0,通过K-means算法初始化Ez(Znk)(2)根据式(18)、式(20)、式(21)、式(23)—式(26)更新超参数mk,βk,Wk,vk,pk,qk(3)根据式(27)—式(31)更新期望值(4)计算得到当前的下界L(Q)(5)重复步骤2—步骤4,直至L(Q)变化值小于10-3时,退出循环(6)输出各个超参数以及最终的L(Q)值(7)计算Ev(Vk)=pk/(pk+qk),将其作为Vk的值代入式(2)中计算得出k(8)将混合比例中小于10-5的值删去,从而得到真实K值(9)根据mk与Λk后验分布参数计算相应期望,将其作为参数mk和Λk的估计值(10)整合步骤7—步骤9中mk,Λk,k输出值,得到参数u,Λ,的估计值
2 数值模拟及分析

首先,由不同参数的高斯混合模型生成3个有1 000个样本点的数据集。其次,运用本文提出的变分贝叶斯算法对3个数据集进行20次模拟,取其平均值作为参数估计值,结果如表1所示。
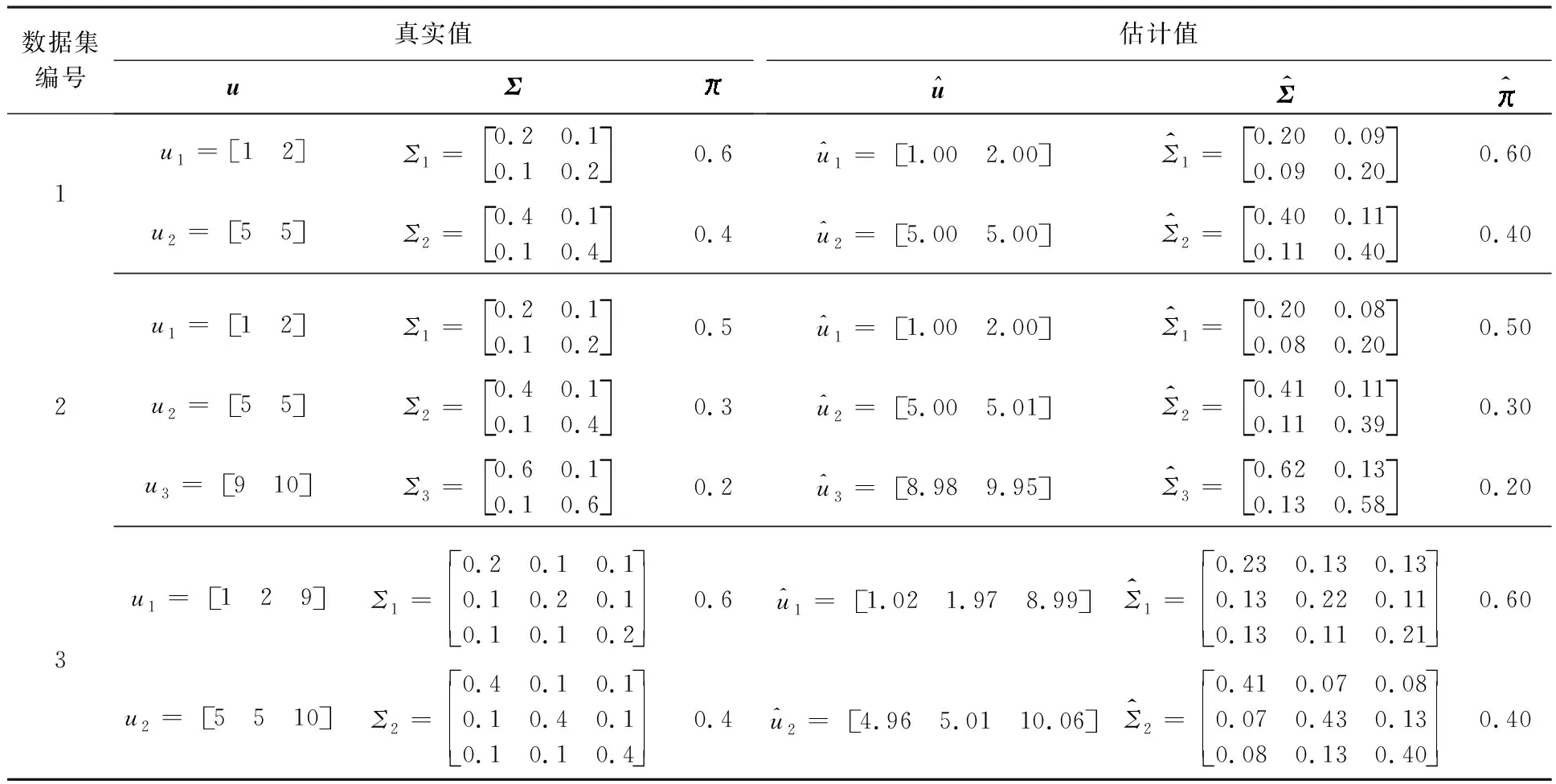
表1 变分贝叶斯算法参数估计结果
从表1可以看出,估计值与真实值之间误差较少,本文算法可以准确估计模型参数以及相应的模型分量数。
在数据集3上,分别采用本文提出的变分贝叶斯算法和EM算法进行计算。不同初始分量数下,EM算法和变分贝叶斯算法收敛时的分量数如表2所示。从表2可以看出,在初始分量数偏离真实分量数时,EM算法估计结果出现很大的偏差,而变分贝叶斯算法则不受初始分量数的影响。

表2 不同算法收敛时的分量数
根据表2可知,在初始分量数为2的条件下,EM算法收敛至真实分量数,因此将EM初始分量数设置为2进行参数估计,其参数估计结果如表3所示。从表3的参数估计结果可以看出,2种算法的估计结果偏差不大,但在相同的数据集下,变分贝叶斯算法的收敛速度远远大于EM算法。
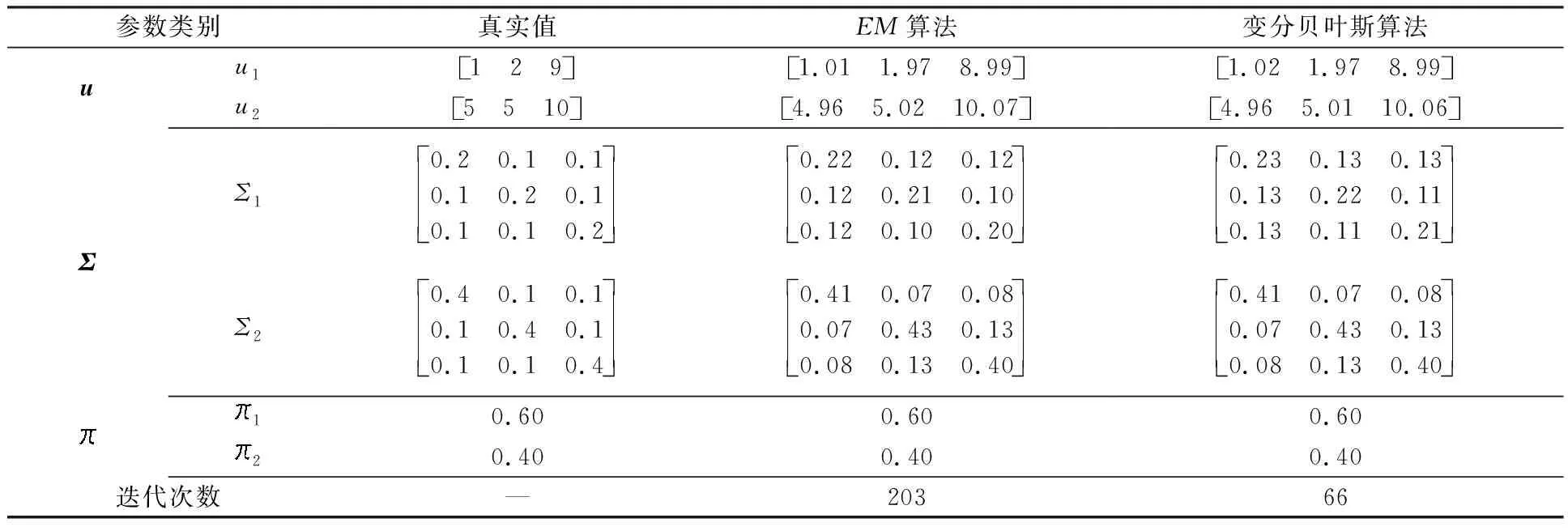
表3 不同算法的参数估计结果
3 实证分析
为验证本文提出的变分贝叶斯算法的效果和性能,运用无限高斯混合模型对Iris(鸢尾花)数据进行拟合。Iris数据集包含150个样本点,3个类别,样本点的个数分别为45,45,60,混合比例为0.30,0.30,0.40,其中每个样本有4种不同的属性。设置初始K值为15,先验分布的参数设置与第2节中数值模拟实验相同。实验结果如表4所示。

表4 Iris数据集模型拟合结果
从表4可以看出,设置远超于真实分量数的初始分量数并不影响算法最后的分量数收敛情况,最后生成3个4维的高斯混合分布与真实数据类别相同。根据估计结来看,无限高斯混合模型的分类准确率达到了90%。
4 结束语
传统高斯混合模型在应用中无法准确估计分量数导致高斯混合模型不能完全、准确、有效地描述这些复杂数据。为此,本文将狄利克雷过程的截棍构造方法与传统有限高斯混合模型结合起来,提出一种拥有无限分量的高斯混合模型。并在变分贝叶斯的理论框架下,展示无限多元高斯混合模型详细的变分推导过程,给出相应的参数估计算法。相比传统的EM算法,本文的变分贝叶斯算法不受初始分量数的影响,在收敛速度上有较大的提升。后续将重点研究基于狄利克雷过程高斯混合模型的在线文本分类问题。
