基于人工鱼群算法的PMSM参数辨识
2021-09-29陶丁兴王家军
陶丁兴,王家军
(杭州电子科技大学自动化学院,浙江 杭州 310018)
0 引 言
永磁同步电动机(Permanent-Magnet Synchronous Motor,PMSM)具有功率密度高、动态性能好、转速运行范围宽等优势,广泛应用于工业伺服驱动系统、电动汽车和高铁等领域[1-2]。目前,PMSM的控制方法主要有矢量控制和直接转矩控制,通过准确获取PMSM的定子电阻、交直轴电感和永磁磁链等参数来提高其控制性能。造成电机实际参数与给定参数之间误差的原因有多种,比如,制造公差导致同一批次生产的电机参数不完全相同;高性能控制驱动器设计者无法获得准确的电机参数,致使控制效果差;电机参数受运行条件和周围环境的影响,产生非线性变化等[3]。为了降低电机参数对控制系统性能的影响,需要对电机参数进行精确辨识。目前,主要通过最小二乘法[4]、模型参考自适应法[5]、遗传算法(Genetic Algorithm,GA)[6]、粒子群算法(Particle Swarm Optimization,PSO)[7]等方法来提高PMSM参数的辨识精度。最小二乘法收敛速度快,但转速突变时,算法的计算量大,跟踪性能差。模型参考自适应法需要根据辨识的参数手动选择自适应率,在多个参数同时辨识时,自适应率的设计比较繁琐。GA算法能够进行并行操作,容易取得全局最优解,但算法需要编码,且对函数搜索的物理意义不直观。PSO算法运用粒子运动路线与人类决策相似的原理得出最优解,易于理解且收敛速度较快,但最大速度和加权因子不易选取,容易陷入局部最优。人工鱼群算法(Artificial Fish Swarm,AFS)[8]是模拟动物行为的群体智能优化算法,简单易于实现,函数优化能力强,收敛速度快,是很好的全局优化算法。本文运用AFS算法进行PMSM定子电阻、磁链、d轴及q轴电感参数的辨识仿真,进一步提高PMSM的参数辨识精度。
1 永磁同步电动机数学模型
在对PMSM进行数学建模时,忽略磁饱和效应、铁芯涡流、磁滞损耗和高次谐波,且气隙磁场按正弦分布,在d轴、q轴同步旋转坐标系下的PMSM数学模型为:
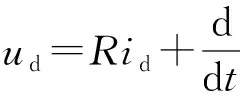
(1)
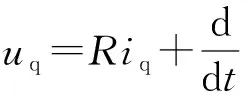
(2)


(3)

(4)

(5)
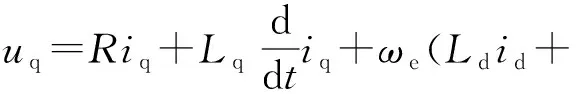
(6)
2 人工鱼群算法
AFS算法是一种基于现实环境中鱼群行为的并行智能优化算法[8]。AFS算法模拟了鱼群的觅食、聚群、追尾和随机行为,通过这些行为找到全局最优值[9]。AFS算法可以有效搜索全局最优值,具有收敛速度快、并行性好、鲁棒性强等优点。
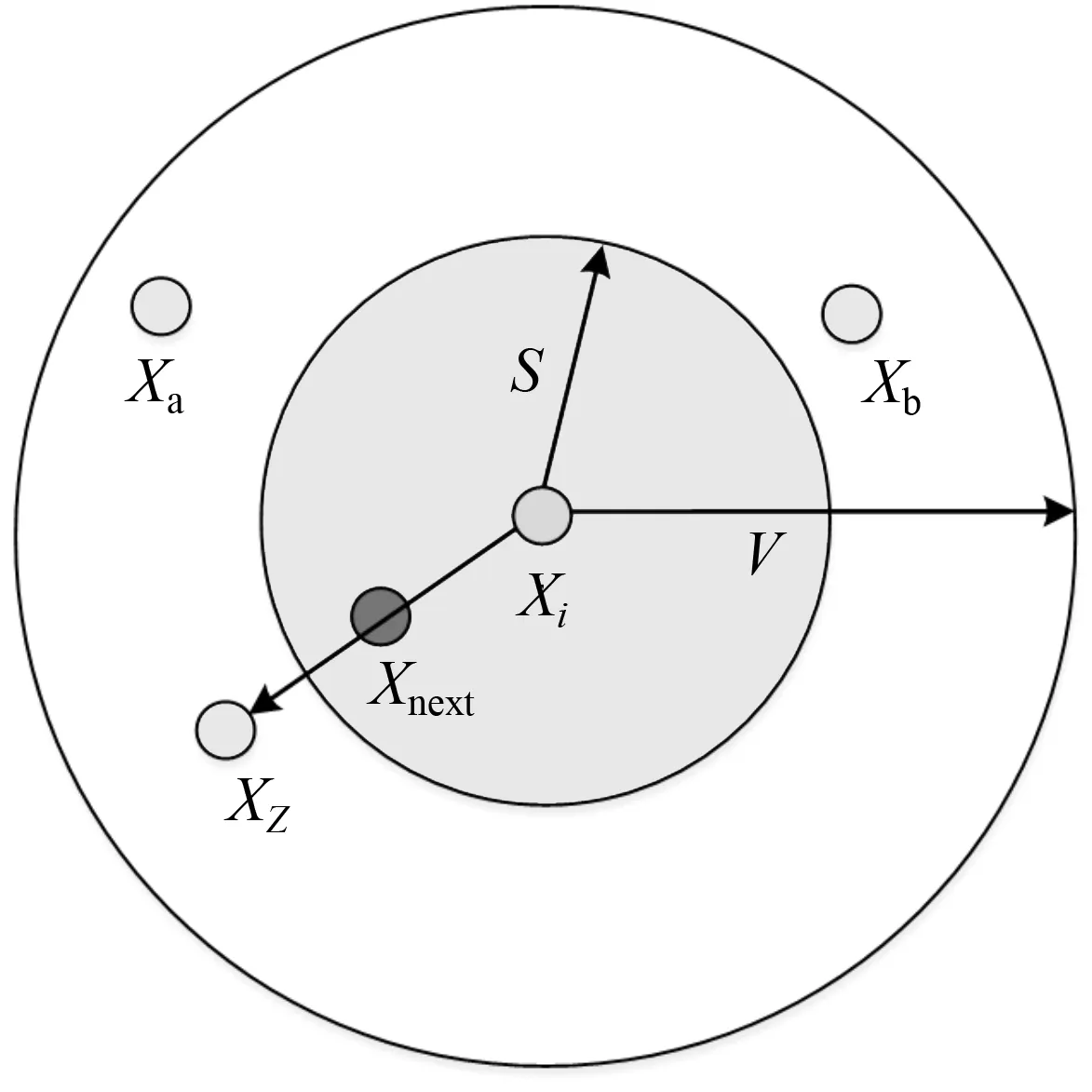
图1 人工鱼视觉概念图
人工鱼视觉概念如图1所示。图1中,Xi为一条人工鱼的当前位置;V为它的视野范围;XZ为其在某时刻的视点所在位置,若此位置的食物浓度高于当前位置Xi,则该人工鱼移动到Xnext,否则继续巡视视野范围内的其他位置;S为人工鱼的最大移动步长。一条鱼巡视的次数越多,对周围环境的掌控度就越高。
2.1 AFS算法概述
AFS算法的行为函数定义为觅食、聚群、追尾和随机等函数。
觅食行为指动物寻找食物的行为,人工鱼通过视觉和嗅觉感知食物,通过浓度来选择移动的方向。假设当前人工鱼的位置为Xi,在其感知范围内随机选择一个位置Xj,若Xj所在位置的食物浓度Yj大于当前位置食物浓度Yi,人工鱼则向此方向移动,否则重新选择位置,若人工鱼尝试移动N次仍未找到符合要求的位置,则执行随机行为。觅食行为的转移方程为:
(7)
式中,rand表示之间的随机数,Xi|next为当前人工鱼动作后的下一个状态,N为人工鱼觅食行为中最大尝试次数。
聚群行为指鱼类集聚成群来集体觅食并躲避伤害的行为。假设当前人工鱼的位置为Xi,在其视野范围内鱼群的数目为m,鱼群的中心位置为Xc,Yc为中心位置Xc的食物浓度,δ为拥挤度因子。如果Yc/m>δYi,则表明鱼群中心有较多的食物且不拥挤,可以向中心位置Yc移动,相反则执行觅食行为。聚群行为的转移方程为:
(8)
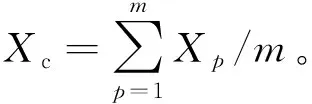
追尾行为指当某一条鱼或几条鱼发现食物时,它们附近的鱼会尾随其后游过来的行为。假设位置Xj人工鱼的食物浓度Yj最高,若Yj/m>δYi,则表明在位置Xj的人工鱼具有较高的食物浓度且不拥挤,当前人工鱼往Xj方向移动;相反则执行觅食行为。追尾行为的转移方程为:
(9)
随机行为指鱼为了在更大范围内寻找食物而随机游动的行为。随机行为是觅食行为的一个缺省行为,在觅食行为尝试M次后,若仍不满足觅食移动条件,人工鱼会在视野范围内随机选择一个位置,然后向该位置移动。随机行为的转移方程为:
Xi|next=Xi+rand×S
(10)
2.2 适应度函数
为了指定AFS算法的优化目标,需要选择适应度函数。可供选择的适应度函数有很多,如时间乘以误差平方积分(Integral of Time-weighted Squared Error,ITSE)、绝对误差积分(Integral of Absolute Error,IAE)和误差平方积分(Integral of Squared Error,ISE)等。IAE和ISE不受时间约束,且不易同时减小超调和调节时间[10]。ITSE既考虑了时间的约束,又能在抑制大偏差的同时缩短调节时间,因此,本文使用ITSE作为永磁同步电动机参数辨识的适应度函数,ITSE的表达式为:

(11)
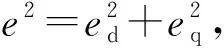
2.3 参数辨识流程

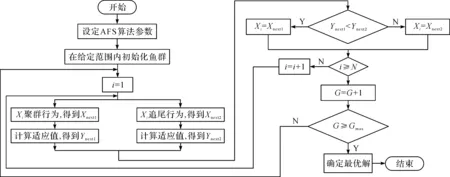
图2 AFS算法流程图
采用AFS算法对永磁同步电机参数进行辨识的主要步骤如下。
(1)设定算法的初始参数。初始参数主要包括鱼群的数量MP、算法的最大迭代次数Gmax、视野范围V、最大移动步长S、拥挤度因子δ和觅食行为中的最大尝试次数N。

x0=(xmax-xmin)×rand(MP,1)+xmin
(12)
式中,xmax和xmin分别为备选解在解空间中的上下限,rand(MP,1)表示在区间上生成MP个随机数。通过式(12)可以在解空间中随机产生第1次迭代所需的备选解x0。
(3)利用备选解进行聚群行为。将第1次初始化的备选解根据式(8)模拟聚群行为,并随机生成第2次的备选解Xnext1。
(4)利用备选解进行追尾行为。将第1次备选解根据式(9)模拟追行为尾,并生成第2次的备选解Xnext2。
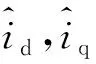
(13)
(6)确定算法的终止指标。本文引入最大迭代次数Gmax作为终止指标,当迭代次数G到达最大迭代次数Gmax时终止。
3 AFS算法辨识原理

辨识原理如图3所示。图3中,AFS算法输入包括d轴、q轴电压ud和uq,d轴、q轴电流id和iq,电角速度ωe,系统实际输入包括ud,uq。
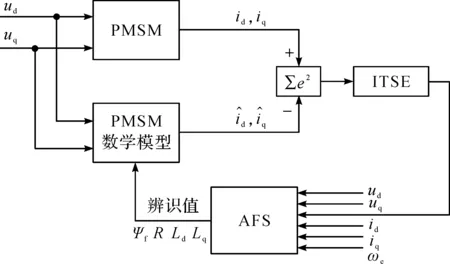
图3 AFS算法辨识算法原理
4 仿真结果与分析
为验证AFS算法辨识PMSM参数的有效性,本文在Matlab/Simulink中搭建了PMSM矢量控制系统,其结构如图4所示,仿真中PMSM的参数如表1所示。
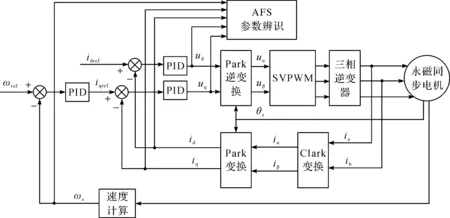
图4 基于矢量控制的ASF算法参数辨识结构图

表1 仿真中PMSM参数



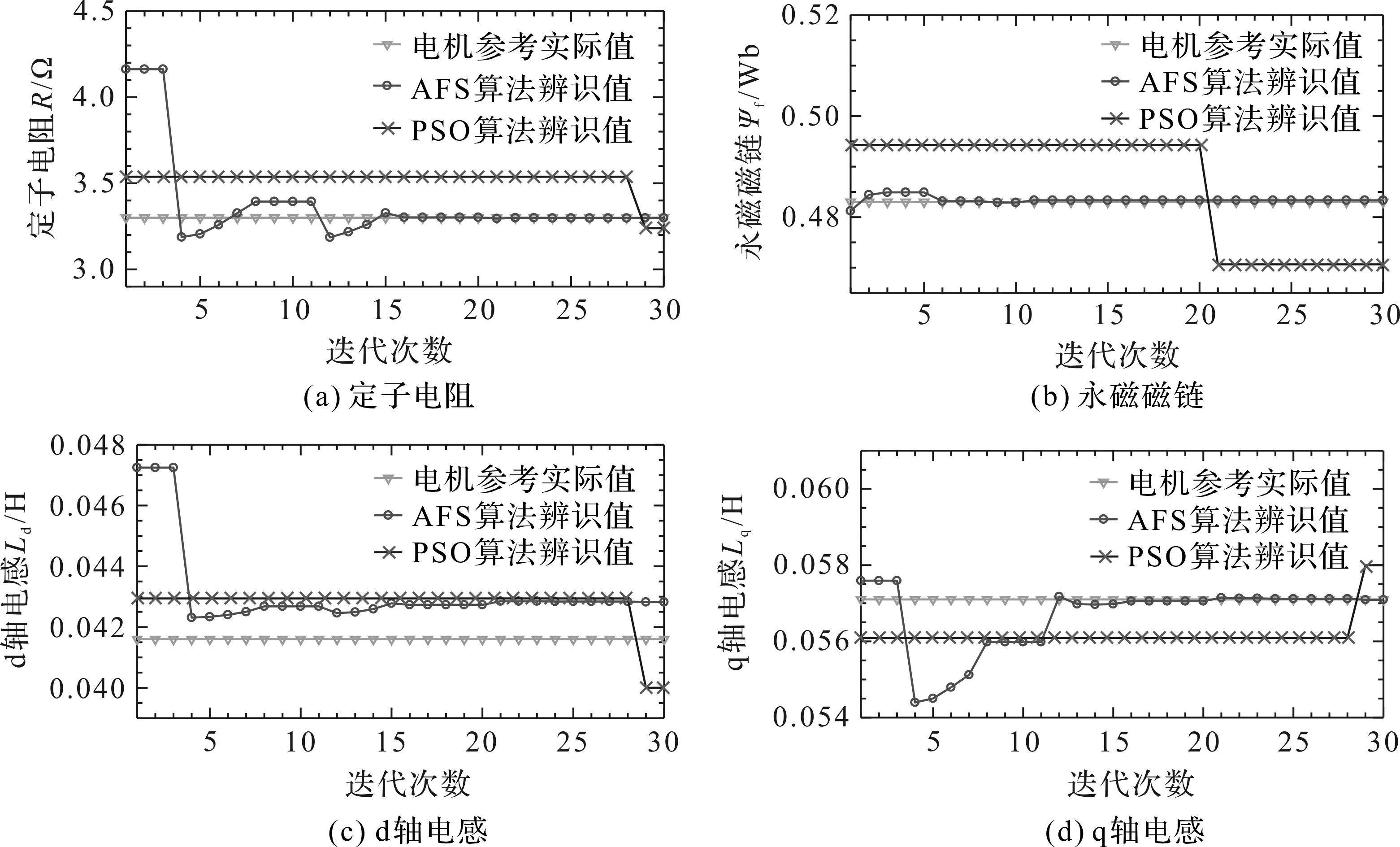
图5 n=600 r/min时,AFS算法与PSO算法的参数辨识结果
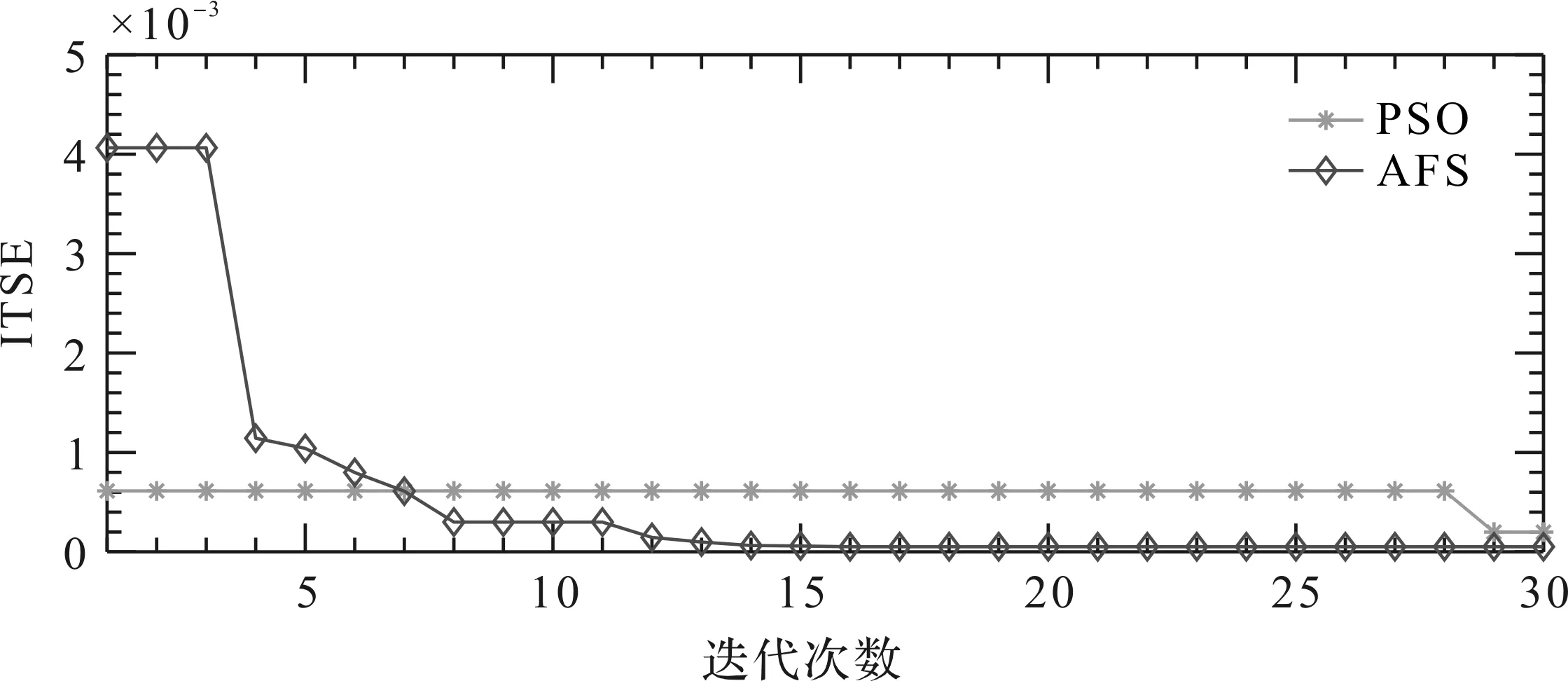
图6 AFS算法与PSO算法适应度函数收敛曲线


图7 正弦信号输入下,AFS算法与PSO算法的参数辨识结果对比

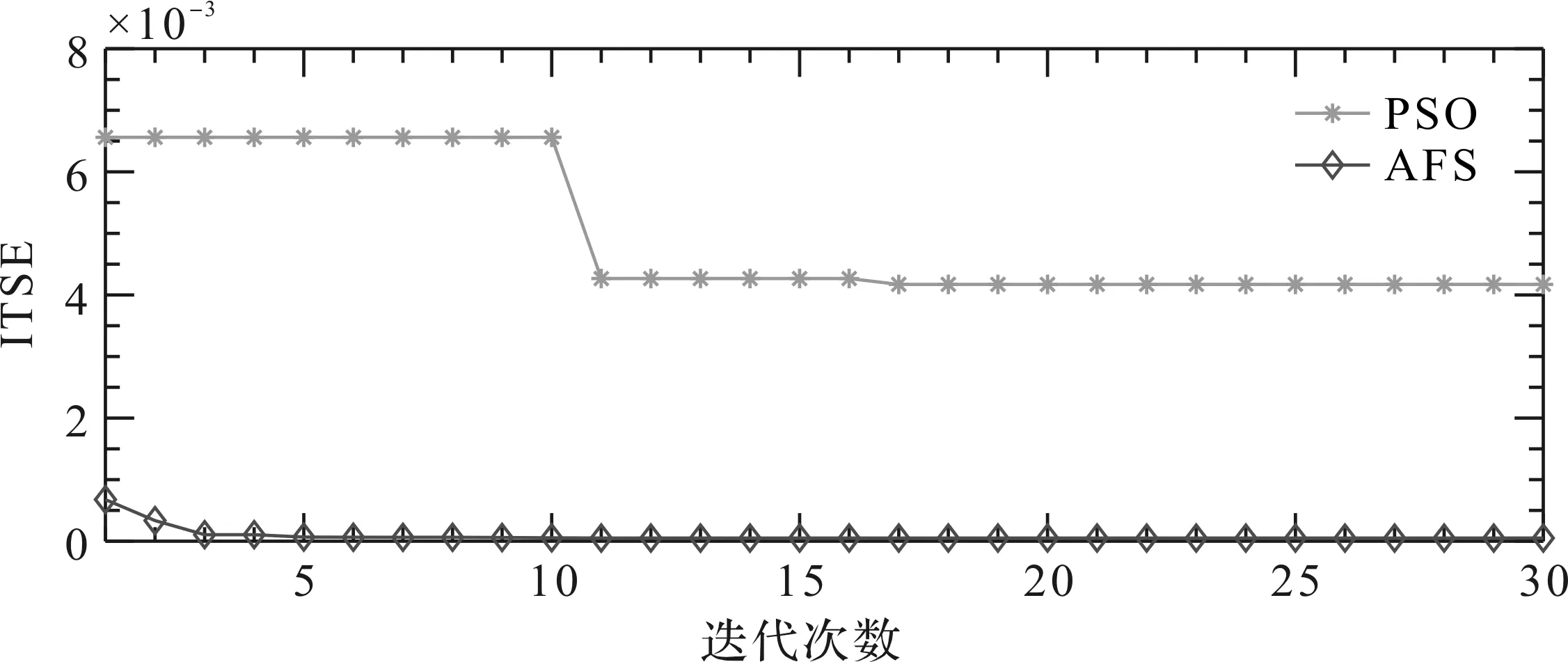
图8 AFS算法与PSO算法适应度函数收敛曲线
为进一步验证AFS算法辨识参数的优越性,转速为阶跃信号和正弦信号的输入条件下,AFS算法与PSO算法辨识的结果及辨识的误差如表2所示。
从表2可以看出,使用PSO算法的参数辨识误差要比使用AFS算法大,在阶跃转速的条件下AFS算法辨识出的参数误差基本与实际值基本相同,误差在0左右;而使用PSO算法辨识出的辨识值与实际值的差距明显增大,误差大都在3%左右。转速为正弦信号时,AFS算法辨识得到的参数与PMSM实际参考值依然基本保持相同;而PSO算法辨识得到的参数与实际值误差进一步加大,误差大约在5%。因此,可明显看出AFS算法的参数辨识精度要高于PSO算法。综合表2和图5、图6、图7和图8可知,与PSO算法相比,AFS算法辨识出的参数误差更小,辨识精度更高,且收敛速度更快。
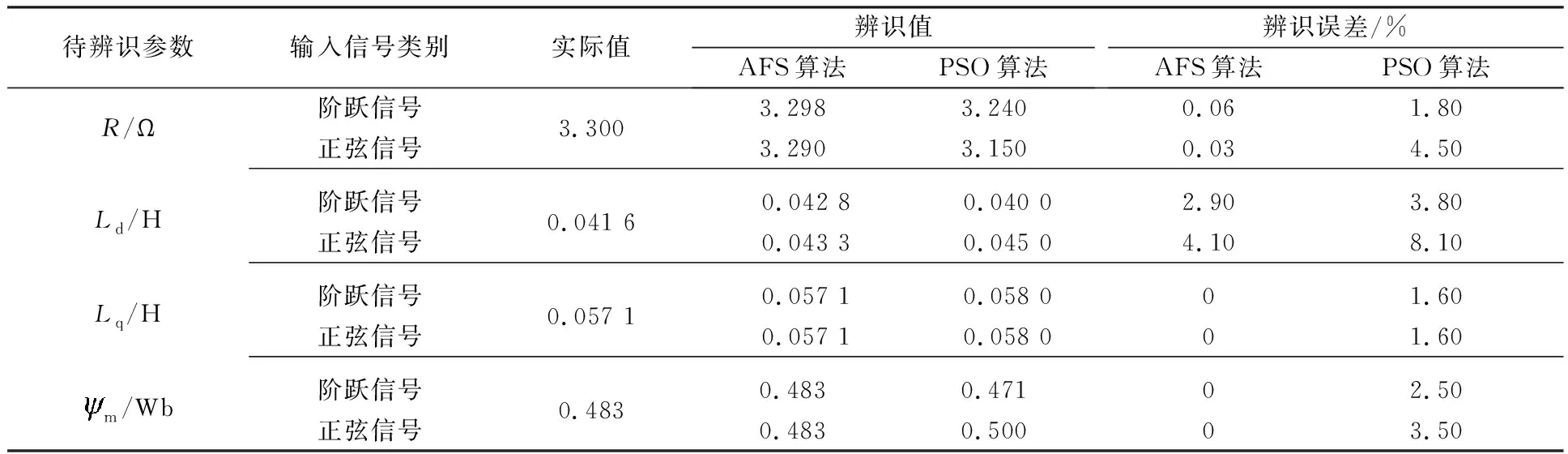
表2 AFS算法与PSO算法辨识结果
5 结束语
为了提高PMSM参数的辨识精度,本文提出一种基于AFS算法的PMSM参数辨识方法。算法实现简单,收敛速度快,辨识精度高。但是,本文是通过离线的AFS算法进行PMSM参数的辨识,后续将针对在线AFS算法的辨识展开进一步研究。
