Possibility to break through limitation of measurement range in dual-wavelength digital holography∗

Tuo Li(李拓),Wen-Xiu Lei(雷文秀),Xin-Kai Sun(孙鑫凯),Jun Dong(董军),Ye Tao(陶冶),and Yi-Shi Shi(史祎诗),†

1School of Electronic Engineering,Xi’an University of Posts&Telecommunications,Xi’an 710121,China

2School of Mathematical Sciences,University of Chinese Academy of Sciences,Beijing 100049,China

3School of Opto-Electronics,University of Chinese Academy of Sciences,Beijing 100049,China

Keywords:digital holography,dual-wavelength interferometry,holographic interferometry

1.Introduction

Beat frequency is a basic phenomenon in nature and is widely used in digital holography.[1–5]In beat frequency digital holography,two wavelengths are usually needed for illumination.Therefore,the beat digital holography is also known as dual-wavelength digital holography(DWDH).[6–10]The DWDH has a large measurement range,so it has aroused the great interest of many researchers in recent years.[11–14]At present,on the one hand,various kinds of DWDH have been proposed to enhance the imaging speed of the DWDH such as deep learning DWDH[15]and single-shot DWDH.[16–20]On the other hand,various noise suppression methods for DWDH have also been proposed to improve the image quality of DWDH,such as linear programming algorithm,[21,22]total variation regularization,[23]additive synthetic-wavelength,[24]and a third illumination wavelength.[25,26]These excellent researches have significantly promoted the development of DWDH.

However,in the DWDH method the beat frequency technique is adopted to integrate two smaller wavelengths into a larger synthetic wavelength.According to the principle of beat frequency,the measurement range of the system should not be greater than one synthetic wavelength.When the height variation of an object is greater than a synthetic wavelength,the DWDH becomes ineffective.[14,15,22]An algorithm is proposed to increase the measurement range to improve DWDH.[27]However,there is no rigorous mathematical proof for why the measurement range can exceed a synthetic wavelength.[27]And the article does not propose how to improve anti-noise performance.Owing to the lack of mathematic support for the algorithm,compared with the conventional DWDH based on beat-frequency,this method has not been widely used.

In this paper,we propose another DWDH method based on constrained undetermined equations.We mathematically prove that the measurement range of this method can exceed a synthetic wavelength.Furthermore,a third wavelength is introduced into the DWDH system,and the corresponding algorithm based on constrained underdetermined equation is designed,which significantly enhances the anti-noise performance of the proposed method.To the best of our knowledge,it is the first time that we have discovered that the DWDH can belong in a problem of underdetermined equations,and it is also the first time that we have strictly mathematically proven that the measurement range of the equivalent wavelength can be exceeded.

Compared with conventional DWDH,it has two advantages:(i)the measurement range is not related toλ1orλ2anymore,which provides convenience for laser selection,and(ii)the measurement range can be larger than the synthetic wavelength.For example,in this study,the two working wavelengths are 532 nm and 632 nm and thus the corresponding synthetic wavelength is 4.34µm.However,we achieve a measurement range of 30µm by using the proposed DWDH.

2.Principle review of the conventional DWDH

Figure 1 shows the scheme of the DWDH.In the DWDH two wavelengths lasers(λ1andλ2)are used as an illumination source,in which a longer synthetic-wavelength is introduced and expressed as follows:

Equation(1)show that the smaller the difference between λ1andλ2,the larger the synthetic wavelengthΛis.And the phase of measured sample can be calculated from

The corresponding height variation of the sample is

If the height variation of the object is less than the synthetic wavelength,the true phase distribution of the object can be acquired by DWI method.But if the surface thickness of the object is greater than the synthetic wavelength,the DWI method does not hold true anymore due to exceeding the measurement range.

3.Principle of proposed DWDH method

We transform the problem of DWDH into a question of constrained undetermined equation.The content of proposed method can be divided into three parts:i)construct a constrained undetermined equation,ii)demonstrate that the constrained undetermined equation has a unique solution,iii)design a searching algorithm to find the unique solution and the height variation of the specimen,and iv)design another corresponding algorithm to enhance the anti-noise performance of DWDH by introducing a third wavelength.

3.1.Constructing constrained undetermined equation

The constrained undetermined equation is constructed here.According to Fig.1,when the laser passes through the specimen,there is

in whichΦλ1andΦλ2are the two unwrapped phases to be obtained;nλ1and nλ2are the refractive index corresponding toλ1andλ2,respectively;h is the height variation of the specimen,mλ1and mλ2are two integers to be obtained;φλ1and φλ1are the two wrapped phases,respectively,which is distributed in[0,2π].

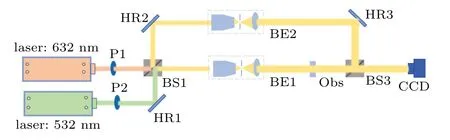
Fig.1.Schematic diagram of dual-wavelength digital holography.

Note that the difference between nλ1and nλ2is neglected in conventional DWDH.In the proposed DWDH,the difference between nλ1and nλ2is considered for the sake of accuracy.For the convenience of mathematical analysis,equation(4)is written as

In the DWDH,it is often considered that the refractive index is known.Andφλ1andφλ1are also known which can be acquired from the interferograms.Thus,in Eq.(5),there are three unknowns(h,mλ1,and mλ2)and two equations.Equation(5)is an undetermined equation which should have infinite solutions.However,since mλ1and mλ2must be integers,equation(5)is a constrained undetermined equation.

3.2.Unique solution demonstration of constrained undetermined equation

We have demonstrated that the equation(5)has a unique solution.And the process of demonstration is given in the following:

Inserting the first equation into the second equation in Eq.(5),one can obtain

The slope K in Eq.(6)is

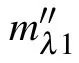
Till now,we have demonstrated that equation(5)has a unique solution in the view of digital holography.Therefore,as long as an algorithm for searching for a unique solution is designed,we can directly find the height variations of the object h.Therefore,in theory,no matter how large h is,we can obtain h by searching for the unique solution of the constrained underdetermined Eq.(5).

3.3.Algorithm to search for unique solution of constrained undetermined equations

We design two algorithms to search for the unique solution of the constrained undetermined equation.One algorithm is based on the system of DWDH.The other algorithm is based on the system of three-wavelength digital holography.The algorithm of three-wavelength digital holography has higher anti-noise performance than the algorithm of DWDH.

Algorithm of DWDHWe design the following algorithm to search for the unique integer solution and the height variation of the specimen.The flowchart of the algorithm is shown in Fig.2.

Fig.2.Flowchart of DWDH algorithm.

The height variation of the object is h(pΔx,qΔy),where p=1,2,...,P,q=1,2,...,Q.The initial value of the vector X(i)(i=1,2...,N)is a zero vector(N can be selected based on the practical situation).The proposed algorithm is shown as follows.

Step 1:let m1=0 and i=1;

Step 2:substitute the value of m1into Eq.(6)and calculate the value of m2;

Step 3:perform the operation X(i)=m2,i=i+1,m1=m1+1;

Step 4:repeat Steps 2 and 3 until i=N,then stop the loop;

Step 5:perform the function transformation Y(pΔx,qΔy)=f{X−rount(X)}which contains the two following operations:where round(·)represents rounding off,min(·)represents taking minimum value of a vector,s represents the coordinate of the minimum value in a vector;

Step 6:perform the operation p=p+1;

Step 7:repeat Steps 2–7 until p=P,and stop the loop;

Step 8:perform the operation q=q+1;

Step 9:repeat Steps 2–9 until q=Q,and stop the loop;

Step 10:perform the operation

whereΦ(pΔx,qΔy)is the unwrapped phase ofφλ2;

Step 11:according to Eq.(4),the height variation of the object is

Till now,the height variation of object is obtained and the measurement process is finished.

Algorithm of three-wavelength digital holographyWe also design the algorithm of three-wavelength digital holography.Compared with the algorithm of DWDH,the algorithm of three-wavelength digital holography enhances the anti-noise performance of DWDH.The schematic diagram of the three-wavelength digital holography is shown in Fig.3.And the flowchart of the algorithm of the three-wavelength digital holography is illustrated in Fig.4.

Fig.3.Schematic diagram of three-wavelength digital holography.

The height variation of the object is h(pΔx,qΔy),where p=1,2,...,P,q=1,2,...,Q.The initial value of X1(i)and X2(i)(i=0,1,2...,N)are all set to be zero vectors(N can be selected based on the practical situation).The proposed algorithm is shown as follows.

Construct the following constrained undetermined equations:

Step 1:let m1=0 and i=1;

Step 2:perform the operation

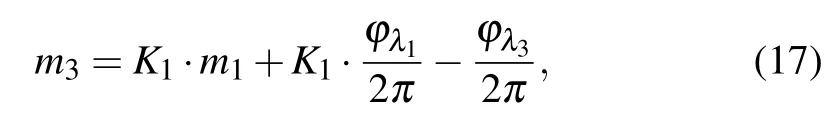
where K1=nλ3λ1/nλ1λ3;

Step 3:perform the operation X1(i)=m2,i=i+1,m1=m1+1;

Step 4:repeat Steps 2 and 3 until i=N,then stop the loop;

Step 5:perform the function transformation Y1=f1{|X1−rount(X1)|}which contains the two following operations:

where round(·)represents the rounding off,fivemin{·}refers to the search for the five smallest values of a vector,and[s1,s2,s3,s4,s5]denotes the coordinates of the smallest five values in the vector;

Step 6:m1=0,i=1,and b=5;

Step 7:perform the operation

where K2=nλ3λ2/nλ2λ3;

Step 8:perform the operation X2(i)=m3,replace i by i+1,and m2by m2+1;

Step 9:repeat Steps 7 and 8 until i=N,then stop the loop;

Step 10:perform the function transformation Y2=f2{|X2−round(X2)|}which represents the two following operations:

Step 11:perform the operation

where fivejiao{·}represents the search for the intersection element of two vectors;

Step 12:perform the operation p=p+1;

Step 13:repeat the Steps 2–12 until p=P,and stop the loop.

Step 14:perform the operation q=q+1;

Step 15:repeat the Steps 2–14 until q=Q,and stop the loop;

Step 16:perform the following operation:

whereΦ(pΔx,qΔy)is the unwrapped phase;

Step 17:According to Eq.(4),the height variation of the object is

Till now,the height variation of object is obtained and the measurement process is finished.

Fig.4.Flowchart of algorithm of three-wavelength digital holography.

4.Results and analysis

Before verifying the proposed method,we make the some statements below.

Whether the off-axis or in-line DWDH system is used,the reconstruction process of conventional DWDH is divided into two steps:.[13–16](I)two wrapped phase maps(φλ1and φλ2)are retrieved from the interferograms,and(II)by using the beat frequency technique,the two wrapped phase maps are integrated into an unwrapped phase map.

The reconstruction process of the proposed DWDH is also divided into two steps:I)retrieve the wrapped phase maps from the interferograms,and II)by using the constrained undetermined equation,the two wrapped phase maps are integrated into an unwrapped phase map.

A comparison between the conventional DWDH and the proposed DWDH shows that their first steps are the same,but their second steps are different.Therefore,for simplicity in the following tests,we omit the first step of the proposed method(on the assumption thatφλ1andφλ2are both known)and perform the demonstration starting from the second step directly.

4.1.Results obtained by using dual-wavelength algorithm

Two working wavelengths applied are chosen as 474 nm and 532 nm,respectively.Thus,the synthetic wavelength is 4.34µm.Two specimens are tested.One specimen is an inclined plane,the other specimen is a specimen with large discontinuity.And the maximum height variations of the two specimens are both set to be 30µm,which exceeds the synthetic wavelength.

Figure 5(a)shows the original height map of the inclined plane.The two corresponding wrapped phase maps(φλ1and φλ2)of the inclined plane are illustrated in Figs.5(b)and 5(c),respectively,which are both distributed in[0,2π].Figure 5(d)shows the retrieved height map of the incline plane by using the proposed algorithm of DWDH.A comparison between Fig.5(c)and Fig.5(d)indicates that the retrieved height map is nearly the same as the original height map.

To further demonstrate the validity of the DWDH algorithm,we test the specimen with high discontinuity which is shown in Fig.5(e).The two wrapped phase maps of the specimen are illustrated Figs.5(f)and 5(g),respectively,which are both distributed in[0,2π].Figure 5(h)shows the retrieved height map by using the proposed algorithm of DWDH.Comparing Fig.5(e)with Fig.5(h),the retrieved height map is found to be nearly the same as the original height map.

These results demonstrate that the proposed algorithm of DWDH is effective.

Fig.5.Results obtained by using dual-wavelength algorithm,showing(a)height map of inclined plane,((b),(c))wrapped phase maps of 474 nm and 532 nm which are distributed in[0,2π],(d)retrieved height map of inclined plane,(e)height map of another specimen with large discontinuity,((f)–(g))wrapped phase map of 474 nm and 532 nm which are distributed in[0,2π],and(h)retrieved height map of another specimen with large discontinuity.

4.2.Results obtained by three-wavelength digital holography

Three working wavelengths are chosen as 474 nm,532 nm,and 632 nm,respectively.Thus,the maximum synthetic wavelength is 4.34µm.Two different specimens are tested here.One specimen is a Gaussian plane,and the other specimen is a specimen with large height discontinuity.And the maximum height variations of the both the specimens are set to be 30µm,which exceeds the measurement range of DWDH based on beat frequency.

Figure 6(a)shows the original height map of Gaussian plane.The three wrapped phase maps(φλ1,φλ2,andφλ3)of the Gaussian plane are illustrated Figs.6(c)–6(e),respectively,which are all distributed in[0,2π].Figure 6(i)shows the retrieved results of the incline plane.Comparing Fig.6(a)with Fig.6(i),we can see that the retrieved height map is nearly the same as the original height map.

To further demonstrate the validity of the method,we choose the specimen with high discontinuity as shown in Fig.6(b).The three wrapped phase maps of the specimen are illustrated Figs.6(f)–6(h),respectively,which are all distributed in[0,2π].Figure 6(j)shows the retrieved results by using the proposed algorithm of three-wavelength digital holography.A comparison between Fig.6(b)and Fig.6(j)shows that the retrieved height map is nearly the same as the original height map.

These results demonstrate that the three-wavelength algorithm is effective.

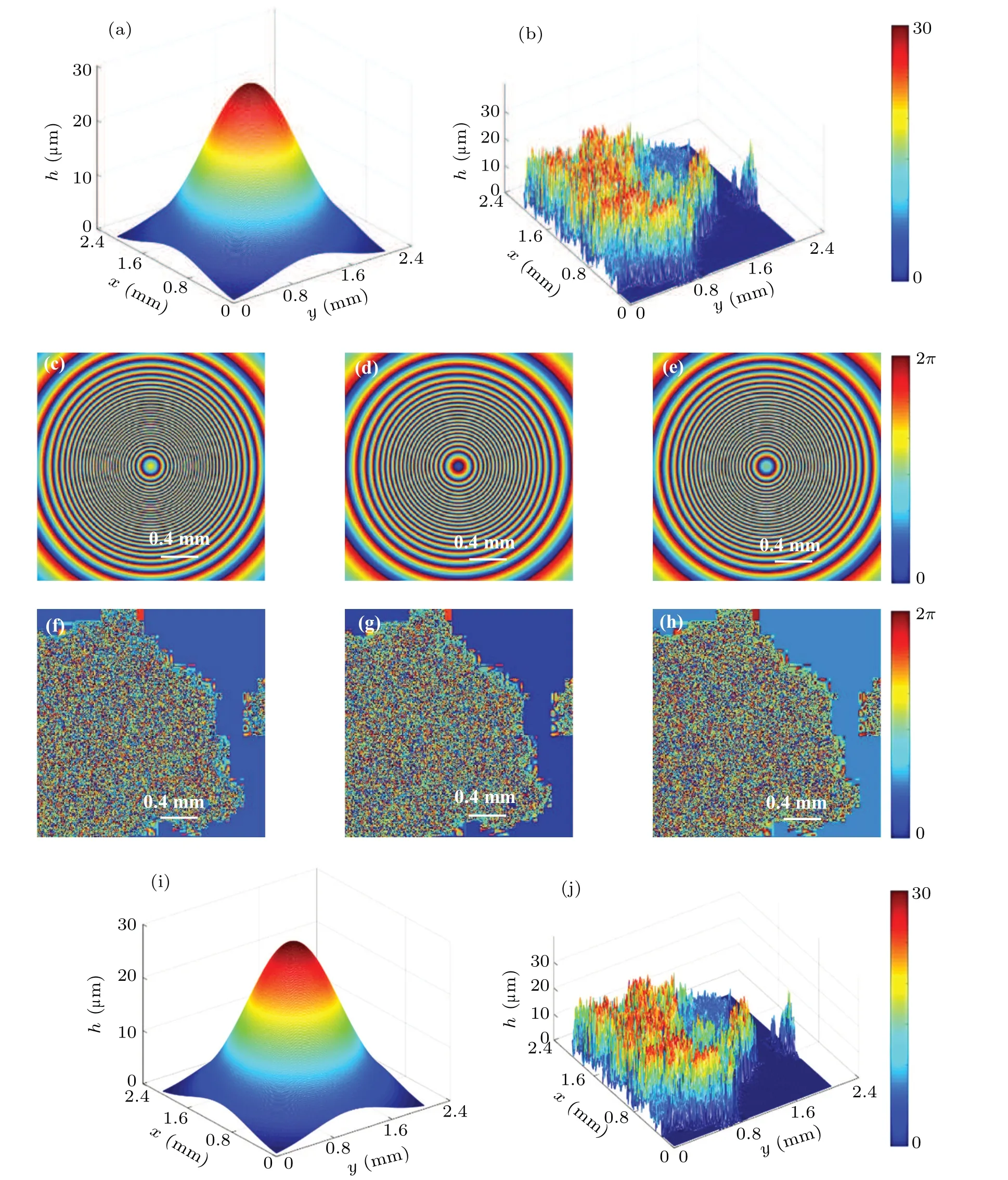
Fig.6.Results obtained by using three-wavelength algorithm,showing(a)height map of Gaussian plane:((c)–(e))wrapped phase maps of 474 nm,532 nm,and 632.8 nm which are distributed in[0,2π],(i)retrieved height map of Gaussian plane;(b)height map of another specimen with large discontinuity,((f)–(h))wrapped phase maps of 474 nm,532 nm,and 632.8 nm which are distributed in[0,2π],and(j)retrieved height map of another specimen with large discontinuity.

4.3.Comparison and analysis

We compare the anti-noise performance of dualwavelength algorithm with the anti-noise performance of three-wavelength algorithm.

Anti-noise performance of dual-wavelength algorithm

We test the anti-noise performance of the dual-wavelength algorithm.As the wrapped phases(φλ1andφλ2)may be contaminated by the noise in a practical case,the algorithm of dual-wavelength is tested in the noise contaminated condition.Assume that the wrapped phases(φλ1andφλ2)are both contaminated by random noise.The random noise is generated by({Mean[|φ|]}/SNR)∗V,where Mean denotes a mean value of the wrapped phase,V is a two-dimensional(2D)variable randomly distributed in a range of[−0.5,0.5],and SNR represents the signal-to-noise ratio.[28]Figures 7(a)–7(f)show the reconstructed results whenφλ1andφλ2are contaminated by noise to different degrees(SNR=120,110,100,60,50,and 40),respectively.These results show that for slight noise,the negative effect for reconstruction is legible.As random noise increases,the fidelity of reconstructed result is degraded.This problem can be solved by the noise suppression methods of DWDH.[21–26]Further,based on the undetermined equations method,we develop the three-wavelength algorithm to solve the noise problem.

Fig.7.Retrieved height maps of the inclined plane in the case thatφλ1 andφλ2 are contaminated by noise,indicating:(a)–(f)unwrapped results obtained by using dual-wavelength algorithm whenφλ1 andφλ2 are contaminated with random noise to different degrees(SNR=120,110,100,60,50,40)respectively.

Anti-noise performance of three-wavelength algorithmWe test the anti-noise performance of the threewavelength algorithm.As the wrapped phases(φλ1,φλ2,and φλ3)may be contaminated by the noise in a practical case,the three-wavelength digital holography is tested in the noise contaminated condition.Assume that the wrapped phases(φλ1,φλ2,andφλ3)are all contaminated by random noise.[28]Figures 8(a)–8(f)are the results whenφλ1,φλ2,andφλ3are contaminated by noise to different degrees(SNR=120,110,100,60,50,and 40),respectively.A comparison between Figs.7 and 8 shows that the three-wavelength algorithm is more robust than the dual-wavelength algorithm.Note that although the three-wavelength algorithm has higher anti-noise performance than the algorithm of DWDH,the system of threewavelength digital holography is more complex than the system of DWDH.Therefore,whether the method of DWDH or the method of three-wavelength digital holography is chosen,one should follow the actual situations.

Fig.8.Retrieved height maps of inclined plane in the case thatφλ1,φλ2,andφλ3 are contaminated by noise,obtained from((a)–(f))unwrapped results by using three-wavelength algorithm when theφλ1,φλ2,andφλ3 are contaminated with random noise to different degrees(SNR=120,110,100,60,50,40)respectively.

Finally,we analyze the noise and accuracy of DWDH.Owing to the use of beat frequency principle,the problem of noise synchronous amplification is inherent in the conventional DWDH.Now,the relative noise is assumed to beεm=2%(m=1,2).The optical path error of single-wavelength is λmεm,and the optical path error of the synthetic wavelength is 2Λεm.If the recording wavelengthλmis equal to 600 nm,we can calculate the optical path error of single-wavelength and the optical path error of synthetic wavelength to be 12 nm and 160 nm,respectively.The optical path error of synthetic wavelength is about 13 times larger than the optical path error of single wavelength.This is the noise amplification problem of DWDH.It is worth pointing out that the proposed method based on underdetermined equations does not use the synthetic wavelength and thus it does not experience the abovementioned noise amplification process.Therefore,this method has stronger anti-noise performance and higher accuracy theoretically.

5.Conclusions and perspectives

In this work,we proposed a DWDH method which is based on undetermined equations.To the best of our knowledge,it is the first time to show the thermical possibility of breaking the measurement range of the DWDH method.Further,a third wavelength is introduced into the DWDH method and a corresponding algorithm is designed,which enhances the anti-noise performance of the proposed DWDH method.A series of simulations is obtained to demonstrate the effectiveness of the proposed method.More importantly,since the principle of proposed DWDH method is based on basic mathematical principles,it can be further extended to the various fields,such as dual-wavelength microwave imaging and dualwavelength coherent diffraction imaging.This research may provide a good tool for the DWDH to break the measurement range in conventional DWDH method.

Acknowledgment

The authors thank Qian Zhang,Dongyu Yang,and Jin Wen for their useful discussion.