镍基高温合金中γ″和δ相的热力学性质与相变判定*

2021-09-28孙昊昉田素贵刘丽荣

沈阳工业大学学报 2021年5期

孙昊昉，田素贵，刘丽荣，金莹

(1.沈阳工业大学材料科学与工程学院，沈阳 110870；2.沈阳化工大学能源与动力工程学院，沈阳 110142)

γ″相是以GH4169为代表的镍基多晶高温合金中的一种重要强化相，热处理后约占合金体积分数的15%，其强化效果来自γ″相与基体γ相之间的共格应变[1].δ相可在合金的晶界或晶内析出，在晶内析出主要为γ″→δ相变过程，δ相的析出形态与热处理或服役温度有关[2].

γ″和δ相的成分均为Ni3Nb，惯用晶胞均含有6个Ni原子和2个Nb原子，其中γ″相是亚稳态，δ相是γ″相的稳定相.当合金处于650 ℃及更高温度的长期服役条件下时，作为GH4169合金主要强化相的γ″相会粗化并转化为δ相[1-2]，因而δ相为γ″→δ相变过程的高温相.由于相变后γ″强化相数目减少，因而导致合金力学性能降低[3].相关研究[4]证实在冷轧加工过程中，外力会导致GH4169合金中的δ相加速析出.在合金的时效热处理阶段，大量γ″相转变为δ相[5]；热锻过程中的高温变形也会加速GH4169合金中γ″和δ相的析出[6].因此，可以推测γ″→δ相变过程是由应力或温度诱发的.由于合金中γ″和δ相的析出数量与形貌会对合金的力学性能产生重要影响，因此，有必要对γ″和δ相的相变规律、影响因素等方面展开研究，相应结论可作为合金成分设计、工艺优化的依据.

对成分相同、结构不同的γ″和δ相采用第一性原理进行相变模拟，以两相的能量-体积关系曲线为理论基础，分析两相的相变情况及相关热力学性质[7].对镍基高温合金中的常见析出相，已经开展了较多的有关相变和热力学性质等方面的研究，近年来Lin等[8-9]对γ″和δ相的热力学性质开展了相关研究，但目前有关γ″和δ相相变方面的研究尚不多见.本文以GH4169合金中的γ″和δ相为研究对象，通过获取其在不同压强条件下的能量-体积关系曲线，计算两相相关热力学性质参数并分析其相变情况.

1 模型建立与计算方法

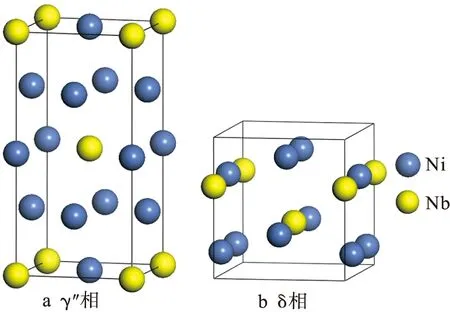
图1 γ″相和δ相的晶体结构Fig.1 Crystal structures of γ″ and δ phases

为了获取上述两相晶体结构的能量-体积关系，本文在第一性原理计算中采用施加不同静水压的方式获取了两相晶体的平衡体积，并计算该体积对应的总能量.在上述计算过程中利用CASTEP软件进行结构优化并计算体系的总能量及相关性质.结构优化采用的计算参数要求为：单个原子体系总能量小于2.0×10-6eV，最大应力偏差为0.02 GPa，每个原子上的作用力小于1 eV/nm，最大原子位移不超过0.5×10-4nm；采用MP方法设置简约布里渊区内的k点；计算体系总能量选用的收敛值为1.0×10-6eV，截断能设置为480 eV；所有计算中采用PW91交换关联泛函.

采用Birch-Murnaghan状态方程方法，将计算得到的能量-体积关系曲线拟合为两相的状态方程，即E(V)方程；选用附带热效应的准谐德拜模型，并结合上述状态方程可计算得到吉布斯自由能表达式；利用麦克斯韦关系式和其他关系式得到两相的其他热力学参数.可采用Gibbs2或EosFit7等开源计算软件[10]完成上述计算过程.

可根据化学势μ在相变前后的变化情况，将相变分为一级相变与二级相变[11].无论一级相变还是二级相变，化学势均保持不变；一级相变时，化学势对压强p或温度T的一阶偏导发生跃变；二级相变时，化学势对压强p或温度T的一阶偏导保持不变，但二阶偏导发生跃变.化学势与吉布斯自由能关系密切，在单一组元体系中化学势等于吉布斯自由能，在多组元体系中化学势等于偏摩尔吉布斯自由能[12].在相变判断中化学势对压强与温度的一阶偏导具有热力学意义，具体表达式如式(1)和(2)所示，其中S为熵，V为体积.化学势的二阶偏导也具有物理意义，具体表达式如式(3)～(5)所示，其中，β为压缩系数；Cp为定压热容；α为线膨胀系数.可以通过计算上述热力学参数来判断相变性质.

(1)

(2)

(3)

(4)

(5)

2 计算结果与分析

2.1 能量-体积关系

以γ″和δ相的惯用晶胞为计算对象，对其在-25～1 200 GPa静水压条件下进行几何优化并计算模型的总能量，得到两相在不同压强条件下的晶格结构、晶格常数、体积和总能量，两相能量-体积关系如图2所示.由于在自然条件下体系的总能量趋于最小，因而图2中两条曲线的最低点表示在基态条件下两相的平衡体积和总能量，其中γ″相平衡体积约为0.099 860 2 nm3，晶格常数a=b=0.364 83 nm，c=0.750 26 nm，总能量约为-11 248.402 68 eV，与晶格常数的实际测量值[13](0.362 4 nm、0.740 6 nm)的误差在1.5%以内；δ相平衡体积约为0.099 763 2 nm3，晶格常数a=0.512 91 nm，b=0.426 49 nm，c=0.456 06 nm，总能量约为-11 248.451 35 eV，与晶格常数的实际测量值[13](0.511 0 nm、0.425 0 nm、0.454 0 nm)的误差在0.5%以内，上述结果说明本文第一性原理的计算参数选择合理，计算结果可靠.由图2a可见，两相的能量-体积关系曲线高度接近.由图2b可见，两相的总能量差值为正，说明γ″相的能量一直高于δ相.上述现象表明两相之间存在如下相变关系：能量较高的γ″相为亚稳态，能量较低的δ相为稳态；由于自然界中体系总是趋向于能量最小的状态，因而相变方向为γ″→δ，符合前述实验结果.观察图2b可以发现，两相最大能量差不超过0.12 eV，即能量差约为体系总能量值的十万分之一，这属于非常微小的能量差.由于图2b中两相能量差大于零，表明两相的能量-体积关系曲线不相交，因而无法应用常见的等压公切线方法判定相变[7].由图2可知，成分相同、结构不同的γ″和δ相具有高度接近且不相交的能量-体积关系曲线.

图2 γ″相和δ相的能量-体积关系曲线Fig.2 Energy-volume relationship curves of γ″ and δ phases

2.2 吉布斯自由能

通过Gibbs2软件可计算出吉布斯自由能，而吉布斯自由能可以反映化学势的变化.在300 K下γ″相和δ相的吉布斯自由能与压强的关系如图3所示.由图3a可见，随着压强的增加，两相的吉布斯自由能呈上升趋势且两相的吉布斯自由能十分接近.由图3b可见，γ″相的吉布斯自由能高于δ相，且其差值会随压强的增加而变大，当压强接近200 GPa时，吉布斯自由能差值趋于稳定.两相自由能的差值小于体系自由能值的十万分之一，表明如果在上述压强区间内发生相变，体系相变前后的吉布斯自由能可保持相对稳定.

图3 γ″相和δ相的吉布斯自由能与压强的关系Fig.3 Relationship between Gibbs free energy and pressure of γ″and δ phases

在0 GPa条件下γ″和δ相在0～1 500 K温度范围内的吉布斯自由能与温度的关系如图4所示.由图4a可见，两相的吉布斯自由能随着温度的增加而降低，当温度较高时，吉布斯自由能呈现加速降低的趋势，在0 GPa和不同温度条件下，两相吉布斯自由能的数值十分接近.由图4b可见，两相吉布斯自由能差值随温度的增加而减小，且该差值大致相当于两相吉布斯自由能值的十万分之零点五.如果在上述温度区间内发生了相变，可认为相变前后吉布斯自由能是稳定的.由于在一定范围内可以用吉布斯自由能代替化学势，因此，可认为发生γ″→δ相变时，两相的化学势相等，符合相变特征.

图4 γ″相和δ相的吉布斯自由能与温度的关系Fig.4 Relationship between Gibbs free energy and temperature of γ″ and δ phases

2.3 焓

由于焓和熵密切相关，且在一定范围内可用焓表示熵的变化情况，在第一性原理计算中，除了可用形成热和结合能判断相的稳定性[14]，也可用焓判断相的稳定性，焓越低说明热力学稳定性越高.本文计算了γ″和δ相在0 K条件下焓随压强(0～200 GPa)的变化情况，结果如图5所示.由图5a可见，γ″和δ相的焓随着压强的增加而增加，且增幅逐渐变缓.由图5b可见，γ″和δ相的焓差值随着压强的增加而增加并逐渐趋于稳定.δ相具有较低的焓，说明在上述压强范围内δ相具有较好的稳定性.图5b表明，两相的焓-压强曲线不相交且非常接近，焓差值大致相当于体系焓值的十万分之一.因此，可认为在相变时两相的焓(或熵)保持稳定.结合式(1)可知，相变时化学势对温度的一阶偏导不变，因而γ″→δ相变不是一级相变.

图5 γ″相和δ相的焓与压强的关系Fig.5 Relationship between enthalpy and pressure of γ″ and δ phases

2.4 体积参数

2.4.1 相变体积

由图2可知，γ″和δ相的能量-体积关系曲线高度接近且不相交，这说明在可能的相变点处两相的体积高度接近，即无体积突变发生.据式(2)可知，此时化学势对压强的一阶偏导不变，因而γ″→δ相变非一级相变.

2.4.2 体积压缩率

本文计算了γ″和δ两相在不同压强条件下体积V与0 GPa条件下体积V0的比值，即体积压缩率，结果如图6所示.施加静水压时，两相的体积均会减小，且体积压缩率变小，这说明晶体内部原子间的斥力随着体积的减小而增加，并与外部压力保持平衡.由图6a可见，两相的体积压缩率曲线存在一定差距.由图6b可见，随压强的增加体积压缩率差值也随之增加并逐渐趋于稳定.两相体积压缩率差值较大，约为2‰，可认为γ″→δ相变伴随体积压缩率的突变，结合式(3)可知，化学势的二阶偏导发生突变，因而该相变为二级相变.此外，在不同压强条件下两相热力学性质(体积压缩率)差值曲线的形态与吉布斯自由能差值(图3b)及焓差值(图5b)接近，表明两相的热力学性质差值的变化具有一致性：热力学性质的差值在加压初期快速增加，并随压强的增加而趋于稳定.

图6 γ″和δ相的体积压缩率与压强的关系Fig.6 Relationship between volume compression rate and pressure of γ″ and δ phases

2.4.3 体积膨胀率

本文计算了γ″和δ相在0 GPa条件下体积与温度(0～1 500 K)的关系，由于金属具有热膨胀效应，两相从基态开始随温度增加出现了体积膨胀的现象.本文采用体积膨胀率指标进行分析，得到的γ″和δ相的体积膨胀率与温度的关系如图7所示.由图7a可知，γ″和δ相的体积随温度的增加而膨胀，且随温度的增加，体积膨胀率的增速加快.由7b可见，随温度的增加两相体积膨胀率差值也随之增加，且最大差值约为3.24‰.由于γ″相在受热时膨胀得更大，因此，在上述温度范围内发生γ″→δ相变时，体积膨胀率会明显缩小，结合式(3)可知，化学势的二阶偏导发生突变，因而该相变为二级相变.

图7 γ″和δ相的体积膨胀率与温度的关系Fig.7 Relationship between volume expansion rate and temperature of of γ″ and δ phases

2.5 线膨胀系数

线膨胀系数用于表征材料在温度作用下膨胀或收缩程度的物理量，其数值与材料的晶体结构及成键强度相关，通常成键强度高的材料具有较低的线膨胀系数.由于线膨胀系数与温度的关系密切，因而本文计算了γ″和δ相在不同温度条件下的线膨胀系数.γ″相和δ相的线膨胀系数与温度的关系如图8所示.由图8a可知，两相的线膨胀系数随温度的增加而增加.由于原子具有非谐效应，原子在振动时会引起一定的相互斥力，进而引起热膨胀现象，热膨胀主要是由晶格振动引起的.当温度较高时，随晶体膨胀原子间距的增加，原子间的合力表现为逐渐增加的引力，可抑制晶体的膨胀.由图8a可见，高温区域线膨胀系数曲线趋于平缓，γ″相具有较大的热膨胀效应，这与其体积膨胀率效应一致.由图8b可见，随着温度的增加，两相线膨胀系数的差值变大.由式(5)可知，线膨胀系数可以表示为化学势的二阶偏导形式，同时γ″和δ相的线膨胀系数又有较大的差距，因此，γ″→δ相变会导致化学势的二阶偏导出现跃变，即该相变属于二级相变.

图8 γ″相和δ相的线膨胀系数与温度的关系Fig.8 Relationship between linear expansion coefficient and temperature of γ″ and δ phases

2.6 等压热容

据式(4)可知，等压热容可以表示为化学势的二阶偏导形式，因而可用于判定相变的性质.本文计算了γ″和δ相在不同温度条件下的等压热容与温度的关系，结果如图9所示.从图9a可知，两相的等压热容随温度的增加而增加并逐渐趋于稳定.晶格振动与电子热运动均对热容有贡献，且分别与T3和T成比例关系.在极低温范围内，电子热容因与温度呈线性关系而占主导地位.由于晶格热容与T3成比例关系，随温度的增加晶格热容快速增加并占主导地位，此时可忽略电子热容的作用[15-16]，高温时晶格热容趋于杜隆-珀蒂极限.热容和线膨胀系数均由原子振动引起，体现在图9a与图8a的变化趋势相同，并符合格林艾森定律.当温度变化时，热容近似与热膨胀系数成比例关系.由图9b可见，随着温度的增加，两相的等压热容差先减小后增加，最小热容差约为体系热容的1.5‰，这说明当γ″→δ相变时，化学势的二阶偏导出现跃变，因而该相变属于二级相变.

图9 γ″相和δ相的等压热容与温度的关系Fig.9 Relationship between heat capacity at constant pressure and temperature of γ″ and δ phases

3 讨论

在本文计算结果中以“化学势一阶偏导的热力学性质在两相间的差距小于十万分之一，化学势二阶偏导的热力学性质在两相间的差距大于千分之一”为相变判断依据.而“小于十万分之一”和“大于千分之一”两个范围之间至少相差两个数量级，具有较好的区分度和可操作性.因此，本文采用上述标准判断热力学性质是否发生突变.对γ″→δ二级相变的判别分为三个阶段.首先，根据两相高度接近的吉布斯自由能(化学势)判断该相变具有相变的共性——化学势不变.其次，根据两相高度接近的体积和焓(熵)，说明化学势的一阶偏导在相变时不发生突变，证明该相变不是一级相变.最后，由于两相体积压缩率、体积膨胀率、线膨胀系数及等压热容指标具有较明显差距，表明化学势的二阶偏导在相变时发生突变，据此判断该相变为二级相变.

在所有相变过程中晶体结构的对称性都会发生改变，但一级相变和二级相变在晶体对称性改变方面存在差别.二级相变发生时，通常新旧两个相的晶体结构间存在子群和母群的关系[17]，原因在于当发生二级相变时，发生了原子位置的小幅变化或是原子团的旋转，这种变化仅是部分对称性消失，而其余对称性得到了保留.

以γ″→δ相变中原子的Wyckoff位置为比较对象，γ″相原子的位置为Nb-2a、Ni-2b和Ni-4d，δ相原子的位置为Nb-2a、Ni-2b和Ni-4f.相变前后两相对称性的变化主要表现为体系中的部分Ni原子发生了位移(4d→4f)，其他原子的Wyckoff位置保持不变.因此，从相变前后Wyckoff位置的微小变化可证实γ″→δ相变属于二级相变.

图10 原子数目不变时全部可能的二级相变Fig.10 All possible second-order phase transitions with constant number of atoms

由图10可见，γ″相的D4h群和δ相的D2h群之间存在着不经过其他结构的直接二级相变路径，说明本文提出的γ″→δ相变为二级相变的推断真实有效.据伐因斯坦等[17]的观点可知，多数情况的二级相变过程中，高温相的对称性更高.而GH4169合金在650 ℃以上会出现γ″→δ相变，据协形群的分类方法可知，δ相作为高温相，其对称性更低.因此，本文所研究的γ″→δ相变属于二级相变的一个特例，其低温相的对称性较高.