一种无需预设模板的动车组故障识别算法*
2021-09-28刘子宽
李 超,刘子宽
(中国铁道科学研究院集团有限公司 电子计算技术研究所,北京 100081)
为了满足日益增长的运输需求,列车不仅在运行速度上逐步提高,运行密度上也在不断加大,因此如何保障列车运行的安全可靠性已成为目前亟需解决的重要问题.尤其针对高速运行的动车组,铁路部门提出了动车组运行故障动态图像检测系统(TEDS)[1],该系统利用轨边安装的线阵摄像机,采集运行中动车组的各个部位图像来进行故障自动识别,从而监测当前动车是否存在结构件的变化,并据此进行实时报警.
然而现有的动车组故障识别方法大多通过与历史图像相比较来找寻差异区域,从而定位故障位置.由于采集时间和维修业务等原因,容易造成历史图像所构成的模板库存在较大的类内差异性,需要不断地更新模板库,且现有方法难以保障故障检测的误报率与漏报率[2-5].模板库内的历史图像由于拍摄时间的不同,存在光照、成像像素不同,极易造成同一列车的成像尺度和成像像素存在较大的区别,因此误报率居高不下.此外,列车在修理时会出现部分零部件的更新换代或位置调整,均会使得模板库的类内差异性增大,从而增加误报率[6].为此,本文提出了一种无需预设模板的动车组故障识别算法,该算法将当前列车的其他车厢作为历史图像来进行图像比对,从而定位故障区域,有效提高了检测准确性.
本算法首先对列车组的车头车尾位置进行标定;然后根据车厢连接处存在对称图像的特征,进行车厢划分;最终将列车中的其他车厢作为历史图像,对该车厢进行故障自动监测.该算法不仅在较大程度上避免了光照、行车速度等外在干扰因素的影响,同时也不受零部件位置调整等人工修理模式的影响,从而有效地解决了当前故障识别中由于光照、列车运行速度等外在因素造成的误报率、漏报率较高等问题.
1 动车组故障识别算法
本文提出了一种无需预设模板的全新动车组故障识别算法,该算法无需任何历史模板图像,不必区分何种车型,只需根据当前采集的列车组图像自动进行图像检测,即可精准定位故障区域.算法总体流程框架如图1所示.

图1 动车组图像故障识别算法流程框架图Fig.1 Framework and flow chart of EMU image fault recognition algorithm
首先采用背景高斯差分法在采集的列车图像集中确定列车的车头和车尾图像;随后根据对称匹配技术定位到列车的车厢连接处位置;最终将动车组以车厢为单位构建成相应的列车图像.将列车中的其他车厢作为历史图像,对该车厢进行故障自动监测.
1.1 基于高斯混合模型的车头车尾定位技术
由于TEDS采用磁钢作为拍摄的触发信号,因此会采集到一部分固定的背景图像,随后才会有列车出现.鉴于此,本算法将线阵相机采集的图像作为视频帧进行处理,列车未到达时的图像设定为背景图像,采用高斯混合模型(GMM)[7-8]进行前景提取,确定列车的车头车尾区域.
鉴于动车图像数据是多维数据,为此本算法构建的GMM概率密度函数为
(1)
式中:z为采集的图像特征;μ为数据均值(期望);con为协方差计算符号;D为数据维度;p(z|θ)为该像素点属于背景的概率,若其大于阈值,则为前景图像.
具体的车头车尾位置标定算法流程如图2所示.首先将获取到的无任何列车信息的图像数据作为背景图像,并基于高斯混合模型进行建模,将其作为背景图像;随后分别从第一张或最后一张采集的列车图像开始进行背景差分,从而寻找是否出现前景图像.若出现,则继续定位前景图像位置,并输出车头和车尾的具体位置.在车头出现的图像中确定车头的具体位置来提取车头图像区域.在车尾出现的图像中确定车尾的具体位置,并提取车尾图像区域.

图2 基于高斯混合模型的车头车尾定位技术流程图Fig.2 Flow chart of front and rear positioning technology based on Gaussian mixture model
1.2 基于对称匹配技术定位车厢连接处
根据列车特点,其车厢连接处呈对称特征,为此本算法依据分析图像的对称指数来确定车厢连接处的区域.以动车组为例,其由至少两节带驱动力的车厢和若干节不带牵引力的车厢共同组成.其中,两节带驱动力的车厢为两节反向对称的动力车厢,即动车组的车头和车尾;而若干节不带牵引力的车厢,则为车头与车尾中间的车厢,且在任意两节车厢中间,即车厢连接处是彼此对称的.根据采集的列车组图像,动车组的车厢、车厢连接处和背景图像的颜色是不相同的,可以在列车组图像上首先将动车组车厢识别出来.对于其他区域,为了分辨出是车厢连接处还是背景图像,可以判断该区域的两侧图像是否对称:若对称,则表示该区域为车厢连接处;反之,则为背景图像.
本算法根据Peter Kovesi的研究[9],基于相位信息进行对称性检测.首先定义n个尺度、η个方向的小波滤波器对,并将像素p映射为能量,即
(2)
式中:k=1,2,…,n;q=1,2,…,η;E为能量熵.通过上述方法对原始图像进行滤波并映射为能量,其中相位均为0的能量最大点,即为图像中物体的对称点.根据该图像的PSDE值,确定该图像中是否存在对称图像,进而判定是否有车厢连接处.
1.3 基于车厢图像的故障识别算法
自动识别出列车组的车头和车尾位置,并去除背景图像后,按照车厢连接处位置将列车采集的图像进行拼接分割,从而构成每一节完整的车厢图像,再通过与列车中其他车厢进行SIFT特征[10-11]匹配,实现故障定位算法.
针对当前采集的完整车厢图像,采用尺度不变特征变换(SIFT)和非极大值抑制(NMS)[12-15]来定位故障区域,完成运行动车组的可视结构异常情况实时分析与自动预警.首先,使用高斯差分尺度空间(DOG)提取图像中的尺度空间极值变化,即
D(x,y,σ)=(G(x,y,kσ)-G(x,y,σ))*I(x,y)=
L(x,y,kσ)-L(x,y,σ)
(3)
式中:(x,y)为图像的像素位置;σ为尺度空间因子;*为卷积运算符号;L(x,y,σ)定义为原始图像I(x,y)与一个可变尺度的2维高斯函数G(x,y,σ)的卷积运算.
随后提取感兴趣点的方向和特征描述,在每个感兴趣点的周围,基于图像局部的梯度方向分配给每个关键点位置一个或多个方向.接着以兴趣点为中心取16×16像素的窗口,并将其划分为4×4个子区域.其次在每4×4个像素的图像块上计算8个方向的梯度方向直方图,并绘制每个梯度方向的累加值,即可形成一个种子点.由于图像区域共存在16个种子点,因此对于每个兴趣点可以产生4×4×8共128维的SIFT特征向量,即SIFT描述子.每个兴趣点的方向参数依靠兴趣点邻域像素的梯度方向分布特性来确定,梯度方向分布特性使算子具备了旋转不变性.
随后通过非极大值抑制算法,根据故障点的区域位置确定车厢图像中的初步故障区域,故障识别的算法流程如图3所示.首先,提取当前采集列车运行图像的尺度不变特征变换描述子特征;随后采用非极大抑制值,根据图像中预设故障点、感兴趣点的区域位置及区域分数来定位图像中的初步故障区域;最终将该趟列车非本节车厢的其他图像数据作为图像模板库,为这些故障区域在图像模板库中寻找相应的位置.若匹配成功,则表明该图像为正常区域;若匹配阈值较低,则说明该图像中含有故障区域,需对故障区域进行定位.

图3 基于车厢图像的故障识别算法流程Fig.3 Flow chart of fault recognition algorithm based on compartment images
2 实验与分析
实验首先构建TEDS图像集,并利用该数据集对本算法进行性能评价,随后与现有的图像故障识别算法进行对比分析.实验车型分为:CRH1A、CRH2A、CRH3A、CRH5A、CRH380A、CRH380B及复兴号7种车型,列车通过TEDS设备实时采集运行图像.其中CRH1A型采集大约3 000张图像;CRH2A型采集大约3 100张图像;CRH3A型采集大约2 500张图像;CRH5A型采集大约3 100张图像;CRH380A型采集大约3 200张图像;CRH380B型采集大约3 200张图像;CRH400型(复兴号)采集大约4 500张图像.采集的图像分别包括:列车的底部高清图像(制动装置、驱动装置、牵引装置、转向架、轮轴、车钩及车底部其他部位)和侧面的裙摆、转向架等部位图像.图4分别显示了沉箱与侧箱摄像头采集的车辆图像.

图4 TEDS采集的部分底部和侧部图像Fig.4 Part of bottom and side images acquired by TEDS
首先测试算法的故障识别性能,本实验与传统的SIFT特征匹配算法分别在漏报率、误报率和识别时间3个标准上进行评估.漏报率是指在故障检测中存在N次故障有M次未能检测出;而误报率是指在检测出的N次故障中,其中有M次不是故障;识别时间是指从算法开始运行到算法运行结束所花费的时间.本算法运行在研华IPC-810E机型上,其CPU为Intel Core 2 E7400双核双线程,采用Windows XP SP3系统.表1显示了本算法与传统算法对于不同车型的故障识别性能方面的比较.由表1可见,CRH380的误报率较低,主要原因是该车型行驶的频率较高,基本上各种替换零件在TEDS系统上都采集过,因此该车型获取的图像类内差异性较小,对算法的性能影响较少;而CRH1 A型列车误报率相对较高,主要原因是该车型采集的图像质量较差,且其更换零部件的频率较低,很难完全获取到所有类型的替换零部件,从而造成较高的误报率;CRH400为最新的复兴号,因为该车型整体运行时间较少,磨损程度轻,此外,零配件统一,使得算法的故障识别难度降低,因此算法的性能最好,在漏报率12%的情况下,可以达到零误报.综上所述,本文算法针对所有车型的漏报率均相对较低,主要原因是本算法不仅在较大程度上避免了光照、行车速度等外在干扰因素的影响,也可以不受零部件位置调整等人工修理模式的影响,从而可以较好地对运行过程中的动车组进行隐蔽故障的实时预警.

表1 本文故障识别算法与传统SIFT算法的性能比较Tab.1 Performance comparison between as-proposed fault recognition algorithm and traditional SIFT algorithm
通过图像的形式讨论本算法对于车头、车底及车厢连接处的划分情况,如图5所示,本算法对实验车型均可取得准确的车头和车底位置,并裁剪出相应的图像.但对车厢连接处的划分性能有所下降,其主要原因是TEDS在列车抵达压塌磁钢时才启动线阵相机,开始拍照.根据背景差分,前景提取完全可以准确地获取各种车型的车头和车尾图像.但车厢连接处拍摄时处于照片中的区域限制,会造成不对称.为此,本算法在实际应用中,通常将几幅图像串联后再进行分析,从而避免错过车厢连接处区域.

图5 TEDS采集的部分车头、车底、车厢连接处图像Fig.5 Part of front,bottom and joint images collected by TEDS
表2展示了本算法针对不同时间、不同摄像头采集火车图像的故障识别性能.可以看出,本算法针对侧箱摄像头的故障识别率相对较高,主要因为火车侧面的零部件相对较少,图像的局部角点信息不明显,仅在故障出现时会大量增加角点信息,因此利用本算法可较好地圈定故障的大致位置.另外,列车底部含有大量的零部件,使得图像具有较为丰富的角点信息,而故障导致的新增角点信息难以利用SIFT特征匹配准确获取.特别是一些细小的故障,如螺栓丢失、管道裂纹等问题,在一定程度上加大了特征匹配的难度,从而限制了算法的故障识别效果.为此,将会在后续的工作中引入空间邻域位置信息,从特征和空间信息相融合的角度提升算法的性能.特别需要指出的是,随着列车维修后运行时间的变化,采集的图像类内差异性会很大,因此本文对列车维修运行一天后和一个月后的故障识别率进行了统计比对.
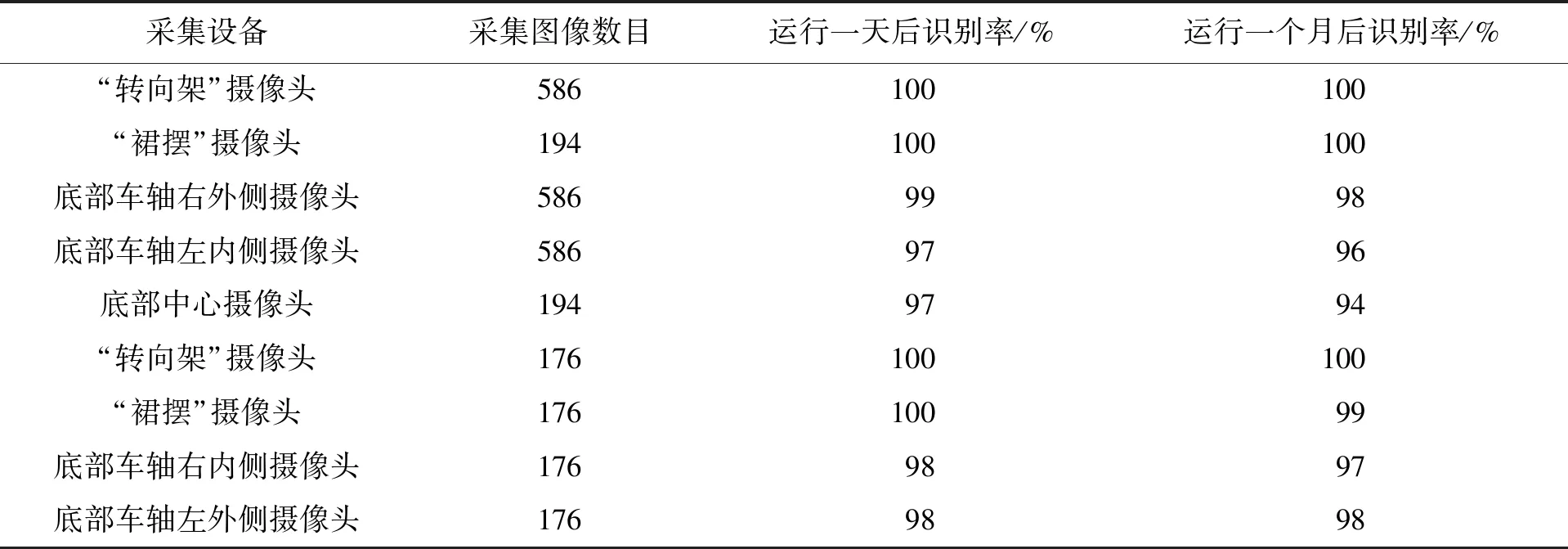
表2 不同时间与摄像头采集图像的故障识别率Tab.2 Fault recognition rate of images collected by different cameras at different time
第2组实验主要分析阈值参数对算法的影响.本算法共涉及两个阈值参数,分别是SIFT特征匹配阈值和模板匹配阈值,具体的性能比较如表3所示.可以看出,当SIFT特征匹配选取较小阈值时,故障识别性能较差.说明当阈值较低时,未匹配上的SIFT特征点数相对较多,因此相应的误报率较高.而随着SIFT特征匹配阈值的逐步增加,故障识别准确率也在稳步提升.但当阈值大于一定值后,阈值继续增加,故障识别性能反而有所降低.主要原因是阈值过高,虽在一定程度上减少了误报率,但漏检的特征点数却随之相对增加,导致漏报率有所提升.对于模板匹配的阈值,从表3中可看出其变化趋势与SIFT特征匹配的基本相似.为此综合分析上述两个阈值,本算法选取故障识别性能较优时采用的阈值参数,即模板匹配算法选取阈值为0.7,SIFT特征匹配阈值为0.9.

表3 阈值参数对故障识别率的影响Tab.3 Influence of threshold parameters on fault recognition rate
3 结 论
针对动车组运行故障检测问题,本文提出了一种无需预设模板的动车组故障识别算法.首先识别列车组的车头车尾,然后根据图像之间的相关性、图像自身的特性识别列车组的车厢连接处;再与待检测列车组的其他车厢图像进行模板匹配,并在无需根据列车车型寻找历史车辆模板库的前提下实现故障识别,从而完成运行动车组可视结构异常情况的实时分析与自动预警.实验结果表明,本算法针对运行动车组的异常情况能够有效地分析预警,使得系统用户可及时发现重大故障,从而提升动车运营质量.
