基于混沌同步与迁移控制的隔振系统线谱控制方法
2021-09-27左兆伦刘树勇
左兆伦,俞 翔,李 爽,柴 凯,刘树勇
(1.海军工程大学 动力工程学院,武汉 430033;2.海军工程大学 舰船与海洋学院,武汉 430033)
混沌控制是混沌领域的一个重要分支,它在混沌应用中起到至关重要的作用。Hubler[1]最早对混沌控制展开研究,随后Ott等[2]提出OGY法,之后国内外学者陆续提出了多种混沌控制方法,并将其广泛应用于保密通信[3]、生物系统[4]、混合流体[5]、耦合映射[6]等诸多领域。在机械工程领域,朱石坚等[7]提出混沌隔振方法,利用强非线性隔振系统(vibration isolation system,VIS)处于混沌状态时响应功率谱呈连续谱的特征,降低动力机械周期性运转产生的低频线谱。Lou等[8]通过数值分析和试验研究对该理论进行了原理验证。当前使非线性隔振系统混沌化的方法主要有3类:一是设计强非线性隔振系统,并调整其参数使之处于混沌振动状态,由于混沌系统对参数极为敏感,该方法在变工况环境下难以实现持续混沌运动;二是反馈自适应控制方法[9-12],这类方法能够有效降低低频线谱,但是必须有一个力直接作用于被隔振设备或者基座上,需要较大的外加能量并且容易放大设备振幅,此外,投影同步方法需要与原系统等量的控制输入能量,在实际应用中存在时滞问题;三是广义混沌同步方法,具体又可以分为参数驱动[13-15]和状态驱动[16]两种方法。状态驱动方法仍然存在控制能量较大的问题,参数驱动方法对系统变量参数进行驱动,利于降低能耗。然而,由于非线性因素的影响,混沌同步系统中可能存在多个稳定的混沌吸引子,不同吸引子的频谱特征和线谱强度可能相差较大,线谱控制效果与系统所处的吸引子密切相关。
在多吸引子系统中,通过施加吸引子迁移控制可以实现不同运动状态之间的转换。最早的迁移控制方法是Jackson等[17-18]提出的开环控制和参数开环控制,Jackson等[19-20]将开环控制和线性反馈相结合,提出了开环加闭环(open-plus-closed-loop,OPCL)控制,并给出了两种迁移方案即将系统状态从一个吸引子迁移至构造的目标轨道或者另一个“目标”吸引子,以及一种确定近似动力学模型的试验搜索方法。随后,OPCL控制算法吸引了国内外学者的广泛关注,王杰等[21]针对连续多项式混沌系统,分析OPCL控制的输运域并进行算法优化,提出了开环加非线性闭环(open-plus-nonlinear-closed-loop,OPNCL)控制。柴凯等[22]针对两自由度非线性隔振系统,通过全局分岔分析找出共存吸引子,利用OPCL控制和OPNCL控制等算法实现了周期吸引子之间、周期和混沌吸引子之间的迁移控制。俞翔等[23]针对柔性基础准零刚度隔振系统,利用OPCL控制实现了周期吸引子之间的迁移控制,并分析其稳定性和可行性。此外,OPCL控制算法还被推广至同步控制领域的理论研究和工程应用[24-25]。
本文以柔性基础非线性隔振系统为研究对象,对其施加广义同步控制,分析混沌同步系统的多吸引子共存现象以及不同吸引子对应的线谱控制效果,对不同迁移控制方法展开算法研究和稳定性研究,尝试将同步系统从大振幅混沌吸引子迁移至小振幅混沌吸引子,重构频谱特征并降低特征线谱强度,实现稳定性强、能耗低、振幅小的隔振系统线谱混沌化控制。
1 混沌同步系统
1.1 广义同步控制
在只考虑一阶模态时,柔性基础非线性隔振系统可以简化为双层质量-弹簧系统,如图1所示。M1和M2分别为被隔振设备和基座的质量。M1由具有线性刚度K1和三次非线性刚度K3的非线性隔振器、阻尼系数为C1的阻尼器共同支撑。M2由等效线性弹簧K2和线性阻尼C2共同支撑。在设备和基座之间安装作动器以施加广义同步控制和迁移控制。选取弹簧自然长度状态下,质量块所处位置为坐标原点,简谐激励下柔性基础非线性隔振系统的动力学方程为
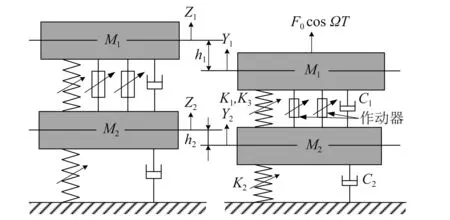
图1 柔性基础非线性隔振系统Fig.1 Model of the nonlinear VIS with flexible base
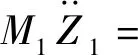
K3(Z1-Z2)3+F0cosΩT-M1g,
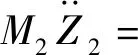
K1(Z1-Z2)+K3(Z1-Z2)3-M2g
(1)
当选取系统处于静平衡状态时,质量块所处位置为新坐标原点,假设M1和M2在新旧坐标系下的位移之差分别为h1和h2,则有下列关系:Z1=Y1-h1,Z2=Y2-h2。以及如下受力关系:M1g=K1H+K3H3,M1g+M2g=K2h2。其中:H=h1-h2。代入式(1)得
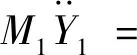
3K3H(Y1-Y2)2-K3(Y1-Y2)3+F0cosΩT,
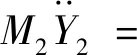
(K1+3K3H2)(Y1-Y2)-
3K3H(Y1-Y2)2+K3(Y1-Y2)3
(2)
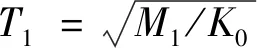
(3)
将式(3)代入式(2),可得一阶形式的无量纲动力学方程
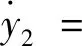
(y1-y3)3+fcos(ωt),
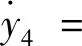
ελ(y1-y3)2+ε(y1-y3)3
(4)
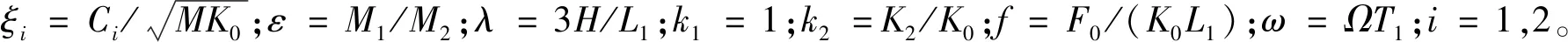
采用参数驱动的单向耦合广义同步方法,混沌驱动系统选为简谐激励下的单自由度振子
(5)
其参数设置为ω1=3.931 1,w=4,v=3,u=0.15,d=9,初始条件(x1,x2)设置为(0,0)。以柔性基础非线性隔振系统为响应系统,利用驱动系统的输出信号x2对其线性刚度k1进行驱动,即k1=kx2,其中k为耦合强度。响应系统的动力学方程可改写为
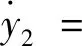
(y1-y3)3+fcos(ωt),
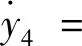
ελ(y1-y3)2+ε(y1-y3)3
(6)
1.2 吸引子共存
设备振动通过基座向船舶壳体传递,下面分析基座的响应特性。在式(4)中,设置系统参数为:ε=0.2,λ=1,k2=2,f=20,ξi=0.8,i=1,2。以激励频率ω为变化参数,分别进行向前延拓(ω取值为2~10)和向后延拓(ω取值为10~2)的全局分岔分析。如图2所示,在不同初始条件下,系统响应振幅发生跳跃的参数区间为ω∈[3.69,4.45]。在该参数区间内,响应系统存在两个共存吸引子,而线谱控制效果可能与系统所处的吸引子密切相关。
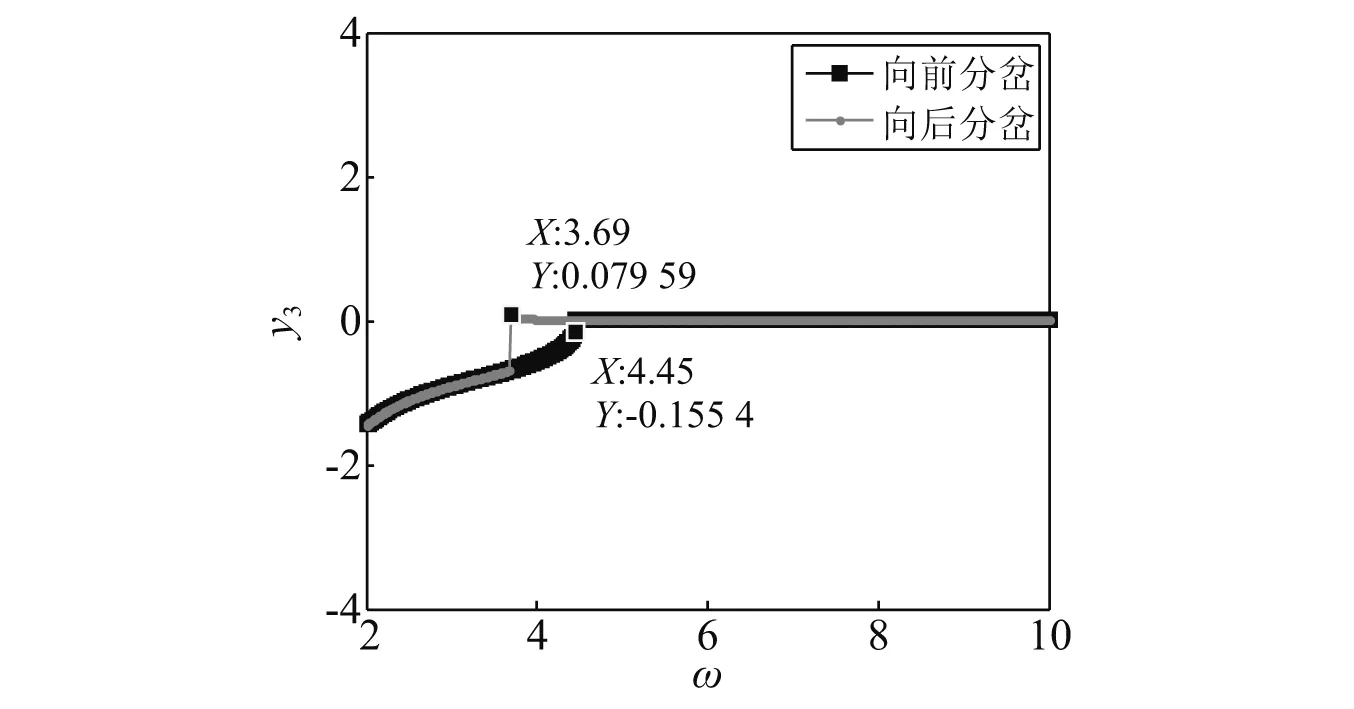
图2 响应系统随ω变化的全局分岔图Fig.2 Global bifurcation of the response system varying with ω
在式(6)中,保留式(4)的参数设置,令ω=3.931 1,k=0.1。设置初始条件(y1,y2)=(0,-5),以(y3,y4)分析平面,利用胞化积分轨迹法[26]得到两个共存吸引子对应的吸引域分布图,如图3所示。浅色区域和深色区域分别为大振幅吸引子A1和小振幅吸引子A2的吸引域。根据吸引域图选取不同的初始条件,设置两组对照组和扰动组,求得基座响应的时间历程图。如图4(a)所示,第一组初始条件的对照组和扰动组分别为(0,-5,0,0)和(0,-5,0.5,0.5),基座经历瞬态并最终稳定于大振幅混沌吸引子;如图4(b)所示,第二组初始条件的对照组和扰动组分别为(0,-5,2,0)和(0,-5,2.5,0.5),基座经历瞬态后将稳定于小振幅混沌吸引子。在具有初值敏感性的混沌同步系统中,两个吸引子都有其对应的吸引域,即从同一吸引域出发的相轨迹都将渐进稳定于该点所属的吸引子,从不同吸引域出发的相轨迹将运行于不同的吸引子,说明共存吸引子具有渐进稳定性。
与生理盐水组比较,各剂量组雌性大鼠的肝、肾、脑、胸腺、卵巢和子宫的脏/体比无显著性差异。各剂量组雌性大鼠的肾上腺和脾的脏/体比部分有显著性差异,但是综合考虑脏器的重量和大鼠的终期空腹体重,认为其差异无实际生物学意义。
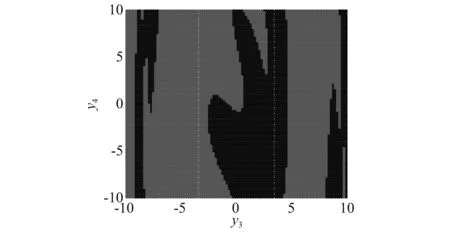
图3 基座中共存吸引子的吸引域Fig.3 The attraction basins of coexisting attractors in the base
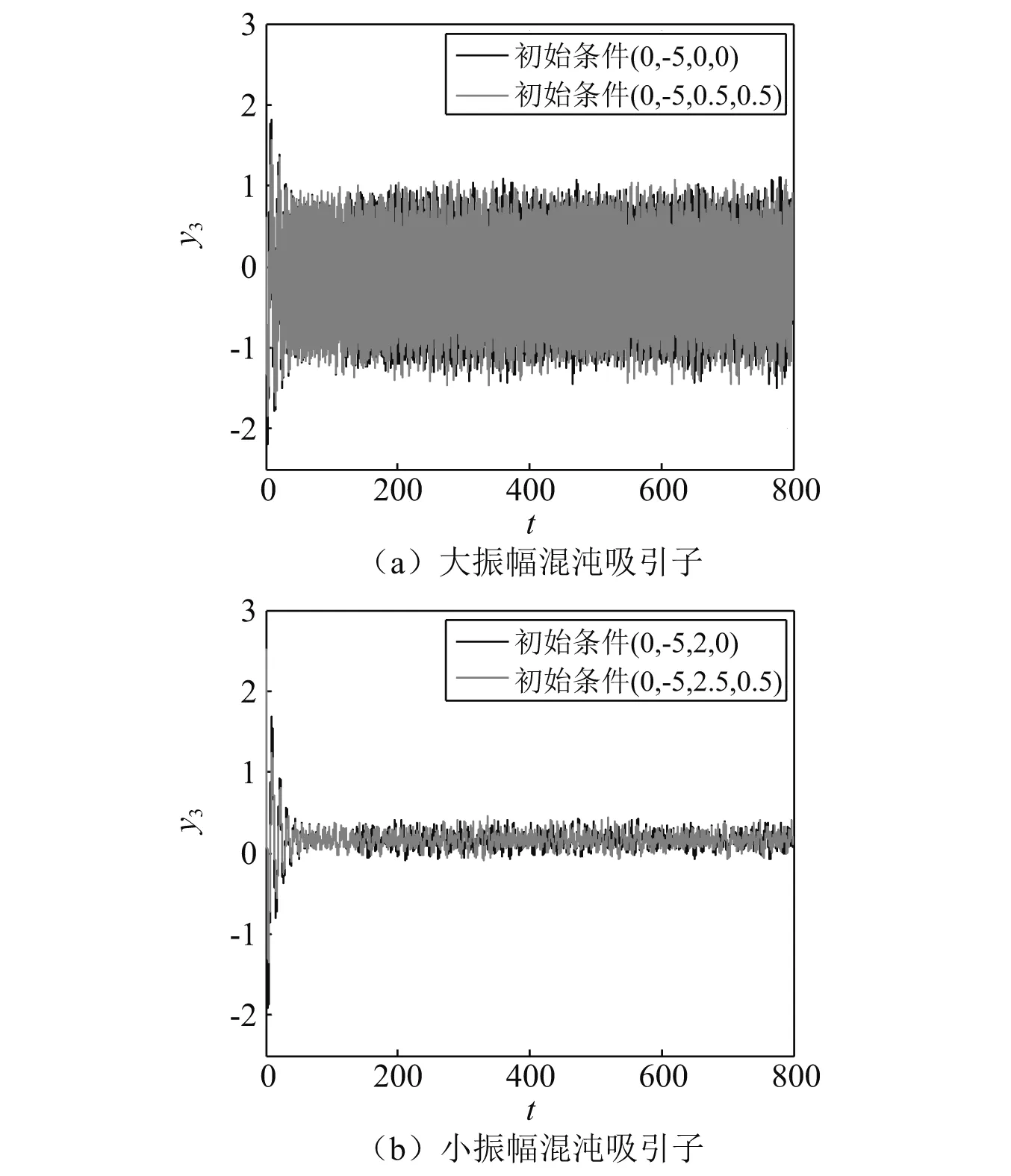
图4 不同初始条件下共存吸引子的时间历程图Fig.4 Time histories of the coexisting attractors under different initial conditons
1.3 线谱控制效果
未受驱动时,基座的相图和位移功率谱如图5(a)和图6(a)所示。由图可知:两吸引子的相轨迹均为极限环,庞加莱映射均为一个不动点,位移功率谱图呈现明显线谱特征,说明共存的两个吸引子均为周期吸引子。受驱动时,共存吸引子的相轨迹和功率谱如图5(b)和图6(b)所示。相轨迹缠绕在一起并遍布在一定的相空间范围内,功率谱呈现连续谱特征,说明共存的两个吸引子被转换为混沌吸引子,混沌同步方法能够实现隔振系统的持续混沌化。
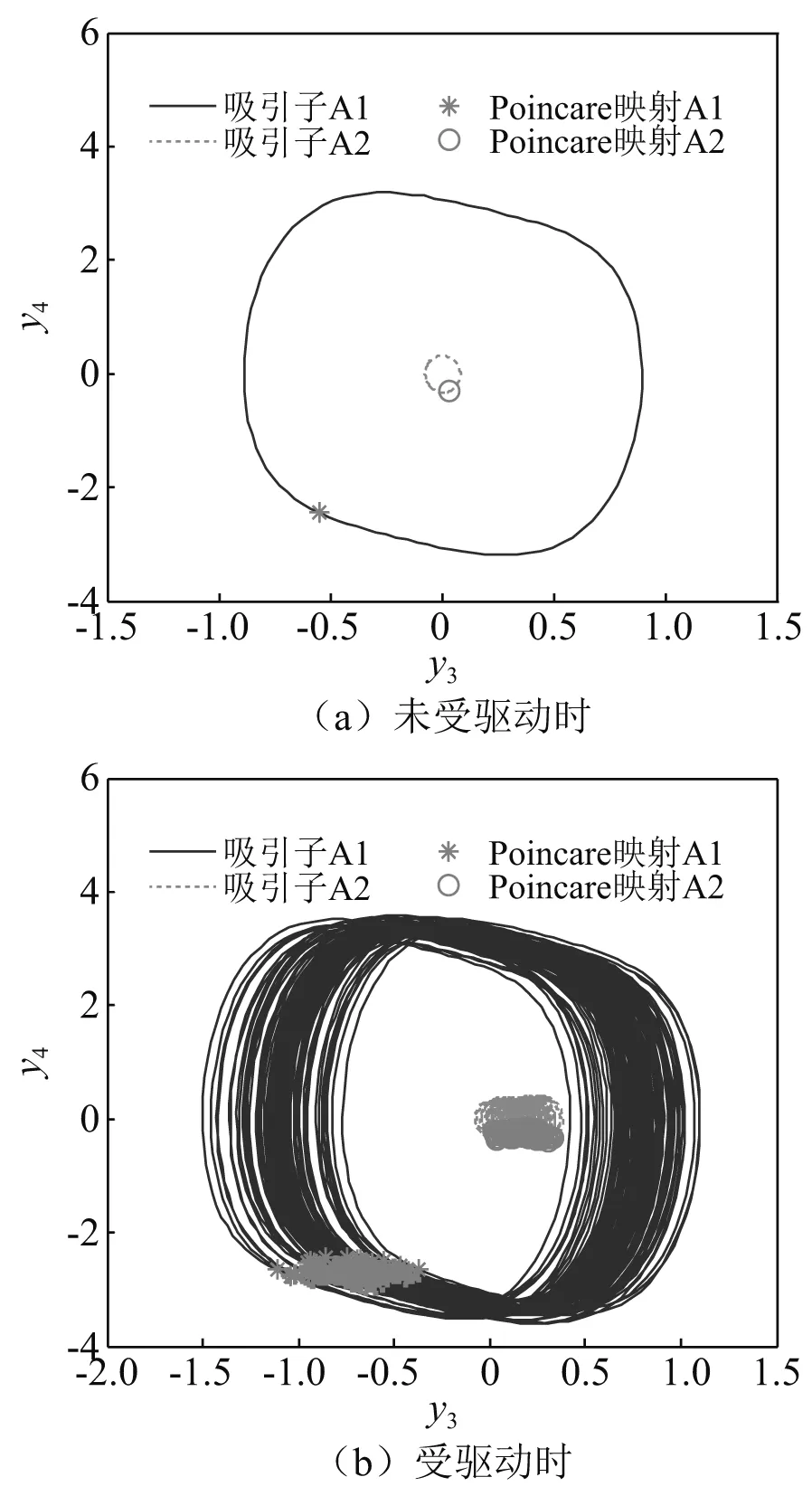
图5 基座中共存吸引子的相图Fig.5 Phase diagram of coexisting attractors in the base
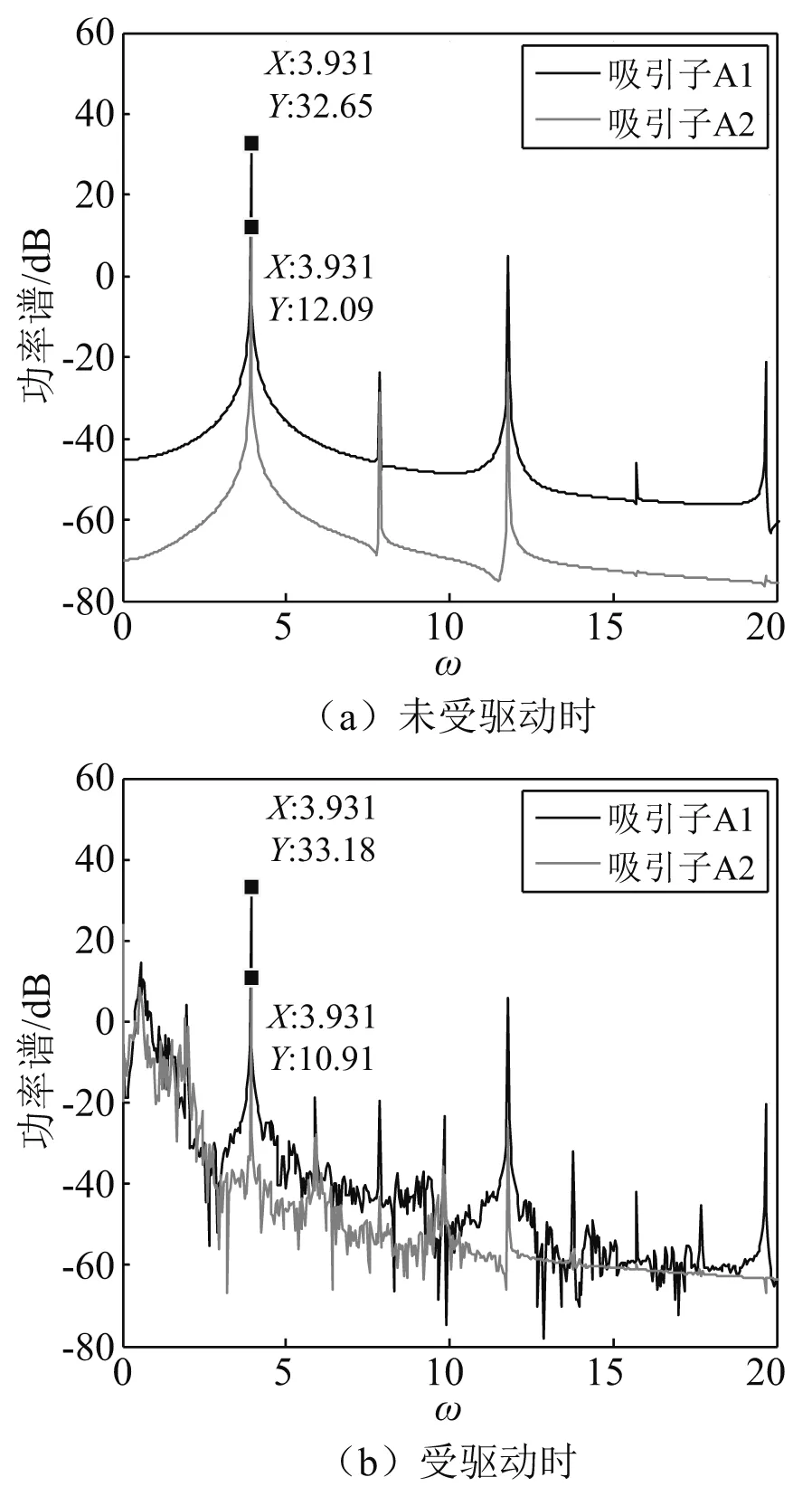
图6 基座中共存吸引子的位移功率谱Fig.6 Power spectrum of coexisting attractors in the base
在隔振系统受驱动时,两个吸引子的特征线谱强度较未受驱动时没有明显增加。在混沌同步系统中,混沌吸引子A1和A2在ω=3.931 1处的特征线谱强度分别为33.18 dB和10.91 dB,后者比前者小22.7 dB,说明混沌同步化方法的线谱控制效果取决于同步系统所处的吸引子,当系统运行于小振幅混沌吸引子时,线谱控制效果将大幅提高。
分别设置响应系统初始条件为(0,-5,0,0)和(0,-5,2,0),未受驱动和受驱动时被隔振设备M1中两个吸引子的时间历程图如图7(a)和图7(b)所示。由图可知:在隔振系统受驱动时,两个吸引子的振幅较未受驱动时几乎没有变化,说明隔振系统的隔振性能不受同步控制影响。
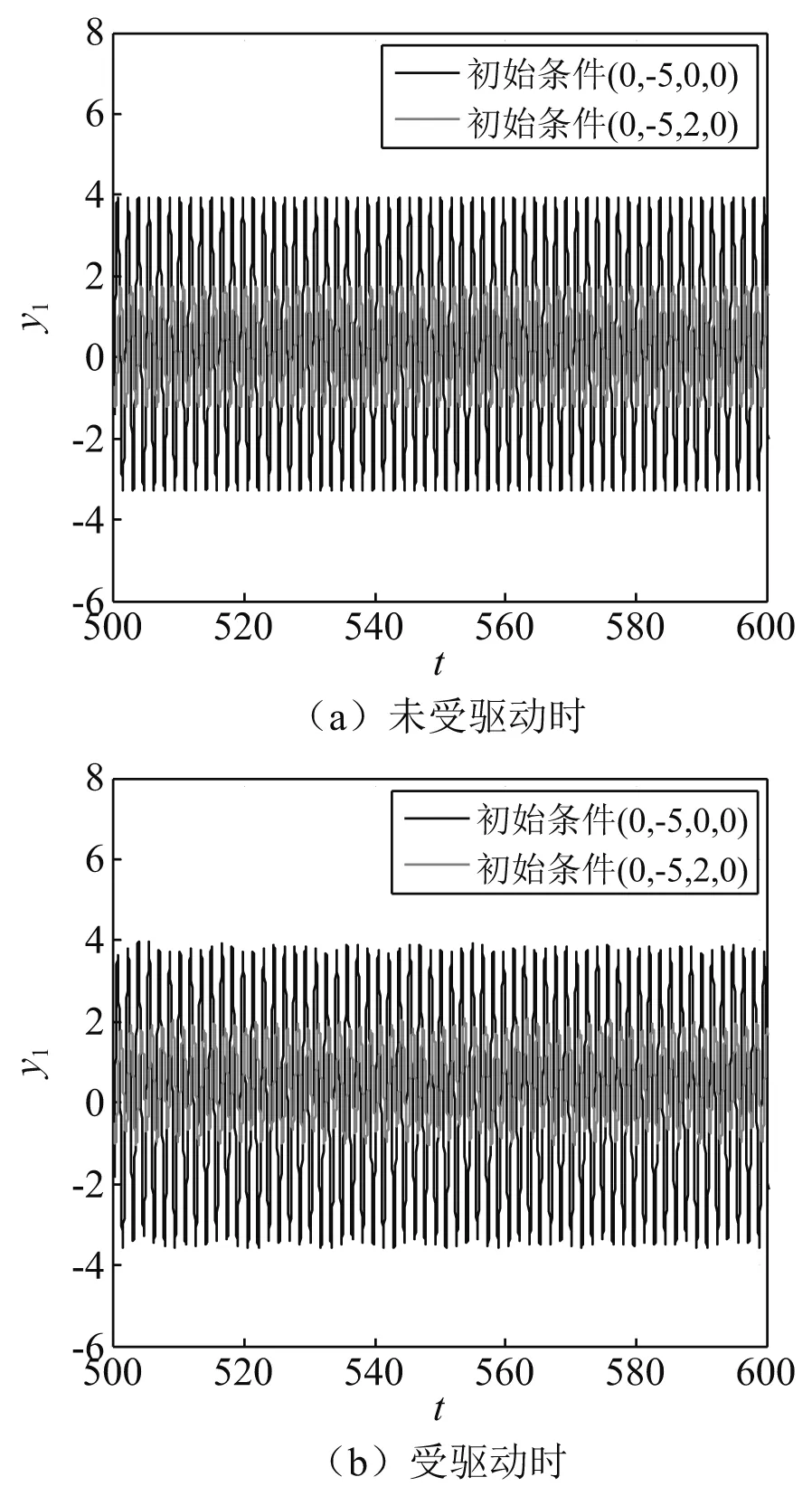
图7 被隔振设备M1的时间历程图Fig.7 Time histories of the equipment M1
2 迁移控制算法
考虑包含迁移控制项的动力学方程
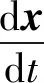
(7)
式中:F(x,t)为混沌同步系统的动力学方程;S(t)为开关函数,当关闭控制开关时,令S(t)=0,当启动控制开关时,令0 为便于分析,将式(5)和式(6)中左边各项记为 F(x,y,t)=(F1,F2,F3,F4,F5,F6)= (8) F1(g,t)=g2, F3(g,t)=g4, F4(g,t)=-ξ1(g4-g6)-kg2(g3-g5)+λ(g3-g5)2- (g3-g5)3+fcos(ωt), F5(g,t)=g6, F6(g,t)=-εξ2g6-εk2g5+εξ1(g4-g6)+ε(g3-g5)- εξ(g3-g5)2+ε(g3-g5)3 (9) 引入开环控制算法 (10) 式中,dg/dt≠F(g,t)。 引入线性反馈控制算法 K(g,x,t)=A[x(t)-g(t)] (11) 式中,A=(aij)6×6为任意负定的实常数对角阵。 引入OPCL控制算法 式中:D(g,t)=A-∂F(g,t)/∂g;∂F(g,t)/∂g为F(g,t)关于目标函数g(t)的雅可比矩阵。 引入OPNCL控制算法 N(g,t)[x(t)-g(t)] (13) 选取负定对角阵A=diag(-10,-10,-10,-10,-10,-10)及目标轨道 (14) 对同步系统施加开环控制,并代入式(7),得到 (15) 对同步系统施加线性反馈控制,代入式(7),得到 (16) 对同步系统施加OPCL控制,代入式(7),得到 (17) 对同步系统施加OPNCL控制,代入式(7),得到 (18) 吸引子迁移控制的基本原则是对原系统施加控制,使得受控系统的目标轨道存在局部稳定区域与共存吸引子的吸引域部分重叠,当原系统运行到重叠部分时,启动控制,这样受控系统就可沿着该稳定轨道运行。当该轨道的起点在一个吸引子上,终点在另一个吸引子的吸引域时,则可以实现从一个吸引子到另一个吸引子的迁移控制。 分别对不同控制算法作用下的吸引子迁移过程进行数值仿真,浅灰虚线为系统的初始状态,黑色点划线为打开控制开关时系统的状态,深灰实线为关闭控制开关时系统的状态。在开环作用下,基座的相轨迹和时间历程图如图8(a)和图8(b)所示,系统无法被迁移至目标轨道,说明开环控制不适用于混沌吸引子之间的迁移控制。 图8 开环控制下,基座的相轨迹和时间历程图Fig.8 The phase trajectories and time histories of the base under the open-loop control 在线性反馈控制、OPCL控制、OPNCL控制下,基座的相轨迹和时间历程图,分别如图9(a)、图10(a)、图11(a)和图9(b)、图10(b)、图11 (b)所示。3种控制方法均能实现同步系统中混沌吸引子之间的迁移转换。由图可知:初始时,系统运行于大振幅混沌吸引子;当系统运行至大振幅混沌吸引子与目标轨道g(t)邻域的重叠区域时,启动控制,系统迅速迁移至目标轨道g(t)或g(t)的邻域;当系统运行至目标轨道g(t)邻域与小振幅混沌吸引子对应吸引域的重叠区域时,关闭控制,系统逐渐迁移并最终稳定运行于小振幅混沌吸引子。经过上述迁移过程,实现了混沌同步系统从大振幅混沌吸引子到小振幅混沌吸引子的迁移转换。在线性反馈控制下,系统不能精确运行于目标轨道,而是运行于目标轨道附近邻域,从目标轨道迁移至小振幅吸引子的瞬态振幅比OPCL控制和OPNCL控制都小。在OPCL控制和OPNCL控制作用下,基座的相轨迹和时间历程图几乎完全一致。此外,在迁移过程结束后,迁移控制开关函数保持关闭状态,意味着不需要持续施加控制能量,满足实际工程应用中的低能耗需求。 图9 线性反馈控制下,基座的相轨迹和时间历程图Fig.9 The phase trajectories and time histories of the base under the closed-loop control 图10 OPCL控制下,基座的相轨迹和时间历程图Fig.10 The phase trajectories and time histories of the base under the OPCL control 图11 OPNCL控制下,基座的相轨迹和时间历程图Fig.11 The phase trajectories and time histories of the base under the OPNCL control 对开环控制,将式(10)代入式(7),F(e+g,t)在g(t)附近对F(e+g,t)进行泰勒级数展开,可得误差方程 (i=1,2,3,4,5,6) (19) 对线性反馈控制,将式(11)代入式(7),则得 (20) (i=1,2,3,4,5,6) (21) 对OPCL控制,将式(12)代入式(7),可得 (i=1,2,3,4,5,6) (22) 将式(9)和目标轨道函数式(14)代入式(22),得到 (23) 对OPNCL控制,将式(13)代入式(7),可得 (24) 开环控制不能实现有效迁移控制,线性反馈控制的误差方程比开环控制多包含表达式Ae,由于A是负定矩阵,该项利于迁移控制趋于稳定,并且A中各常数项绝对值越大,稳定效果越好。 线性反馈控制对目标轨道g(t)的选取有严格的限制要求,文中选取的目标轨道并非同步系统的固有嵌入轨道,因而系统不能精确运行于目标轨道,而是运行于目标轨道附近邻域,并且由于控制算法简单,线性反馈控制的系统瞬态振幅较小。 OPCL控制由开环部分和闭环部分组成,开环部分构造出需要的目标轨道,闭环部分使控制系统趋于稳定。在OPCL控制的基础上,OPNCL控制算法增加一项非线性项N(g,t),使得受控系统的误差方程不包含目标轨道函数g(t),具有全局稳定的输运域,鲁棒性更强,并且完成迁移过程所需时间更短。在OPCL控制和OPNCL控制作用下,基座吸引子迁移轨迹几乎完全一致。这是因为选取的合适目标轨道函数g(t)使得OPCL控制和OPNCL控制的算法接近等价,这一点通过误差方程式(23)和式(24)也能看出。此外不难发现,只需选择合适的混沌驱动系统和目标轨道g(t)使得N(g,t)=0,便可令OPCL控制和OPNCL控制完全等价。在工程应用中,不同的迁移控制算法各有适用范围,应当结合算法鲁棒性、能耗限制、迁移时间、瞬态振幅等实际工况需求选择合适的迁移控制算法。 本文提出了一种基于混沌同步与迁移控制的船舶机械设备隔振系统线谱控制方法,通过理论研究和数值仿真证明了其可行性,得出结论如下: (1)混沌同步方法能够实现隔振系统的持续混沌化并保持隔振性能,混沌同步系统中有多个稳定的混沌吸引子共存,线谱控制效果取决于同步系统所处的吸引子。 (2)选择合适的迁移控制方法能够使同步控制下的隔振系统稳定运行于小振幅的混沌运动,从而降低特征线谱强度,并且该方法具有稳定性强、能耗低的特点。 (3)线性反馈控制、OPCL控制和OPNCL控制均能实现同步系统中混沌吸引子之间的迁移控制。在线性反馈控制作用下,同步系统不能精确运行于构造的目标轨道,而是运行于目标轨道附近邻域;选择合适的混沌驱动系统和目标轨道g(t),可使OPCL控制和OPNCL控制算法接近等价甚至完全等价。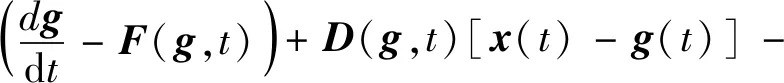
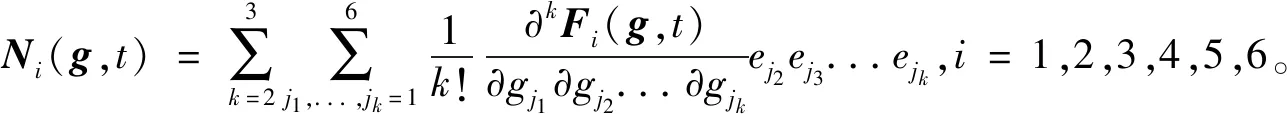
3 数值仿真
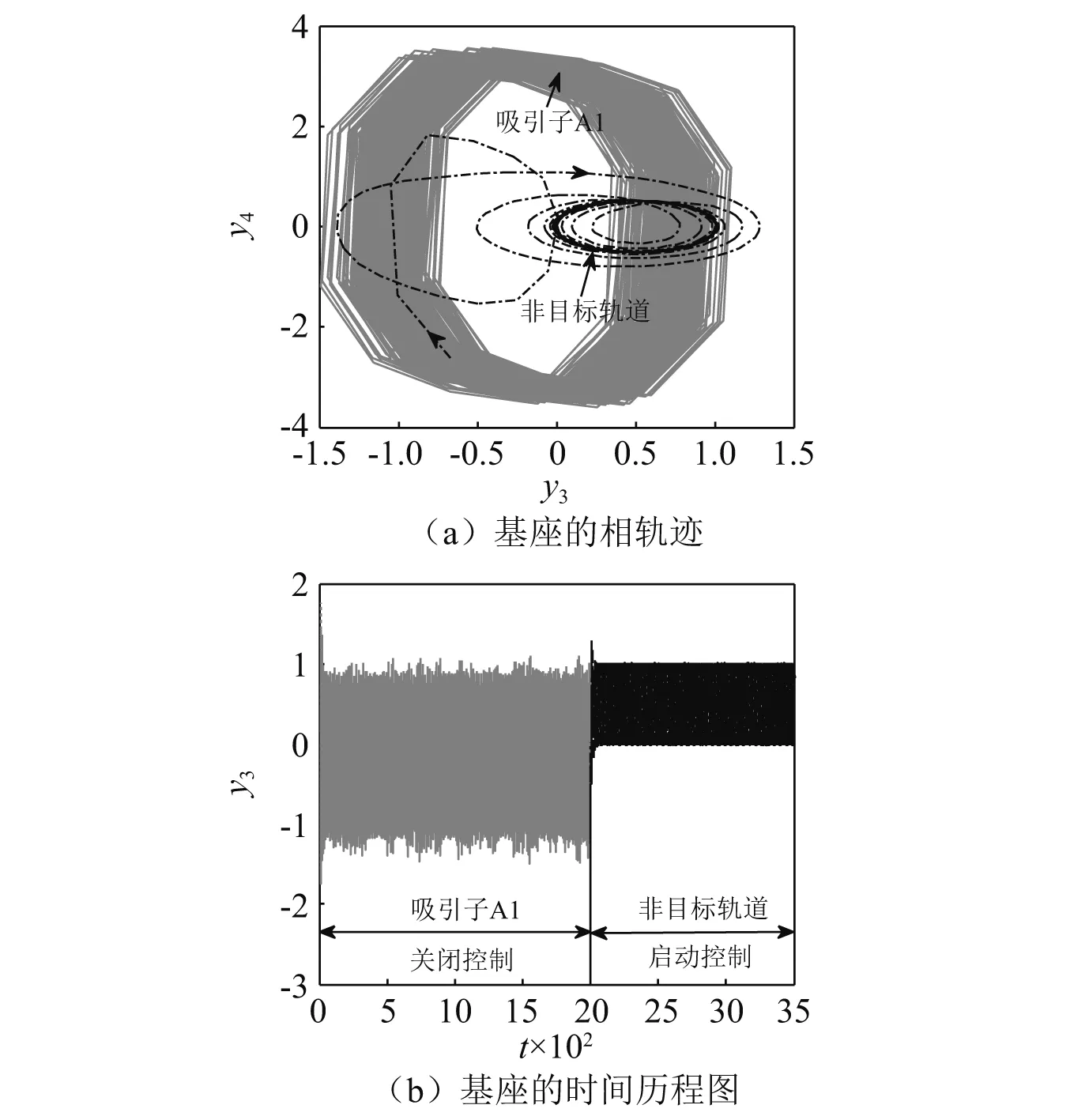
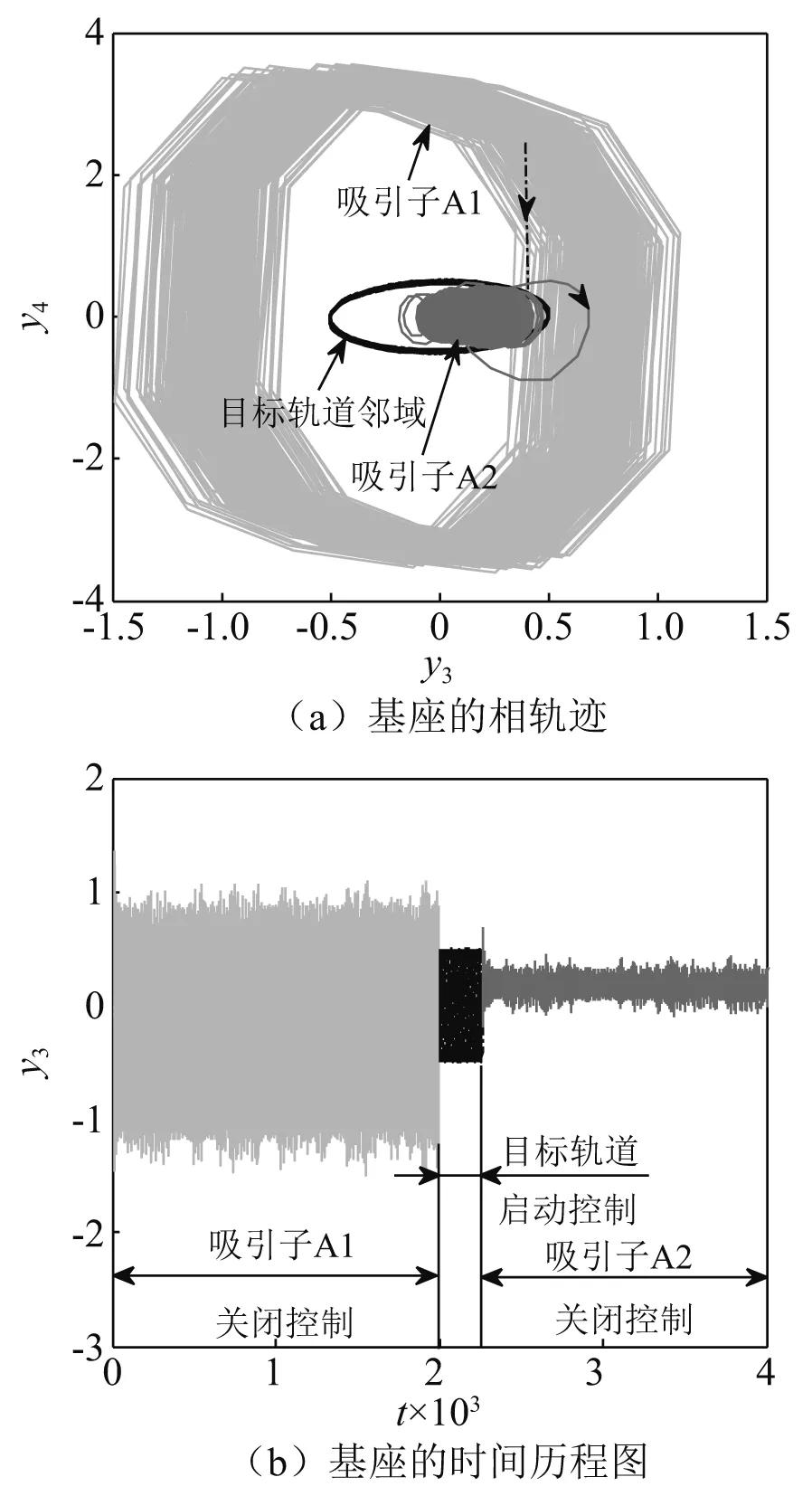
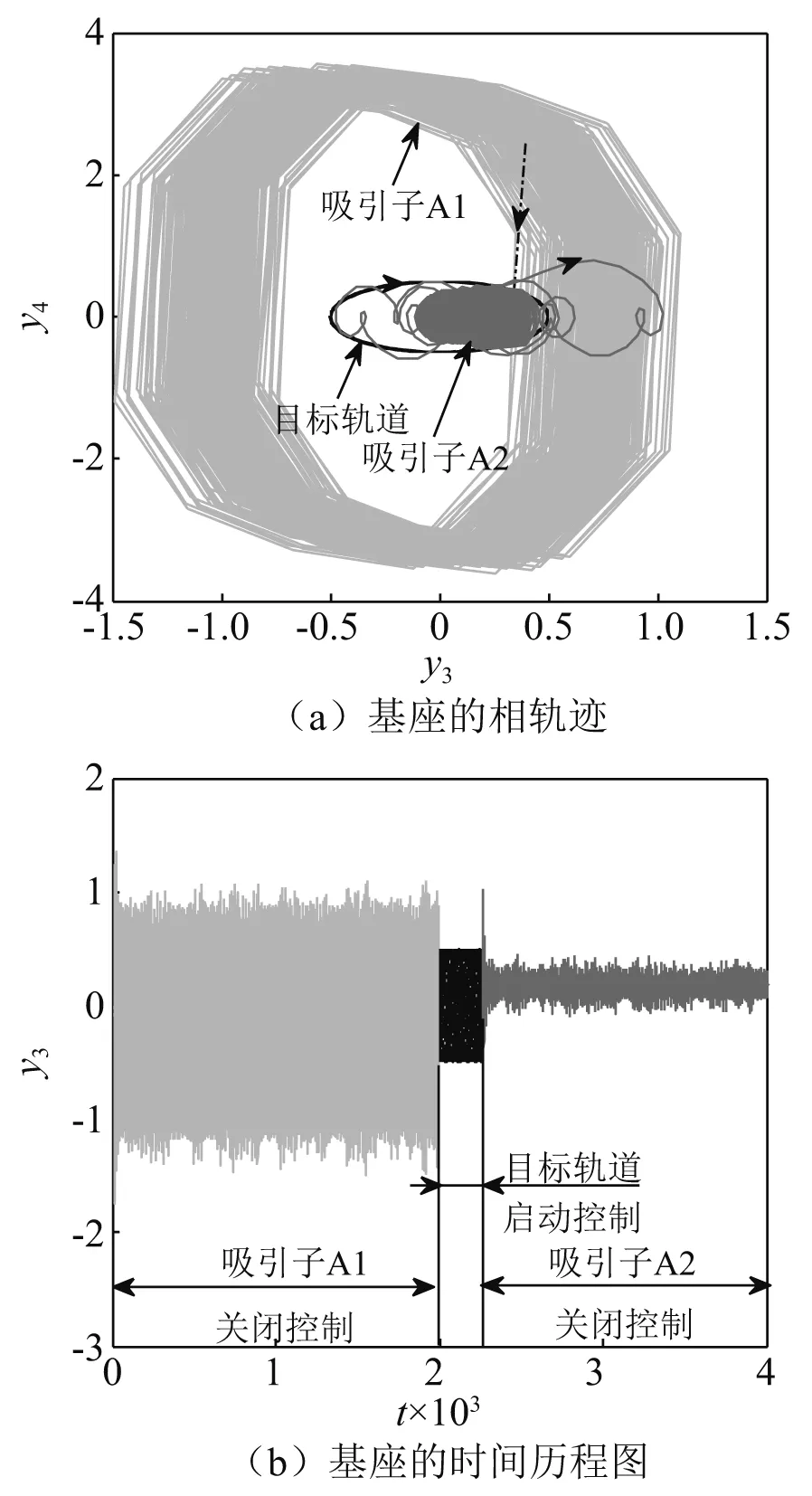
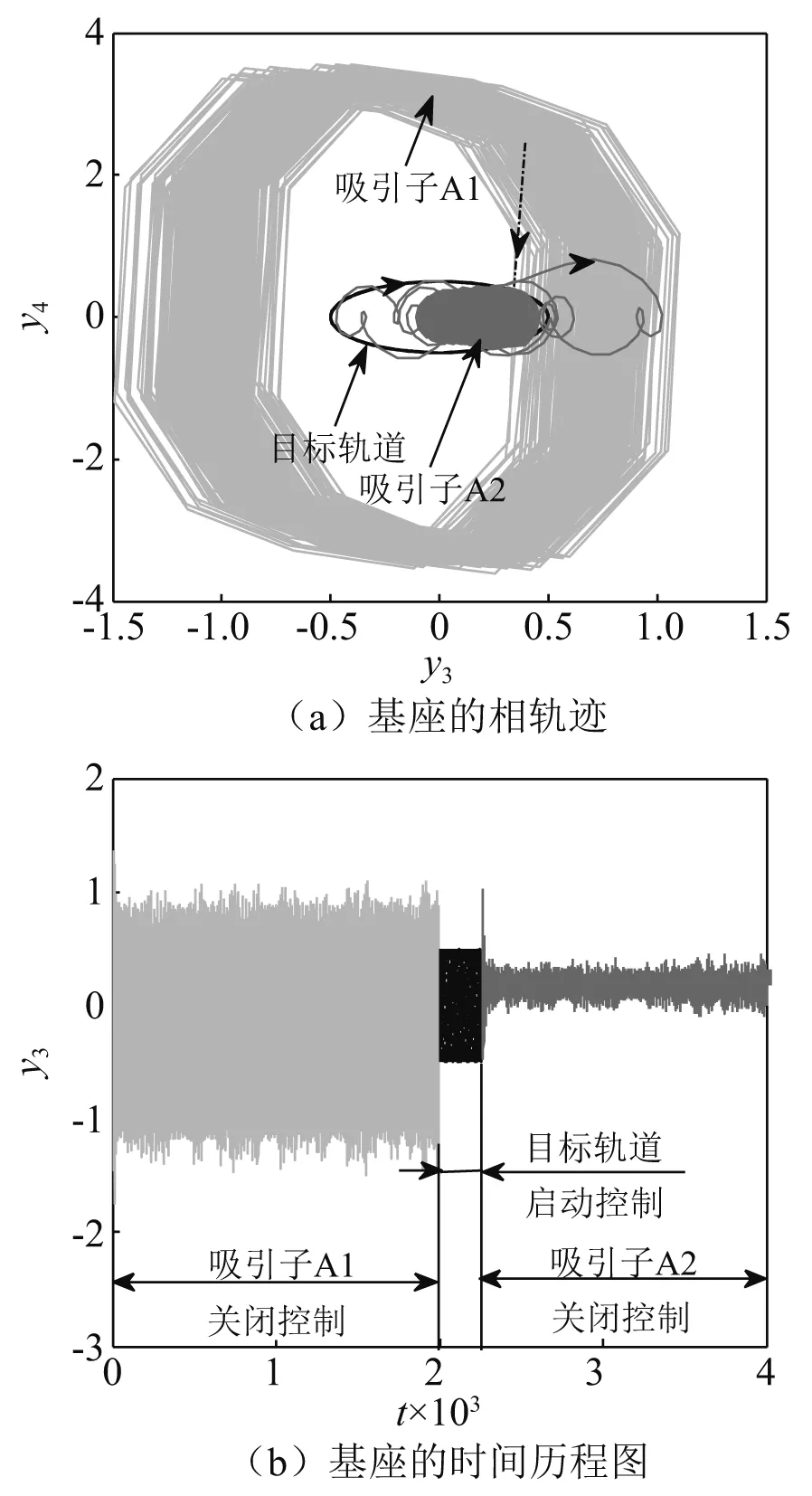
4 稳定性分析
5 结 论
