基于储备池计算的电机系统混沌预测与同步研究

陈豪昌,韦笃取

(广西师范大学 电子工程学院,广西 桂林 541004)

最近的研究表明电机系统在某些参数及工作条件下会出现的混沌振荡，是电机运行失稳的重要因素之一[1-2]。因此研究电机系统混沌预测，为及早提出保护措施,确保电机系统稳定运行具有重要意义。目前，非线性系统的混沌预测主要利用相图法、关联维数法及最大Lyapunov指数法等基于相空间重构的混沌判定方法[3-4],其前提是进行相空间重构。而相空间重构的效果取决于嵌入维数和延迟时间的选取,这两个参数一般靠人工经验设计，计算比较复杂,影响预测的准确性。若能找到一种既减轻人工参与的繁琐工作,又能自动学习到信号重要本质特征的方法,将对非线性系统的混沌预测具有重大意义。

人工神经网络由于具有对任何非线性函数的逼近能力、自学习能力、快速优化计算能力以及较强的容错性等优点而被广泛应用于信号预测[5-7]、电力负荷预测[8-9]、天气预测[10]等多种实际场合。最近的研究进展已经表明了一种称为储备池计算的机器学习方法对无模型混沌系统预测的有效性[11-13],其起源于两篇论文中提出的一个想法[14-15]。在该方法中,具有大量内部节点储层由一个与时间相关的信号驱动；内部变量之间的连接是随机选择的,然后保持固定；储备池计算的输出是单个节点,其状态由内部变量线性组合决定。线性组合的权重通过训练以使输出尽可能接近所需目标。储备池计算实际上是一种新的递归神经网络(也被称为回声状态网络)的训练方法，其预测原理是,储备池首先由非线性动力系统的状态训练并预测未来下一步的状态,训练结束后循环并将储备池的输出反馈回自身,因此它将发展成能接近原来动力系统的自治系统[16-17]。本文以永磁同步电动机(permanent magnet synchronous motor,PMSM)为例,基于储备池计算的机器学习方法对电机混沌行为进行预测，发现一个训练好的神经网络，即使在未知电机系统方程的情况下，也能预测电机系统的混沌行为，并且只需要通过一个状态变量的时间序列就能够实现受训神经网络与电机系统之间的混沌同步。

1 储备池计算模型

储备池计算属于递归神经网络的训练方法，其网络分为输入层、隐藏层和输出层。其中隐藏层也叫储备池，含有个内部神经元,储备池的状态向量r∈RNr，更新方程定义[18]为

r(t)=(1-a)r(t-1)+atanh[Ar(t-1)+Win(1;x(t))]

(1)

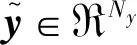
(2)

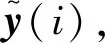
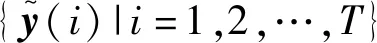
(3)

为了最小化损失函数，Wout训练根据岭回归进行，由式(4)计算得出

Wout=YtargetXT(XXT+λI)-1

(4)

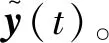
标准化处理在许多预测任务中得到广泛使用，主要目的是加速训练网络，为了防止网络在训练过程中出现的内部协变量转移，很大程度减轻网络过拟合的问题：对于大小为m的输入数据x，计算数据的均值μ和方差s2，对输入数据进行标准化处理

(5)

(6)

(7)

(8)

标准化处理和重建让网络可以学习到不同数据间的相对误差，使得对损失函数权重影响保持一致。让储备池模型有更好的范化性和收敛效果。

对于不同参数的组合,就会得到不同的储备池模型,产生不同的网络权重。把模型在测试集进行评估，通过多次试验验证其均方误差，取得更加准确评估，得到的储备池模型性能优越的参数见表1。

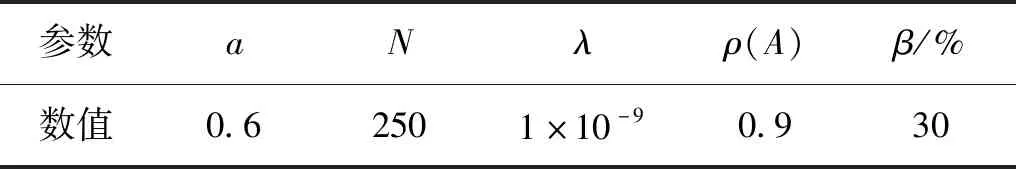
表1 储备池模型参数Tab.1 Parameters of reservoir computing

2 PMSM系统模型与试验仿真

本文采用均匀气隙永磁同步电动机为研究对象,其无量纲数学模型可表示为[19]

(9)

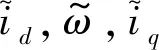
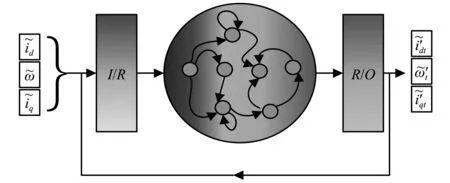
图1 全部状态变量作为储备池网络驱动输入的流程示意图Fig.1 Schematic illustration of reservoir computing used all of state variables as driving inputs

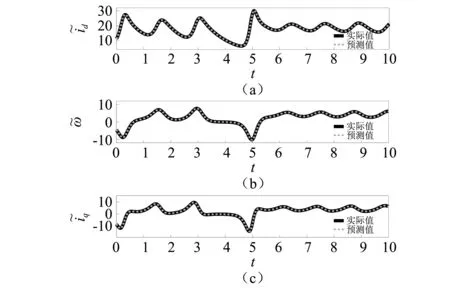
图2 储备池计算方法对PMSM变量的预测输出Fig.2 Predicted output of reservoir computing for variable

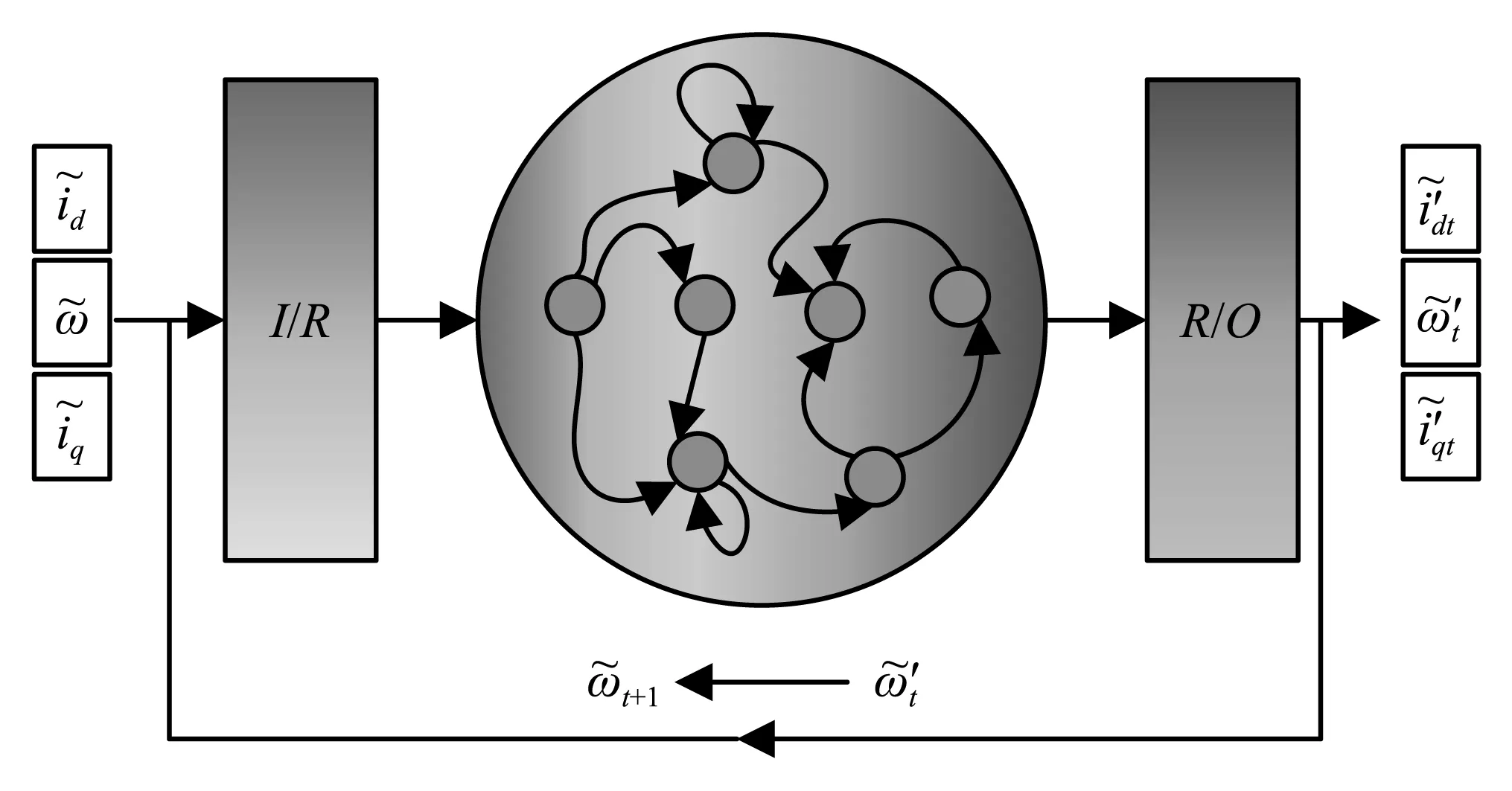
图3 单变量作为储备池网络驱动输入的流程示意图Fig.3 Schematic illustration of reservoir computing used univariate as driving inputs

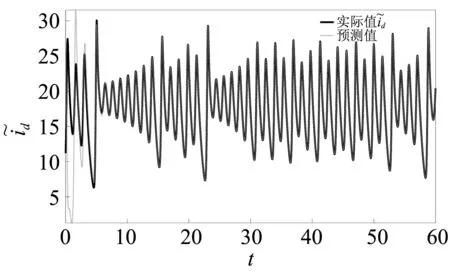
图4 达到混沌同步的状态变量Fig.4 Synchronization of trained reservoir computers for state variable

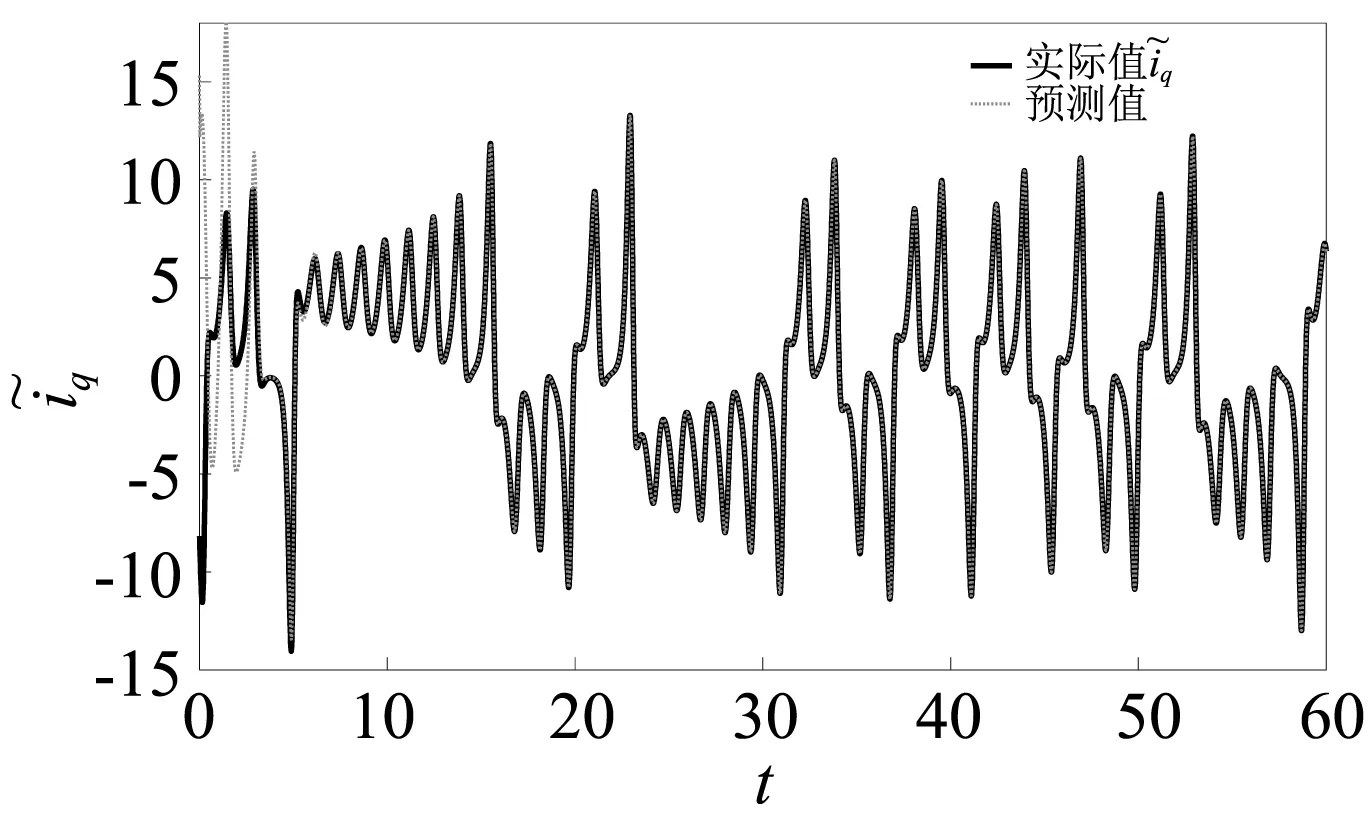
图5 达到混沌同步的状态变量Fig.5 Synchronization of trained reservoir computers for state variable

图6 电机系统状态变量的实际值与储备池预测的响应状态变量之间的误差曲线Fig.6 The error between actual value and the response state variable predicted by reservoir computing

3 鲁棒性研究

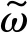
图7 状态变量的实际值与受扰动后的预测值曲线图(噪声在t=0时加入) Fig.7 The actual value and the predicted value adding noise disturbance at t=0

图8 状态变量的实际值与受扰动后的预测值曲线图(噪声在t=0时加入)Fig.8 The actual value and the predicted value adding noise disturbance at t=0

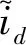
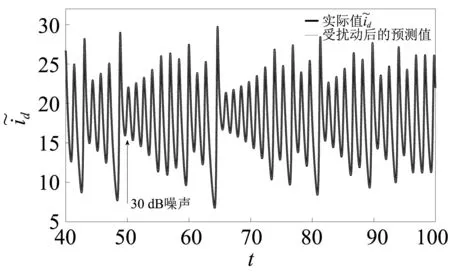
图9 状态变量的实际值与受扰动后的预测值曲线图(噪声在t=50 s时加入)Fig.9 The actual value and the predicted value adding noise disturbance at t=50 s

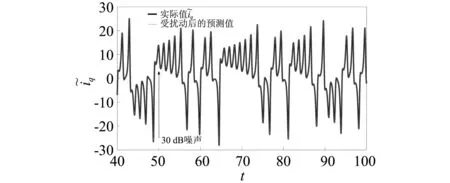
图10 状态变量的实际值与受扰动后的预测值曲线图(噪声在t=50 s时加入) Fig.10 The actual value adding noise disturbance at t=50 s

4 结 论

本文基于储备池计算网络的机器学习技术,研究电机系统混沌预测,并以PMSM为例进行了数值仿真.实验结果表明,只需通过用电机系统状态变量的时间序列数据对储备池计算网络的训练，就能实现电机系统的混沌预测,并且只需要通过一个状态变量就能够实现受训神经网络与电机系统之间的混沌同步。此外，本文还分析了储备池计算方法的鲁棒性，结果表明无论扰动是发生在储备池算法的预测开始，亦或者中途，储备池计算网络都能够在很快的时间段进行混沌预测，即该方法对外界环境扰动具有鲁棒性，因此确保了预测模型对电机系统预测的稳定性,为电机系统的混沌预测与同步提供了一种新方法。