混合弹流润滑下内啮合直齿轮动态特性磨损退化研究
2021-09-27宁志远陈长征
宁志远 ,陈长征
(沈阳工业大学 机械工程学院,沈阳 110870)
1 数学模型
1.1 黏着磨损
黏着磨损计算首先是由Archard提出,计算公式[13]为
(1)
式中:V为磨损体积;s为滑动距离;K为无量纲磨损系数;H为较软接触表面硬度;Ft为接触表面载荷。
在干摩擦,混合或边界润滑的表面上的P点处的黏着磨损通常可被视为从初值逐渐演变的过程并且由微分方程描述为
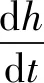
(2)
式中:h为磨损深度;k为磨损系数;p为接触点所受的压强;v为接触面相对滑移速度;t为时间。通过对t进行积分得到P点的磨损深度表示为
(3)
在对齿轮轻度磨损的研究中,可以将齿轮齿廓表面分成若干个微元,并且在该微元内的磨损假定为稳态,则可以通过简化计算得出各个微元内的磨损深度为
hi,j=hi,j-1+kpi,j-1vjΔt
(4)
式中:i为P点所在的单元;j为在点P的磨损次数;Δt为时间步长,磨损过程如图1所示。

图1 内齿轮磨损过程Fig.1 Internal gear wear process
图中:v1,v2分别为外、内齿轮在齿轮表面在啮合方向上的运动速度;P1P2为齿轮啮合线;点P为齿轮啮合点;s为时间步长Δt内齿轮表面的相对滑移距离;hP为齿轮在啮合点P处的磨损深度。
1.2 内齿轮动力学模型
本文以内啮合直齿轮为研究对象,建立2个自由度的动力学模型,分别为内外齿轮的角位移θ1和θ2,具体如图2所示。其中:Rb1,Rb2分别为外、内齿轮基圆半径;T1,T2分别为输入、输出力矩;I1,I2分别为外、内齿轮转动惯量;m1,m2分别为外、内齿轮的质量;Ke(t)为齿轮时变啮合刚度;c(t)为时变啮合阻尼;e(t)为齿轮齿廓误差。
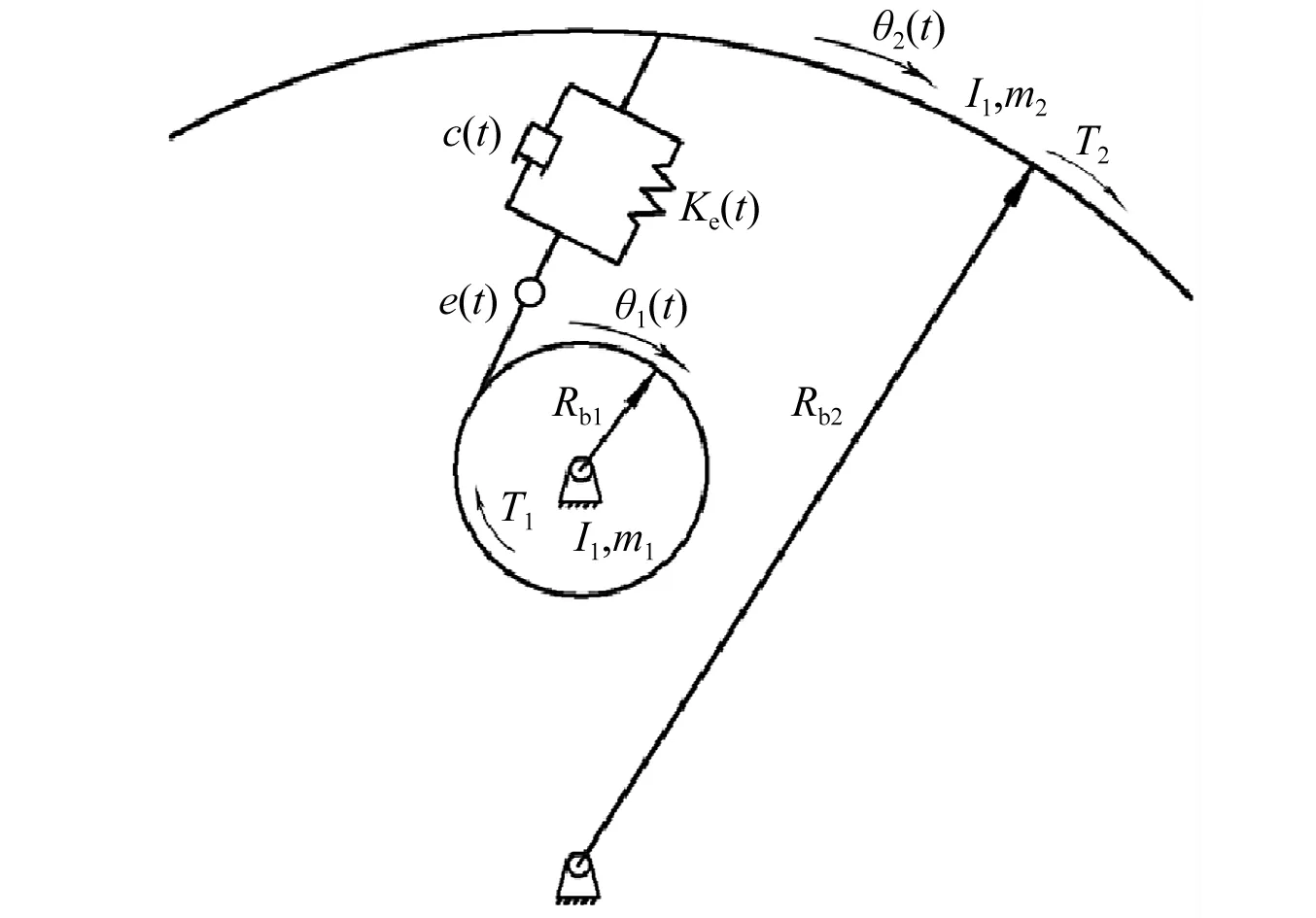
图2 内啮合直齿轮动态啮合模型Fig.2 Dynamic meshing model of internal meshing spur gear
由图2可以得到内啮齿轮啮合动力学方程为
(5)
式中:nz为参与啮合的齿对数;F为啮合齿对的啮合力;Λ为摩擦参数表示摩擦力方向,取值为±1;ρ为接触点圆弧半径;μ为摩擦因数。为求解动态啮合力,将角位移θ1和θ2转化为啮合方向的线位移y1,y2。假定Ft为外部载荷力,则可得到[14]
(6)
式中,S1i=ρ1i/Rb1,S2i=ρ2i/Rb2分别为外、内齿轮啮合点处曲率半径与其基圆半径之比。对于任意啮合齿对的动态啮合力可以表示为
Fi=Kei(yr-e)
(7)
式中,yr为齿轮齿向相对运动,yr=y1-y2,并且当yr-e<0时齿轮啮合点处的啮合力为Fi=0,当yr-e>0时,Fi>0。将式(7)代入式(6)整理后可得
(8)
将黏性阻尼考虑进去整理后可得
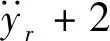
(9)
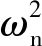
(10)
(11)
1.3 时变啮合刚度模型
弹性流体动压润滑分为3种润滑状态,通常采用膜厚比λ来判断接触表面润滑状态大部分齿轮传动工作在膜厚比λ=0.5~1.5。在该润滑条件下齿轮啮合刚度模型为并联模型,如图3所示。
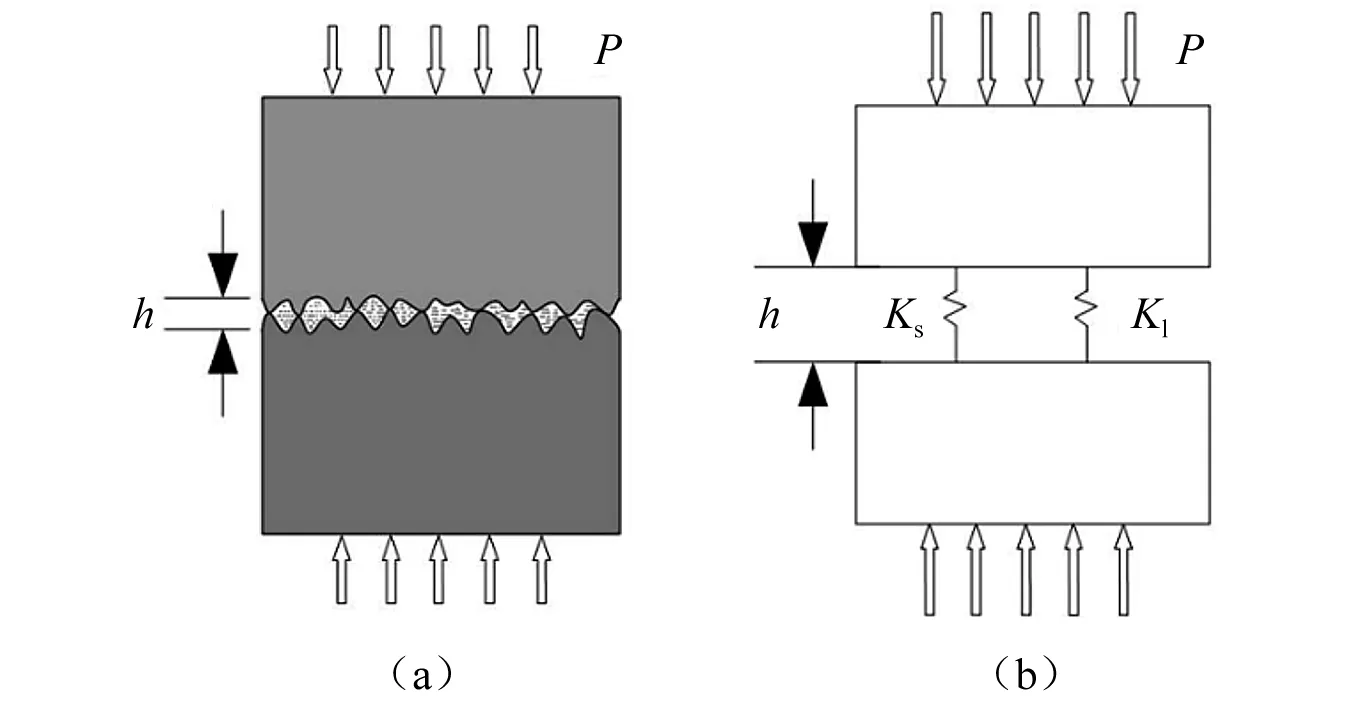
图3 轮齿接触刚度模型Fig.3 Gear tooth contact stiffness model
从图3并联模型中可以看出,啮合刚度由齿面时变啮合刚度Ks和油膜时变刚度接触刚度Kl共同组成[16]。然而在混合润滑条件下齿面与油膜各自的承载比例会随着动态载荷的变化而变化,为准确描述综合啮合刚度Ke,将承载系数引入并联模型中,用以描述在干摩擦与油润滑摩擦之间的状态。1/γ1和1/γ2分别为油膜和齿面承载系数,并且1/γ1+1/γ2=1可以通过粗糙峰变形公式进行确定。当接触为干摩擦时,1/γ2=1即油膜承载系数为0,当接触为油润滑时,1/γ1=1即齿面承载系数为0。此时可以认为齿轮啮合综合刚度Ke可通过如下关系得到
Ke=K1/γ1+Ks/γ2
(12)
式中,Ks表达式[17]为
Ks=K1K2KH/(K1+K2+KH)=Ks(ξ)
(13)
式中:K1为内齿轮刚度;K2为外齿轮刚度;KH为接触刚度;ξ为P点接触参数。轮齿刚度Ki在P点的啮合刚度根据最小势能原理,可以表示为
Ki=(1/kix+1/kis+1/kin)-1
(14)
式中:kix为第i齿对的齿轮弯曲刚度;kis为第i齿对的轴向拉压刚度;kin为第i齿对的扭转剪切刚度,可分别表示为
(15)
式中:αP为P点压力角;γP为P点接触角厚度;G为剪切弹性模量;et(y)为y对应的齿轮截面齿厚;yb和yp分别为根截面和载荷截面对应的值;Cs为当量修正系数,这里取值为Cs=1.5[18]。
为求解油膜刚度公式可以根据弹流动压公式中对油膜刚度的定义式算得到[19]
(16)
式中:F1为接触区的油膜承载载荷可通过式(23)进行计算;h1为油膜中心位移;δ∞为接触区稳态下油膜的压缩变形,δ∞=-h1。
根据弹流润滑建立无量纲油膜润滑方程。首先将油膜变形进行无量纲化,得到无量纲油膜形变Δ∞,其定义式为
Δ∞=δ∞/c
(17)
式中,c为赫兹接触变形,其表达式为
(18)
式中:E′为综合弹性模量;RP为P点综合曲率半径。无量纲油膜形变Δ∞表达式为[20]
Δ∞(M,L)=1-p(L)Mq(L)
(19)
式中:M为无量纲载荷参数;L为无量纲润滑参数;p(L),q(L)均为无量纲润滑参数L的函数。
为求解油膜刚度,需要首先将无量纲油膜形变Δ∞转化为δ∞关于w的函数,通过将式(17)和式(19)联立后将得到
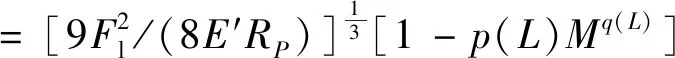
(20)
根据定义式(16)对式(20)中的δ∞求导可得到油膜刚度。
1.4 摩擦力矩与承载系数
内啮合齿轮摩擦因数μ的定义式为
μ=Ft/Ff
(21)
式中,Ff为总摩擦力。在混合弹流润滑条件下,齿轮接触处的摩擦力由油膜和齿面粗糙峰共同承担。总的接触载荷为Ft表达式为
(22)
式中:Fl为油膜承载力;Fs为齿承载力,因此总摩擦力Ff=Ffl+Ffs,其中Ffl为油膜摩擦力
Ffl=∬A0τsdA
(23)
式中:τs为油膜剪切应力;A为赫兹接触面积。同时,Ffs为齿面摩擦力
Ffs=fsFs
(24)
式中,fs为摩擦因数,这里取0.1。油膜与齿面承载系数1/γ1和1/γ2可以通过粗糙峰受力方程计算[21]
(σs/R)-0.418 941W0.39)-1.690 59]-0.591 5=
(25)
式中,各参数和函数可参照Wijnant研究中的参数定义及其计算公式进行确定。
2 数值求解
为描述齿轮动态磨损过程,将齿轮从齿廓渐开线与基圆的交点定为初始点,时间t记为0,在轮齿进入啮合的时间记为t1,退出啮合点的时间记为t2,进入单齿啮合区的时间记为ta,退出单齿啮合区的点记为tb;将齿轮从进入啮合时间t1到退出啮合时间t2等间距分割成100个时间步长。具体如下图4所示。
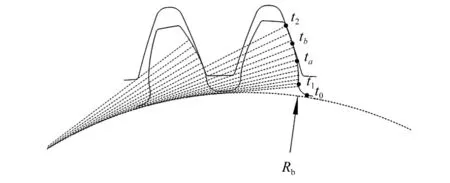
图4 齿轮啮合各时间点Fig.4 Gears at various points in time
由于承载系数与啮合力之间相互耦合,则需先求出初始啮合力。同样可以利用最小势能法,计算齿轮初始载荷分配比[22]
(26)
式中:Ri为任一啮合齿对的载荷分配比;ξ为啮合参数与啮合时间t呈正相关。初始啮合力Fd0为
Fd0=Ri(ξ)Ft
(27)
将初始啮合力Fd0作为迭代初值,代入式(31)求解出齿轮载荷系数1/γ1,1/γ2和分配载荷Fs,Fl,用于求解综合接触刚度,进而可以通过式(10)求解得出齿轮动态啮合力Fd1,通过调整得到新的迭代初值。经过多次迭代后将得到的齿面动态啮合力代入齿面磨损模型中,可求解出齿面磨损分布。
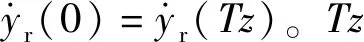
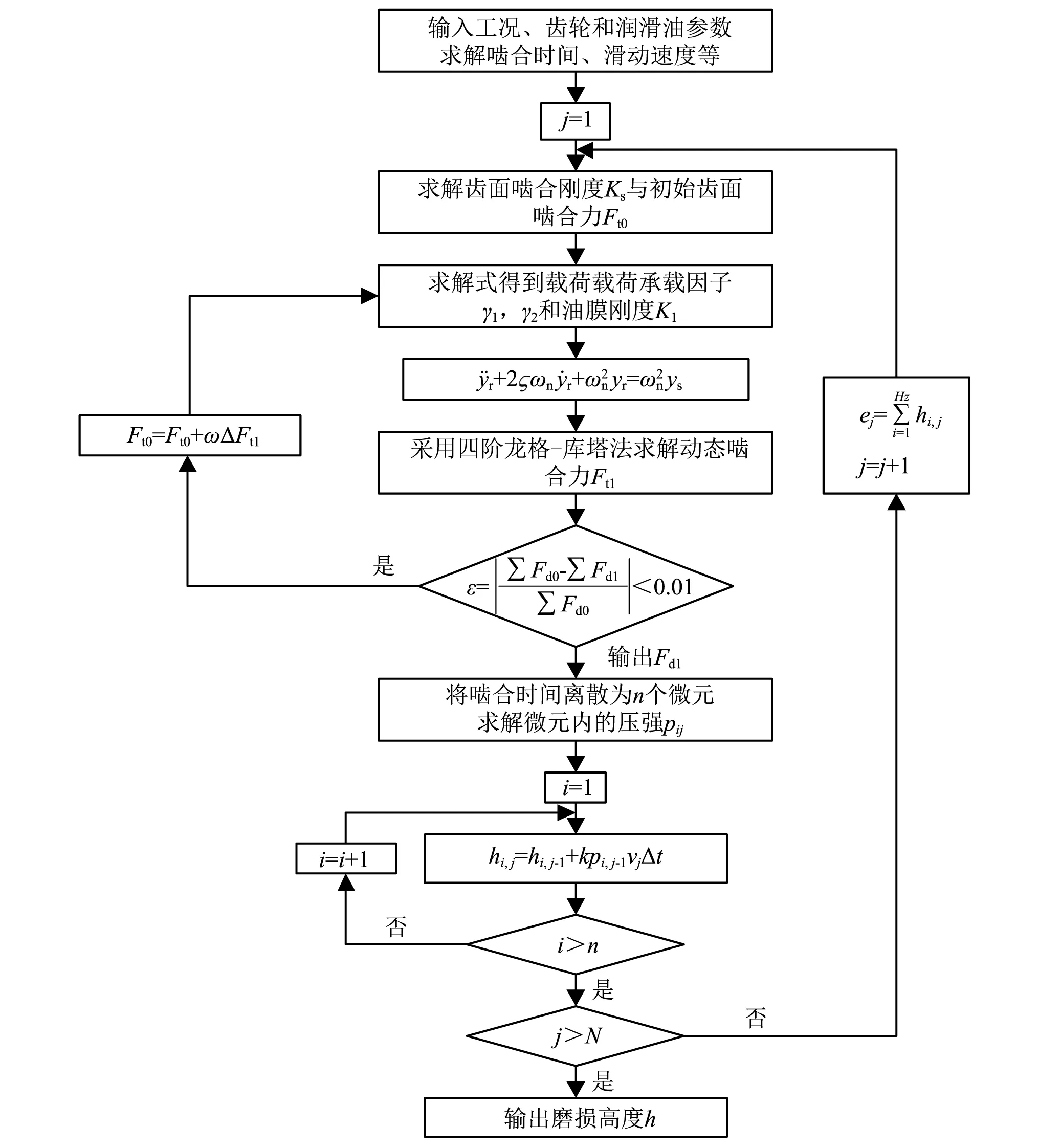
图5 求解流程Fig.5 Solving process
表1中给出了齿轮尺寸参数,并以表中参数为例进行计算,讨论了内啮合齿轮的动态啮合刚度Ke(包括齿面刚度Ks和油膜刚度Kl)的变化,以及在考虑动态啮合刚度是齿轮的动态啮合力Fd1沿齿面分布的变化。同时,研究了在动态载荷Fd1条件下其随内啮合齿轮表面磨损量h分布,以及磨损后动态载荷Fd1和动态承载系数1/γ1和1/γ2的影响。

表1 齿轮参数表Tab.1 Gear parameter table
3 结果分析
3.1 齿面磨损结果对比分析
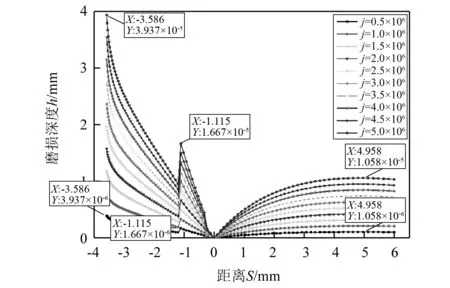
图等计算的内齿轮j次啮合后动态磨损分布j=(0.5,1.0,…,5.0)×106Fig.6 et al.calculated the dynamic wear distribution of the internal gear after j times of meshing j=(0.5,1.0,…,5.0)×106
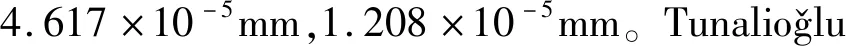
图等计算的外齿轮j次啮合后动态磨损分布j=(0.5,1.0,…,5.0)×106Fig.7 et al.calculated the dynamic wear distribution of the external gear after j times of meshing j=(0.5,1.0,…,5.0)×106
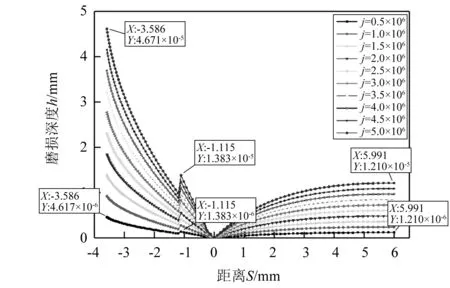
图8、图9分别为内、外齿轮在上述转速下经历过j=(0.5,1.0,…,5.0)×106次啮合后的齿轮磨损分布。图8中内齿轮在j=0.5×106和j=5.0×106时磨损分布均有4个峰值点。在j=0.5×106时,内齿轮磨损厚度峰值点横坐标分别为-3.586 mm,-3.208 mm,-2.090 mm和1.935 mm。在j=5.0×106时,峰值点横坐标分别为-3.550 mm,-2.779 mm,-1.868 mm和2.208 mm。外齿轮在j=0.5×106和j=5.0×106时的磨损厚度峰值横坐标分别为,-2.090 mm,1.930 mm和-1.791 mm,2.208 mm。内、外齿轮的磨损厚度峰值点均向退出啮合点有所移动。同时在峰值点的磨损厚度与啮合次数之间呈非线性关系,并且没有磨损突变的情况,进入段的磨损量明显大于退出段的磨损量,这与文献[23]中的试验结果一致。该现象是由于磨损受到齿面冲击的影响,使得齿面磨损显示出非线性分布的特征。
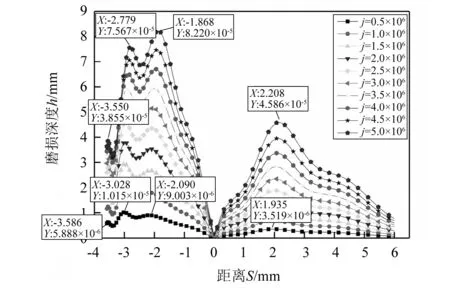
图8 内齿轮j次啮合后动态磨损分布j=(0.5,1.0,…,5.0)×106Fig.8 Dynamic wear distribution of internal gear after j times meshing j=(0.5,1.0,…,5.0)×106
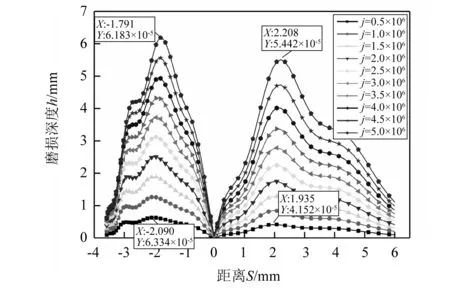
图9 外齿轮j次啮合后动态磨损分布j=(0.5,1.0,…,5.0)×106Fig.9 Dynamic wear distribution of internal gear after j times meshing j=(0.5,1.0,…,5.0)×106
3.2 齿轮啮合动态性能退化分析
齿面磨损量很小,计算得到的齿面相对滑动速度的影响可以忽略,因此这里仅分析齿面载荷随磨损的变化。
图10中给出了Fd0随啮合周期t的分布。通过载荷分配比R(ξ)得到齿轮啮合静态啮合力Fd0。静态啮合力作为迭代计算初值,在动态条件下的齿轮啮合力的变化也是产生齿轮动态磨损与静态磨损的区别的原因。同时,齿轮动态啮合力也会随着磨损的增加发生变化。
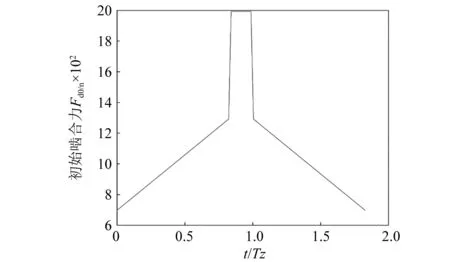
图10 静态啮合力Fd0Fig.10 Static meshing force Fd0
图11中给出了在j次啮合后的动态啮合力的变化趋势。图11中动态啮合力相较于静态啮合力而言较为平滑,没有了啮合力的突变,且呈现双峰分布,分别为1.005Tz和1.298Tz处。随着磨损增加后在0.768Tz处会逐渐出现新的峰值。在1.298Tz处的峰值从1 264 N逐渐增大至1 740 N,增大了37.66%,并且峰值点横坐标会向右移动至1.371Tz处。而在j=0.5×106和j=5.0×106时的最大啮合力分别为2 236 N和2 193 N,随磨损增大减小了1.92%。
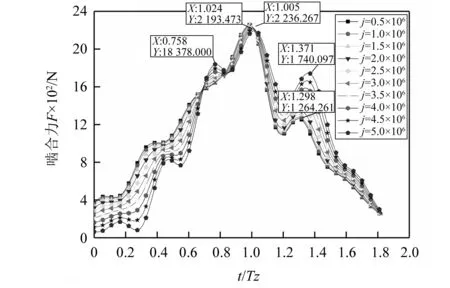
图11 在j次啮合后齿轮动态啮合力j=(0.5,1.0,…,5.0)×106Fig.11 Dynamic meshing force of gears after j mesh times j=(0.5,1.0,…,5.0)×106
图12中为描述啮合力增量随啮合次数的变化,以j=0.5×106次啮合后得到的动态啮合力为基准动态啮合力,将j=(0.5,1.0,…,5.0)×106时的动态啮合力减去基准啮合力得到啮合力增量分布。动态啮合力增量共有6个峰值,对应横坐标分别为0.036 56Tz,0.310 80Tz,0.585 00Tz,0.914 10Tz,1.261 00Tz和1.591 00Tz,意味着随着齿轮不断磨损,动态啮合力将出现6个峰值点,齿面冲击逐渐加剧。磨损后的啮合力增量呈现逐渐收敛的趋势。
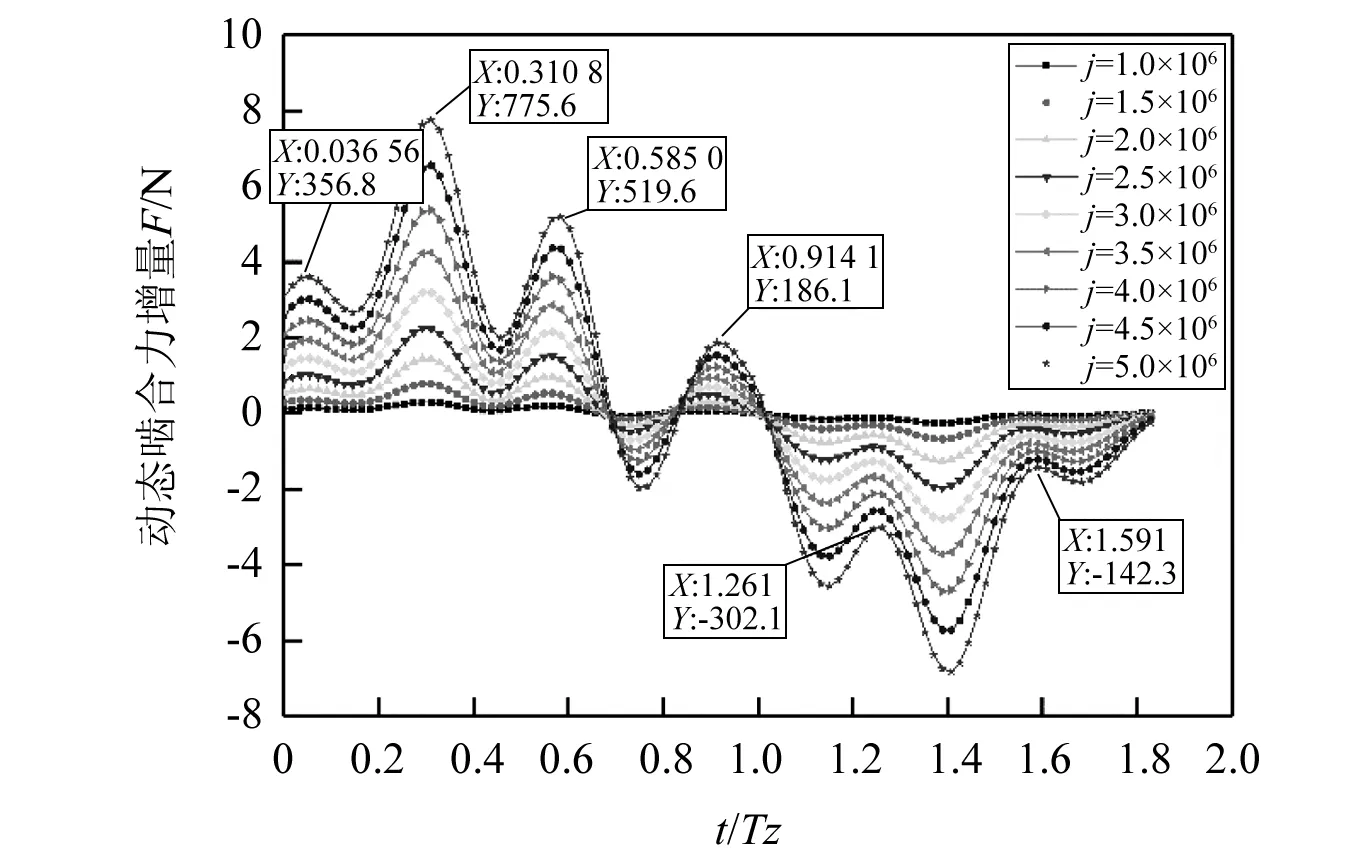
图12 在j次啮合后动态啮合力增量分布j=(0.5,1.0,…,5.0)×106Fig.12 Dynamic meshing force increment distribution after j mesh times j=(0.5,1.0,…,5.0)×106
从图13中可以看出,在j=0.5×106时齿向相对位移最大值在0.987 2Tz处为0.002 355 mm,最小值在1.188 0Tz处为0.001 222 mm。随着磨损增加,最大值则对应两个横坐标分别为0.400 2Tz和1.389 0Tz,并增加至0.002 823 mm,最小值在1.188 0Tz处为0.001 749 mm。分别增加了19.87%和43.12%。从图14中可以看出在j=0.5×106时齿向相对速度最大值在0.895 8Tz处为0.336 9 mm/s,最小值在1.079Tz处为-0.670 7 mm/s。在j=5.0×106时最大值在1.298 0Tz处为0.592 8 mm/s,最小值在1.463Tz处为-0.436 4 mm/s,分别增加了78.99%和34.93%。齿向相对位移和相对速度的振幅分别增大了-5.21%和2.72%同时在在j=0.5×106时0.822 7Tz处有明显的冲击,随着磨损增大,冲击逐渐消失。随着磨损增大,在单双齿交替点处齿轮振动的相对位移和相对速度振幅变化不大,振动周期逐渐缩短,高频振动增加,齿轮啮合条件逐渐恶化。
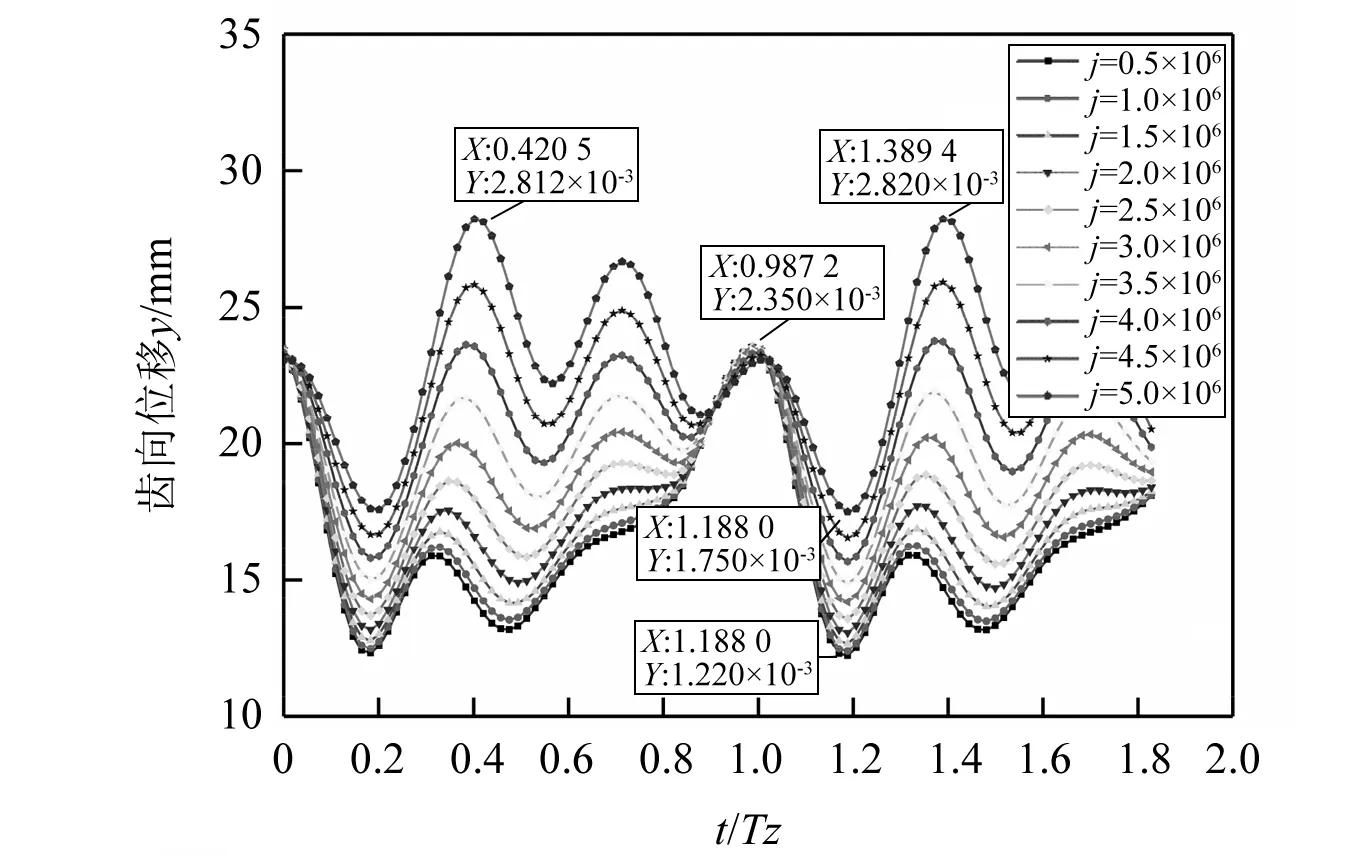
图13 在j次啮合后啮合相对位移分量j=(0.5,1.0,…,5.0)×106Fig.13 Displacement component of mesh line after j mesh times j=(0.5,1.0,…,5.0)×106
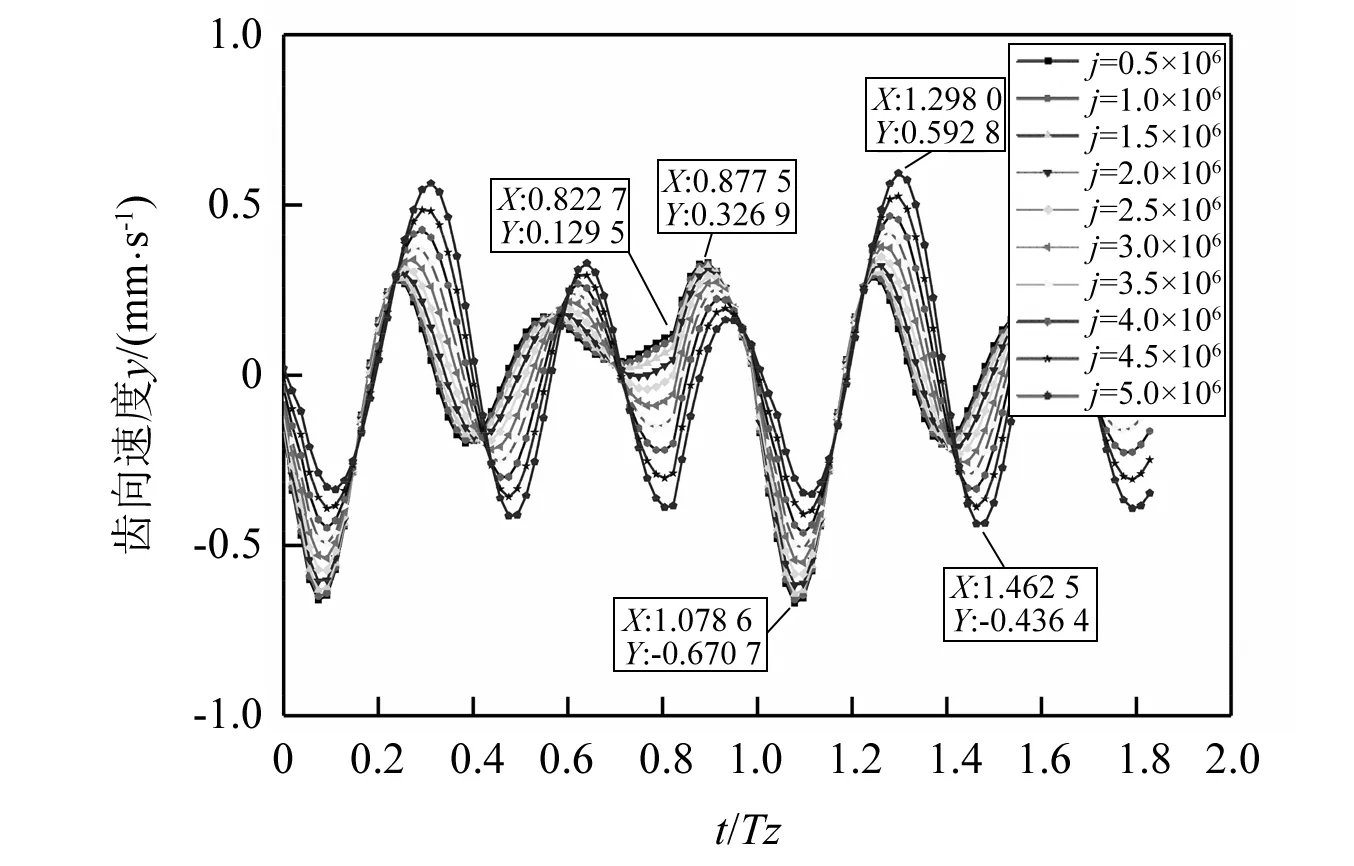
图14 在j次啮合后啮合线速度分量j=(0.5,1.0,…,5.0)×106Fig.14 Velocity component of mesh line after j mesh times j=(0.5,1.0,…,5.0)×106
3.3 齿轮啮合刚度退化分析
在冯松等[24]的研究中发现,在齿轮的正常均匀磨损对齿轮齿对的啮合刚度影响有限,因此本文中忽略了磨损对齿轮齿面刚度Ks的影响,图15中为齿面刚度Ks随时间t的变化。
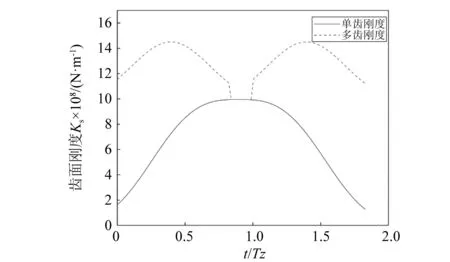
图15 齿轮齿面刚度Ks随时间变化趋势Fig.15 Variation trend of stiffness Ks of gear tooth surface with time
为分析磨损量对油膜刚度Kl的影响,分别采用文献[25]和本文的计算方法,计算了动载荷条件下j次啮合后的齿轮油膜刚度Kl。
从图16中可以看出同样在齿面磨损量不断增加的条件下,肖泽亮的计算方法得到的稳态载荷下的油膜刚度Kl曲线基本不会发生变化,没有表现出啮合的动态特征。而本文中的计算方法得到的Kl曲线却有明显分离的现象。在j=0.5×106和j=5.0×106时油膜刚度为双峰分布,横坐标分别为1.005 0Tz,1.316 0Tz和1.060 0Tz,1.389 0Tz,对应的油膜刚度大小分别为1.776×108N/m,1.730×108N/m和1.797×108N/m,1.962×108N/m。在左峰值点油膜刚度增大了1.18%,右峰值点油膜刚度增大了13.41%。结合前文分析可以认为,油膜刚度的变化主要是由于退出段齿轮动态啮合力Fd1导致的。两种计算方法得到的计算结果均表明进入段的油膜刚度要明显小于退出段的油膜刚度。
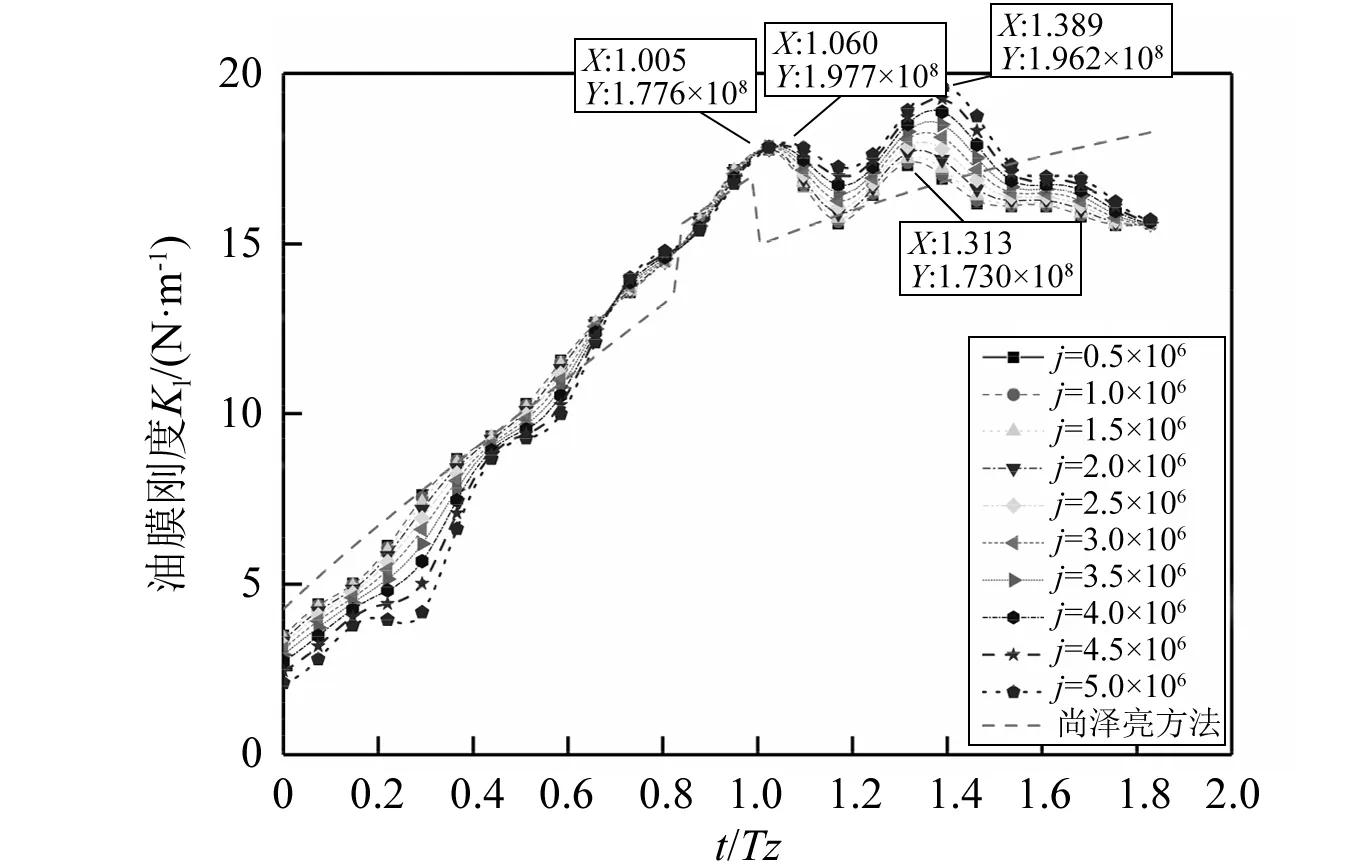
图16 j次啮合后齿面油膜刚度Klj=(0.5,1.0,…,5.0)×106Fig.16 Oil film stiffness of the tooth surface after j mesh times j=(0.5,1.0,…,5.0)×106
油膜刚度对于齿轮磨损较为敏感,然而决定综合刚度Ke的变化还取决于承载系数1/γ1和1/γ2,图17中给出了不同啮合次数下承载系数1/γ1和1/γ2时随时间的变化规律。从图17中可以观察到的1/γ1和1/γ2在退出段有明显的分离,随着磨损的增大,油膜承载系数在退出段会有所减小。同时在j=5.0×106时在进入段油膜承载系数会产生突变,说明此时油膜的稳定性有所下降。但是由于油膜承载系数较小,使得油膜刚度对于综合刚度贡献较小,导致综合刚度对磨损量变化不敏感。
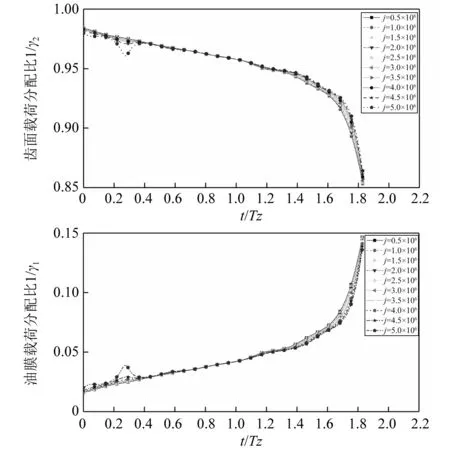
图17 j次啮合后承载系数1/γ1和1/γ2的变化趋势j=(0.5,1.0,…,5.0)×106Fig.17 Variation trend of bearing coefficient and after j mesh times j=(0.5,1.0,…,5.0)×106
图18给出不同磨损量下的齿轮综合啮合刚度Ke。图中的多条曲线并没有产生分离,说明齿轮磨损对综合刚度Ke基本没有影响。
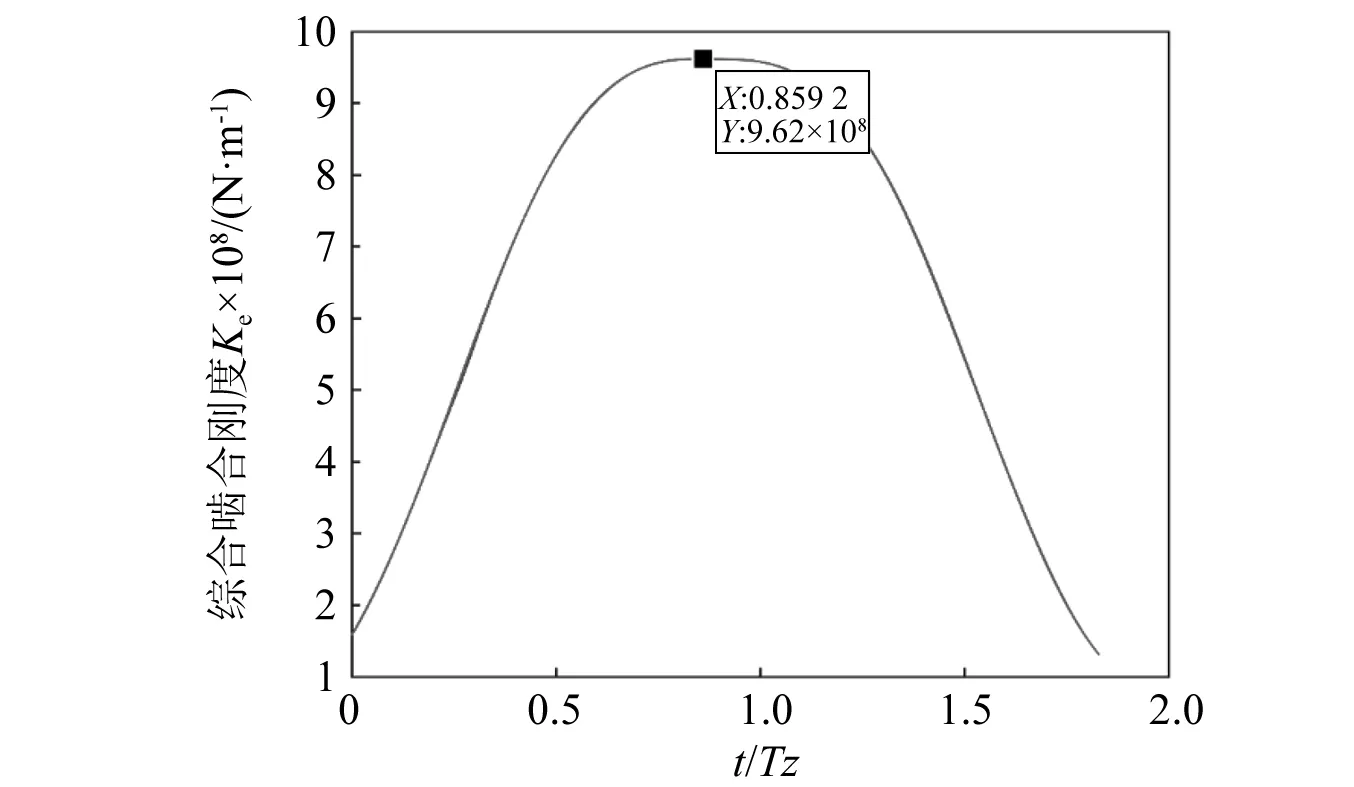
图18 j次啮合后的综合刚度K分布j=(0.5,1.0,…,5.0)×106Fig.18 Distribution of comprehensive stiffness K after j mesh times j=(0.5,1.0,…,5.0)×106
4 结 论
(1)通过齿面磨损计算结果可以发现,在动态磨损过程中,进入段磨损大于退出段的磨损。随着啮合次数的增加,内、外齿轮的磨损峰值点会向退出啮合点偏移,并且在进入段的磨损逐渐减弱,在退出段的磨损逐渐增强,呈非线性特征。
(2)通过齿轮动态特性可以看出,随着啮合次数增大,齿轮啮合力呈多峰分布,齿向最大相对位移、相对速度增幅分为19.887%和78.99%,振动频率逐渐增大,内啮合齿轮啮合条件逐渐恶化;但是动态啮合力增量逐渐收敛,齿轮齿向速度冲击点逐渐消失,磨损可以改善内啮合直齿轮齿面冲击。
(3)通过不同啮合次数下的油膜刚度可以看出,随着啮合次数增加,油膜刚度在进入段逐渐减小,在退出段逐渐增加,峰值分别增加1.18%和13.41%,而综合啮合刚度无明显变化,油膜刚度对齿轮动力学特性影响较小。
(4)退出段油膜承载系数增大,可以有效抑制退出段的齿面磨损,从而抑制齿轮均载水平的下降,并且在啮合次数较少时,磨损对承载系数影响有限,在啮合次数较多时,承载系数发生突变,油膜稳定性下降。本文对齿轮磨损后动力学模型的退化研究对齿轮磨损与寿命预测有指导和参考价值。
