黏弹性耗能结构系统非均匀和完全非平稳响应的精细积分格式

李创第，王博文，昌明静

(广西科技大学 土木建筑工程学院，广西 柳州 545006)

在结构抗风抗震中，黏弹性阻尼器已得到广泛应用[1]。其中，Maxwell阻尼器模型具有本构方程简便、物理意义明确、易于扩阶分析、模型计算参数易于从试验数据拟合[2-3]等优点被广泛应用。一般黏弹性阻尼器、一般线性流体阻尼器、黏滞阻尼器都可用Maxwell阻尼器模型建模[4-5]，故研究Maxwell阻尼器耗能结构具有重要的理论和工程意义。

在减震结构系统中，阻尼器一般与支撑串联安装[6]，我国GB 50011—2010《建筑抗震设计规范》[7]通过控制支撑的最小刚度，使得串联安装系统达到或接近纯阻尼器的效果，所以结构系统响应分析要考虑支撑的影响[8]。由于地震发生会首先引起支撑、阻尼器等结构保护系统的破坏，进而导致结构体系的损伤甚至倒塌，目前相关规范明确要求耗能减震系统构件在结构设计基准期内应具备足够的变形、耗能能力和良好的抗震动力可靠度，故结构及结构保护系统响应方法的建立，对于结构及阻尼器构件抗震动力可靠度乃至抗震设计方法的研究具有非常重要的意义。

地震动的非平稳随机特性具有频率非平稳和强度非平稳的特点[9]，非平稳随机地震响应的分析比平稳随机地震响应的分析更加符合地震的随机特性，在实际工程中的应用更有价值，目前均匀调制随机激励的研究使大多数地震的非平稳随机响应分析局限于此，因此，非均匀非平稳和完全非平稳[10]随机地震激励的研究正日益受到广大科研人员的高度重视[11-13]。Conte等提出了可以由实际地震加速度演变功率谱经自适应最小二乘法拟合确定参数的完全非平稳模型，该模型同时反映了地震的强度非平稳和频率非平稳特性，其计算参数可通过实际地震加速度演变功率谱拟合得到，具有较强通用性。

针对结构响应的功率谱密度计算方法，林家浩等提[14-15]出了高效的虚拟激励法，将平稳和非平稳随机振动分别转化为简谐振动分析和确定性时间历程分析，在计算步骤简化的基础上仍保持理论上的高度精确性。该方法被广泛应用于结构动力响应、风工程、海洋工程、偏微分方程的求解等众多领域，但是目前关于设置支撑的黏弹性阻尼器耗能减震结构基于虚拟激励法的非平稳响应分析尚未建立。

钟万勰等[16-17]提出的精细积分法，对于计算机求解指数矩阵的精度有显著的提高，能有效的降低因精细划分所引起的误差，这种积分方法虽然不是提供解析解公式，但其数值计算结果却是高度准确的。目前林家浩等[18]提出了简谐、多项式简谐、指数简谐型精细积分格式，已应用于无阻尼器结构的均匀非平稳随机响应高效分析，但仅对于特定形式的激励效率较高，对于均匀与非均匀非平稳、完全非平稳响应的简谐-指数-多项式精细积分一般通用精确格式尚未建立。

本文为建立黏弹性耗能结构及其保护系统的抗震分析与设计方法，对设置支撑的Maxwell阻尼耗能系统随机地震响应的数值分析方法进行了系统研究。首先，采用设置支撑的Maxwell阻尼耗能系统进行建模；然后，基于高效的虚拟激励法，获得了均匀与非均匀非平稳、完全非平稳响应的简谐-指数-多项式精细积分一般通用精确格式，建立了8种经典调制非平稳和完全非平稳地震响应的精细积分精确格式；最后，可得Maxwell阻尼耗能系统的均匀与非均匀非平稳、完全非平稳地震响应方差，通过算例验证本文方法的正确性，为黏弹性阻尼耗能系统在均匀与非均匀非平稳、完全非平稳地震激励下的响应分析提供了方法。

1 结构运动方程

1.1 一般黏弹性阻尼器模型

一般积分型模型是黏弹性阻尼器中最一般的模型，能精确、简洁地描述其应力-应变关系，且计算结果较为准确。对于一般积分型阻尼器计算模型，如图1所示。

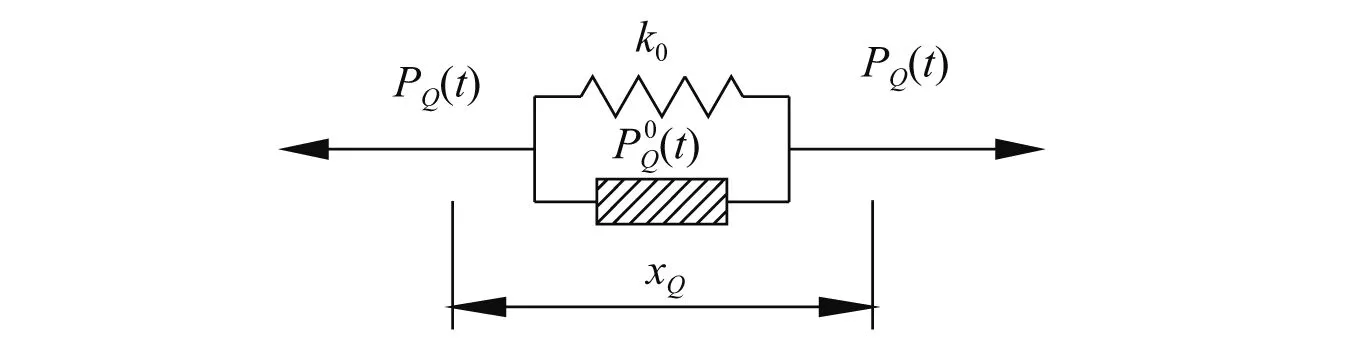
图1 一般积分型阻尼器模型Fig.1 General integral damper model

一般积分型阻尼器模型的本构方程[19-23]可表示为

(1)

(2)

hQ(t)=Q(t)-Q(+∞)

(3)

式中：PQ(t)为一般积分型阻尼器的受力；xQ(t)为阻尼器的相对位移；Q(t)，k0和hQ(t)分别为阻尼器的松弛模量函数、平衡刚度和松弛函数。

1.2 设置支撑的一般黏弹性阻尼器等效模型

工程上，阻尼器往往与支撑串联安装在结构中，以发挥减震效果。现将水平支撑与阻尼器的整体串联系统作为等效阻尼器PG(t)以考虑水平支撑刚度kb对阻尼器响应特性的影响，其计算模型如图2所示。设kG，hG(t)和G(t)分别为等效阻尼器PG(t)的平衡刚度、松弛函数和松弛模量函数，等效阻尼器PG(t)的计算模型如图3所示。

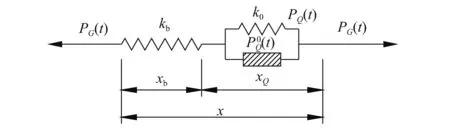
图2 设置支撑一般线性黏弹性阻尼器计算模型Fig.2 The calculation model of general linear viscoelastic damper with support

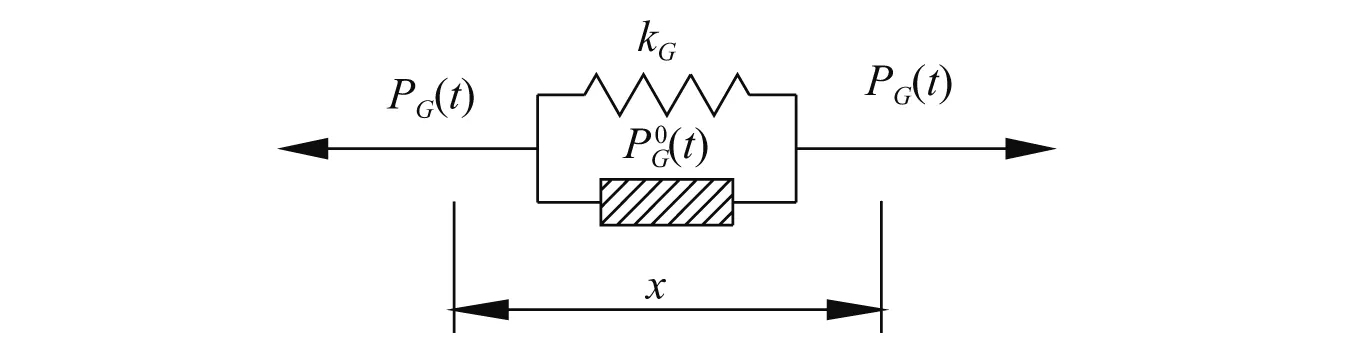
图3 等效阻尼器计算模型Fig.3 The calculation model of equivalent damper

设置支撑一般黏弹性阻尼器等效模型[24]的本构方程可表示为

(4)

(5)

设xb为水平支撑kb的相对位移，xQ为阻尼器PQ(t)的相对位移，x为等效阻尼器PG(t)的相对位移，则阻尼器PQ(t)的力和变形满足

x=xQ+xb

(6)

PQ(t)=kbxb=PG(t)

(7)

式中

(8)

(9)

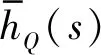
1.3 Maxwell阻尼器模型

Maxwell阻尼器模型具有本构方程[25]简便，试验拟合精度高，计算方便，易于扩阶分析等优点被广泛关注。该模型可表示为耗能单元与弹簧单元串联，其计算模型如图4所示。

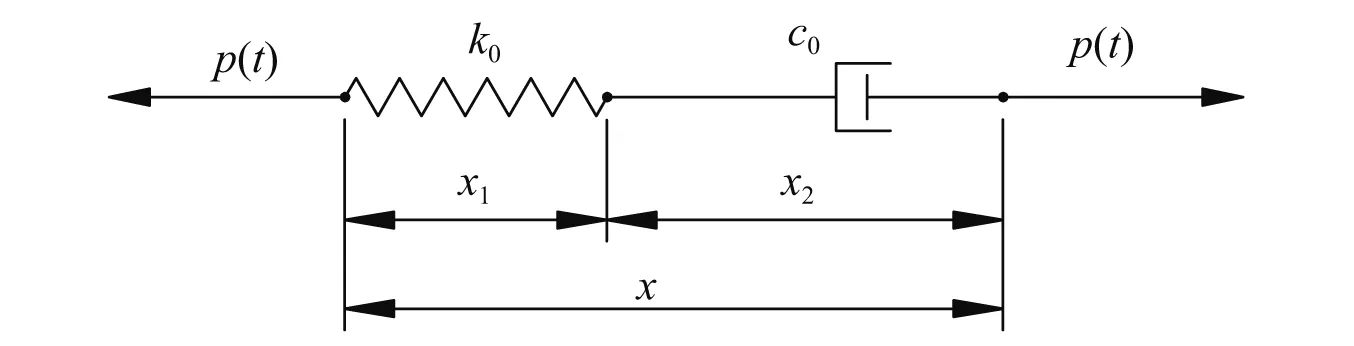
图4 Maxwell阻尼器模型Fig.4 Maxwell damper model

Maxwell阻尼器模型的本构方程可表示为

(10)

式中：x(t)为阻尼器相对位移；c0为阻尼系数；k0为刚度系数。

x(t)=x1(t)+x2(t)

(11)

(12)

1.4 结构运动方程的建立

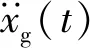
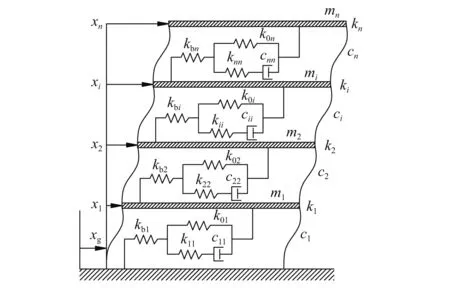
图5 结构计算模型Fig.5 Structural calculation model

(13)

(14)

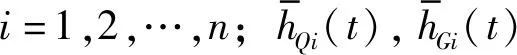
由前期研究可得

(15)

(16)

(17)

(18)

式中,

KG=Ldiag[kGi]LT，(i=1,2,…,n)

(19)

μii=kii/cii，(i=1,2,…,n)

(20)

(21)

1=[1 1 … 1]T

(22)

(23)

将式(14)代入式(13)，结构运动方程可化为

(24)

对式(16)取拉氏逆变换可得

hGi(t)=kaie-μait

(25)

(26)

1.5 扩阶方程的建立

令

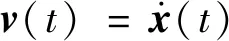
(27)

式(13)、式(27)和式(14)以扩阶的形式表示为

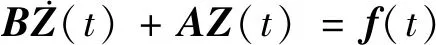
(28)

式中,

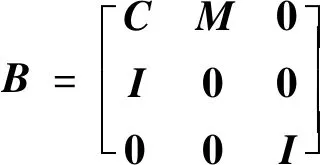
(29)

(30)

(31)

(32)

2 非均匀和完全非平稳响应分析的虚拟激励法

2.1 非平稳地震激励模型

(33)

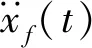
(34)

2.2 非均匀和完全非平稳响应的虚拟激励法

(35)

式(28)可改写为

(36)

对于一般黏弹性阻尼耗能结构系统，其运动方程可以按照文献[26-28]提出的扩阶方法化为式(36)的形式，所以本文方法不仅适用于Maxwell阻尼耗能结构系统，也适用于一般黏弹性阻尼耗能结构系统。

其中，

(37)

式(36)的通解为齐次解与特解之和，即

Z(ω,t)=T(τ)(Z(ω,tk)-Zp(ω,tk))+Zp(ω,t)

(38)

式中：t为积分步长，t∈[tk,tk+1]；τ=t-tk；关于指数矩阵T(τ)的精细计算，详见林家浩等的研究。问题归结为求特解Zp(ω,t)及精细地计算T(τ)。

3 虚拟激励下响应的一般精细积分格式

由式(34)和式(37)，激励荷载在每一积分步长t∈[tk,tk+1]内可表示为

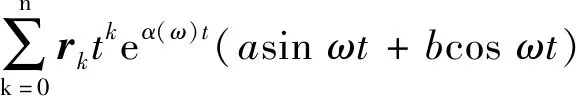
(39)

式中：

rk=-B-1f1(ω)εk(ω),(k=0～n);a=i;b=1

(40)

将式(39)代入式(36)，可得方程特解Zp(ω,t)为

(41)

式中,

an=((α(ω)I-H)2+ω2I)-1((α(ω)I-H)arn+ωbrn),bn=((α(ω)I-H)2+ω2I)-1((α(ω)I-H)brn-ωarn),aj=((α(ω)I-H)2+ω2I)-1×((α(ω)I-H)×(arj-(j+1)aj+1)+ω(brj-(j+1)bj+1)),bj=((α(ω)I-H)2+ω2I)-1×((α(ω)I-H)×(brj-(j+1)bj+1)-ω(arj-(j+1)aj+1)),(j=n-1,n-2,…,0)

(42)

由式(38)和式(41)均匀与非均匀非平稳、完全非平稳响应的简谐-指数-多项式精细积分一般通用精确格式可表示为

Z(ω,tk+1)=T(τ)(Z(ω,tk)-Zp(ω,tk))+Zp(ω,tk+1)

(43)

式(39)可以退化为林家浩等提出的简谐、多项式简谐、指数衰减型简谐三种精细积分格式，由于篇幅有限仅简单介绍：当激励荷载中rk=0，(k=1～n)，α=0时，可退化为简谐荷载精细积分格式；当激励荷载中rk=0，(k=3～n)，α=0时，可退化为多项式简谐荷载精细积分格式；当激励荷载中rk=0，(k=1～n)时，可退化为指数衰减型简谐荷载精细积分格式。

由式(31)和式(43),可以得到的响应为z(ω,t)，那么该响应的自谱密度及方差可表示为

Szz(ω,t)=z*(ω,t)z(ω,t)

(44)

(45)

式中，“*”为复共轭。

综上步骤，设置支撑的Maxwell阻尼耗能系统的均匀与非均匀非平稳、完全非平稳响应方差均可得到。

4 8种经典调制非平稳响应的解析解

由式(43)可得，精细积分精确格式可由特解求出，为节省篇幅以下计算只给出特解。

4.1 Shinozuka-Sato型调制函数

g(t)=e-λ1t-e-λ2t

(46)

式中，λ1，λ2为已知常数。

f0(ω,t)=(r0,0eα0,0(ω)t+r0,1eα0,1(ω)t)×
(asinωt+bcosωt)

(47)

式中：

r0,0=-B-1f1ε0,0;ε0,0=1;α0,0=-λ1;r0,1=-B-1f1ε0,1;ε0,1=-1;α0,1=-λ2;a=i;b=1

(48)

特解可求得

Zp(ω,t)=(a0,0eα0,0t+a0,1eα0,1t)sinωt+
(b0,0eα0,0t+b0,1eα0,1t)cosωt

(49)

式中,

a0,1=((α0,1I-H)2+ω2I)-1×
((α0,1I-H)ar0,1+ωbr0,1),b0,1=((α0,1I-H)2+ω2I)-1×
((α0,1I-H)br0,1-ωar0,1),a0,0=((α0,0I-H)2+ω2I)-1×
((α0,0I-H)ar0,0+ωbr0,0),b0,0=((α0,0I-H)2+ω2I)-1×
((α0,0I-H)br0,0-ωar0,0)

(50)

4.2 Hsu-Bernard型调制函数

g(t)=εte-λt

(51)

式中：ε=λe；λ为已知常数。

f0(ω,t)=r1teα1t(asinωt+bcosωt)

(52)

式中：

r1=-B-1f1ε1;ε1=λe;α1=-λ;a=i;b=1

(53)

特解可求得

Zp(ω,t)=(a0+a1t)eα1tsinωt+
(b0+b1t)eα1tcosωt

(54)

式中,

a1=((α1I-H)2+ω2I)-1((α1I-H)ar1+ωbr1),b1=((α1I-H)2+ω2I)-1((α1I-H)br1-ωar1),a0=((α1I-H)2+ω2I)-1×
((α1I-H)(-a1)+ω(-b1)),b0=((α1I-H)2+ω2I)-1×
((α1I-H)(-b1)-ω(-a1))

(55)

4.3 Goto-Toki型调制函数

(56)

式中，A0，tp为已知常数。

f0(ω,t)=r1teα1t(asinωt+bcosωt)

(57)

式中：

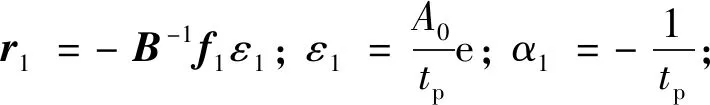
(58)

特解可求得

Zp(ω,t)=(a0+a1t)eα1tsinωt+
(b0+b1t)eα1tcosωt

(59)

式中,

a1=((α1I-H)2+ω2I)-1((α1I-H)ar1+ωbr1),b1=((α1I-H)2+ω2I)-1((α1I-H)br1-ωar1),a0=((α1I-H)2+ω2I)-1×
((α1I-H)(-a1)+ω(-b1)),b0=((α1I-H)2+ω2I)-1×
((α1I-H)(-b1)-ω(-a1))

(60)

4.4 Iyengar型调制函数

g(t)=(c+dt)e-λt

(61)

式中，c，d，λ为已知常数。

f0(ω,t)=(r0eα0t+r1teα1t)(asinωt+bcosωt)

(62)

式中：

r0=-B-1f1ε0;ε0=c;α0=-λ;r1=-B-1f1ε1;ε1=d;α1=-λ;a=i;b=1

(63)

特解可求得

Zp(ω,t)=(a0eα0t+a1teα1t)sinωt+
(b0eα0t+b1teα1t)cosωt

(64)

式中，

a1=((α1I-H)2+ω2I)-1((α1I-H)ar1+ωbr1),b1=((α1I-H)2+ω2I)-1((α1I-H)br1-ωar1),a0=((α0I-H)2+ω2I)-1×
((α0I-H)(ar0-a1)+ω(br0-b1)),b0=((α0I-H)2+ω2I)-1×
((α0I-H)(br0-b1)-ω(ar0-a1))

(65)

4.5 分段型调制函数

(66)

式中，A0，c，t1，t2为已知常数。

当0≤t≤t1时

f0(ω,t)=r2t2eα2t(asinωt+bcosωt)

(67)

式中：

(68)

特解可求得

Zp(ω,t)=(a0+a1t+a2t2)sinωt+
(b0+b1t+b2t2)cosωt

(69)

式中,

a2=((α2I-H)2+ω2I)-1((α2I-H)ar2+ωbr2),b2=((α2I-H)2+ω2I)-1((α2I-H)br2-ωar2),a1=((α2I-H)2+ω2I)-1×
((α2I-H)(-2a2)+ω(-2b2)),b1=((α2I-H)2+ω2I)-1×
((α2I-H)(-2b2)-ω(-2a2)),a0=((α2I-H)2+ω2I)-1×
((α2I-H)(-a1)+ω(-b1)),b0=((α2I-H)2+ω2I)-1×
((α2I-H)(-b1)-ω(-a1))

(70)

当t1≤t≤t2时，

f0(ω,t)=r0eα0t(asinωt+bcosωt)

(71)

式中：

r0=-B-1f1ε0;ε0=A0;α0=0;a=i;b=1

(72)

特解可求得

Zp(ω,t)=a0sinωt+b0cosωt

(73)

式中，

a0=(H2+ω2I)-1(-Har0+ωbr0),b0=(H2+ω2I)-1(-Hbr0-ωar0)

(74)

当t≥t2时，

f0(ω,t)=(r0eα0t+r1teα1t)(asinωt+bcosωt)

(75)

式中：

r0=-B-1f1ε0;ε0=-A0e-ct2;α0=0;r1=-B-1f1ε1;ε1=A0e-c;α0=0;a=i;b=1

(76)

特解可求得

Zp(ω,t)=(a0+a1t)sinωt+(b0+b1t)cosωt

(77)

式中，

a1=(H2+ω2I)-1(-Har1+ωbr1),b1=(H2+ω2I)-1((-Hbr1)-ωar1),a0=(H2+ω2I)-1((-H(ar0-a1))+ω(br0-b1)),b0=(H2+ω2I)-1×
((-H(br0-b1))-ω(ar0-a1))

(78)

4.6 余弦型调制函数

g(t)=c+dcosθt

(79)

式中，c，d，θ为已知常数，c≥d。

f0(ω,t)=(r0,0eα0,0t+r0,1eα0,1t+r0,2eα0,2t)×
(asinωt+bcosωt)

(80)

式中：

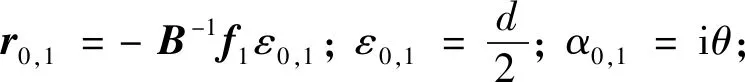
(81)

特解可求得

Zp(ω,t)=(a0,0+a0,1eα0,1t+a0,2eα0,2t)sinωt+
(b0,0+b0,1eα0,1t+b0,2eα0,2t)cosωt

(82)

式中,

a0,2=((α0,2I-H)2+ω2I)-1×
((α0,2I-H)ar0,2+ωbr0,2),b0,2=((α0,2I-H)2+ω2I)-1×
((α0,2I-H)br0,2-ωar0,2),a0,1=((α0,1I-H)2+ω2I)-1×
((α0,1I-H)ar0,1+ωbr0,1),b0,1=((α0,1I-H)2+ω2I)-1×
((α0,1I-H)br0,1-ωar0,1),a0,0=(H2+ω2I)-1((-Har0,0)+ωbr0,0),

b0,0=(H2+ω2I)-1((-Hbr0,0)-ωar0,0)

(83)

4.7 正弦型调制函数

g(t)=c+dsinθt

(84)

式中，c，d，θ为已知常数，c≥d。

f0(ω,t)=(r0,0eα0,0t+r0,1eα0,1t+r0,2eα0,2t)×
(asinωt+bcosωt)

(85)

式中：

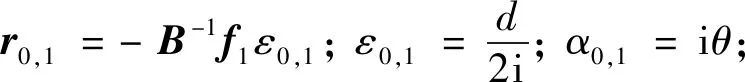
(86)

特解可求得

Zp(ω,t)=(a0,0+a0,1eα0,1t+a0,2eα0,2t)sinωt+
(b0,0+b0,1eα0,1t+b0,2eα0,2t)cosωt

(87)

式中,

a0,2=((α0,2I-H)2+ω2I)-1×
((α0,2I-H)ar0,2+ωbr0,2),b0,2=((α0,2I-H)2+ω2I)-1×
(α0,2I-H)br0,2-ωar0,2),a0,1=((α0,1I-H)2+ω2I)-1×
((α0,1I-H)ar0,1+ωbr0,1),b0,1=((α0,1I-H)2+ω2I)-1×
((α0,1I-H)br0,1-ωar0,1),a0,0=(H2+ω2I)-1((-Har0,0)+ωbr0,0),b0,0=(H2+ω2I)-1((-Hbr0,0)-ωar0,0)

(88)

4.8 Spanos-Solomos型非均匀调制函数

g(ω,t)=ε(ω)te-λ(ω)t

(89)

式中，ε(ω)，λ(ω)为以ω为自变量的函数。

f0(ω,t)=r1teα1t(asinωt+bcosωt)

(90)

式中：

r1=-B-1f1ε1;ε1=ε(ω);α1=-λ(ω);a=i;b=1

(91)

特解可求得

Zp(ω,t)=(a0+a1t)eα1tsinωt+
(b0+b1t)eα1tcosωt

(92)

式中,

a1=((α1I-H)2+ω2I)-1((α1I-H)ar1+ωbr1),b1=((α1I-H)2+ω2I)-1((α1I-H)br1-ωar1),a0=((α1I-H)2+ω2I)-1×
((α1I-H)(-a1)+ω(-b1)),b0=((α1I-H)2+ω2I)-1×
((α1I-H)(-b1)-ω(-a1))

(93)

5 Conte-Peng非平稳功率谱模型

Conte和Peng提出的由实际的地震加速度演变功率谱经自适应最小二乘法拟合得到的完全非平稳功率谱模型

(94)

gf(t)=εf(t-tf)rfe-αf(t-tf)U(t-tf)

(95)

式中：f=1，…，Nf；U(t-tf)为单位阶跃函数。

(96)

(97)

f0(ω,t)=rrf(t-tf)rfeαf(t-tf)(asinωt+bcosωt)

(98)

式中：

rrf=-B-1f1(ω)εf;a=i;b=1

(99)

特解可求得

(100)

式中,

arf=((αfI-H)2+ω2I)-1((αfI-H)arrf+ωbrrf),brf=((αfI-H)2+ω2I)-1((αfI-H)brrf-ωarrf),aj=((αfI-H)2+ω2I)-1×((αfI-H)×
(-(j+1)aj+1)+ω(-(j+1)bj+1)),bj=((αfI-H)2+ω2I)-1×((αfI-H)×
(-(j+1)bj+1)-ω(-(j+1)aj+1)),(j=rf-1,rf-2,…,0)

(101)

6 算 例

6.1 单自由度算例

单自由度设置支撑的Maxwell阻尼器减震系统，如图6所示。其结构的基本参数为：质量m=42 500 kg；刚度k=145.43×105N/m；阻尼比s0分别取0.02，0.04，0.08，0.20。Maxwell阻尼器的基本参数为：平衡刚度为k0=0.36×105N/m；支撑刚度为kb=1.5k；Maxwell阻尼器刚度和阻尼分别为k1=42.08×105N/m，c1=0.83×105N·s/m。

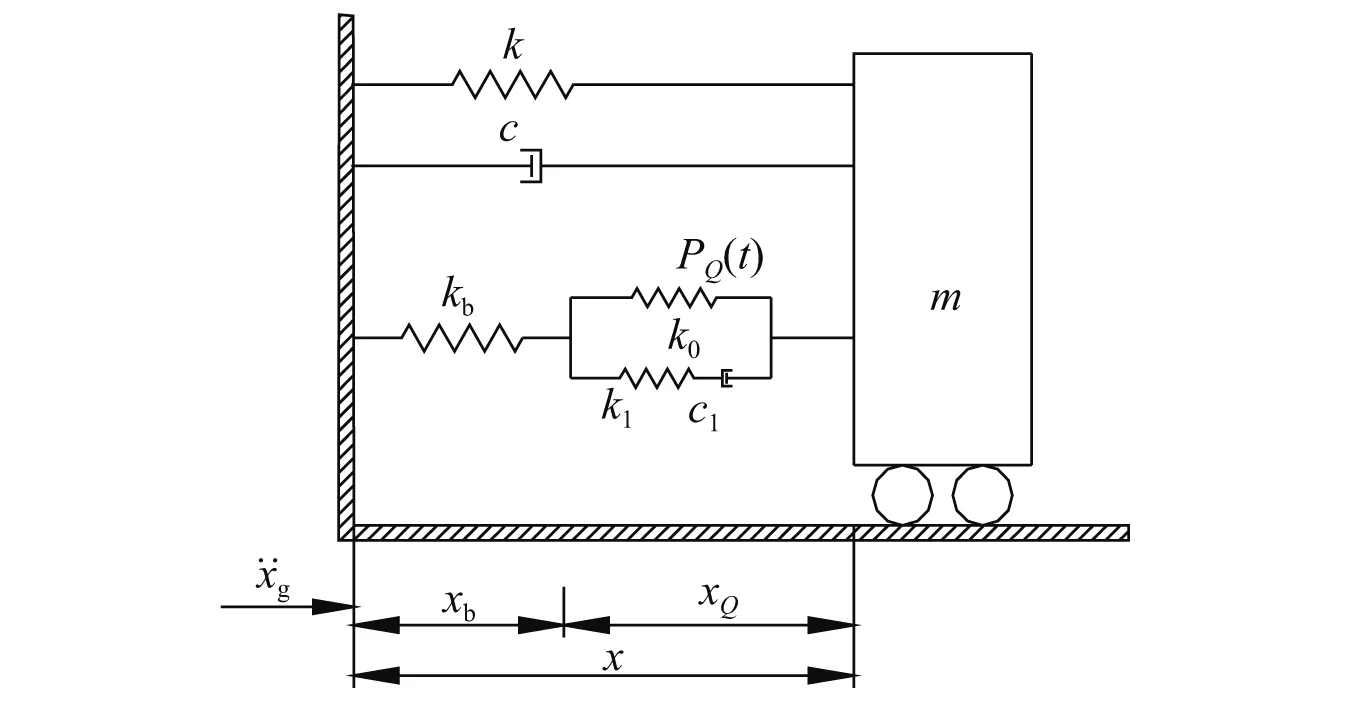
图6 结构计算模型Fig.6 Structural calculation model

式中：ωf取19 rad/s；ξf取0.65；S0取0.015 54 m2/s3。

调幅函数分别取为Shinozuka-Sato型[29]均匀调幅和Spanos-Solomos型[30]非均匀调幅，计算参数分别取为

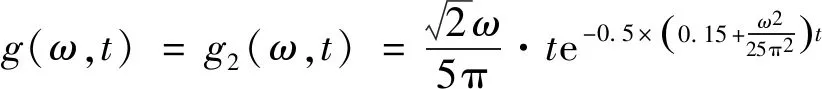
首先运用本文方法得到Shinozuka-Sato型非平稳地震作用下的响应方差，如图7～图12所示。最后进一步应用到Spanos-Solomos型非均匀调制非平稳地震激励作用下结构响应方差，如图13～图18所示。可以看出：在均匀与非均匀非平稳激励下，耗能系统的响应具有相似波动趋势的特点，表现出明显的非平稳随机特性，符合工程实际。

为了研究阻尼比对结构响应的影响，s0分别取0.02，0.04，0.08，0.20。阻尼比取值的不同对耗能系统的响应有较大的影响，在两类非平稳地震作用下，耗能系统的响应，如图7～图9和图13～图15所示。随着阻尼比的增大，结构的整体响应强度越小，阻尼比越大，结构达到静止的时间越早，相应的峰值也会提前，即随着阻尼比的增大，响应也随之越早达到峰值，但响应方差反而减小。

图7 Shinozuka-Sato调幅函数下结构位移响应方差Fig.7 Structural displacement response variance under Shinozuka-Sato amplitude modulation function

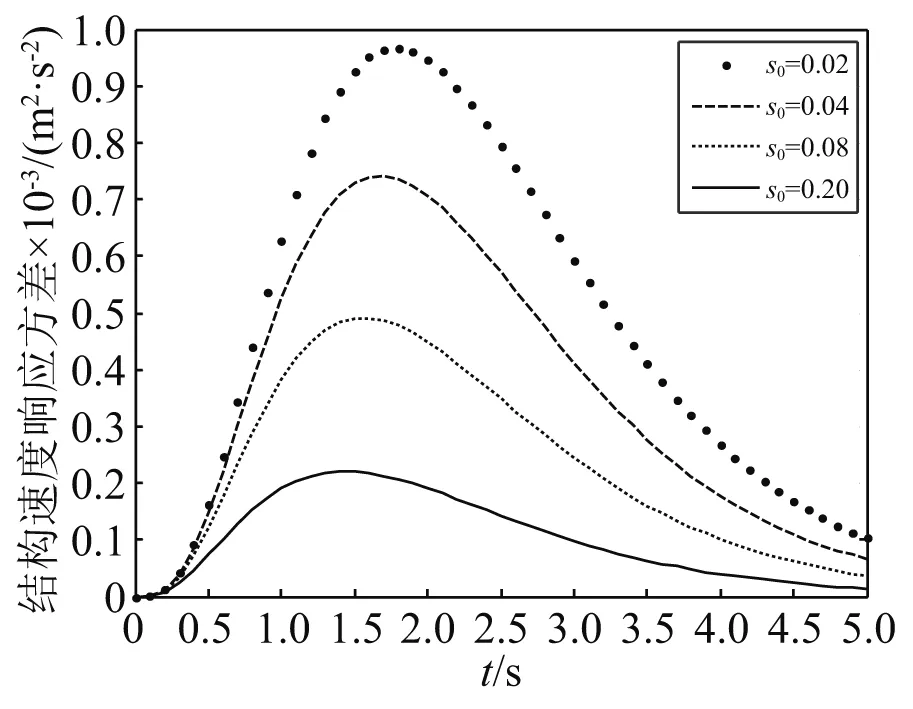
图8 Shinozuka-Sato调幅函数下结构速度响应方差Fig.8 Structural velocity response variance under Shinozuka-Sato amplitude modulation function

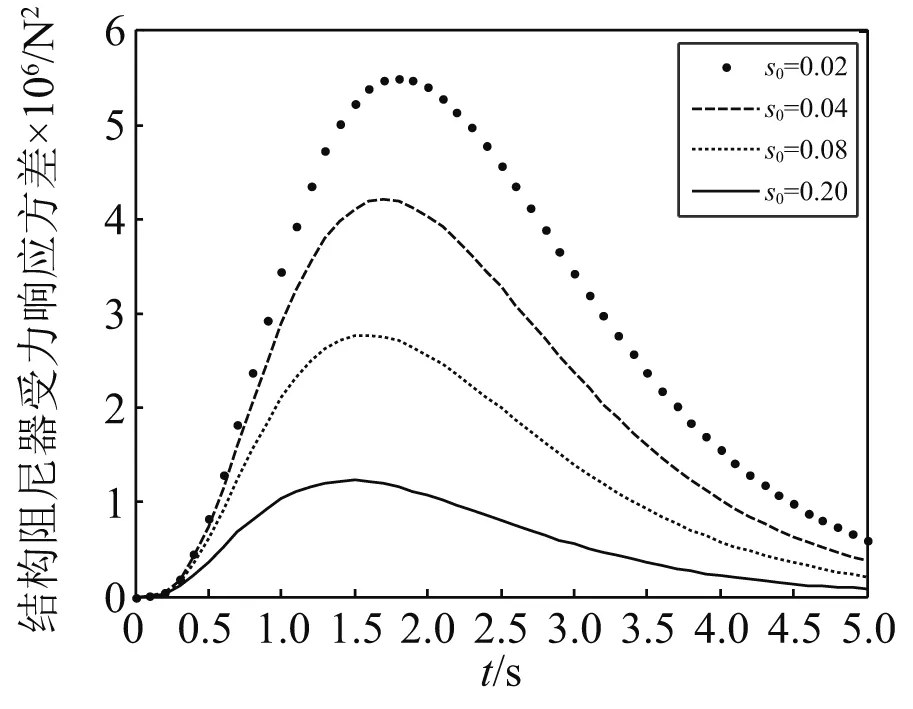
图9 Shinozuka-Sato调幅函数下阻尼器受力响应方差Fig.9 Variance of damper response under Shinozuka-Sato amplitude modulation function

为了研究支撑刚度对结构响应的影响，结构基本参数不变，而rb分别为0.5，0.8，1.2，10.0，∞，支撑刚度kb=rbk，rb为支撑刚度除结构刚度，阻尼比取s0=0.1，在两类非平稳地震作用下，耗能系统的响应，如图10～图12和图16～图18所示。支撑刚度取值的不同对耗能系统的响应有较大的影响，然而对产生响应最大值的时刻影响较小，随着支撑刚度取值的增大，阻尼器受力响应方差也随之增大，但是结构的位移、速度响应方差反而减小。

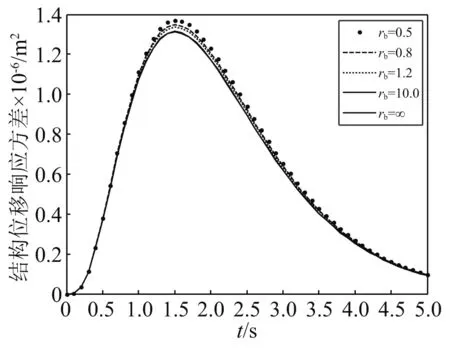
图10 Shinozuka-Sato调幅函数下结构位移响应方差Fig.10 Structural displacement response variance under Shinozuka-Sato amplitude modulation function

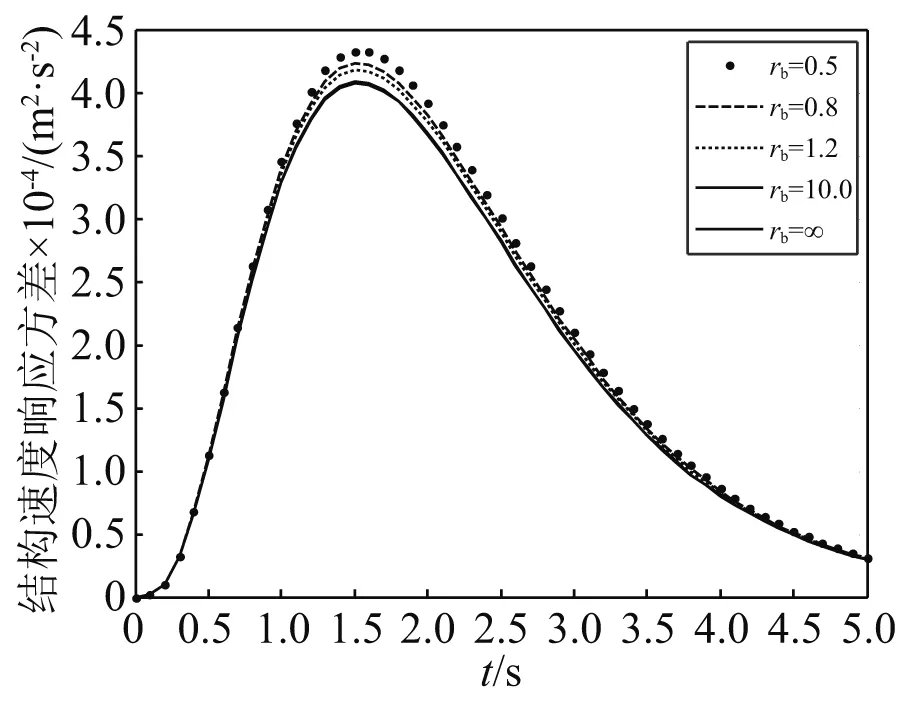
图11 Shinozuka-Sato调幅函数下结构速度响应方差Fig.11 Structural velocity response variance under Shinozuka-Sato amplitude modulation function

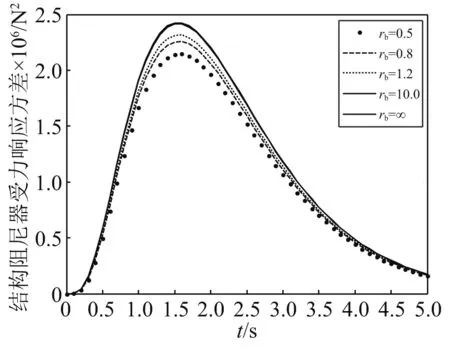
图12 Shinozuka-Sato调幅函数下阻尼器受力响应方差Fig.12 Variance of damper response under Shinozuka-Sato amplitude modulation function

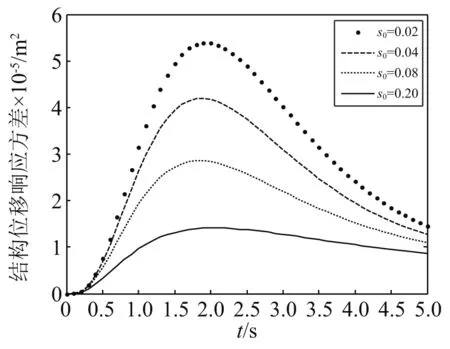
图13 Spanos-Solomos调幅函数下结构位移响应方差Fig.13 Structural displacement response variance under Spanos-Solomos amplitude modulation function

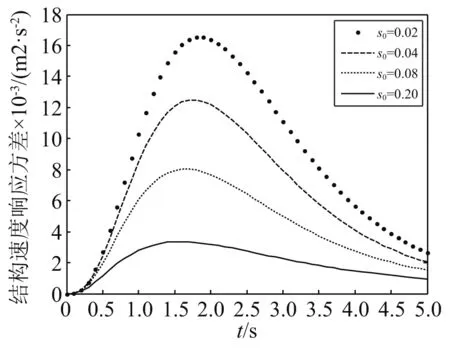
图14 Spanos-Solomos调幅函数下结构速度响应方差Fig.14 Structural velocity response variance under Spanos-Solomos amplitude modulation function

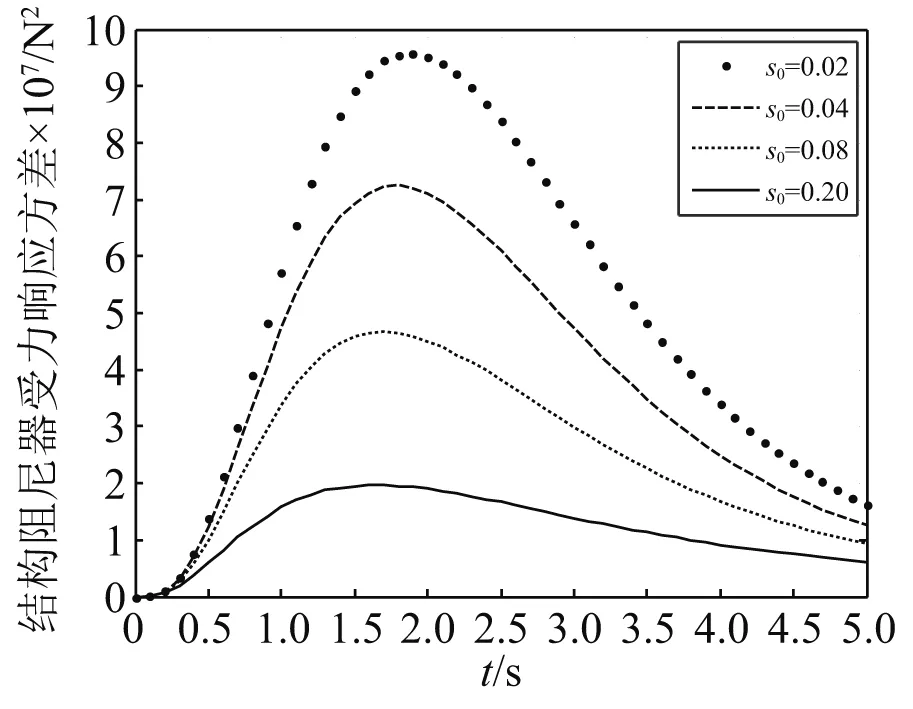
图15 Spanos-Solomos调幅函数下阻尼器受力响应方差Fig.15 Variance of damper response under Spanos-Solomos amplitude modulation function

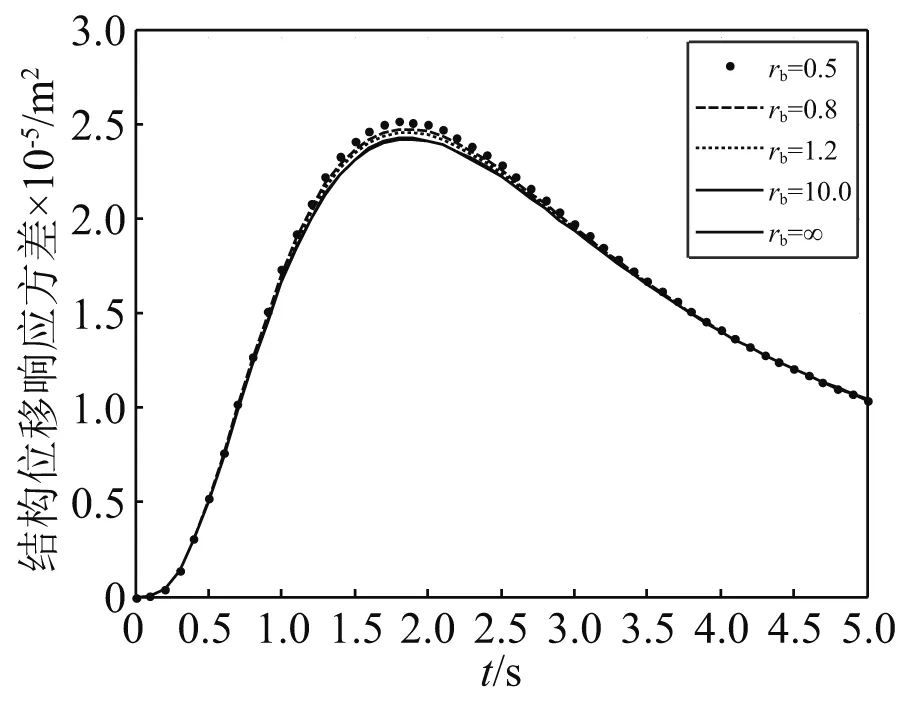
图16 Spanos-Solomos调幅函数下结构位移响应方差Fig.16 Structural displacement response variance under Spanos-Solomos amplitude modulation function

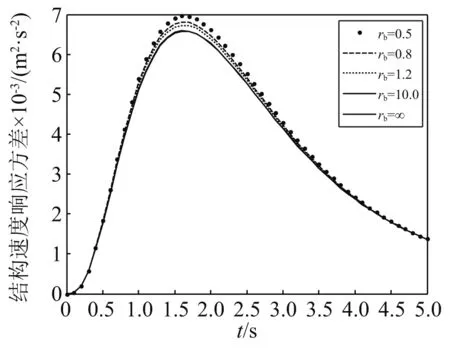
图17 Spanos-Solomos调幅函数下结构速度响应方差Fig.17 Structural velocity response variance under Spanos-Solomos amplitude modulation function

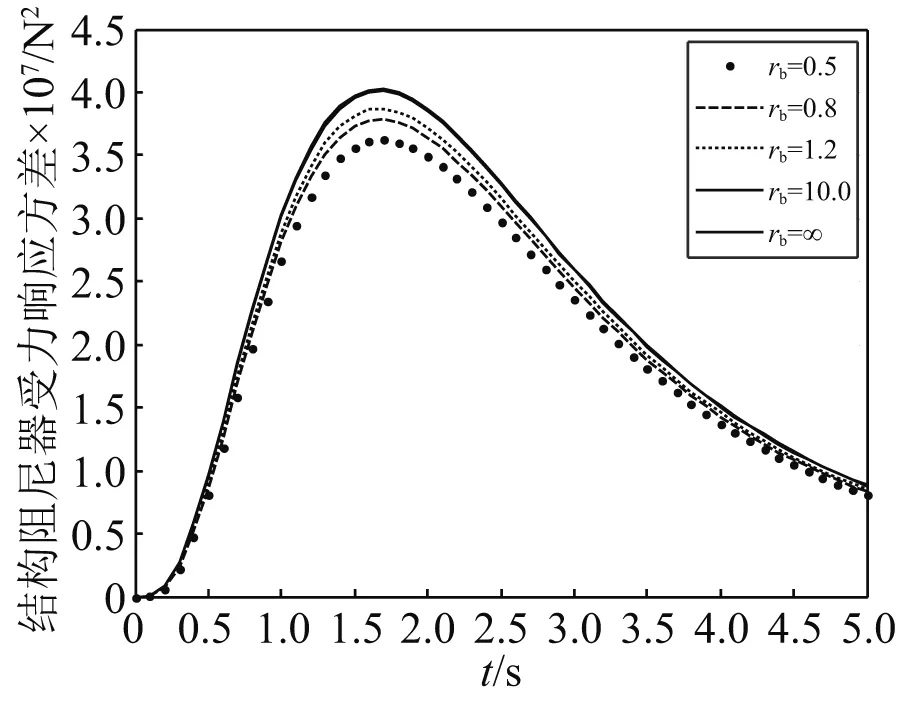
图18 Spanos-Solomos调幅函数下阻尼器受力响应方差Fig.18 Variance of damper response under Spanos-Solomos amplitude modulation function

为保证结构获得很好的耗能作用，在支撑刚度kb≥10k情况下，可以按kb=∞近似计算；在kb较小情况下，可以按kb的实际刚度进行计算。

6.2 多自由度算例

某3层设置支撑的Maxwell阻尼器减震系统，如图19所示。其结构的基本参数为：质量m1=3.86×104kg，m2=3.68×104kg，m3=3.59×104kg；刚度k1=146.01×105N/m，k2=133.25×105N/m，k3=101.91×105N/m；阻尼比ξ0=0.05。每一层采用相同的Maxwell阻尼器：平衡刚度度k0=0.36×105N/m，k1=42.08×105N/m，c1=0.83×105N·s/m;支撑刚度为kb=3k1。

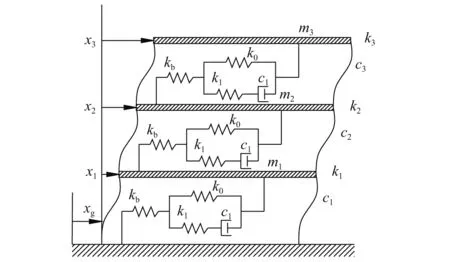
图19 结构计算模型Fig.19 Structural calculation model

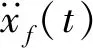
式中：ωf取19 rad/s；ξf取0.65；S0取0.015 54 m2/s3。

调幅函数分别取为Shinozuka-Sato型均匀调幅和Spanos-Solomos型非均匀调幅，计算参数分别取为

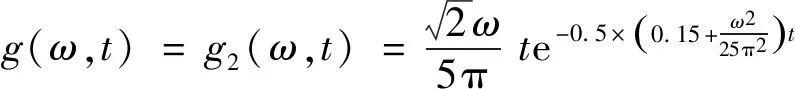
在Shinozuka-Sato型均匀调幅非平稳地震激励作用下，多层减震结构系统的位移、速度、阻尼器受力响应方差，如图20～图22所示。

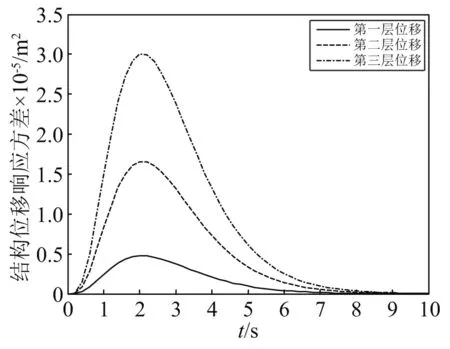
图20 Shinozuka-Sato调幅函数下结构位移响应方差Fig.20 Structural displacement response variance under Shinozuka-Sato amplitude modulation function

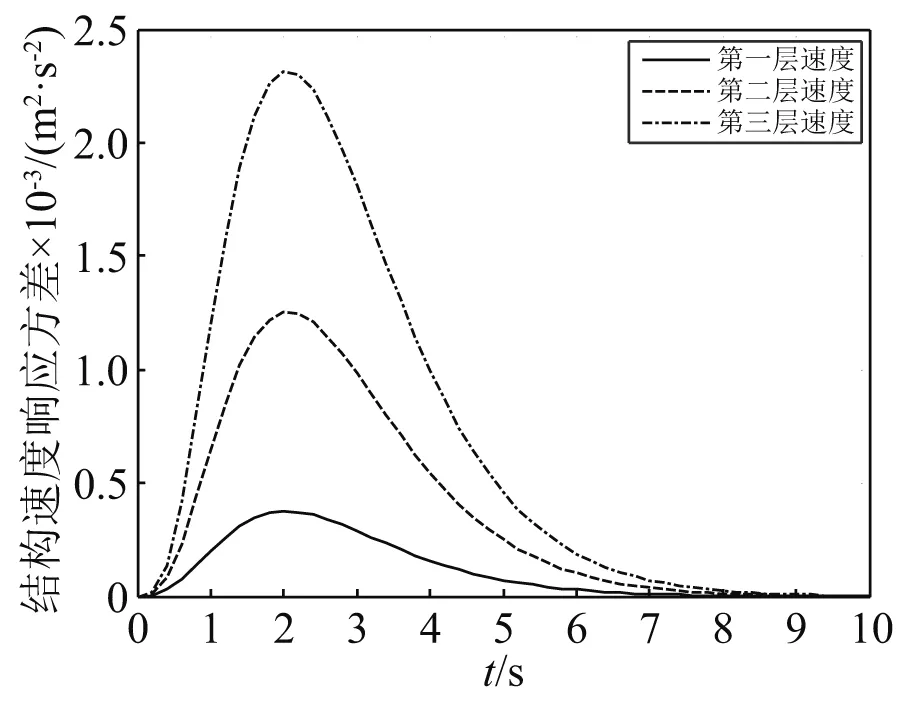
图21 Shinozuka-Sato调幅函数下结构速度响应方差Fig.21 Structural velocity response variance under Shinozuka-Sato amplitude modulation function

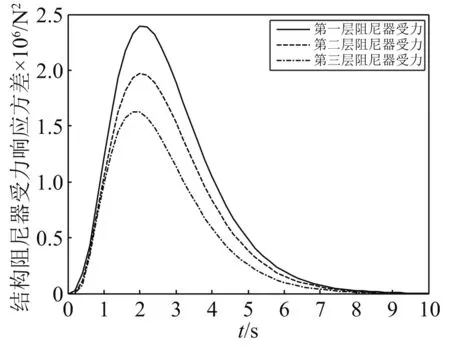
图22 Shinozuka-Sato调幅函数下阻尼器受力响应方差Fig.22 Variance of damper response under Shinozuka-Sato amplitude modulation function

在Spanos-Solomos型非均匀调幅非平稳地震激励作用下，多层减震结构系统的位移、速度、阻尼器受力响应方差，如图23～图25所示。

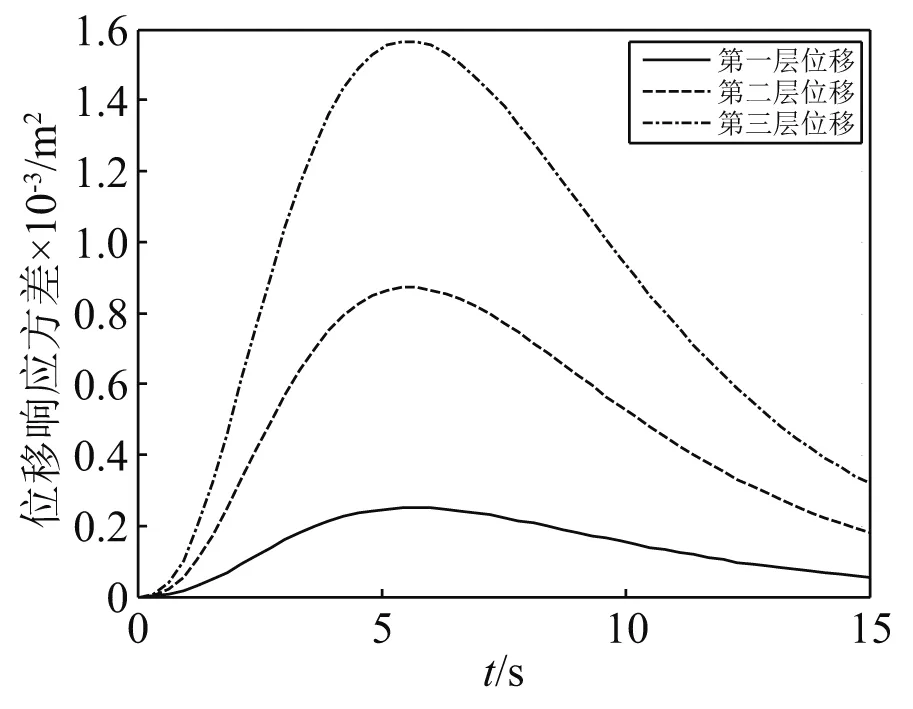
图23 Spanos-Solomos调幅函数下结构位移响应方差Fig.23 Structural displacement response variance under Spanos-Solomos amplitude modulation function

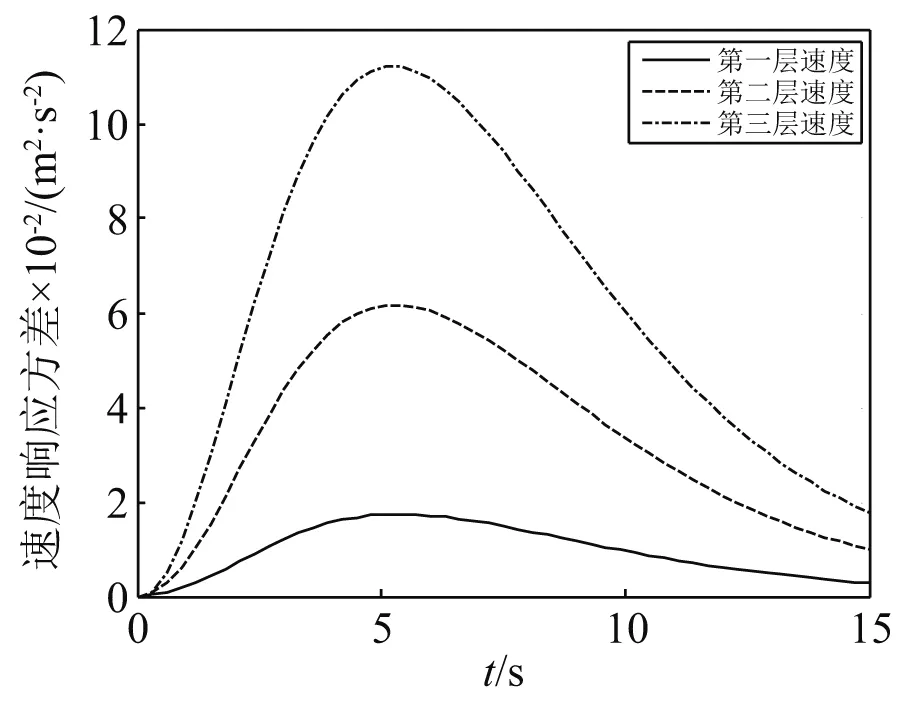
图24 Spanos-Solomos调幅函数下结构速度响应方差Fig.24 Structural velocity response variance under Spanos-Solomos amplitude modulation function

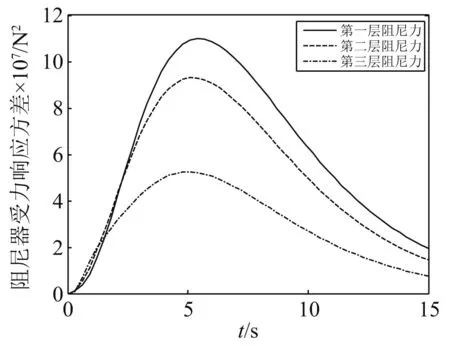
图25 Spanos-Solomos调幅函数下阻尼器受力响应方差Fig.25 Variance of damper response under Spanos-Solomos amplitude modulation function

由计算结果可以看出：在多自由度系统下，各层响应方差均随其调制函数的变化而变化，图形与调制函数图形基本一致。

7 结 论

为建立黏弹性耗能结构及其保护系统的抗震分析与设计方法，本文将虚拟激励法引入黏弹性耗能阻尼系统，获得了均匀与非均匀非平稳、完全非平稳响应的简谐-指数-多项式精细积分一般通用精确格式，得到了8种经典均匀与非均匀调制非平稳、完全非平稳地震响应的具体解析解，使计算结果不受步长影响；最后，可得出耗能结构系统的均匀与非均匀非平稳、完全非平稳地震响应方差。

(1)通过算例，验证了本文方法的正确性与可行性，该方法适应于设置支撑的Maxwell阻尼系统的均匀与非均匀非平稳、完全非平稳响应分析，并且可直接应用于黏弹性阻尼耗能系统响应分析。支撑刚度对黏弹性耗能系统有重要影响，在支撑刚度较耗能系统刚度很大情况下，支撑刚度对耗能系统响应的影响效果不再增加，一般情况下，应考虑有限支撑刚度对耗能系统响应的影响。

(2)本文均匀与非均匀非平稳、完全非平稳响应的精细积分一般精确格式，不受计算步长的影响，任意步长计算效果都是精确的。简谐、多项式简谐、指数简谐型精细积分格式都可以用本文精细积分一般精确格式表示，应用范围更加广泛。本文得到8种经典均匀与非均匀调制非平稳以及完全非平稳随机地震响应分析的精细积分精确格式，使用方便、效率高、工程应用强。