基于时变模态振型小波变换的结构损伤识别方法

王 盟，翁 顺，余兴胜，闫俊锋，殷鹏程

(1.华中科技大学 土木工程与力学学院，武汉 430074；2.华中科技大学 控制结构湖北省重点实验室，武汉 430074；3.中铁第四勘察设计院集团有限公司，武汉 430063)

结构模态参数是大型土木工程结构优化设计、振动控制和损伤识别等研究领域的重要参数之一[1]。由于材料非线性、几何非线性和状态非线性等原因，土木工程结构本身是非线性的，其模态参数是时变的。结构损伤是一种非线性发展过程，也体现为时变的模态参数。结构损伤将导致结构模态参数的变化，如频率、阻尼和振型。结构的振型包含了结构各个节点的信息，因此可以通过时变模态振型特征识别结构损伤位置和损伤程度。大多数传统的模态参数识别方法都是基于时域或者频域[2]，如快速傅里叶变换(fast Fourier transform，FFT)、时序分析法以及分区模态综合法等。这些传统方法虽然能识别出结构的模态参数[3]，但是也存在很多缺点：①频域方法和时域方法都只能在频域空间或时域空间中进行，而不能获得信号在频域空间和时域空间内的联系，在实际应用中存在某些限制，例如，傅里叶变换只能得到信号中包含的频率，但是却不能得到这些频率所对应的时域特征；②传统方法大多数只适用于线性结构，然而实际上土木工程结构是非线性的，它的模态参数是时变的，传统的识别方法难以展示时变特性。

目前时变模态参数识别方法主要有短时傅里叶变换(short time Fourier transform,STFT)、Hilbert-Huang变换(Hilbert-Huang transform,HHT)、Cohen类时频分布、小波变换等[4]。STFT是使用一个固定的窗函数对信号进行傅里叶变换分析，通过移动窗函数来逐步分析信号，从而得到信号的时变特性[5]。刘小峰等[6]通过STFT方法，成功地对旋转机械信号进行了精细时频分析。STFT方法缺点在于其窗函数是固定的，因此它的分辨率是固定的，要改变分辨率必须更改窗函数。HHT方法主要包括经验模态分解和Hilbert变换，这种方法的自适应性很强[7]。胡浩然等[8]结合奇异谱分析技术和HHT方法，准确地识别了故宫木结构古建筑的时变模态参数。HHT方法目前最大的问题是缺乏严谨完整的理论基础。Cohen类时频分布主要包括伪Wigner-Ville分布、平滑伪Wigner-Ville分布、Choi-Willams分布等[9]。郭奇等[10]结合二次聚合经验模态分解和Wigner-Ville分布方法，改善了模态混叠问题。Cohen类时频分布方法的缺点在于无法完全消除交叉项影响，从而造成虚假频率成分产生。小波变换是一种窗口大小固定但形状可变，时域和频域分辨率都可改变的时频局部化分析方法。它既克服了STFT分辨率固定的缺点，又能准确分析信号的真实频率成分，并且有严谨完整的理论基础，已经成为分析时变结构模态参数的重要方法[11]。

利用小波变换的多分辨率特性和时频特性，可以得到瞬时频率以及瞬时振型。Lardies[12]通过对结构信号进行连续小波变换，成功识别了线性时不变结构的频率和振型。滕军等[13]将复Morlet小波变换方法应用于大跨度空间结构，成功识别出了大跨度空间结构的频率和振型。王超等[14]提出了一种基于动态规划提取多成分信号小波脊和瞬时频率的方法，通过找到小波系数模极大值，提取小波脊线，从而识别出时变结构的瞬时频率。

将结构损伤当作一种非线性，它将引起结构模态振型的时变特征，因此通过时变模态振型可以识别结构的损伤状况。闫桂荣等[15]总结了三大类结构损伤识别方法：基于模态域的方法、基于时间域的方法以及基于小波变换时频域的方法。严平等[16]提出了一种基于单元模态应变能和小波变换的结构损伤识别方法，在单元模态应变能基础上,利用小波变换系数的变化和分布情况构建单元模态应变能小波变换的结构损伤指标，准确识别出了结构的损伤位置以及损伤程度。目前，国内外学者已经研究了多种高精度、高效率的结构损伤识别方法，但是对于能同时识别结构损伤时间、位置以及程度的方法的研究依然匮乏。

基于时频特征的结构损伤识别不仅可以识别结构损伤的位置和损伤程度，而且可以识别结构损伤发生的时间，特别适合于广泛实施的实时健康监测系统。因此，本文提出了一种基于时变模态振型小波变换的结构损伤识别方法，利用小波变换先识别出结构的时变模态参数，然后对识别的时变振型差做小尺度的小波变换，通过小波系数的实部出现极大值的时间及其出现的位置识别出结构的损伤时间与损伤位置，通过极大值的大小判断损伤程度，应用于悬臂梁结构以及昌赣客运专线赣江特大桥模型中，均成功识别出结构的损伤。

1 基本理论

小波变换是一种窗口大小固定但形状可变，时域和频域分辨率都可改变的时频局部化分析方法。它可以对非稳态信号和非线性结构进行详细的时频分析和多分辨分析，已经成为分析时变结构模态参数的重要方法。

1.1 小波变换原理

设ψ(t)∈L2(R)(L2(R)为平方可积的实数空间，即能量有限的信号空间)为小波母函数，且ψ(t)满足可容许条件

(1)

式中，ψ(ω)为小波母函数ψ(t)的傅里叶变换。将小波母函数通过伸缩和平移可以得到小波函数族

(2)

式中：a为尺度参数，可以控制小波母函数的伸缩；b为平移参数。

本文使用复Morlet小波作为小波母函数，其表达式为

(3)

式中：fb为带宽参数；fc为小波的中心频率，实际应用中，可以通过修改这两个参数来达到精度的要求。复Morlet小波的频域表达形式[17]为

(4)

对于任意信号x(t)，其连续小波变换可表示为

(5)

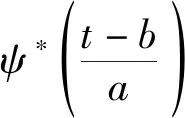
1.2 基于小波变换的瞬时模态参数识别方法

单自由度黏性阻尼系统的脉冲响应函数可以表示为

x(t)=Be-ζωntcos(ωdt+φ0)

(6)

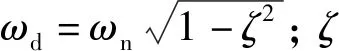
xa(t)=x(t)+jH[x(t)]=Be-ζωntej(ωdt+φ0)

(7)

式中，H[x(t)]为x(t)的希尔伯特变换，将式(7)代入式(5)，并将Be-ζωnt在t=b附近泰勒展开得

(8)

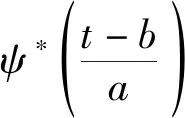
(9)

多自由度黏性阻尼系统的脉冲响应函数可以表示为

(10)

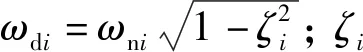
同理，将式(10)代入式(5)，泰勒展开并忽略无穷小量可以得到

(11)

1.2.1 基于小波系数模极大值的瞬时频率识别方法

对于单自由度黏性阻尼系统，设响应信号的采样频率为fs，代入式(6)可得

(12)

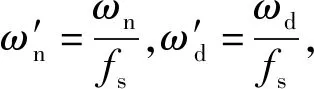
(13)

本文使用的是复Morlet小波，将复Morlet小波母函数代入式(13)，并对小波系数取模可得

(14)

由式(14)可知，在时刻k=b，当尺度参数a满足aω′d=2πfc时，小波系数的模能取最大值。因此，在时刻k=b，只要找到能使小波系数模取最大值的尺度参数al，即可得到这一时刻的瞬时频率为

(15)

因此，对于每个时刻，找到使小波系数模取最大值的尺度参数al，即可得到信号的瞬时频率。

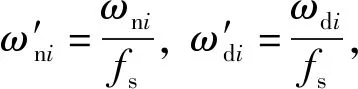
(16)

(17)

因此，在时刻k=b，只要找到能使小波系数模取第i个局部极大值的尺度参数ali，即可得到这一时刻的第i阶瞬时频率为

(18)

1.2.2 基于小波系数比值的瞬时振型识别方法

若一个结构有m个节点，假设：xp(t)为第p个节点的脉冲响应信号；xr(t)为第r个节点的脉冲响应信号。在尺度ali下对它们进行连续小波变换，由1.2.1节可知，当取aliω′di=2πfc时，多自由度系统就可解耦成只含第i阶模态的系统。因此，Wψ,p(ali,b)和Wψ,r(ali,b)都只保留了各自节点的第i阶模态振型。选取r节点为参照点，则在时刻t=bk，p节点相对于r节点的第i阶振型χi,p,bk可表示为[18]

χi,p,bk=Wψ,p(ali,bk)/Wψ,r(ali,bk)

(19)

因此，对每个节点信号都做同样的小波变换，然后进行归一化处理，即可得到结构在时刻t=bk的第i阶瞬时振型

Φi,bk=[χi,1,bk,χi,2,bk,…,χi,r-1,bk,1,χi,r+1,bk,…,χi,m-1,bk,χi,m,bk]

(20)

同理，其他任意时刻的瞬时振型都可以由式(19)和式(20)得到，则结构在任意时刻的第i阶振型为

(21)

式中：w为时间步数；m为节点数。因此，结构任意时刻的振型都可由式(21)得到。

1.3 基于时变振型差小波变换的损伤识别方法

结构损伤是一种非线性发展过程，将导致结构模态参数的时变特征。结构的振型包含了结构各个节点的信息，因此本文从结构时变振型入手，利用小波变换的奇异性检测能力和局部放大特性[19]，对结构第一阶时变振型差做小尺度的小波变换，通过变换后的结果来识别损伤。

对于一个含有m个节点的结构，假设结构损伤前的第一阶理论振型为

Φ1,0=[χ1,1,0,χ1,2,0,…,χ1,r-1,0,1,χ1,r+1,0,…,χ1,m,0]

(22)

结构在任意时刻的振型可由式(19)以及式(20)计算得到，则结构在时刻t=bk的第一阶振型差可以表示为

ΔΦ1,bk=[Δχ1,1,bk,Δχ1,2,bk,…,Δχ1,r-1,bk,0,Δχ1,r+1,bk,…,Δχ1,m,bk],

(23)

当结构发生损伤时，损伤位置的振型变化会大于其他位置的变化[20]。因此，利用本文复Morlet小波实部的奇异性检测能力和局部放大特性，对结构的振型差做小尺度小波变换

(24)

若结构在这个时刻(t=bk)有损伤，则小波系数实部出现极大值的位置即为结构损伤位置。

同理，任意时刻的第一阶振型差都可由式(23)得到，然后利用式(24)对振型差做小尺度小波变换，则小波系数的实部出现极大值的时间bk即为结构的损伤时间，出现极大值的位置即为结构损伤位置，极大值的大小反映了损伤的程度。

2 数值仿真

2.1 悬臂梁算例

通过一个1 m长悬臂梁数值模型，验证时变模态参数小波变换方法用于损伤识别的有效性。悬臂梁由10.0个单元组成，其模型示意图，如图1所示。

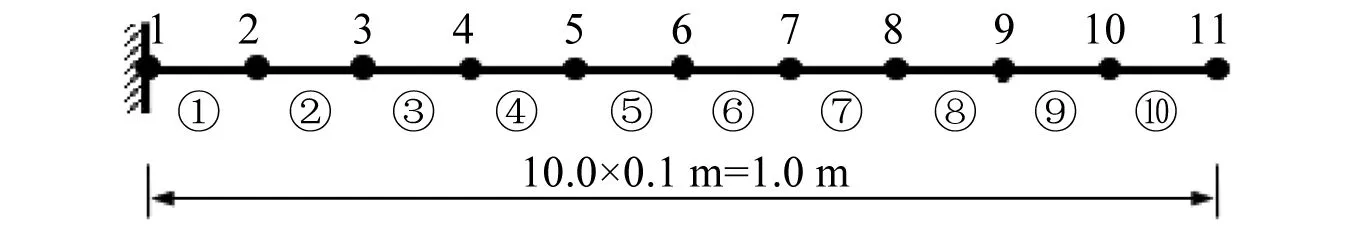
图1 悬臂梁结构模型Fig.1 The model of cantilever beam structure

结构在未损伤前，各个单元的抗弯刚度EI=4.73×103N·m2，抗拉刚度EA=1.42×106N，密度ρ=2 500 kg/m3。为了验证本文方法的精确性，在悬臂梁上施加了Imperial Valley地震波，地震波采样频率为200 Hz，如图2所示。

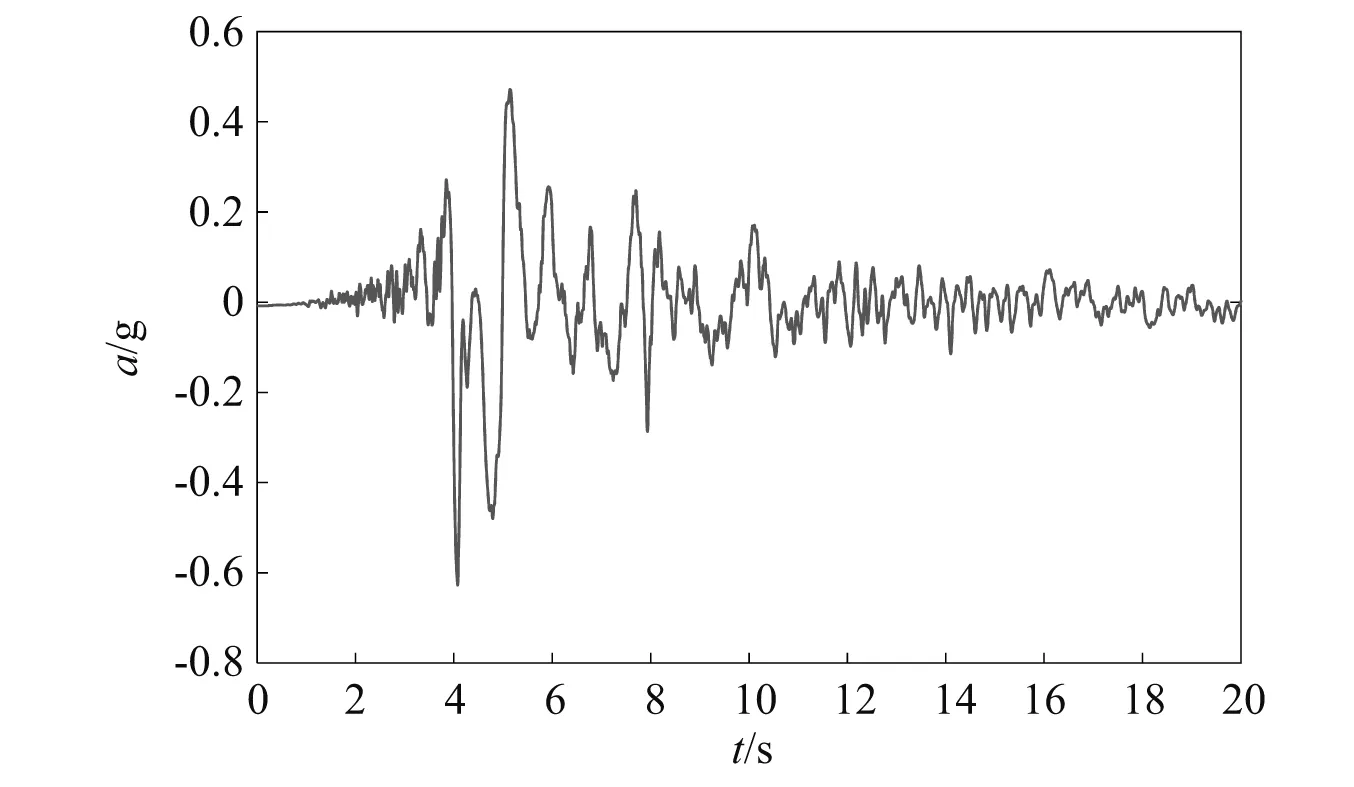
图2 Imperial Valley地震波加速度曲线Fig.2 Acceleration curve of seismic wave in Imperial Valley

本文通过刚度改变模拟结构非线性损伤，有利于定量损伤程度，通过减小单元弹性模量E的值模拟单元刚度损失。当结构施加如图2的地震波时，假设：当t=5 s时，结构的单元2发生了10%损伤；当t=10 s时，结构的单元3发生了5%损伤。因此，整个损伤过程可以分为3个阶段，如表1所示。

表1 悬臂梁损伤状况表Tab.1 Damage stage table of the cantilever beam

对于每个阶段，运用结构动力学知识，由弹性模量以及密度等参数计算结构的刚度矩阵和质量矩阵，从而可以得到结构每个阶段的第一阶理论频率为：f1=3.849 9 Hz，f2=3.797 0 Hz，f3=3.780 2 Hz。将节点11作为参照节点r，还可以得到每个阶段结构的第一阶理论振型，如图3所示。由图3可知：虽然结构在不同阶段有不同的损伤，但理论振型变化很细微，仅凭结构在3个阶段的振型变化难以识别结构损伤。

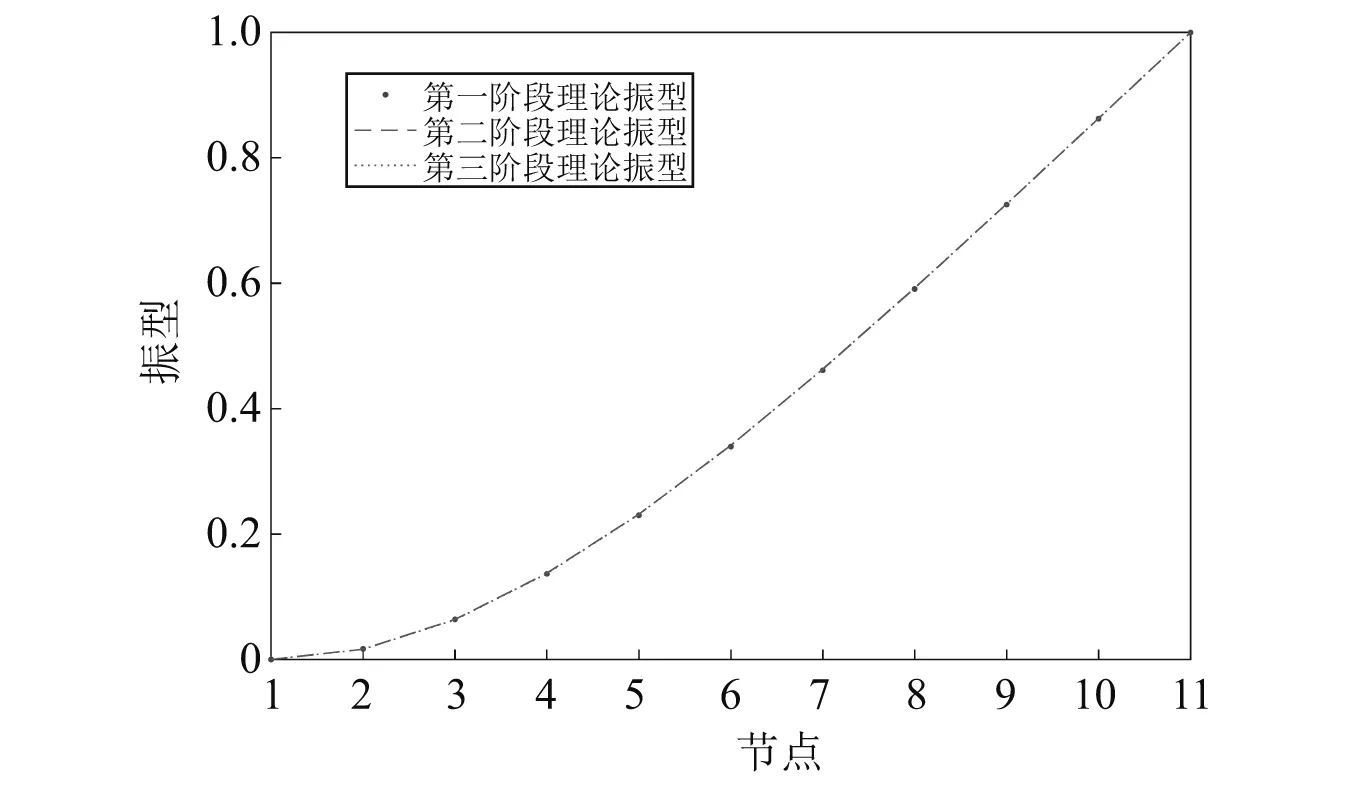
图3 悬臂梁第一阶理论振型Fig.3 The first theoretical mode shape of the cantilever beam

施加地震波后，结构每个节点的动力响应信号可以由Newmark法模拟得到。本文选取位移响应信号分析，节点11前20 s的原始位移响应，如图4所示。

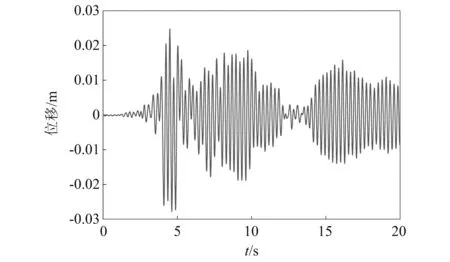
图4 节点11前20 s的位移信号Fig.4 The displacement signal for the first 20 s of node 11

2.1.1 瞬时频率与瞬时振型的识别

考虑到模拟损伤程度的大小和实际工程中噪声的影响，本文在原始位移响应中添加了1%的高斯白噪声，分别探究无噪声和有噪声环境下本文算法的有效性。使用复Morlet小波作为母小波，设置小波中心频率fc=3 Hz。将两种情况下节点11的位移信号作为x(t)代入连续小波变换。由1.2.1节可知，只要找到能使小波系数模取第i个局部极大值的尺度参数ali，即可得到这一时刻的第i阶瞬时频率。因此，通过提取每个时刻满足条件的尺度参数al1，代入式(18)，即可得到结构的第一阶瞬时频率，如图5所示。

由图5可知，无噪声识别结果比有噪声识别结果得到的曲线更加光滑。两种情况下，频率在t=5 s以及t=10 s时都发生了突变，说明结构在这两个时刻发生了损伤。时变频率分为3个阶段，0～5 s对应表1的阶段1，5～10 s对应表1的阶段2，10～20 s对应表1的阶段3。将每个阶段频率的平均值作为识别值，与理论值的对比如表2所示。

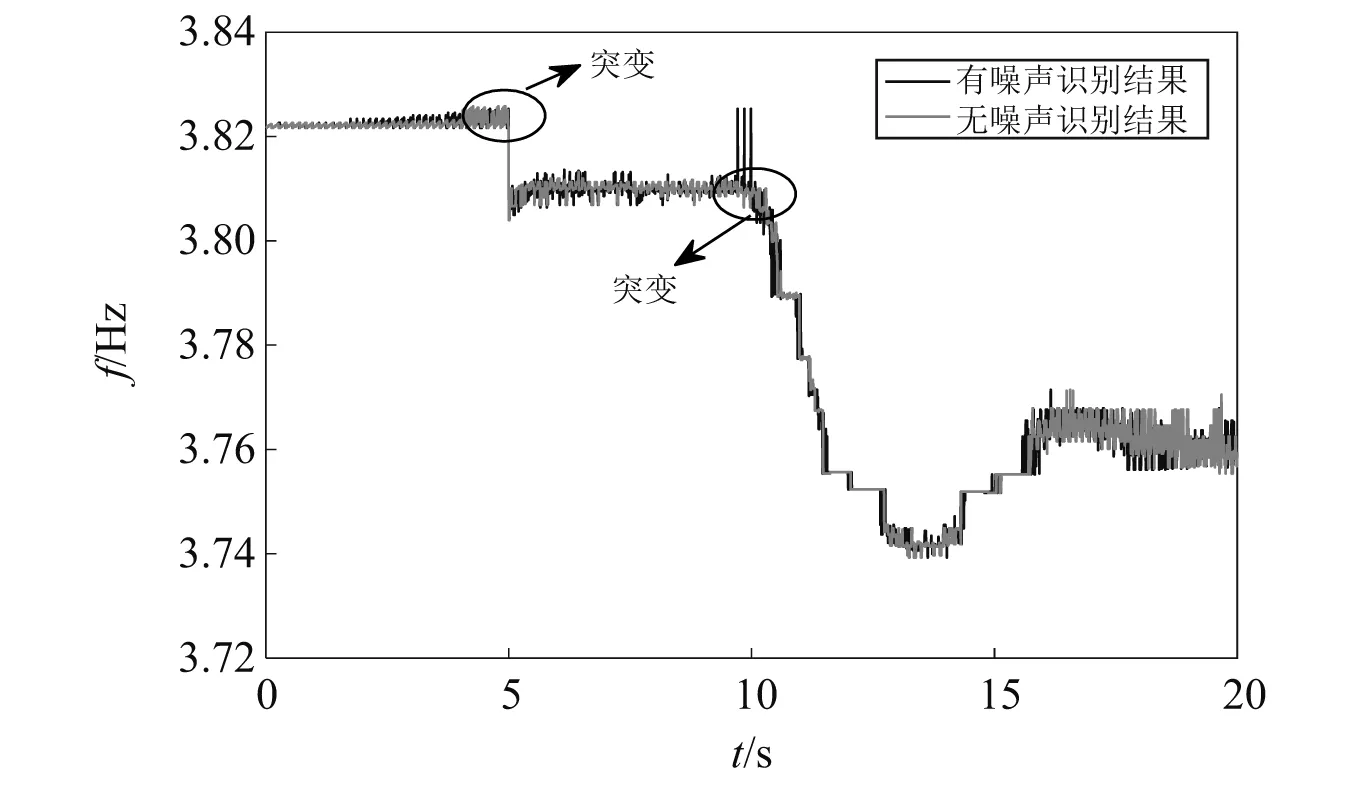
图5 悬臂梁第一阶瞬时频率Fig.5 First order instantaneous frequency of the cantilever beam

表2 悬臂梁频率对比表Tab.2 Frequency comparison table of the cantilever beam Hz

由表2可知，两种情况下，各个阶段第一阶频率的识别值与理论值很相近。进一步地，通过计算发现，两种情况下，各个阶段识别值与理论值的相对误差绝对值都在2%以下，说明本文小波变换方法能高精度地提取结构的瞬时频率，且具有一定的抗噪性。

在无噪声和有噪声这两种情况下，分别对每个节点的位移信号做同样的小波变换，并选取节点11为参照节点r，运用式(19)和式(20)即可计算结构任意时刻的第一阶瞬时振型，如图6、图7所示。

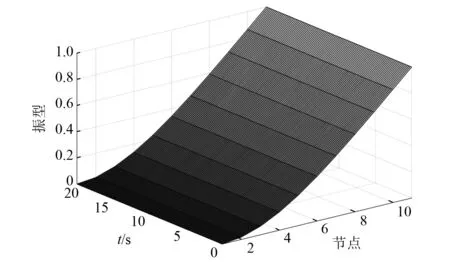
图6 无噪声下悬臂梁第一阶瞬时振型Fig.6 First order instantaneous mode shape of the cantilever beam without noise

由图6、图7可知，瞬时振型曲线与理论振型相似，并且通过计算，发现每个阶段识别的瞬时振型与对应阶段的理论振型的模态置信度(modal assurance criterion,MAC)值接近1，这说明通过小波变换方法能高精度地提取结构的瞬时振型。

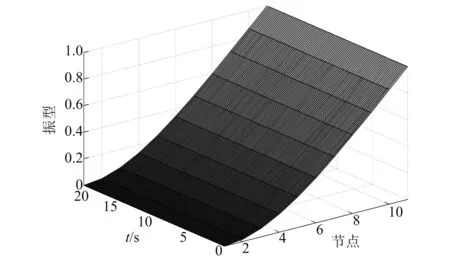
图7 有噪声下悬臂梁第一阶瞬时振型Fig.7 First order instantaneous mode shape of the cantilever beam under noise

2.1.2 损伤识别

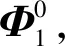
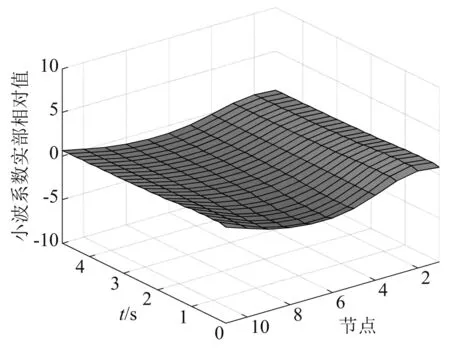
图8 无噪声下第一阶段损伤识别Fig.8 Damage identification of the first stage without noise

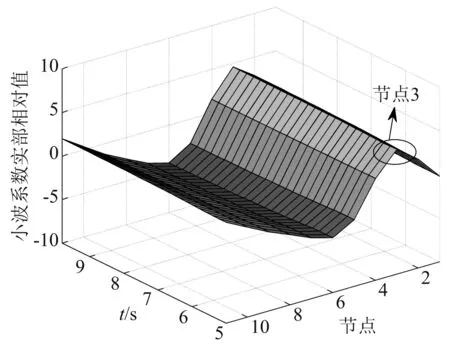
图9 无噪声下第二阶段损伤识别Fig.9 Damage identification of the second stage without noise

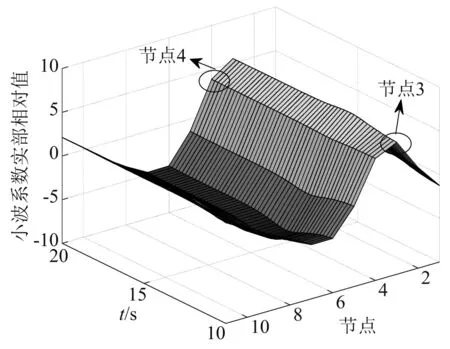
图10 无噪声下第三阶段损伤识别Fig.10 Damage identification of the third stage without noise

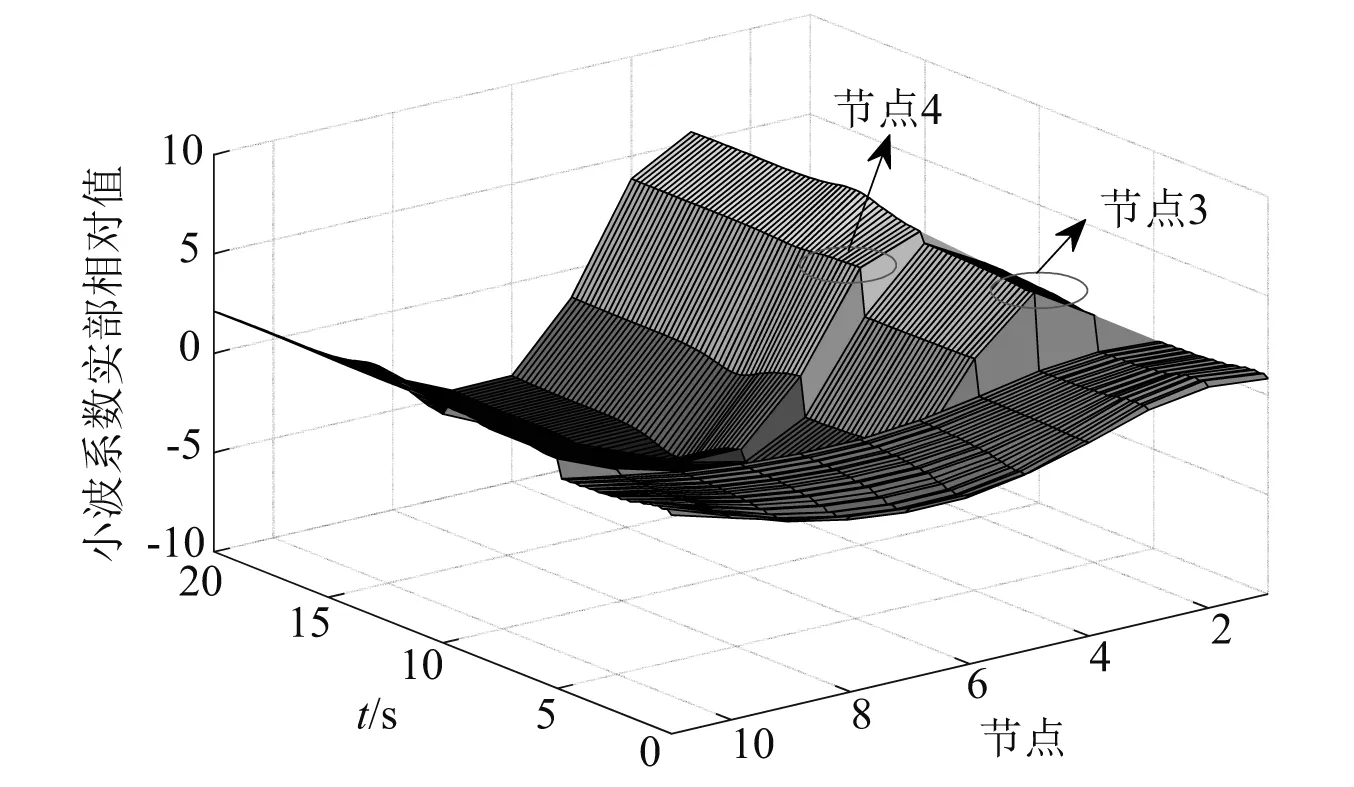
图11 无噪声下全过程损伤识别Fig.11 Damage identification of the whole stage without noise

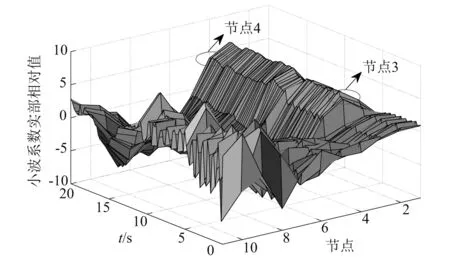
图12 有噪声下全过程损伤识别Fig.12 Damage identification of the whole stage under noise

由图8可知，没有极大值出现，说明在阶段1结构无损伤；由图9可知，在t=5 s之后，结构在节点3处(对应单元2)有极大值，说明在阶段2结构的单元2发生了损伤；由图10可知，在t=10 s之后，结构在节点3(对应单元2)和节点4处(对应单元3)均出现了极大值，说明阶段3结构的单元2、单元3都发生了损伤；由图11和图12可知，有噪声和无噪声环境下均能准确识别出损伤位置；由图8～图12可知，结构在t=5 s时，单元2发生损伤，在t=10 s时，单元2、单元3都发生损伤，识别的结果与表1中设置的刚度损失工况一样，说明本文方法能够精确的识别出结构的损伤时间和损伤位置，且具有一定的抗噪性。

由表1可知，在阶段2结构发生了单损伤，在阶段3结构发生了多损伤。在阶段2时，为了进一步判断损伤程度，依次设置单元2的损伤程度为10%，15%，20%，…，30%，用本文的方法依次提取每种损伤程度下振型差小波系数的实部相对极大值，如图13所示。

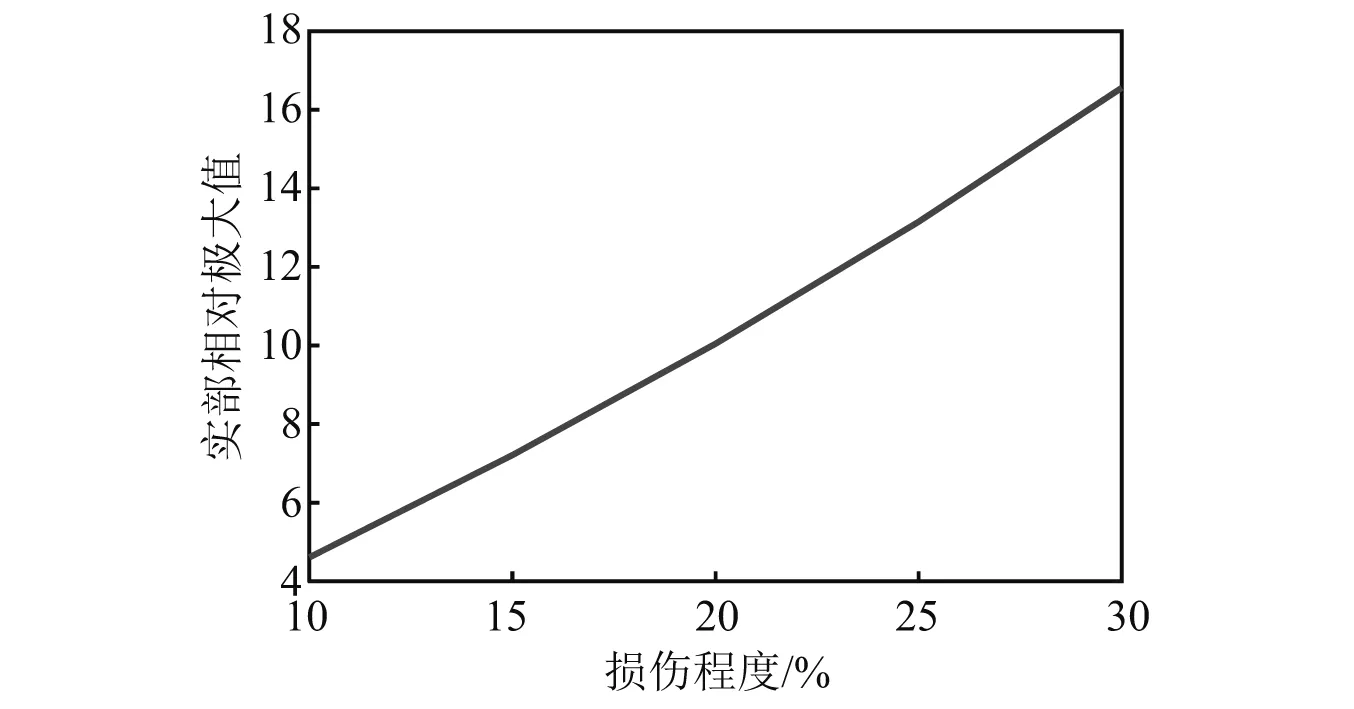
图13 不同损伤程度下单元2小波系数实部相对极大值Fig.13 The relative maximum value of the real part of the wavelet coefficients of unit 2 in different damage degree

由图13可知，实部相对极大值随着损伤程度的增大而增大，即可判断：单损伤下，振型差小波系数的实部相对极大值越大，单元的损伤程度越大。

阶段3结构发生了多损伤，为了进一步判断单元3的损伤程度，保持单元2的损伤不变(10%)，依次设置单元3的损伤程度为5%，10%，15%，…，30%，用本文的方法依次提取每种损伤程度下单元3振型差小波系数的实部相对极大值，如图14所示。

由图14可知，实部相对极大值随着损伤程度的增大而增大，即可判断：多损伤下，在其他单元不变的情况下，所求单元振型差小波系数实部相对极大值越大，该单元的损伤程度越大。

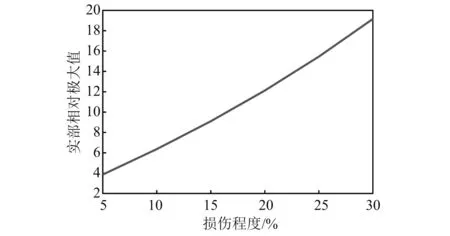
图14 不同损伤程度下单元3小波系数实部相对极大值Fig.14 The relative maximum value of the real part of the wavelet coefficients of unit 3 in different damage degree

综上所述，本文方法能够精确地识别出悬臂梁结构的损伤时间、损伤位置和损伤程度，且具有一定的抗噪性。

2.2 昌赣客运专线赣江特大桥算例

昌赣客运专线赣江特大桥(以下简称赣江桥)位于江西省赣州市，其主桥桥位位于章水、贡江两江汇合口下游1.9 km处，位于既有赣江公路大桥上游1.1 km处。主桥结构采用(35+40+60+300+60+40+35)m混合梁斜拉桥，半漂浮体系，全梁长572.1 m(含梁缝)。索塔全高分别为124.5 m，127.6 m，桥面以上塔高88 m，为主跨的1/3.409。斜拉索采用空间双索面体系，扇形布置，全桥共48对斜拉索。本文通过赣江桥实测响应数据不断进行有限元模型修正，得到了实际桥梁的等效模型，其有限元模型如图15所示。

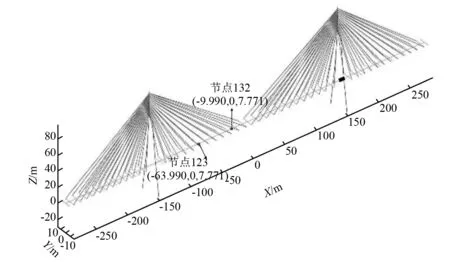
图15 赣江桥模型Fig.15 The model of Ganjiang River Bridge

桥梁的主跨由108个节点(节点81～节点188)以及107个单元(单元79～单元185)组成。根据美国国家公路与运输协会标准(AASHTO)对于船舶碰撞荷载提出的经验公式，船桥正撞时的设计船舶撞击力按式(25)计算

(25)

式中：P为撞击力；DWT为载质量吨位；v为船舶的速度。现实中，船桥碰撞时，相撞船舶周围水的质量对荷载也有影响，可以将这部分影响以船体附加质量的形式加以修正，即

DWT=m1+m2=(1+k)m1

(26)

式中：m1为船舶载质量吨位；m2为附加水质量；k为附加因子，一般取0.02～0.07，本文取0.05。

利用ANSYS软件模拟速度为6 m/s，质量为850 t的船撞向赣江桥的节点123(对应单元120)，由式(25)、式(26)可得冲击力为22 MN，使用ANSYS软件完成了船桥碰撞瞬态分析，并通过有限元模型修正方法获取了单元等效刚度损失为30%。为了便于定量损伤程度，本文通过设定碰撞后单元弹性模量折减30%证明本文方法的精度。通过设置标准差为0.01的白噪声激励信号模拟环境激励，当t=5 s时，通过22 MN荷载模拟碰撞冲击力，采样频率为50 Hz，由Newmark法模拟得到各个节点的动力响应，节点123碰撞前后10 s的位移响应信号，如图16所示。

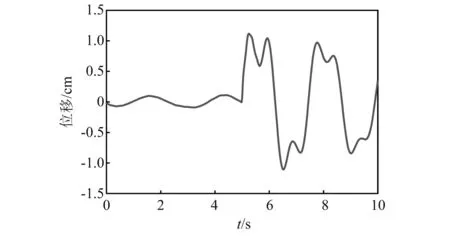
图16 节点123的位移信号Fig.16 The displacement signal of node 123

整个船桥碰撞过程分为两个阶段，如表3所示。当t<5 s时，结构为未损状态；当t≥5 s时，船桥碰撞，碰撞处发生了损伤。通过数值模型计算可以得到桥梁每个阶段的第一阶理论频率为：f1=0.414 1 Hz，f2=0.412 9 Hz。将节点132作为参照节点r(振型为“1”的节点)，进行归一化处理，还可以得到桥梁碰撞前后第一阶理论振型，如图17所示。

表3 “船撞桥”损伤状况表Tab.3 Damage stage table of “ship-bridge collision”

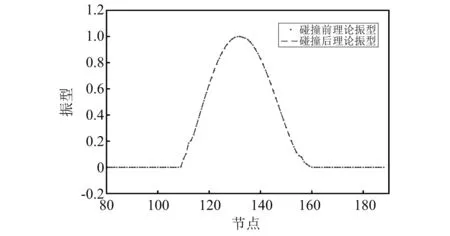
图17 桥梁碰撞前后第一阶理论振型Fig.17 The first theoretical mode shape before and after collision

由图17可知，虽然桥梁在碰撞后有损伤，但碰撞前后理论振型变化很细微，仅凭桥梁在碰撞前后振型变化难以识别桥梁损伤。

2.2.1 瞬时频率与瞬时振型的识别

使用复Morlet小波作为母小波，设置小波中心频率fc=5 Hz。将节点123的位移信号作为x(t)代入连续小波变换。找到每个时刻满足极大值条件的尺度参数al1，代入式(18)，即可得到结构的第一阶瞬时频率，如图18所示。

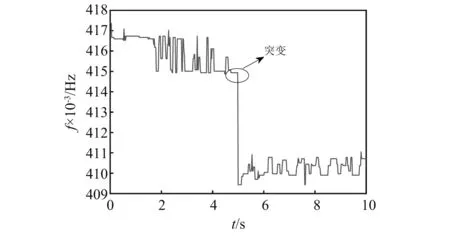
图18 赣江桥第一阶瞬时频率Fig.18 First order instantaneous frequency of Ganjiang River Bridge

由图18可知，频率在t=5 s时发生了突变，说明结构在这个时刻发生了损伤。时变频率分为两个阶段，0～5 s对应表3的阶段1，5～10 s对应表3的阶段2，将每个阶段频率的平均值作为识别值，与理论值的对比如表4所示。

表4 赣江桥频率对比表Tab.4 Frequency comparison table of Ganjiang River Bridge

由表4可知，第一阶频率的识别值与理论值相对误差绝对值非常小，各个阶段的误差都在2%以下。充分说明了小波变换方法识别瞬时频率的精确性。

对每个节点的位移信号做同样的小波变换，并选取节点132为参照节点r(振型为“1”的节点)，运用式(19)和式(20)可计算赣江桥任意时刻的第一阶瞬时振型，如图19所示。由图19可知，瞬时振型曲线与理论振型相似，并且通过计算，发现每个阶段识别的瞬时振型与对应阶段的理论振型的MAC值接近于1，这说明通过本文小波变换方法能高精度地提取赣江桥的瞬时振型。

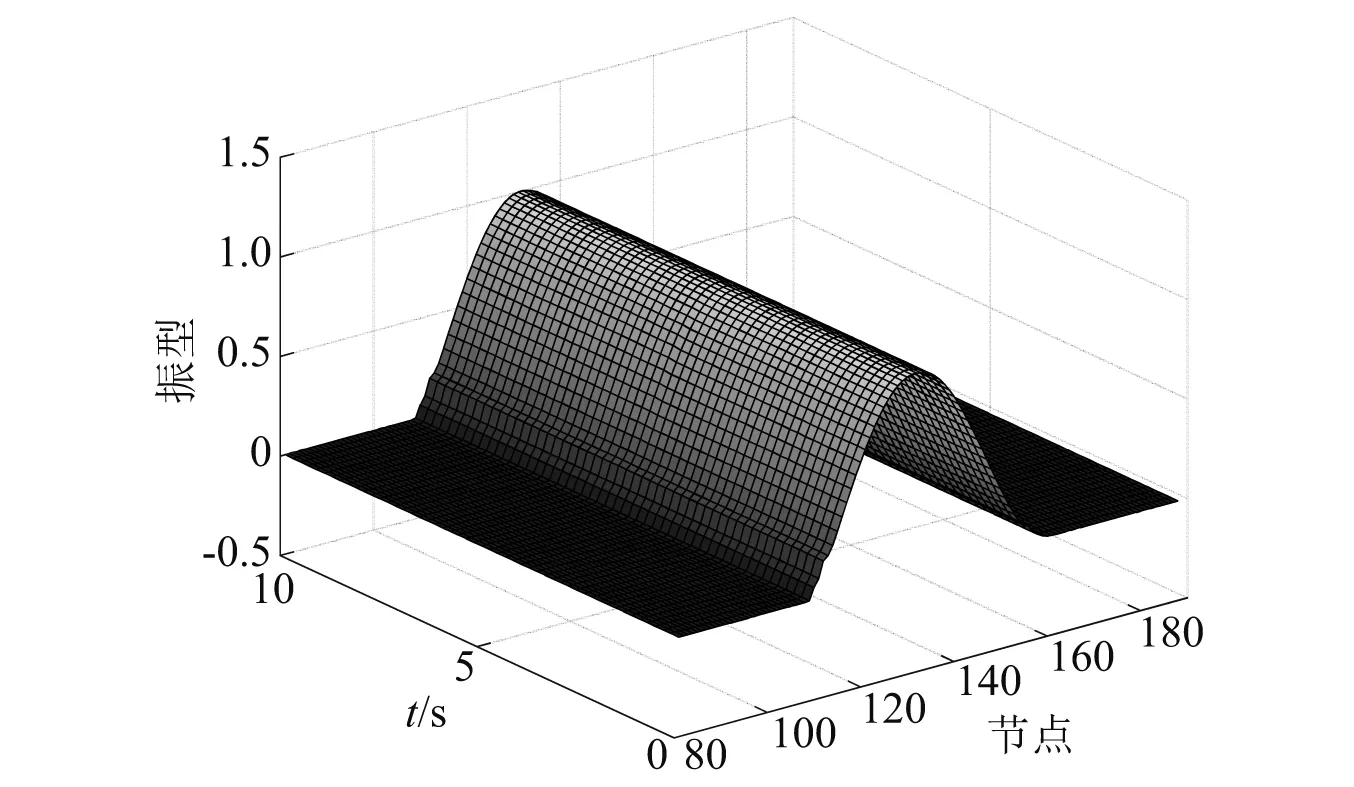
图19 赣江桥第一阶瞬时振型Fig.19 First order instantaneous mode shape of Ganjiang River Bridge

2.2.2 损伤识别

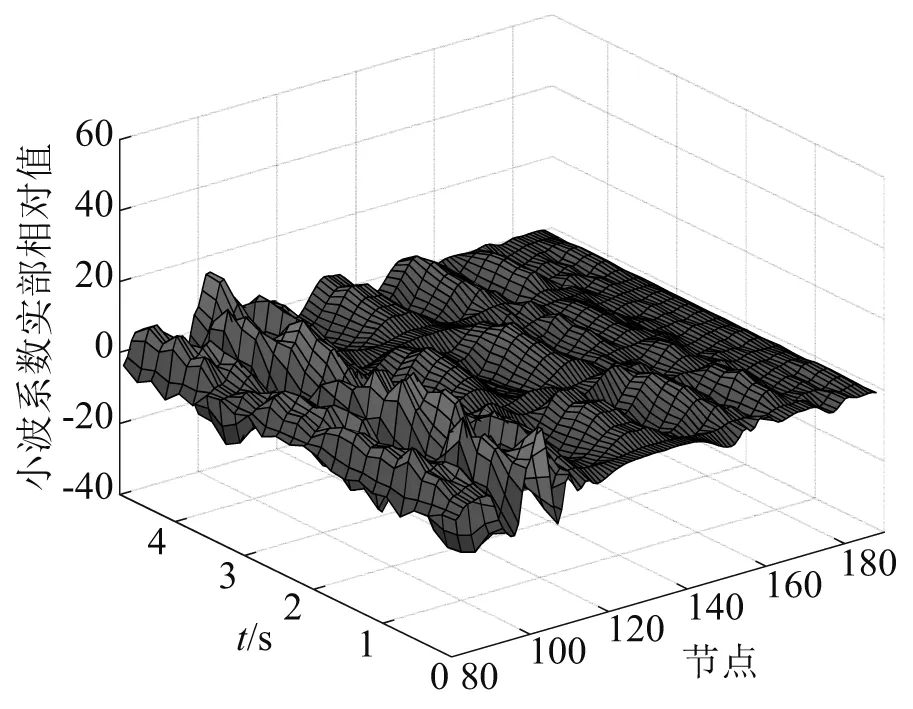
图20 碰撞前损伤识别Fig.20 Damage identification before collision

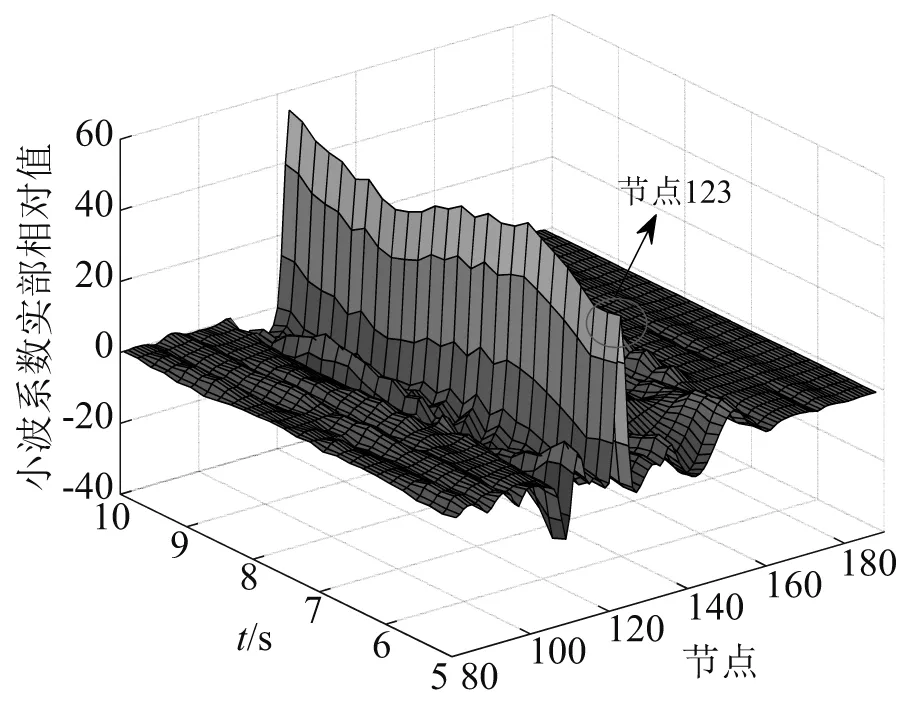
图21 碰撞后损伤识别Fig.21 Damage identification after collision

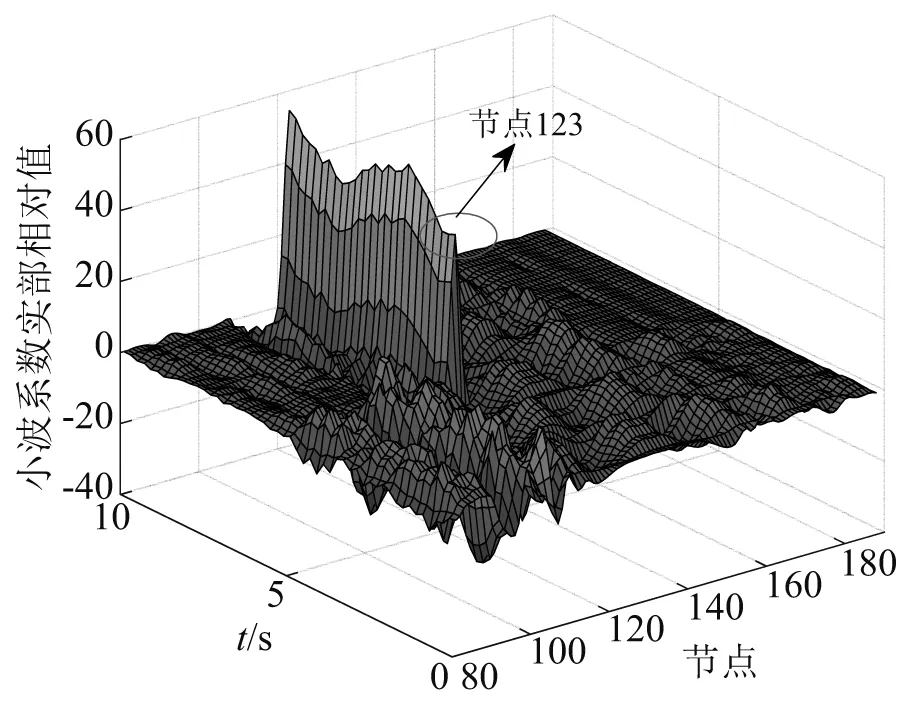
图22 全过程损伤识别Fig.22 Damage identification of the whole stage

由图20可知，当t=0～5 s时，没有极大值出现，说明在这一阶段桥梁无损伤；由图21可知，当t=5～10 s时，桥梁在节点123处(对应单元120)有极大值，说明在这一阶段桥梁的单元120发生了损伤。因此，可以判断当t=5 s时，发生了“船撞桥”事件，且撞击的位置为单元120，识别的结果与损伤状况吻合，说明本文方法能够精确地识别出船桥碰撞的时间和位置。

3 结 论

(1)本文提出了一种基于时变模态振型小波变换的结构损伤识别方法。通过提取当小波系数模取极大值时的尺度参数，识别出结构的瞬时频率。然后选取特定尺度参数，对结构各个节点的信号进行连续小波变换，从而将信号解耦到只含某阶模态，通过小波系数的比值进行归一化处理，从而得到结构的瞬时振型。最后，对结构第一阶时变振型差做小尺度的小波变换，通过小波系数的实部出现极大值的时间及其出现的位置识别出结构的损伤时间与损伤位置，通过极大值的大小判断损伤程度。

(2)将该方法应用于一个地震波作用下的悬臂梁结构中，结果表明，该方法不仅能准确地识别出结构单损伤、多损伤发生的时间，还能准确地识别出损伤的位置以及损伤程度。

(3)将该方法应用于一个冲击荷载作用下的“船撞桥”事件模拟。结果表明，该方法不仅能够精确地识别出船桥碰撞的时间，并且能够准确地识别出碰撞位置。