高精度角分度转台设计及其误差修正研究*

李忠明,李俊霖,韩 冰,唐延甫,杨永强

(1.中国科学院 长春光学精密机械与物理研究所,吉林 长春 130033;2.中国科学院大学,北京 100049)

0 引 言

高精度转台在光电测试、航空航天及精密仪器等许多领域有着广泛的应用。高精度转台的测角精度直接影响系统的整体性能。同时,随着科学技术的发展,各类高精度转台的应用场合对其转台角分度精度的要求也越来越高[1-3]。

在高精度转台设计中,常用的动力传动形式有直驱、蜗轮蜗杆传动和齿轮传动等[4,5]。其中,蜗轮蜗杆传动承载能力大,经济性好,但是空回对传动性能有一定的影响。轴承常采用气浮轴承、密珠轴承、转台轴承、球轴承组等[6,7],其中转台轴承在性能、成本、空间等方面的综合比较下具有较大的优势,单个轴承便可以承受径向载荷、轴向载荷及力矩载荷,安装使用方便、旋转精度高。

高精度转台常采用圆光栅作为角度编码器。转台的角分度精度主要受转台轴系精度、圆光栅测量精度的影响。轴系精度与零件制造、安装及轴承性能有关,提高轴系精度,有利于提高转台的角分度精度[8]。圆光栅的测角精度受诸多因素影响,如圆光栅的安装偏心、倾斜、变形等安装因素,还有圆光栅制造时的刻线误差和电子细分误差等,其中,安装因素对圆光栅测角精度影响比较大[9,10]。

针对圆光栅安装导致的测角误差,有硬件补偿和数值补偿两类方法。

(1)在硬件补偿方面,文献[11]采用四读数头对称布置,采用基于遗传算法的参数优化算法,建立了误差模型来进行误差补偿。文献[12]提出了一种利用双读数头平均误差补偿方法,圆光栅的测角精度有较大的提高;但是硬件补偿对读数头的安装位置要求比较高,成本也较大。

(2)在数值补偿方面,文献[13]利用谐波分析方法来建立误差补偿函数,修正了圆光栅安装偏心导致的测角误差。文献[14]提出了一种确定圆光栅安装偏心量和方向的方法。文献[15]利用多体系统理论,建立了测角误差模型，进行了误差修正。

综上所述,数值补偿的方法大部分是修正圆光栅安装偏心导致的误差,而针对圆光栅安装变形的误差修正目前却鲜有报道。

为此,笔者设计一种蜗轮蜗杆传动的高精度转台,根据标定后得到的误差分布规律,提出一种基于查表法的角分度误差修正方法,并分别采用多齿分度台和十七面体对其误差修正效果进行验证。

1 转台结构设计

该转台主要由:蜗轮蜗杆组件、圆光栅、交叉滚柱轴环、电机等组成,转台结构的实物图如图1所示。

图1 转台内部实物图

此处,笔者根据《机械设计手册》[16]确定蜗杆的模数为2 mm,蜗杆分度圆直径为22.4 mm,传动比为1∶180,涡轮的分度圆直径为360 mm,中心距为191.2 mm。

此处,角度编码采用圆光栅来进行,其主要技术参数如表1所示。

表1 圆光栅主要技术参数

圆光栅安装在旋转轴上,直接检测旋转轴的转动角度,避免了蜗轮蜗杆空回对转台角分度精度的影响;圆光栅采用锥面安装形式,有一定的自定心效果,同时利用螺钉的顶拉来调整圆光栅的位置状态;圆光栅采用英国雷尼绍公司的RESM系列增量式圆光栅;电子细分误差远小于刻线误差及安装误差,可以忽略不计[17]。

交叉滚柱轴环采用THK公司的RU型产品,该型号是内外环一体式,使用简便,安装状态对性能几乎没有影响,因此能够获得稳定的旋转精度;交叉滚柱轴环内环固定在转台底板上,外环与旋转轴及蜗轮连接,精度等级选用P4级,较好的轴承精度有助于提高转台的角分度精度。

蜗轮蜗杆组件的传动比是1∶180,电机采用高分辨率型五相步进电机,基本步距角0.36°,200倍细分后理论步距角0.001 8°,经蜗轮蜗杆传动后转台旋转轴的运动分辨率0.036″。

2 转台仿真分析

在实际使用过程中,振动及形变会对高精度转台的测角精度及正常使用产生一定的影响,需要对其进行模态分析及静力学分析,并且考察转台的实际使用情况。

笔者使用ANSYS软件对转台载物台面进行仿真分析。其中,台面的变形分析如图2所示。

转台的应力分析如图3所示。

图3 转台应力分析

转台的变形分析如图4所示。

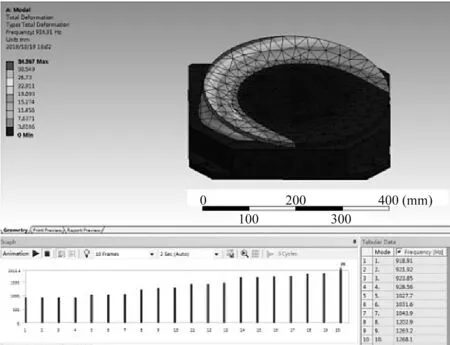
图4 转台模态分析

台面选用2A12铝合金,抗拉强度为410 MPa,屈服强度为265 MPa。

在实际使用时,转台的最大负载不超过15 kg,故笔者对转台载物台面施加150 N的力。通过仿真分析可知,载物台面的最大变形为0.003 7 mm,最大应力为1.97 MPa,二者均远小于材料的强度极限。

3 标定及误差补偿

转台标定的原理示意图如图5所示。

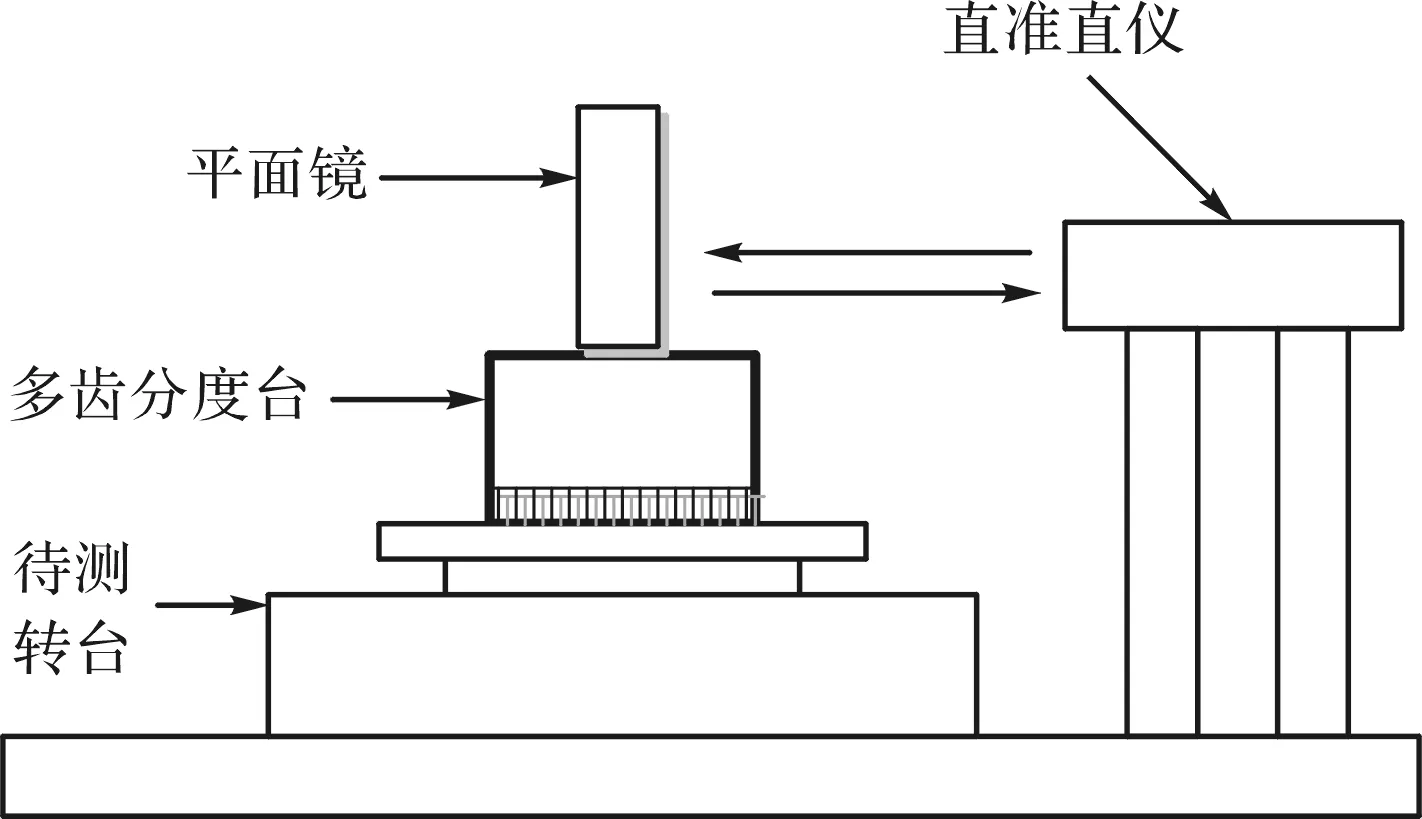
图5 转台标定原理图

转台标定的实物布局图如图6所示。

图6 转台标定布局图

转台标定的具体步骤如图7所示。

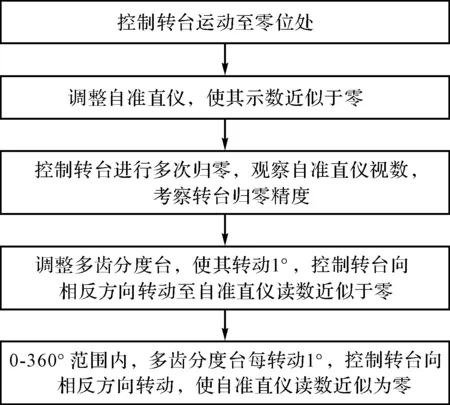
图7 转台标定步骤

接下来,笔者利用多齿分度台和自准直仪对转台进行具体的标定。

笔者将多齿分度台固定于转台台面的中心,由于两者的偏心会对标定的精度产生干扰,此处需要保证多齿分度台与转台旋转中心的同轴度[18];多齿分度台上放置反射镜,自准直仪与反射镜对准;当转台位于零位处时,调整自准直仪,使其视数近似为零。

当误差未修正时,由标定得到的最大测角误差是32.12″。

转台归零精度如表2所示。

表2 归零精度

转台的零位采用光电开关实现。转台的归零精度对于数值误差修正法至关重要,归零精度高,则数值误差修正方法的效果好。

首先,笔者考察转台的归零精度,转台位于零位时,自准直仪的度数为0.2″,控制转台进行5次重复归零,自准直仪的读数如表2所示,转台的归零最大误差不大于0.5″,具备较好的归零精度。

通过图7的标定步骤4,转台每次转过的角度与1°的差值,即是此位置的角分度误差,进而可以得到1°～360°范围内360个整度数位置的角分度误差。

转台的角分度误差分布情况如图8所示。

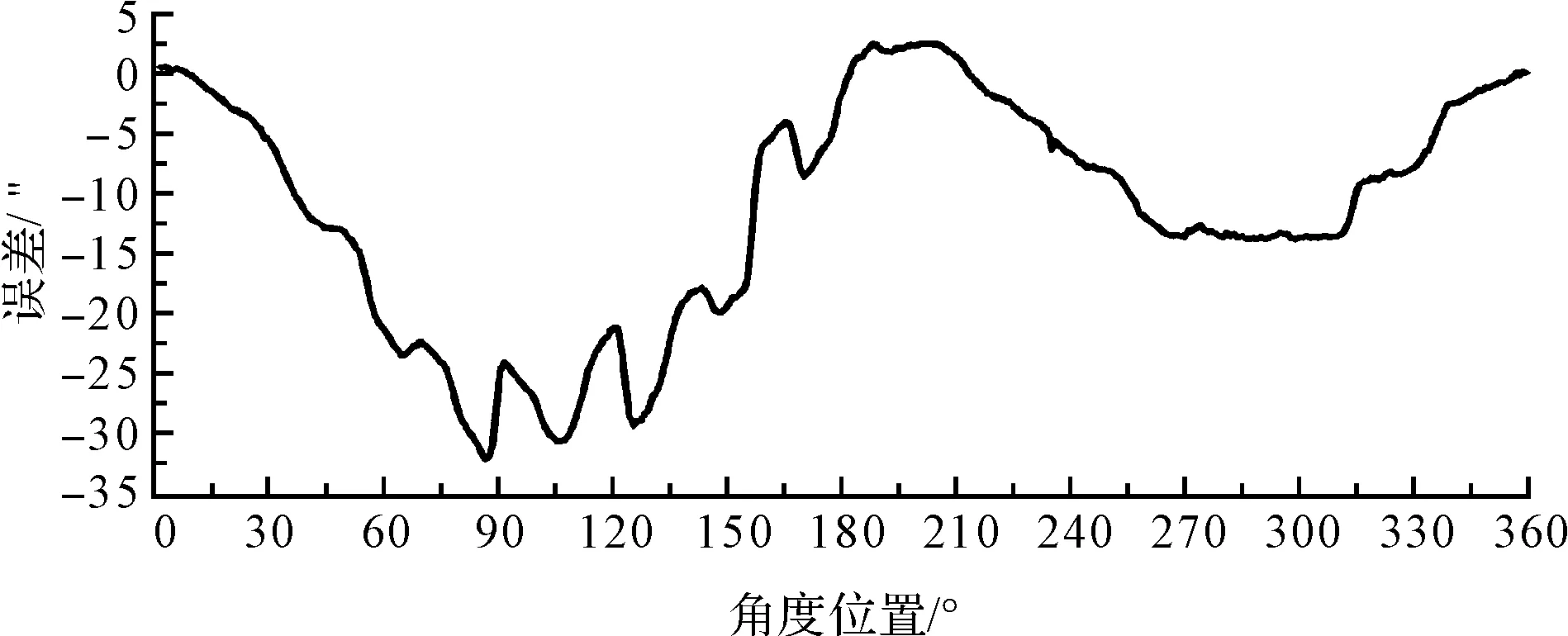
图8 转台角分度误差

根据360个角度位置的误差分布情况,结合圆光栅各种安装不当所导致的误差分布特点,可知圆光栅的变形对角分度精度的影响更明显,无法使用谐波分析等偏心误差修正方法来进行误差修正。

笔者采用查表法来进行误差修正,根据0～360°范围内360个整度数位置的误差,建立误差修正量的数表;利用相邻度数间的误差进行线性插值，得到了整度数之间的修正量,从而形成了完整的0～360°之间的误差修正量数表。

误差修正后的角分度误差分布情况如图9所示。

图9 转台角分度误差

4 实验验证

为了验证查表法的误差修正效果,笔者将0°～360°范围完整的误差修正量数表映射到DSP28377控制器中,即将360个整度数误差修正量写到DSP28377控制程序中,整度数位置的修正量可以直接使用,整度数之间的修正量利用相邻整度数修正值线性插值得到。

DSP28377控制器向转台发出目标角度位置时,需加上该角度位置的误差修正量,转台按照修正后的角度位置运动,运动完成后,控制器将转台返回的角度值减去误差修正量,便是真实的目标角度位置。

笔者利用多齿分度台和自准直仪对0°～360°范围内的360个整度数位置进行误差修正效果验证。由获得的数据可知,整度数位置的误差最大值为0.79″,误差修正效果显著。

笔者利用多齿分度台和自准直仪对转台进行标定,考察整度数位置的误差修正情况;无法考察整度数之间的,利用线性插值得到误差补偿量。由于十七面体的每个面对应的度数都不是整度数,笔者采用十七面体和自准直仪来进一步考察转台的角分度误差修正情况。

利用十七面体和自准直仪标定转台的实物图如图10所示。

图10 转台标定布局图

标定数据如图11所示。

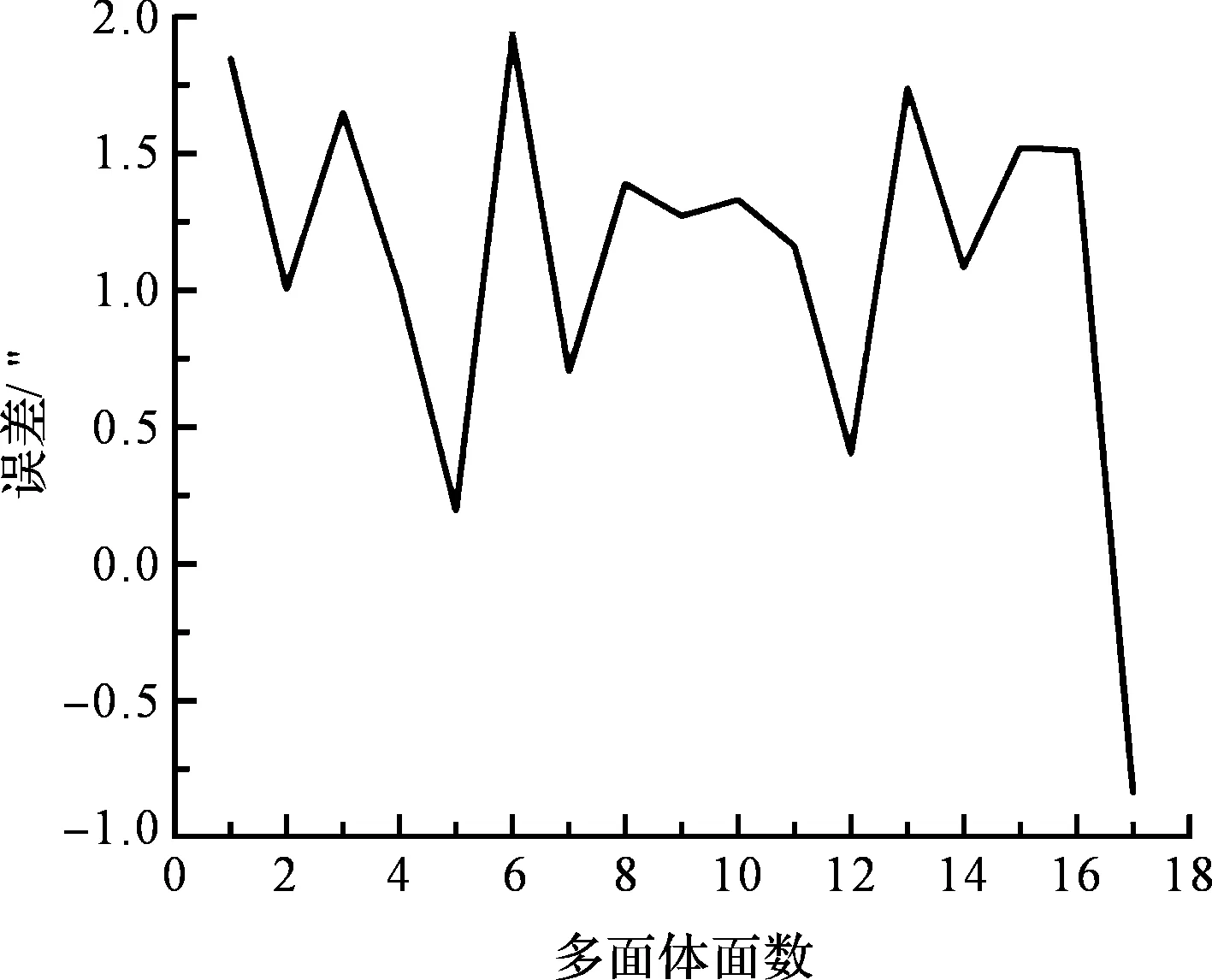
图11 转台角分度误差

十七面体安装在转台台面上,笔者利用千分表保证十七面体与转台旋转轴同心。

由图11可知转台角分度最大值为1.95″,可见整度数之间的误差修正效果也比较好。

5 结束语

本文提出了一种高精度角分度转台及其测角误差修正方法。转台采用蜗轮蜗杆传动、圆光栅测角的形式,圆光栅采用增量式,轴承采用交叉滚子轴环;利用自准直仪和多齿分度台对转台的测角误差进行标定;并分别利用多齿分度台和十七面体对误差修正效果进行验证。

研究结果表明:

(1)通过仿真分析,验证了设计的高精度转台满足静力学性能和模态特征满足使用要求;

(2)提出的利用自准直仪和多齿分度台的转台测角误差标定方法,可以得到0～360°范围内360个整度数位置的测角误差;

(3)转台测角误差分布无明显规律,提出的一种基于查表的转台测角误差修正方法,修正前后,最大测角误差分别为32.12″和1.95″,误差修正效果比较好。

在后续的研究中,笔者将针对圆光栅局部形变导致的测角误差分布规矩具有分段谐波分布的特点,对基于分段数学模型的误差修正方法进行更进一步的研究。