基于全闭环控制技术的滚珠丝杆伺服系统研究*
2021-09-27霍晓锐赵现朝石继超黄孟杰
霍晓锐,赵现朝,石继超,黄孟杰
(上海交通大学 机械与动力工程学院,上海 200240)
0 引 言
滚珠丝杆机构是数控加工设备中的常用机构,除了可以应用在进给平台的运动外,还可应用于各种并联机构和混联机构的运动支链当中。
目前,为了保证运动支链的运动精度,高端机床通常采用的是以光栅尺作为位置反馈元件的全闭环的控制策略。这种方式虽然能够直接测量执行机构的位置,避免由于机械间隙等带来的稳态误差;但是由于从电机的输出端到执行机构之间引入了更多的摩擦和机械间隙等非线性因素,系统的动态特性变差。
全闭环系统中存在最突出的两个问题是:(1)由于摩擦导致的爬行现象;(2)由于机械间隙在反向运动时产生的平顶现象,需要设计相应的模块进行补偿。基于摩擦模型的补偿方式是目前常用的摩擦补偿方式之一[1]。这种补偿方式的关键在于摩擦模型的选择以及摩擦参数的确定。早期的摩擦模型主要集中在静态摩擦模型,包括Coulomb模型[2]、Bingham模型[3]以及Stribeck模型[4]等。这类模型虽然能够比较精确地描述速度稳态时的摩擦力变化,但却无法描述预滑移阶段的动态特性。
直至近几十年,动态摩擦模型的出现使得系统在低速、小位移状态下的摩擦力可以得到较为精确的描述,比较著名的模型有Dahl模型[5]、Leuven模型[6]以及LuGre模型[7]等等。其中,Lugre模型凭借其模型简单、描述精确[8]等特点得到了广泛的应用。而采用LuGre模型的难点在于4个静态参数以及两个动态参数的确定。粒子群算法是确定系统摩擦参数的常用方法之一,该方法的原理简单、易于实现,但是传统粒子群算法容易陷入局部极值[9],精度很难提升。
目前,针对机械间隙的补偿研究主要停留在系统精度的补偿上。对于全闭环系统,系统精度可以通过光栅尺的直接测量得到保证。但是由于间隙的存在,系统在反向运动时会产生短暂的电机转动,而负载位置不变的现象,这种现象在位置-时间图中体现为折返处的“平顶”,影响了运动机构的位置响应特性。
本文以数控机床中的滚珠丝杆伺服系统为研究对象,针对LuGre模型,提出一种改进的混沌粒子群算法进行参数辨识,提升辨识精度;并针对摩擦与机械间隙这两个全闭环控制中的非线性问题,提出一种基于摩擦补偿和折返速度补偿的混合控制策略;最后通过实验来验证该控制方法的有效性。
1 基于LuGre模型的摩擦补偿
1.1 系统摩擦建模
滚珠丝杆传动机构具有刚度大、精度高、可靠性强等特点,一直被用作数控系统中旋转运动转化为直线运动的解决方案。
滚珠丝杆传动系统的机构简图如图1所示。

图1 滚珠丝杆传动系统
分析传动系统可知,系统的摩擦主要来源于4个方面:丝杆两端轴承内部的摩擦、丝杆负载与丝杆之间的摩擦、丝杆负载与导轨之间的摩擦、伺服电机内部的摩擦。这4种产生摩擦的要素中,丝杆负载与导轨之间的摩擦以及伺服电机内部的摩擦所占的比重较大,尤其是在负载加大时,由于工作台与导轨之间的预紧力加大,此时摩擦力对系统的影响会进一步增大。
本文中采用LuGre模型对系统中的摩擦进行描述,该模型能够较全面地描述摩擦的动静态特性,其数学表达式为:
(1)
式中:z(t)—接触面鬃毛的平均弹性形变量;ω(t)—输出轴角速度;σ0—鬃毛刚度系数;g(ω)—有界正函数;Tc—库伦摩擦力矩;Ts—最大静摩擦力矩;ωs—Stribeck角速度;Tf—总摩擦力矩;σ1—微观阻尼系数;σ2—粘滞摩擦系数。
在上述表达式中,σ0,Tc,Ts,ωs称为静态参数;σ1,σ2称为动态参数。可以看出,LuGre摩擦模型是一组相对复杂的带有微分方程的非线性函数,按照传统方法所确定的评价函数容易存在多个局部极值点,为摩擦参数的精确辨识带来困难。本文提出一种改进混沌粒子群算法(improved chaos particle swarm optimization, ICPSO),可以有效地避免陷入局部极值,并提升其辨识的精度。
1.2 改进混沌粒子群算法
混沌变量指的是由确定性的方程得出的具有随机性运动状态的变量。Logistic方程就是一个典型的,可以通过初始值迭代出混沌序列的方程:
zn+1=μzn(1-zn),n=0,1,2,…
(2)
式中:μ—控制参量,0<μ≤4;zn—混沌序列的第n项。
一旦控制参量μ的大小确定,由任意初值z0∈[0,1],可以迭代出混沌序列z1,z2,z3,…。混沌序列是一串同时具有随机性和遍历性[10,11]的序列。
随机性指混沌序列中的混沌变量有类似于随机变量的杂乱特性;遍历性指混沌序列可以不重复地遍历空间中的所有状态。而混沌优化[12,13]就是利用了混沌序列的遍历性,可以将粒子从理论上投放到搜寻空间的任意位置,增强粒子的随机性,实现全局最优。
粒子群算法(particle swarm optimization,PSO)由Kennedy和Eberhart于1995年提出[14],具有简单易行、收敛速度快、设置参数少等优点。首先笔者假设一个由N个粒子组成的群体,其中,第i个粒子的位置坐标为xi=(xi1,xi2,…,xin),n—解空间的维数。粒子群中每一个粒子的位置坐标都表示了一组潜在的参数解。将xi代入优化目标函数J(x)中就可以得到第i个粒子的适应度J(xi)。通过比较各个粒子的适应度大小就可以确定出当前粒子群经历过的最好位置gb=(g1,g2,…,gn),以及各个粒子所经历过的最好位置pbi=(pi1,pi2,…,pin),i=1,2,…,N。
传统粒子群算法的迭代公式如下:
(3)
(4)

但是传统的PSO算法无法解决早熟收敛与收敛精度之间的矛盾。
迭代公式中的惯性权重值w具有以下特点:大惯性权重值有利于粒子脱离局部极值,小惯性权重值有利于粒子收敛,提升精度[15]。
本文采用分阶段的方式,将粒子群算法的整个迭代过程分为3个阶段:
(1)设定惯性权重w的取值范围[wmin,wmax]。在迭代的第一阶段,采用大惯性权重wmax使粒子能够以较大概率摆脱局部极值;
(2)计算每一步的惯性权重值。其公式如下:
(5)
式中:iter1,iter2—第一、二阶段的总步数;iter—当前步数。
与此同时,笔者监测此时粒子群体的收敛情况,如判断出粒子早熟,则随机选取部分粒子进行混沌寻优;
(3)采用小惯性权重wmin提升粒子的收敛程度和结果的精确度。
混沌寻优的详细过程如下:
(1)确定适应度不变的最大代数count,在迭代过程中记录粒子群的群体最佳适应度J(gb)连续不变的代数;

ICPSO算法流程如图2所示。

图2 ICPSO算法流程图
1.3 摩擦参数辨识方法
摩擦参数的辨识可以分为静态参数辨识和动态参数辨识两个部分。静态参数辨识需要系统的速度达到稳态,根据依次递增的系统速度及对应的摩擦力矩可以得到Stribeck曲线。
此时,LuGre模型退化为Stribeck模型,即:
(6)
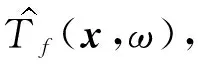
当系统处于低速非稳态时,动态参数成为决定系统摩擦力特性的主导因素[16]。因此,动态参数的辨识需要在系统小位移、低速度的条件下进行。
由于微观下的刚毛变形量无法测得,本文将系统的微小位移s(t)合理近似成刚毛变形量,角速度取转角的差分,此时LuGre模型简化成以下形式:
(7)
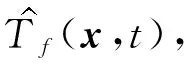
1.4 摩擦参数辨识仿真

据此,在MATLAB/Simulink下搭建的仿真模型如图3所示。
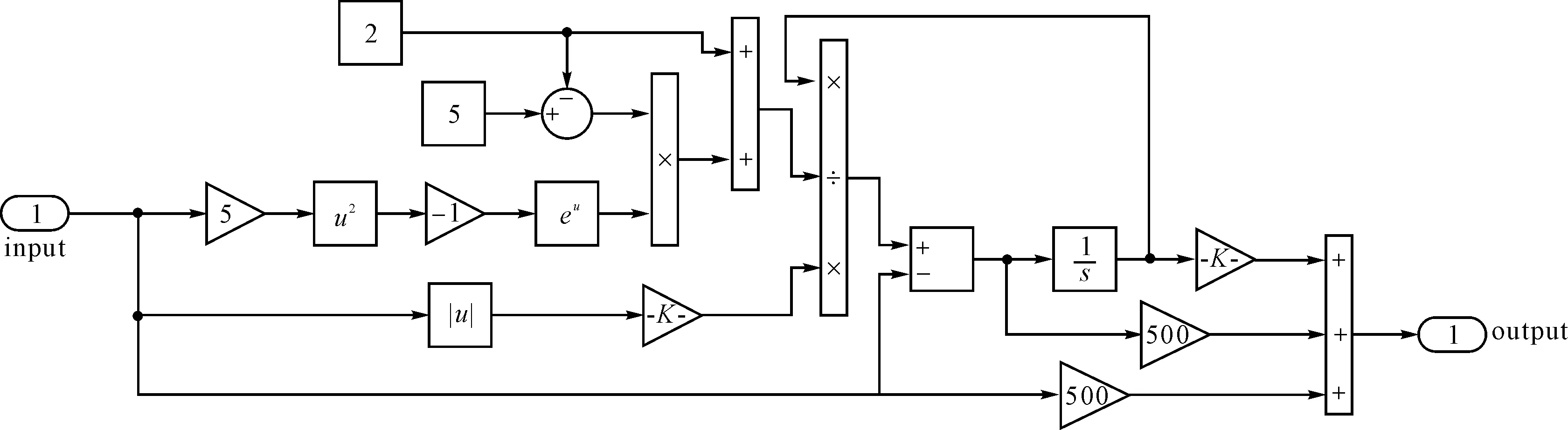
图3 参数辨识仿真模型
该模型以系统角速度为输入,摩擦力矩为输出。在图3所示的仿真模型中,为方便进行后续的参数辨识仿真实验,摩擦参数以常量形式进行了人为设定,具体设定参数如下:Ts=5 N·m,Tc=2 N·m,ωs=0.2 rad·s-1,σ0=50 000 N·m·rad-1,σ1=500 N·m·s·rad-1,σ2=0.5 N·m·s·rad-1。
在MATLAB/Simulink中,笔者对图3所示仿真模型的输入端施加不同的角速度,具体为:从0.02 rad/s开始,以0.02 rad/s为间隔依次递增至2 rad/s。在每一个不同的角速度输入下,让系统仿真计算10 s的时间,使输出摩擦力矩达到稳态,记录不同输入角速度下的稳态摩擦力矩大小。
根据输入角速度与输出摩擦力矩可以绘制Stribeck曲线,如图4所示(负速度部分完全对称,此处略去)。

图4 Stribeck曲线
在静态参数辨识中,将稳态角速度从0.02 rad/s,以0.02 rad/s为间隔依次递增至2 rad/s,并同时测出稳态输出力矩,得到100个原始数据点,然后,先对所得数据的正斜率部分以及负斜率部分进行线性拟合,可以确定出静态参数的估计值,以此为搜索中心可以使粒子群算法的结果更为精确。
在动态参数辨识中,以s(t)=0.1×10-4sin(0.001t)作为系统的角度输入,以s(t)的导数作为系统的角速度输入,持续仿真10 s,将所得结果作为原始数据。
之后,笔者分别采用未优化的普通PSO算法以及ICPSO算法分别进行辨识实验。
实验过程中,统一设定最大迭代次数为300,自我学习因子c1=2,群体学习因子c2=2,粒子群数量为100进行实验。每种算法分别进行独立重复实验100次,取100次实验的平均值作为各自的最终结果。
实验结果如表1所示。

表1 参数辨识仿真实验结果
从表1数据可得:相对于PSO算法,ICPSO算法对于Ts,Tc,ωs,σ0,σ1,σ26个摩擦参数的辨识精度均有所提升。
各项参数绝对误差下降的比例如表2所示。

表2 参数辨识绝对误差下降比例
从表2数据计算可知:与PSO算法相比,利用ICPSO算法进行摩擦参数辨识,可以使绝对误差平均下降42.6%。
2 全闭环控制策略
2.1 反向运动间隙
机械结构之间存在的运动间隙会导致全闭环系统的运动特性变差,其中,最明显的特征就是系统在反向运动时为克服间隙产生的“平顶”现象。
令伺服电机以正弦形式运动,采集电机编码器的位置信息可以得到半闭环的位移图像,采集光栅尺读取到的位移信息可得到全闭环的位移图像,将两者同时做出,得到双位置环位移图像,如图5所示。

图5 双位置环正弦位移图像
从图5中可以看出:在光栅尺反馈的全闭环位移信息中,每当系统运动方向变化时,都会出现一小段位移不变的折返平顶;
在此期间,虽然电机角度仍在变化,但是光栅尺显示的位置信息始终不变。产生这种现象的原因有两个:(1)光栅尺的精度有限,在折返时由于系统的速率很小,所以会产生短暂的平顶;(2)全闭环系统引入了更多的机械间隙,每当系统运动的方向改变时都需要花费额外的时间度过间隙,从而影响了动态特性。
2.2 全闭环混合控制策略
针对全闭环控制中面临的摩擦与间隙等非线性因素,本文提出一种基于前馈摩擦补偿模块、折返速度补偿模块以及PID控制器的混合控制策略。
其中,折返速度补偿模块的原理如下:在伺服系统运行时,在主机程序中设计一个标志位,记录系统运动的方向;当判断出位置指令会使系统运动的方向发生改变时,为电机目标速度增加一个常量ΔV;与此同时,监测伺服系统中光栅尺的读数情况,如果脉冲数为0,则在下一个控制周期继续增加ΔV,否则,停止间隙速度补偿。
利用该策略可以缩短系统间隙的过渡时间,增强系统位置跟随的动态精度。
全闭环混合控制策略的控制框图如图6所示。
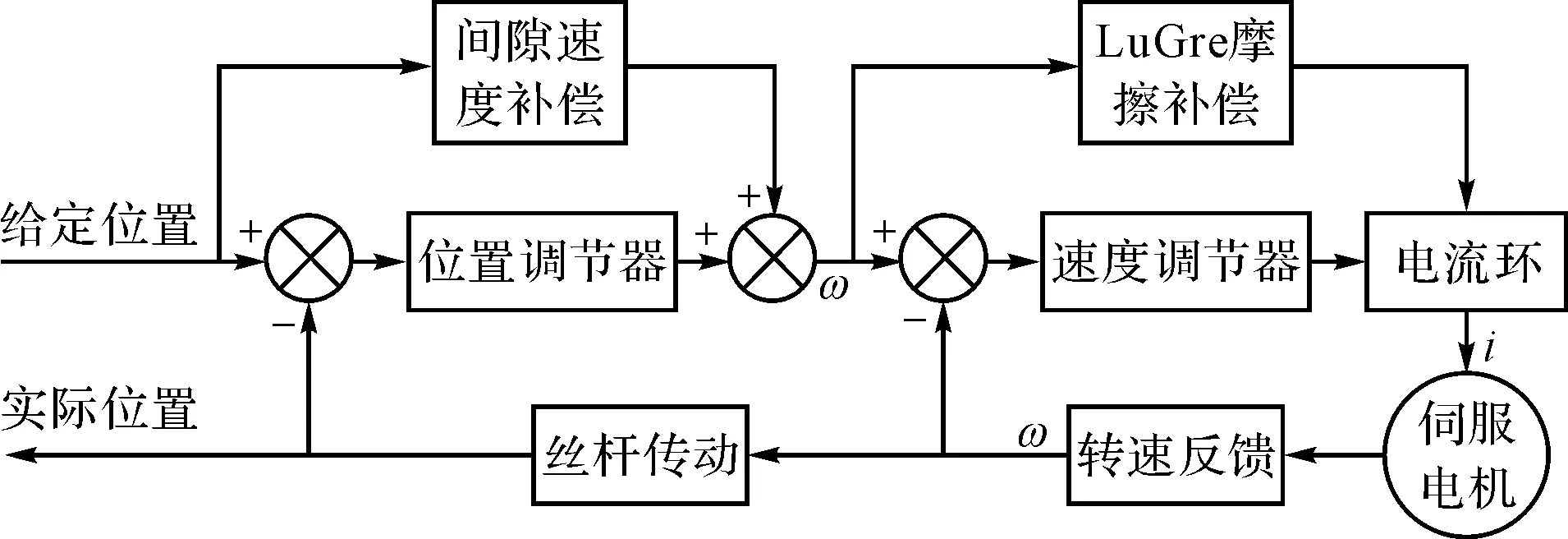
图6 全闭环混合控制策略
3 实验验证
3.1 实验平台
该伺服控制系统基于倍福公司的TwinCAT3平台。控制主站采用Windows10系统计算机,控制从站包含EtherCAT端子模块(EK1100、EL5151)以及copley电机驱动器。
硬件选型:丝杆导轨行程800 mm,丝杆直径16 mm,导程5 mm;直流伺服电机额定电压24 V,空载最高转速2 000 r/min,最大扭矩0.32 N·m,电机前端装有减速器,减速比9 ∶1;相对式光栅尺有效行程920 mm,分辨率5 μm;负载块质量7.5 kg。
该实验采用的控制时钟周期为250 μs,可以满足对系统状态的实时反馈。实验过程中,采用TwinCAT3的Scope View模块实现对于光栅尺位移、伺服电机转速以及目标控制量等实验数据的实时采集。
该实验平台的硬件组成部分如图7所示。

图7 实验平台
3.2 摩擦补偿实验
采用摩擦补偿主要是可以保证电机在负载情况下的转速特性。此处首先进行静态参数的辨识:令电机以ω=0.01+k·0.002 rad/s恒速运转,k=200为采样点数;同时,记录对应摩擦力矩的大小;之后采用ICPSO算法对摩擦参数进行拟合计算,最终获得系统静态参数的辨识结果,如表3所示。

表3 静态参数辨识结果
在动态参数辨识过程中,为了使系统能够以足够小的位移运动,笔者采用电机的转矩控制模式;在获得了预位移量、摩擦力矩值后,通过ICPSO算法拟合参数得到的结果,如表4所示。

表4 动态参数辨识结果
之后,笔者通过辨识所得的摩擦参数,设计摩擦补偿模块。
为验证摩擦补偿的效果,此处令电机跟随ω=3.14sin(0.6πt) rad/s的速度曲线,分别在施加与不施加摩擦补偿的情况下运动,得到的未摩擦补偿的速度跟随结果,如图8所示。

图8 未摩擦补偿的速度跟随
摩擦补偿后的速度跟随结果如图9所示。

图9 摩擦补偿后的速度跟随
从图(8,9)中可以看出:在摩擦补偿之前,电机的速度跟随存在明显的低速死区现象存在;在摩擦补偿之后,这种现象得到明显改善。
摩擦补偿前,电机的速度跟随误差情况如图10所示。

图10 补偿前速度跟随误差
摩擦补偿后,电机的速度跟随误差情况如图11所示。

图11 补偿后速度跟随误差
根据图(10,11),并经计算可得,摩擦补偿前伺服系统的速度跟随的最大误差为0.476 9 rad/s,平均误差为1.2×10-2rad/s;补偿后最大误差为0.235 9 rad/s,平均误差为1.9×10-3rad/s。由此可见,补偿后伺服系统速度跟随的最大误差降低了50.53%,平均误差降低了84.17%。
3.3 位置跟随实验
此处,令系统跟随以x=0.8sin(0.4πt) mm的位移规律运动,分别在普通PID控制器与混合控制策略下运动,得到的PID控制位移跟随曲线如图12所示。
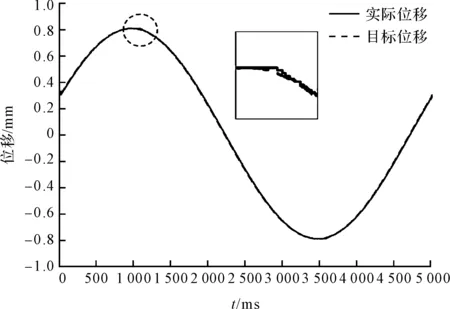
图12 PID控制位移跟随曲线
得到的混合策略位移跟随曲线如图13所示。
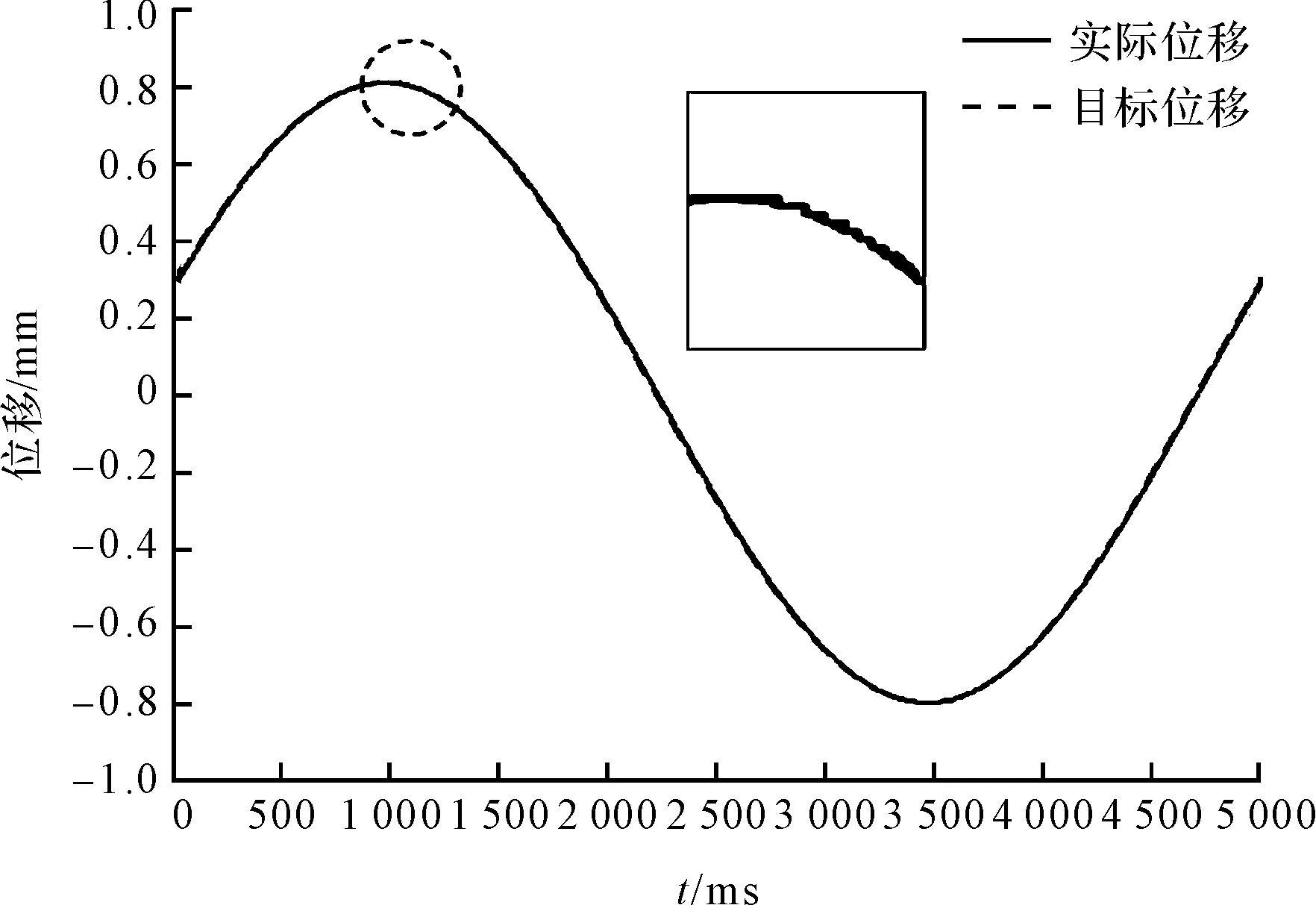
图13 混合策略位移跟随曲线
从图(12,13)中的细节可以看出:采用混合策略的全闭环伺服系统可以有效降低折返处的位置误差。
采用PID控制的位置跟踪误差如图14所示。

图14 PID控制位置误差
采用混合控制策略的位置跟踪误差如图15所示。
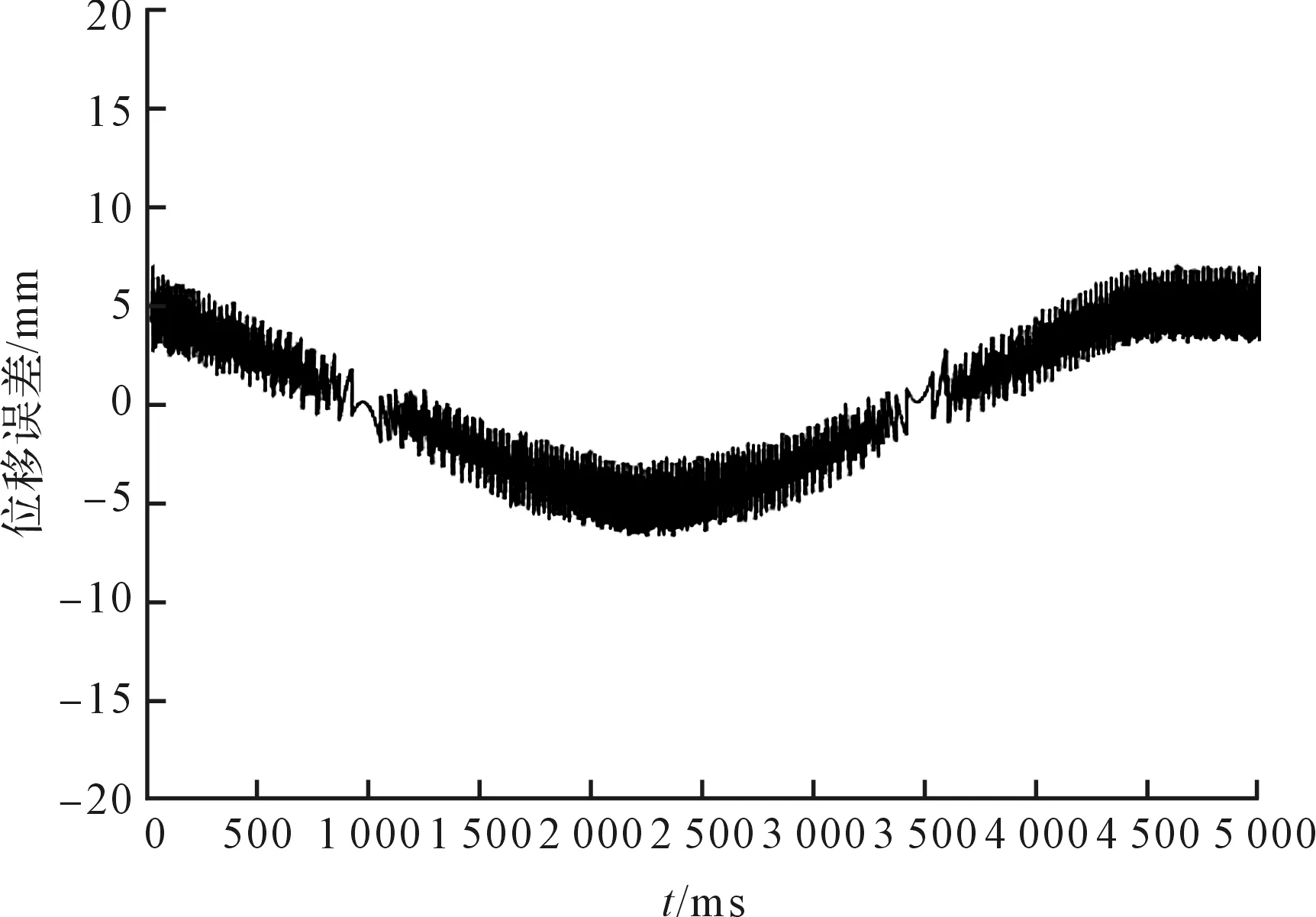
图15 混合控制位置误差
根据图(14,15),并经计算可得,采用PID控制的位置跟踪误差最大为14.91 μm,平均跟踪误差为6.81 μm;而采用混合控制策略的位置跟踪最大误差为11.77 μm,平均跟踪误差为5.11 μm,并且没有误差突变现象产生。
4 结束语
本文提出了一种改进的混沌粒子群算法,提升了摩擦参数辨识精度;针对滚珠丝杆全闭环伺服系统,设计了一种混合控制策略,提升了系统的动态响应。通过仿真与实验的研究得出以下结论:
(1)在仿真实验条件下,改进的混沌粒子群算法相比于常规的粒子群算法精度更高,使参数辨识的绝对误差平均下降42.6%;
(2)针对本文搭建的滚珠丝杆全闭环伺服系统,采用改进的混沌粒子群算法进行参数辨识的摩擦补偿可以有效消除全闭环系统的低速死区,使系统的速度跟随精度提升50%以上;
(3)基于前馈摩擦补偿和反向速度补偿的混合控制策略,可以有效降低系统由于反向运动造成的位置跟随误差。
在后续的研究工作中,笔者将针对不同工况下的有间隙的位置伺服系统,采用混合控制策略展开实验探究,并对不同系统的参数取值方法进行深入研究。
