面向齿轮传动系统协同设计的任务规划方法研究*
2021-09-27刘文林马雅丽李胜甲闫立山
刘文林,马雅丽,李胜甲,闫立山
(大连理工大学 机械工程学院,辽宁 大连 116024)
0 引 言
由于具有效率高、结构紧凑、工作可靠、寿命长等一系列优点,齿轮传动系统被广泛地应用于航空、航天、车辆、船舶等机械领域。齿轮传动系统的工作性能对整个机械系统的影响巨大。
随着数字化、智能化技术的快速发展,客户需求呈现多样性、灵活性、定制化的特点。为快速响应客户需求,缩短产品研发周期,协同设计模式[1]得到了广泛应用。
齿轮传动系统协同设计是指由多个设计人员面向齿轮、轴、箱体等不同设计对象,从构型、结构、性能等方面通过数据交互与特定的协同机制完成齿轮传动系统的设计。齿轮传动系统协同设计的各个任务间存在复杂的交互耦合关系,造成设计流程混乱无序,存在迭代返工等风险。为了有效地组织协同设计,缩短设计流程的执行周期,必须对各环节中的任务进行合理的规划。所谓任务规划,是以减少任务的迭代次数和时间为目的,对协同设计中的各任务进行分解与重组,确定最优的任务执行次序。
目前,国内外有关任务规划的研究主要集中在任务分解、任务流程建模及耦合任务的识别与规划等方面。
杨育等人[2]针对产品协同设计任务分解及分配的复杂性问题,考虑设计任务间的依赖关系,提出了基于功能-结构-任务映射的层次任务分解模型,并对协同设计中的资源分配问题进行了研究。包北方等人[3]针对产品协同设计过程中任务分解缺乏定量分析的问题,提出了一种综合定量分析任务粒度、任务耦合度、任务均衡度的任务分解模型。GOLPAYEGANI S H等人[4]以设计任务的特征属性为输入,通过模块化神经网络模型实现了项目、功能、关系3个层面的任务分解。焦合军等人[5]从并发性、伸缩性、协同性、动态性和组合性5个方面分析产品协同设计过程的特点,提出了基于混合Petri网三维分布的工作流模型,并从任务分解及冲突等方面对其进行了验证。MEIER C等人[6]提出了基于信息流的设计任务规划模型,采用设计结构矩阵(design structure matrix,DSM)来表示设计任务,并将改进的遗传算法应用于信息流模型,从而找到了设计任务的最优规划结果。温跃杰等人[7]将DSM技术应用于航天器研制的设计流程与数据建模,清晰地描述了航天器各设计活动间的数据耦合关系,实现了各个分系统、各个模块、各个学科的数据一致与动态关联更新。郭凯等人[8]通过对设计过程所转化的有向图及其转置图使用深度优先搜索算法,找出了有向图中的强连通分支,实现了对设计任务中耦合任务集的识别。LIN Jun等人[9]基于模糊集理论,建立了DSM中相关任务排序的数学模型,解决了任务不确定性依赖关系的问题。李潇波等人[10]通过DSM优化算法实现了对耦合设计任务的顺序规划,并提出了DSM复杂度的计算方法。王志亮等人[11]针对时间是市场竞争的核心这一特征,提出了基于任务期限的耦合设计任务规划模型,实现了对复杂耦合系统设计任务的管理与协调。田启华等人[12]针对大容量耦合设计任务,提出了基于聚类分析的任务规划新方法,有效缩短了设计任务的执行周期。
以上文献通过对设计任务的分析,用不同的方法提出了任务分解、建模、规划的解决方案,但大都是对耦合任务集本身进行定性的分析,即大部分研究集中在局部规划上,缺少从综合系统的角度并可以进行定量计算的任务规划方案。另一方面,面向齿轮传动系统协同设计任务规划的相关研究也较少。
因此,为解决齿轮传动系统协同设计任务间耦合关系复杂,迭代返工次数多,设计流程混乱的问题,本文提出基于模糊设计结构矩阵(FDSM)的全局-局部两级任务规划方法,并对耦合设计任务间的数据交互程度进行定量计算,可以快速获得最佳的设计任务规划方案;并以齿轮传动系统协同设计为例,对所提的任务规划方法进行验证,获得相应设计任务的最优执行序列。
1 协同设计任务分解与建模
1.1 任务分解
任务分解是齿轮传动系统协同设计的基本问题。任务分解的目的是将一个任务分解成多个子任务,以便多个设计人员协同完成。
复杂产品协同设计可以按照产品-部件-零件的层次关系进行分解,与其对应的任务层次结构为总任务-子任务-元任务,其层次结构如图1所示。

图1 任务分解层次结构图
设计任务不仅包括设计对象、内容,也包括任务所在层次、输入与输出数据以及执行时间等。
为清晰、准确地表示设计任务,本文用集合的方式描述设计任务。
定义1:设计任务。
其形式化描述为Ti={TNi,TLi,TIi,TOi,TRi,TTi,TCi}。
各元素依次表示设计任务的名称、所属层次、输入数据集合、输出数据集合、关系集合、执行时间、成本。
设计任务间通过输入输出数据形成约束关系,从数据流的角度可以分为并行独立型、串行依赖型、交互耦合型3种,即:
(1)并行独立型。设计任务T1,T2不存在数据交互,时序上可以并行执行;
(2)串行依赖型。设计任务T2需要任务T1的输出数据作为输入才可以执行,时序上有先后;
(3)交互耦合型。设计任务T1,T2存在双向的数据交互,需要经多次迭代才能完成任务,时序上有重叠。
分解后设计任务间以层次关系及约束关系为导向进行数据传递,相应的设计任务完成数据的接收、处理与输出。
1.2 基于FDSM的设计任务建模
为了描述和组织设计任务,EPPINGER S D等[13]提出了表达多个设计任务之间关系的设计结构矩阵,其定义为:设有设计任务T={T1,T2,…,Tn}(其中:n—设计任务数量),则其设计结构矩阵为一个n阶矩阵T(其中:矩阵元素tij=1,表示任务Tj对任务Ti有数据输入;tij=0,表示任务Tj对任务Ti无数据输入)。
设计结构矩阵如图2所示。
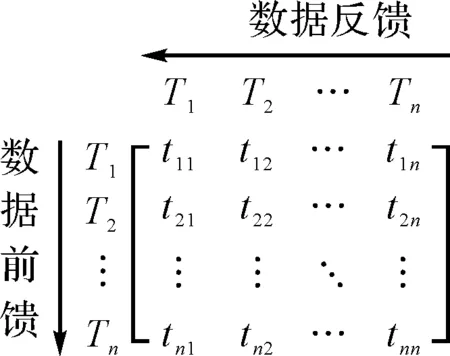
图2 设计结构矩阵
传统的DSM中以布尔值0,1来描述设计任务间是否有约束关系,只能进行定性的分析。
为量化设计任务间的耦合程度,在此处笔者引入任务模糊耦合度的概念。
定义2:任务模糊耦合度。
任务模糊耦合度是用来量化两个任务间输入输出数据交互程度的模糊数。
其计算方法如下:
(1)
(2)
式中:card(TIi)—设计任务Ti输入数据的数量;card(TOj)—设计任务Tj输出数据的数量;card(TOj∩TIi)—设计任务Tj输出数据与Ti输入数据间有映射关系的数据数量;card(TIi∩TOj)—设计任务Ti输入数据与Tj输出数据间有映射关系的数据数量。
为方便计算,本文将区间[0,1]离散化为7等份,将式(1,2)计算得到的耦合度近似等效为模糊数0,0.1,0.3,0.5,0.7,0.9,1,依次表示耦合程度的极低、非常低、低、一般、高、非常高和极高;并把基于任务模糊耦合度建立的DSM称为模糊设计结构矩阵(FDSM)。
设计任务间3种约束关系的图形表达及FDSM表达如表1所示。

表1 3种设计任务间约束关系及其FDSM表示
表3中,通过模糊设计结构矩阵对设计任务建模,简明地表达了设计任务之间的约束关系及耦合程度,为协同设计任务规划提供了模型基础。
2 协同设计任务规划
协同设计任务规划旨在降低任务间的耦合程度,减少设计过程中的迭代次数,优化设计任务执行序列,以缩短产品的开发时间。
本文提出的基于FDSM的全局-局部两级任务规划方法,如图3所示。

图3 基于FDSM的全局-局部两级任务规划方法
2.1 全局规划
全局规划通过对FDSM实施行列变换,识别耦合设计任务并进行归一化处理,使其成为下三角矩阵,实现设计任务迭代数量的减少与影响范围的缩小。
全局规划算法步骤如下:
步骤1:分离独立型设计任务(表现为设计任务的输入数据或输出数据与其他任务无关,即FDSM中的某一行或某一列为零)。
(1)计算FDSM中设计任务的行和、列和。

M,N={1,2,…,n}
r=1
s=1
(2)寻找行和为0对应的设计任务并前置、列和为0对应的设计任务并后置。即求:k,m∈N,使得Rk=0,Cm=0。
设:rank(k)=r
r=r+1
N=N-k
rank(m)=s
s=s-1
M=M-s
如果M,N=Ø,则停止循环,计算完成。
步骤2:识别耦合任务。
(1)构造模糊可达矩阵P。
P=(In+T)n,In—n阶单位矩阵。
(2)构造强连通矩阵Q。
Q=P∩PT=(q1,q2,q3,…,qn)T,qi—n维行向量。

(3)将识别的耦合设计任务归一,即将耦合任务集{Tj1,Tj2,Tj3…,Tjv}整合为一个子任务TC。
步骤3:对非耦合的设计任务进行规划。
(1)构造缩减矩阵。
对耦合任务集进行归一化处理后得到的FDSM称为缩减矩阵。
(2)非耦合设计任务的规划。
E0=(1,1,…,1)T
其中,l≥1。
对于Ti∈T,Ti是T的第l个设计任务的充要条件是oi=1。
2.2 局部规划
局部规划是以全局规划后的耦合任务集为对象,基于任务模糊耦合度,定量计算设计任务间的数据交互程度,找出其中耦合程度最小的设计任务,并以此对耦合任务集进行解耦与规划,最终确定耦合任务集内部的设计任务执行次序。
局部规划算法步骤如下:
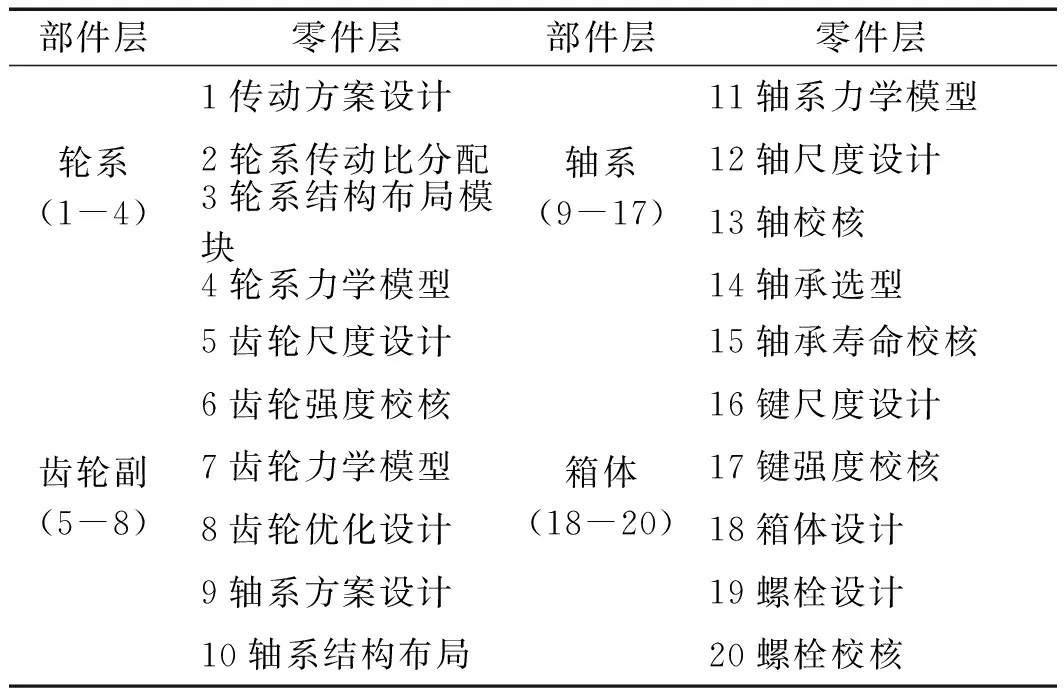
步骤1:基于模糊耦合度,对设计任务数据输入量DIi、数据输出量DOi进行计算。
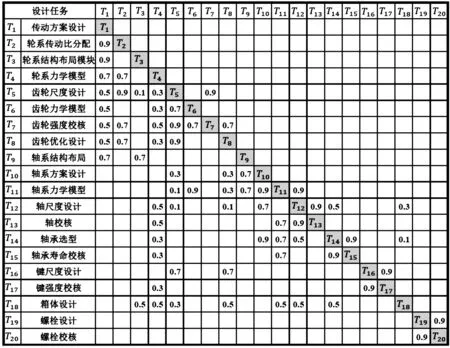
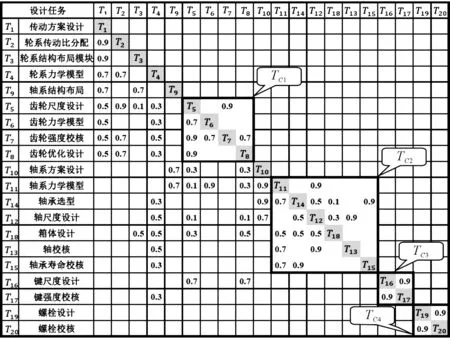
对于设计任务Ti,若与越下游的设计任务Tj有耦合关系,其迭代影响范围越大。本文以设计任务在FDSM中的相对距离,即从tij到tii的距离w,来表征不同设计任务迭代影响范围的大小。对于对角线上方的元素tij(i 可得设计任务数据输入量与数据输出量的计算表达式为: (3) (4) 步骤2:耦合设计任务集的规划: Gi=DIi/DOi (5) DIi与DOi之比为耦合设计任务的排序系数,Gi越小,表明该设计任务相对所需的输入数据量越小,输出数据量越大,即该设计任务在耦合集内应前置;反之亦然。 为验算规划前后矩阵的复杂程度,判断规划过程是否合理,文献[15]提出了G-value的概念,对矩阵的复杂程度进行计算,其表达式为: (6) 可见,通过对分解后的设计任务进行全局规划和局部规划,实现了对耦合任务集的识别、解耦及非耦合设计任务的规划,减少了设计的迭代次数,优化了设计流程。 齿轮传动系统是一种典型的复杂产品,其结构复杂,设计过程涉及多对象、多内容的耦合,按照传统设计方法进行设计,不仅存在周期长、成本高的问题,而且难以保证设计性能最佳。 此处,笔者以齿轮传动系统协同设计为例,对基于FDSM的全局-局部两级任务规划方法的可行性和有效性进行验证。 根据齿轮传动系统设计生产实际,并结合有关的参考资料,笔者将齿轮传动系统协同设计任务分解为轮系、齿轮副、轴系、箱体4个部件层子任务,下分20个零件层元任务,如表2所示。 表2 齿轮传动系统设计任务 然后通过分析各设计任务间数据交互情况,计算各设计任务间的模糊耦合度。 这里以传动方案设计与传动比分配两个设计任务间的模糊耦合度计算为例进行说明。 通过调研分析得到TI1={输出转速,总传动比,输入、输出轴的轴线关系},TO1={传动级数,第1级传动类型,第2级传动类型,第3级传动类型,第4级传动类型,第5级传动类型};TI2={总传动比,传动级数,第1级传动类型,第2级传动类型,第3级传动类型,第4级传动类型,第5级传动类型,传动比分配系数},TO2={第1级传动比,第2级传动比,第3级传动比,第4级传动比,第5级传动比}。 根据式(1,2)可以计算得到t12=0,t21=0.85≈0.9。其他设计任务间模糊耦合度的计算这里不再赘述。 最终构建的FDSM如图4所示。 图4 齿轮传动系统协同设计任务初始FDSM 3.2.1 全局规划 具体的步骤如下: (1)分离独立型设计任务; (2)识别耦合任务; 根据2.1节中提供的方法,经计算可得到模糊强连接矩阵Q及4个耦合任务集TC1~TC4,如图5所示。 图5 强连接矩阵Q (3)非耦合设计任务规划。 将耦合任务集归一化后,得到缩减矩阵与排序矩阵,如图6所示。 (a)缩减矩阵P′ 3.2.2 局部规划 此处以图4中的耦合任务集TC2为例进行说明。根据FDSM中设计任务的模糊耦合度,结合2.2节权重确定规则,计算TC2中各设计任务的数据输入量、数据输出量及其比值,结果如表3所示。 表3 齿轮传动系统设计任务 根据Gi值的大小排序,可得到耦合设计任务集TC2中各任务的执行顺序为:T11→T14→T12→T18→T13→T15。 根据式(6)进行计算,可得到规划前后FDSM的复杂程度G-value分别为318.847 3、206.203 1,复杂程度降低了35.32%;且规划后设计任务执行次序得到优化。该结果验证了全局-局部两级任务规划方法的合理性。 重组后的FDSM如图7所示。 图7 规划后FDSM 本文面向齿轮传动系统协同设计中的任务规划问题进行了研究,为合理配置设计任务、缩短设计周期,提高齿轮传动系统协同设计效率提供了一种新方法。 本文的主要结论(贡献)如下: (1)基于任务层次分解结构将设计任务划分为相应的任务子集,通过任务模糊耦合度量化任务间的数据交互程度,再结合DSM实现了设计任务建模,为协同设计任务规划提供了模型基础; (2)提出了基于FDSM的全局-局部两级任务规划方法,并给出了相应的算法步骤,实现了对耦合设计任务的识别与解耦、非耦合设计任务的规划; (3)以齿轮传动系统协同设计为例,阐述了整个规划过程,规划后FDSM的复杂程度降低了35.32%,设计流程得到了优化,验证了所提方法的可行性与有效性。 在接下来的研究中,笔者将对任务规划后的任务分配问题进行研究,主要考虑分配过程中时间、成本、复杂度等资源的协同,最终得到任务的分配方案。
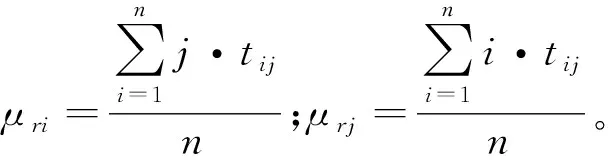
3 齿轮传动系统协同设计任务规划
3.1 任务分解与建模
3.2 任务规划




4 结束语
