风电偏变驱动器设计中的齿轮轴轴承校核问题研究*

2021-09-27徐雁波郭媛媛贾松阳

机电工程 2021年9期

徐雁波,郭媛媛,贾松阳

(1.商丘工学院机械工程学院,河南商丘 476000;2.洛阳LYC轴承有限公司,河南洛阳 471039;3.航空精密轴承国家重点实验室,河南洛阳 471039)

0 引言

随着风能产业的迅速发展,风机设备需求的日益加大,对风机设备的要求也变得更高[1-5]。其中,风机设备中偏航和变桨驱动器的作用是根据风向调整叶片角度。驱动器内部齿轮轴上的2个圆锥滚子轴承一般为标准尺寸单列圆锥滚子轴承,通常为30、32、33系列。驱动器的工况特点是转速慢,但传动比大。两者转速通常小于2 r/min,且长时间工作于1 r/min以下。偏航驱动器与偏航回转支承的齿轮传动比通常在1∶1 000左右,因此,驱动器齿轮传递到轴承的载荷较大。

标准尺寸轴承已是成熟的基础件产品,其在包括风机在内的各种工程领域得到了广泛应用。而驱动器的作用是根据风向调整叶片角度,其长时间处于不工作或转速极低的工况。因此,在风机整机寿命内,设计合理、安装维护得当的驱动器轴承一般不会出现寿命提前到期的情况。因此,在风机的设计阶段,往往不会对标准轴承进行重新开发,而是选择合适的轴承。轴承的校核就十分重要。

文献[6]提供了一种针对驱动器轴承的简支梁校核计算方法,但在关于轴向力的计算方面,其理论推导部分不完善。因为简支梁算法相对较为简单,所以其在工程上得到了广泛应用;但是否适用于有严格要求的驱动器轴承校核尚有待讨论。

对此,基于工程实际案例,笔者利用Romax仿真软件,对驱动器轴承的简支梁和有限元计算结果进行对比;并在此基础上,基于有限元法补充分析轴承预紧量对驱动器轴承的影响,为风机领域驱动器设计提供参考。

1 强制性要求

偏航驱动器是风机偏航控制系统的机械部件之一,其作用是通过驱动机舱底部的偏航回转支承而使风轮对准风向。

变桨驱动器是风机变桨控制系统的机械部件之一,其作用是通过驱动叶片变桨回转支承而调整叶片角度,以使其能充分利用风力。

风机的偏航与变桨驱动器如图1所示。

(a)偏航驱动器

图1中,通常情况下驱动器采用多台布置,以使其得到对称的驱动扭矩[7,8]。偏航和变桨驱动器结构类似,一般都由齿轮、齿轮轴、两个不同尺寸的圆锥滚子轴承组成。其中,电机侧轴承尺寸较小,而齿轮侧轴承尺寸较大。

在德国劳氏船级社认证体系GL2010中,对风机的施工、设备、维护等进行了详细的规定,这也是目前我国风机领域主要应用的体系标准[9];在进行轴承校核时也应遵循其要求。通常,对于驱动器轴承的型号、安装布局、工况等参数由驱动器制造单位提供。因该类轴承是尺寸不大的标准单列圆锥滚子轴承,材料为钢GCr15或GCr15SiMn,制造过程符合要求。

在以上各项已知的情况下,关于驱动器轴承的强制性规定如表1所示。

从表1中可以看到:驱动器轴承的性能要求必须满足静态安全系数So≥1.1,以及ISO281寿命不低于1.3×105h(约15年)。

表1 关于驱动器轴承的强制性规定

2 简支梁校核算法

2.1 轴承载荷计算

首先,驱动器轴上的载荷来自直齿轮,齿轮力如图2所示。

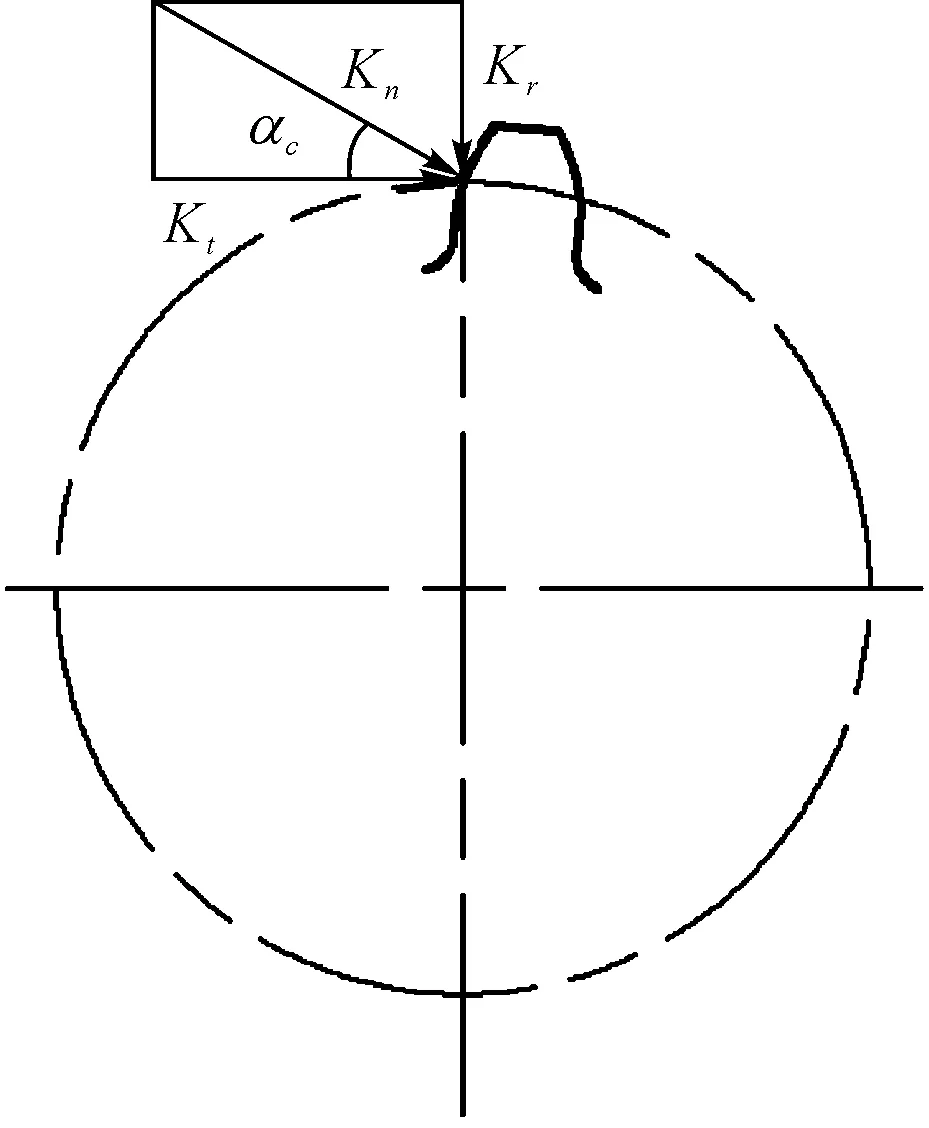
图2 齿轮力

沿啮合线作用在齿面上的法向载荷Kn垂直于齿面,Kr与Kt为其径向和水平分力,无轴向力,其计算方程[10]为:

(1)

式中:M—齿轮扭矩,kNm;Kn—齿轮齿面上的法向载荷,kN;Kr—齿轮法向载荷的径向分力,kN;Kt—齿轮法向载荷的水平分力,kN;m—齿轮模数;z—齿轮齿数;αc—齿轮压力角,°。

根据驱动器布置方式,笔者绘制简支梁算法简图,轴承载荷计算简图如图3所示。

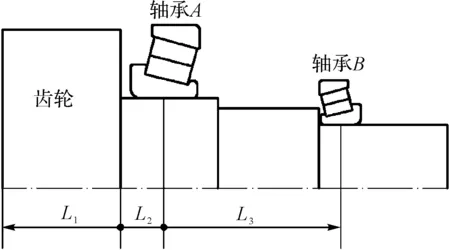
图3 轴承载荷计算简图

平衡方程组为:

(2)

式(2)中,下标A、B分别指轴承A和轴承B(下同)。

其中:

qL1=Kn

(3)

式中:q—单位载荷,kN/mm;L1,L2,L3—间距,mm;Fr—轴承的径向力,kN;Fa—轴承的轴向力,kN。

由此可得:

(4)

需要注意的是,在计算间距时,轴承的节点应是轴承内圈的宽度中心(非轴承总宽度的中心)。

由于直齿轮不产生轴向力,圆锥滚子轴承的轴向力来自于自身派生,即:

如果：

(5)

如果：

(6)

其中:

Y=0.4cotα

(7)

式中:X,Y—轴承的动载荷系数,由GB/T 6391查询;Pr—当量动载荷,kN;α—轴承接触角,(°)。

2.2 轴承校核计算

轴承校核主要是计算出静载安全系数So和给出轴承寿命。

2.2.1 静载安全系数So

静载安全系数So表达式为：

(8)

式中:Po—当量静载荷,kN;Co—轴承额定静载荷,kN。

其中,P0取下列两个方程的较大者,即:

Po=XoFr+YoFa

(9)

Po=Fr

(10)

式中:X0,Y0—轴承的静载荷系数,由GB/T 4662查询得到。

静载安全系数的计算是基于齿轮极限扭矩的。

2.2.2 轴承ISO281寿命

在GB/T 6391中,详细规定了ISO281寿命的计算方法。其中,向心滚子轴承基于转数的计算方程为:

(11)

其中:

Pr=XFr+YFa

(12)

式中:Cr—轴承额定动载荷,kN;L10—ISO281轴承寿命,百万转。

转化为基于小时的寿命计算方程为:

(13)

式中:L10h—ISO281轴承寿命,h;n—轴承转速,r/min。

轴承寿命的计算是基于齿轮额定扭矩的。

3 有限元仿真模型

在传动设计领域,经典Romax Designer软件享有盛誉,目前已成为齿轮传动领域行业的标准工具,尤其在2010年,Romax Wind成为德国劳氏船级社(GL)唯一认证齿轮计算软件[11-17]。Romax软件中包含的高级轴承分析模块在轴承领域也得到了非常广泛的应用[18-22]。

笔者根据驱动器结构建立了Romax有限元仿真模型。驱动器轴承仿真模型如图4所示。

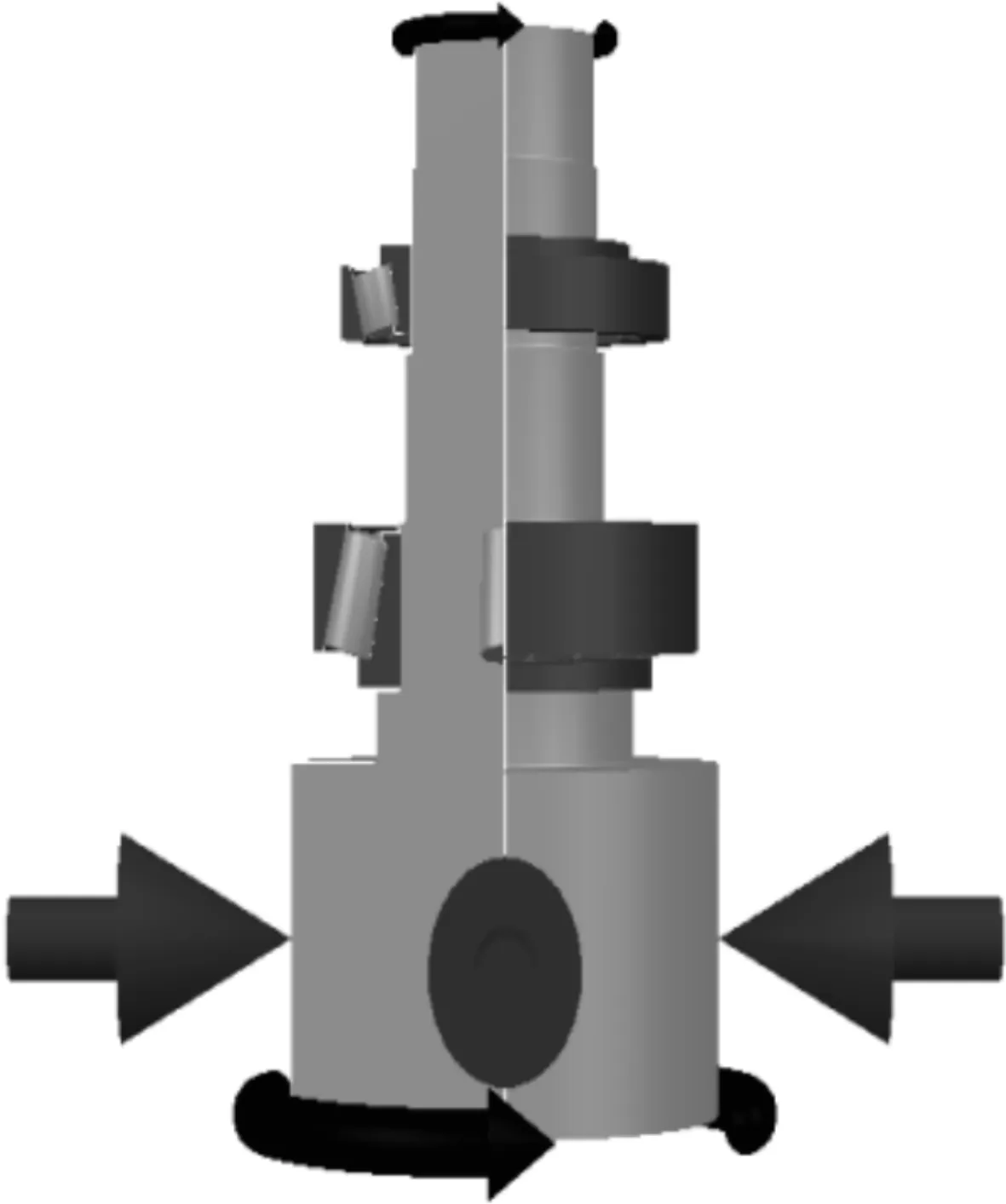
图4 驱动器轴承仿真模型

在轴承配合方面,齿轮侧的轴外径偏差为n6,电机侧的轴外径偏差为m6;座圈内径偏差均为H7。轴承内外径公差按轴承等级查询GB/T 307.1;载荷施加于齿面上,并且沿齿宽均匀分布。

4 实际工程案例分析

为使对比结果具有普遍性,笔者选取了3个实际工程案例,3个工程案例如表2所示(轴承参数来自LYC轴承,详细计算过程省略)。

表2 3个工程案例

静载安全系数S0计算结果如表3所示。

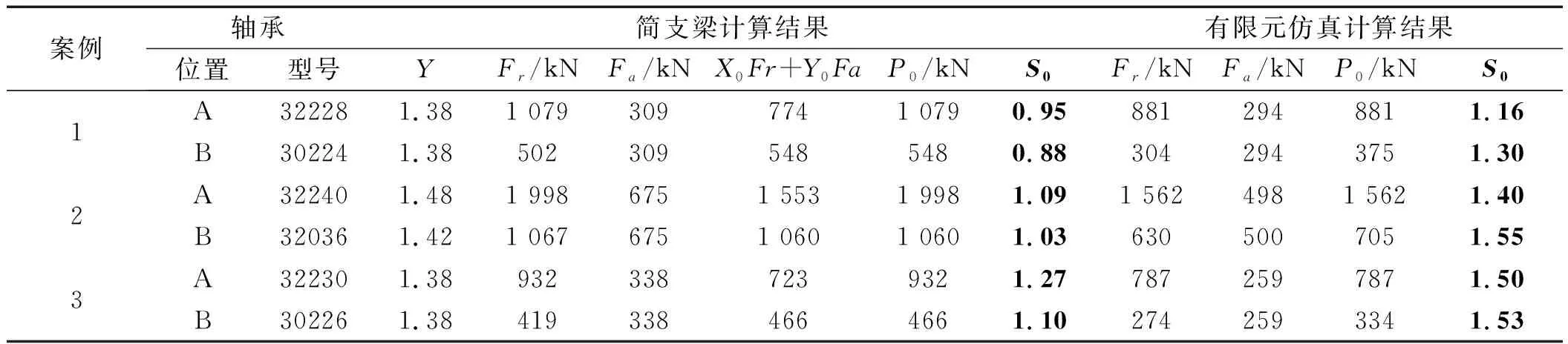
表3 静载安全系数S0计算结果(极限扭矩时)

轴承ISO281寿命L10h计算结果如表4所示。

表4 轴承ISO281寿命L10h计算结果(额定扭矩时)

(续表)

从表2可以看出:有限元仿真的结果均满足体系中规定的S0至少为1.1的要求,但简支梁计算结果中的案例1和2不满足;

从表3可以看出:简支梁计算结果中有一个型号轴承寿命不满足规定的至少1.3×105h的要求,有限元仿真结果均满足要求。

从上述对比中可以看出,在轴承的可靠性和寿命指标上,有限元方法的计算结果均远优于简支梁的计算结果。产生这种情况的主要原因是轴承的径向力和轴向力计算结果差别较大。因为简支梁的刚性轴假设使轴承支撑点获得了更大的载荷,而有限元的柔性轴使轴承支撑点的载荷更小;且轴承寿命对载荷十分敏感,如表3中32036轴承寿命相差超3倍。

从以上对比可以得到的结论是:简支梁算法不适用于风电驱动器轴承的校核计算,工程上应使用有限元方法作为校核方法。