双稳定器预弯曲钻具组合防斜特性动力学评价方法

刘科柔 张辉 王新锐 付豪 刘俞万 路宗羽 石建刚

1.中国石油大学(北京)石油工程学院；2.中国石油新疆油田分公司

0 引言

直井眼的防斜打直一直是钻井领域的难题，目前国内外的防斜打直钻井技术可以分为两大类：被动防斜打直技术和主动防斜打直技术。主动防斜打直技术例如贝克休斯的VertiTrak 系统、斯伦贝谢的PowerV 系统在现场有着非常好的应用效果，但是其使用成本较高，严重限制了其使用范围［1］。被动防斜打直技术又分为静力学和动力学防斜两种，静力学防斜组合通过减少钻具变形，再辅以静力学分析实现防斜目的，此类防斜打直技术在现场应用最为广泛，理论研究也较为成熟，例如满眼钻具组合和钟摆钻具组合；动力学防斜打直技术突破了对底部钻具组合的变形限制，反过来利用其动力学行为来实现防斜，其中预弯曲钻具组合利用预弯曲结构引导钻具组合的变形，从而产生较大的动态降斜力。邓柯［2］在高陡峭地层空气钻井中进行了预弯曲钻具组合的防斜打快试验，结果表明采用预弯曲动力学防斜钻具组合实施空气钻井钻速得到大幅度提高，井斜也能够满足钻井设计要求。预弯曲钻具组合在川西地区的应用中发现，其在中浅部软硬交错地层的防斜和机械钻速提升与进口垂钻系统相当［3］，在超深井的试验中表明其可以在40～100 kN的钻压下有效控制井斜［4］。除此之外，江苏油田［4］、克拉玛依油田［5］、吐哈油田［6］等各油田也均使用预弯曲钻具组合进行了钻进试验，也均取得了良好的增速防斜效果。预弯曲钻具组合的防斜性能评价以静力学合导向力计算为主［7-8］，虽然对于钻具组合在井下运动的动力学模型很多，但是将动力学模拟结果与动态侧向力联系起来的研究并不多，并没有形成直观快速的动力学防斜性能评价方法，近些年来狄勤丰［9-10］将动力学理论应用到预弯曲钟摆钻具组合的防斜特性评价中，建立了动态侧向力计算模型。但是对于双稳定器预弯曲钻具组合，目前还没有一套快速且直观的防斜特性评价方法。

在双稳定器预弯曲钻具组合动力学计算方面，Jansen［11-13］建立了带有质量偏心钻具的动力学计算模型；狄勤丰［14］引入此模型并应用于双稳定器预弯曲钻具的动力学计算。笔者将此动力学模型进一步与预弯曲结构结合并利用仿真得到的涡动轨迹数据建立动态侧向力计算模型，模型结果包括动态侧向力分布时程图及平均动态侧向力等数据，由此可以快速并直观的观察到钻头处动态侧向力的大小及分布情况，进而对双稳定器预弯曲钻具组合的防斜特性进行快速评价。最后对不同井斜角及转速下的防斜特性进行评价，获得这两个参数下的动态侧向力变化规律，这对双稳定器预弯曲钻具组合在现场的实际应用具有重要意义。

1 动态侧向力模型

动态侧向力模型建立在仿真得到的涡动轨迹数据之上，本文使用的动力学模型为Jansen 建立的带有质量偏心的双稳定器钻具动力学模型，首先将预弯曲结构特征以质量偏心的形式代入动力学模型计算，再使用动态侧向力模型计算动态侧向力，由此对钻具防斜特性进行快速直观的评价。

1.1 涡动轨迹计算模型

我们称相邻两稳定器中点处的钻具截面为A 截面，Jansen 对带质量偏心的双稳定器钻具组合A 截面处的受力进行了动力学分析，建立了质量-弹簧模型，若x1和x2分别指向降方位方向和井眼高边方向，A 截面处的钻铤旋转示意图见图1。

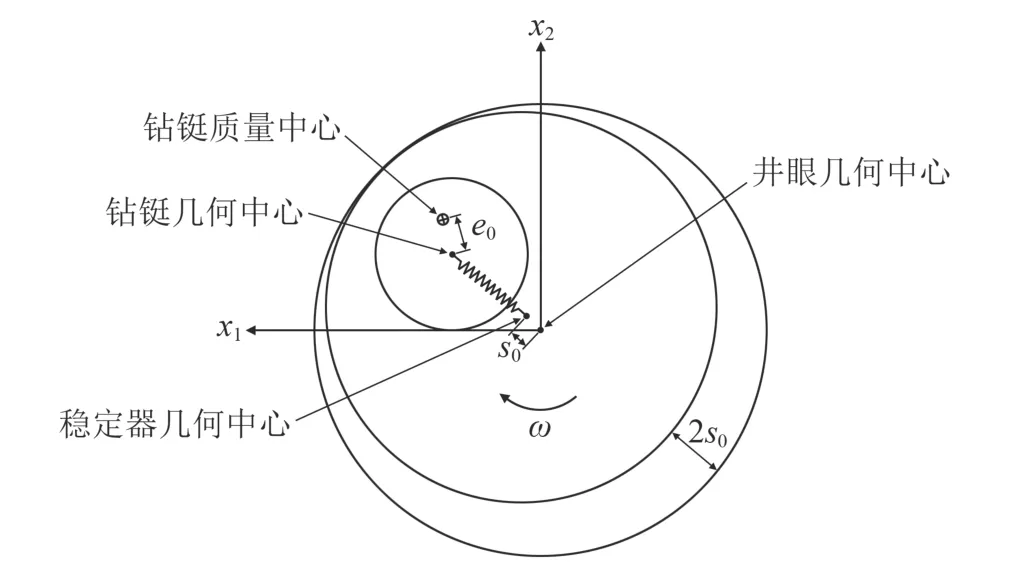
图1 钻铤旋转示意图(A 截面)Fig.1 Diagram of drill collar rotation (Section A-A’)

Jansen 建立的模型中主要考虑了加速度引起的惯性力、弯曲引起的恢复力、钻井液产生的拖拽力及井眼倾斜造成的重力影响，并考虑了稳定器与井眼及钻铤与井壁接触碰撞时产生的恢复力。动力学计算模型最终由方程(1)和(2)表示［11,15］

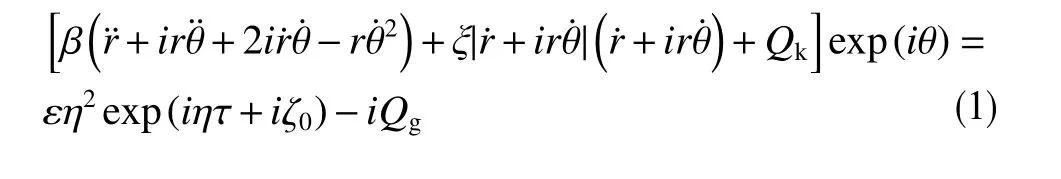
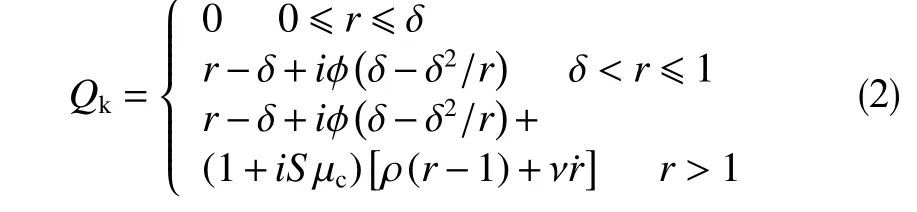
式中，r=q/c0，为钻铤形心距离井眼中心的距离，无量纲；q为钻铤形心偏移井眼中心的距离，m；c0为钻铤间隙，m；θ为钻铤形心以x1为始边顺时针旋转过的角度，rad；β=(mf+m)/m，无量纲；mf和m分别为钻铤和钻井液的等效质量，kg；ξ为钻井液的等效流体黏滞系数，无量纲；δ=s0/c0，无量纲；s0为稳定器间隙，m；ε=e0/c0，无量纲；e0为钻铤的质量偏心距，m；η为转盘转速，无量纲；τ=ωt，无量纲时间；ω为自然角频率，Hz；ζ0为钻铤形心初始相位角，rad；Qg为井眼倾斜造成的重力影响项，无量纲；Qk为稳定器与井眼及钻铤与井壁接触碰撞时产生的恢复力项，无量纲；ϕ为钻头及稳定器处综合摩擦角，rad。

考虑到预弯曲结构在转子动力学中主要对质量偏心距离产生影响，本文将主要在质量偏心方面对预弯曲结构进行考虑。基于先前涡动轨迹模拟规律，可知稳定器在涡动过程中常处于接触井壁的状态，所以稳定器间钻铤可以看作是以双稳定器为简支的转子，因此以双稳定器形心连线为轴线计算质心偏移，以近钻头扶正器三维几何中心为坐标原点，指向井眼方向为z轴，y轴指向井眼高边方向，此时第二扶正器三维几何中心正好位于z轴上，如图2所示。

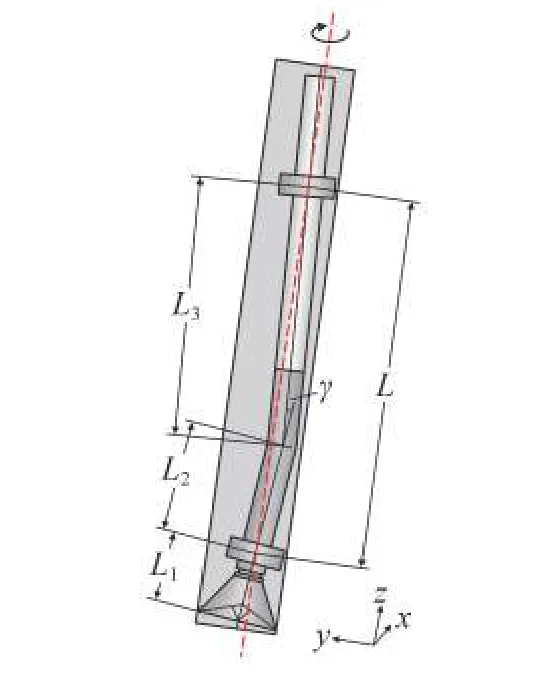
图2 预弯曲钻具组合结构示意图Fig.2 Structural diagram of pre-bending BHA

对于双扶正器预弯曲钻具组合，两扶正器的距离L由式(3)进行计算

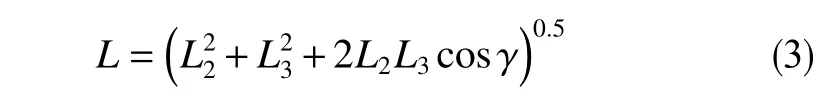
式中，L为近钻头扶正器和上扶正器形心的直线距离；L1为第一跨长度，m；L2为第二跨长度，m；L3为第三跨长度，m；γ为预弯曲结构弯角，rad。

动力学模型没有考虑纵向质心偏移对涡动的影响，所以这里不考虑z轴上质心偏移距离时，根据常规质心和形心的计算公式，质心和形心相对z轴的偏移距离s′和s1的计算公式可由式(4)表示

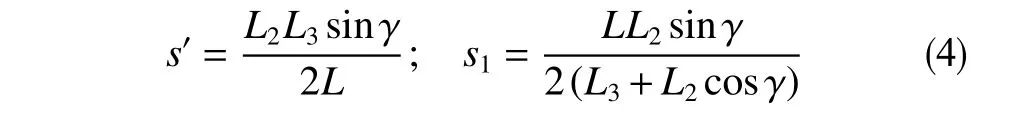
则此时根据偏心距计算公式e0=s1−s′可以得到等效偏心距离e0化简后可由式(5)表示

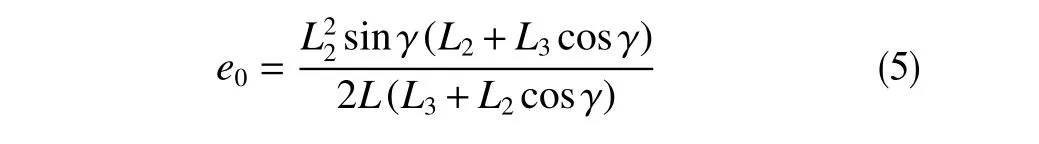
将以上偏心距计算公式带入动力学模型进行仿真可以得到A 截面处形心的涡动轨迹数据。

1.2 动态侧向力计算模型

钻铤形心涡动过程中，由于钻铤的变形弯曲将会在钻铤形心处产生恢复力Fk，在钻头和近钻头稳定器处将因此产生对井壁的冲击力。在不考虑井壁摩擦力的情况下，恢复力方向指向井眼中心；如果考虑井壁摩擦力，则恢复力方向会产生一个ξ1角的偏移，假设此时模型中钻头与近钻头稳定器接触井壁的综合摩擦角为ϕ，则此时的钻铤形心旋转示意图见图3。

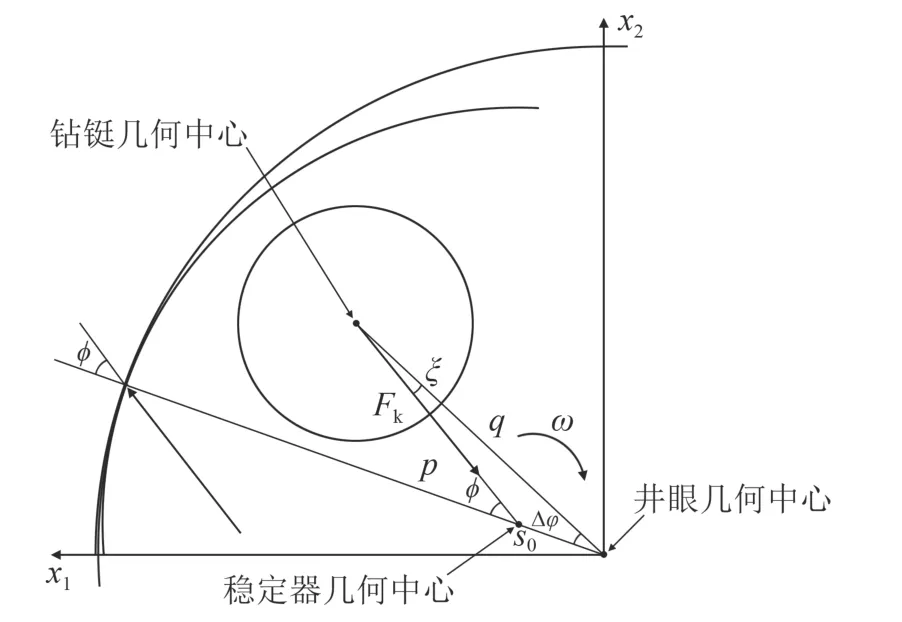
图3 有摩擦力作用时的钻铤形心旋转示意图(A 截面)Fig.3 Schematic diagram of the rotation of the drill collar shape center when there is friction (A section)

由于钻头和近钻头稳定器位置接近，则不考虑钻头与近钻头稳定器间钻具变形时，A 截面处的恢复力可以由A 截面处钻铤形心相对稳定器形心的挠度进行计算，近钻头稳定器接触井壁时Fk的径向、切向分量极坐标表达式［14］可由式(6)表示

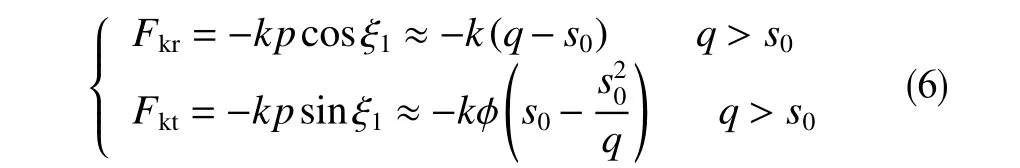
式中，k为等效抗弯刚度，N/m。

假设钻头和近钻头稳定器处的摩擦角均等于Φ，则根据力矩平衡，钻头处和稳定器处由于钻铤涡动产生的对井壁冲击力大小关系可由式(7)表示

由于预弯曲弯角及钻铤的涡动，钻头处将会产生转角，在转角的作用下钻头和近钻头稳定器处产生的力矩将会变化，但这种力矩的变化非常复杂，粗略考虑钻头与近钻头稳定器处产生相同的力矩，则结合式(7)可以得钻头处冲击力大小如式（8）

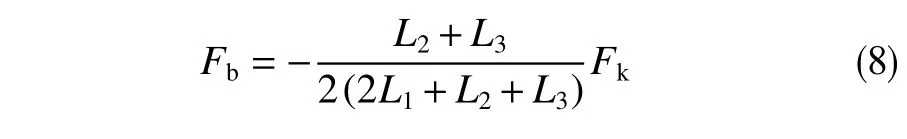
在(x,y,z)坐标系下钻头处冲击力的表达式可以转换为公式(9)

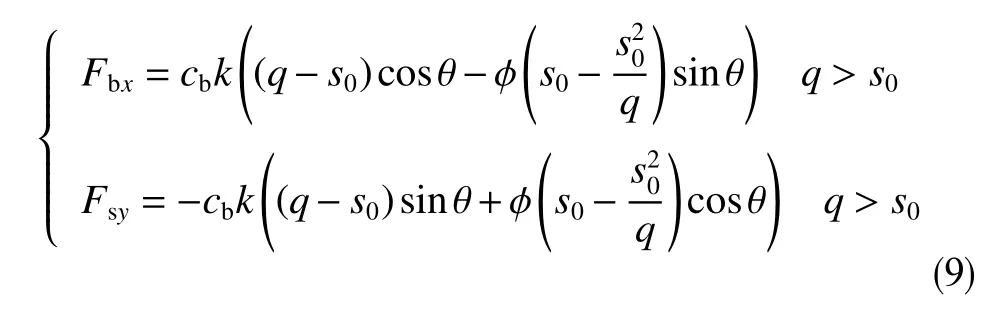
式中，cb为钻头动态侧向力系数，cb=(L2+L3)/(4L1+2L2+2L3)。

将涡动轨迹计算结果带入式(9)可得动态侧向力数据。将动态侧向力随时间的变化绘制于极坐标下可得动态侧向力分布时程图，直观观察到动态侧向力在井壁四周的分布。为进一步定量评价防斜性能，应使用平均动态侧向力对其防斜特征进行评价。形心涡动周期性并不规律，无法以1 个稳定周期下的平均动态侧向力进行定量表述，为了考虑一段时间内的特性，取钻铤涡动基本稳定后一定时间内动态侧向力数据进行平均得到动态侧向力在每秒下的均值，由此到的平均动态侧向力在x,y方向的分力可由式(10)表示

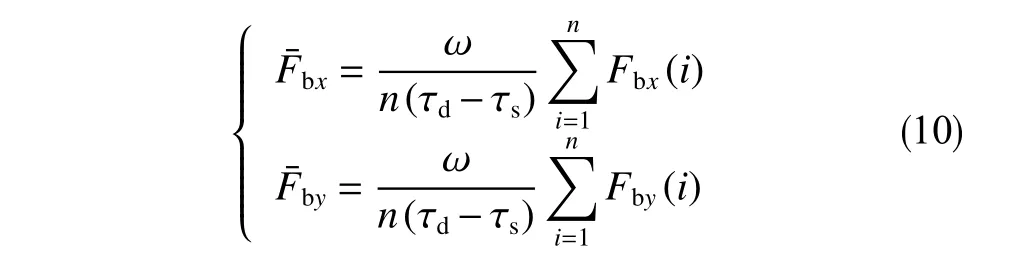
根据x,y方向分力可以由公式(11)和公式(12)表示平均动态侧向力及其方向角(以高边方向为始边，顺时针旋转过的角度)

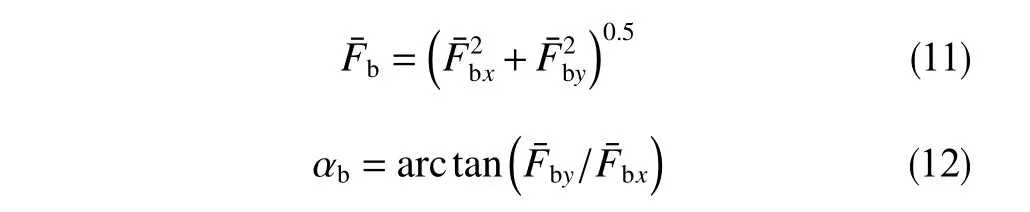
2 BHA 主要参数对防斜特性的影响规律

钻具组合结构参数为：Ø311.2 mm 钻头+Ø308 mm 稳定器+Ø203.2 mm 预弯曲短接(1.25°)+Ø203.2 mm 钻铤+Ø308 mm 稳定器，其中L1=0.7 m，L2=1.2 m，L3=10 m。施工参数为：钻压40 kN，钻井液密度为1.2 g/cm3。

根据本文所述模型，笔者编写了BHA 侧向力仿真软件，由此对上述双稳定器预弯曲钻具组合进行动力学仿真。仿真时钻铤形心的初始参数为：r=0.013；r′=0；θ=0；θ′=0。其他动力学参数为：β=1.32；ξ=0.17；δ=0.86；ε=0.018；η=0.045；ϕ=0.2 rad；μc=0.1，无量纲时间计算范围为τ∈[0,750]，平均动态侧向力取值区间为τ∈[200,750]。

对于井斜角和转速对双稳定器预弯曲钻具组合降斜性能影响规律的研究，有利于预弯曲钻具组合施工参数的优化，对其在现场的使用具有重要意义。

2.1 井斜角对防斜性能的影响规律

转速为60 r/min 时，取1°到6°间六组井斜角对所述钻具组合进行仿真计算，图4 是不同井斜角下A 截面处钻铤形心的涡动轨迹，图5 是不同井斜角下钻头处动态侧向力的分布时程。

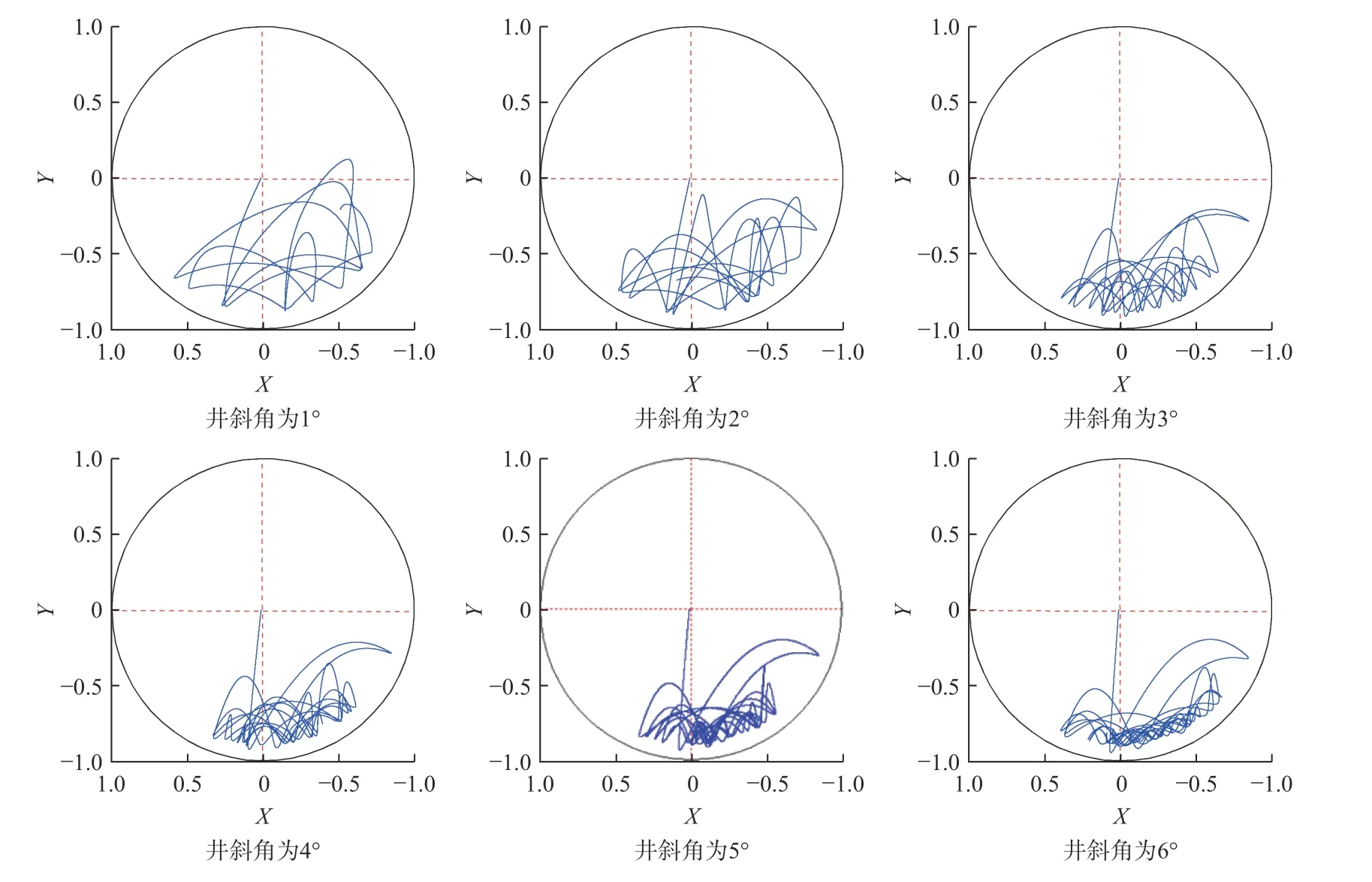
图4 不同井斜角下的钻铤形心涡动轨迹图Fig.4 The whirl trajectory of the geometric section center of a drill collar under different well inclination angles

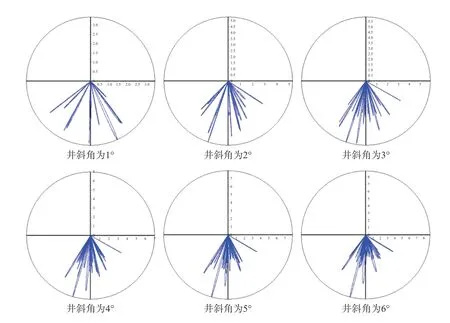
图5 不同井斜角下的动态侧向力分布时程图Fig.5 Time-history chart of dynamic lateral force distribution under different well inclination angles

从图4 和图5 可以看出，钻铤形心涡动轨迹和动态侧向力均偏向下井壁。图6 是平均动态侧向力在x、y方向分力随井斜角的变化曲线。从图6 中可以看出平均动态侧向力始终表现为降斜力。综合来看，随着井斜角增大，降斜力增大，动态侧向力更加集中且冲击次数明显增多，这种趋势非常稳定，能够很好解释预弯曲钻具组合的防斜降斜特性，能够更充分的认识预弯曲钻具组合防斜打直的机理。

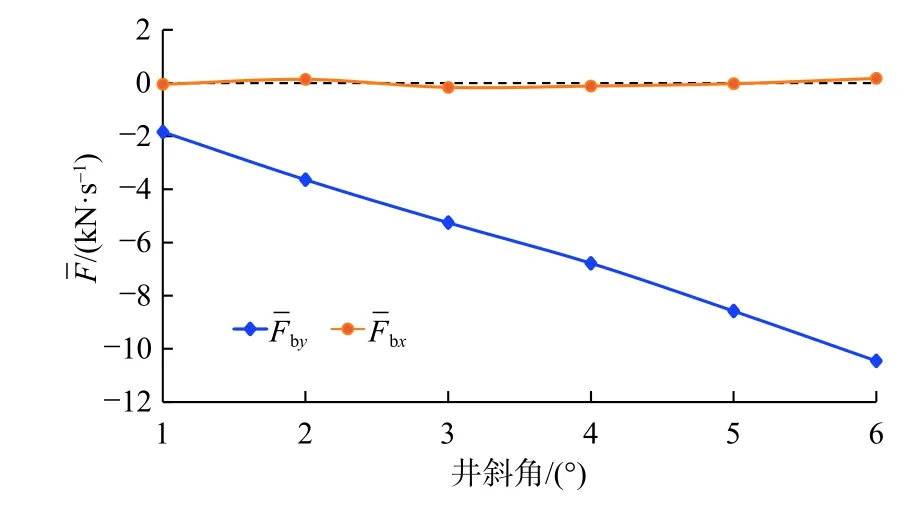
图6 不同井斜角下平均动态侧向力在x、y 方向分力的变化曲线Fig.6 Variation curve of average dynamic lateral force component in X and Y direction under different well inclination angles

2.2 转速对防斜性能的影响

井斜角为3°时，取40 r/min 到190 r/min 间16组转速对所述钻具组合进行仿真计算，图7 是平均动态侧向力在x、y方向分力随转速的变化曲线。从图7 可看出，在90 r/min 前降斜特性表现极稳定；90 r/min 后降斜力开始波动但还有一定降斜能力；转速到达160 r/min 后基本失去降斜能力。

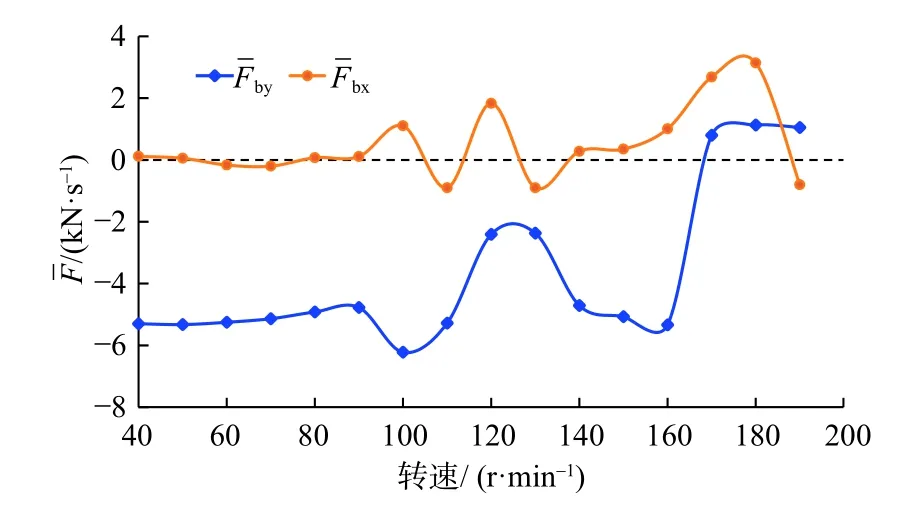
图7 不同转速下平均动态侧向力在x、y 方向分力的变化曲线Fig.7 Variation curve of average dynamic lateral force component in X and Y directions at different speeds

图8 和图9 为3 个阶段间变化趋势明显的90 r/min和160 r/min 附近的涡动轨迹和动态侧向力分布。从图8 和图9 可看出，转速低于90 r/min 时，涡动轨迹和动态侧向力明显集中偏向下井壁分布，动态侧向力在y方向分力稳定表现为降斜力，随转速增大，动态侧向力更加集中且向下井壁冲击次数增多；当转速大于90 r/min 时，涡动轨迹和动态侧向力不再全部集中于下井壁，降斜力产生明显波动，并产生波动的方位变化力，此时平均动态侧向力仍表现为降斜力，但不再稳定；转速在140～160 r/min 时，虽然动态侧向力在井壁四周均有分布，但平均动态侧向力仍表现为较大降斜力；转速大于160 r/min 时，涡动轨迹和动态侧向力不再有偏向下井壁的趋势，此时的降斜力几乎为0，甚至波动为增斜力。

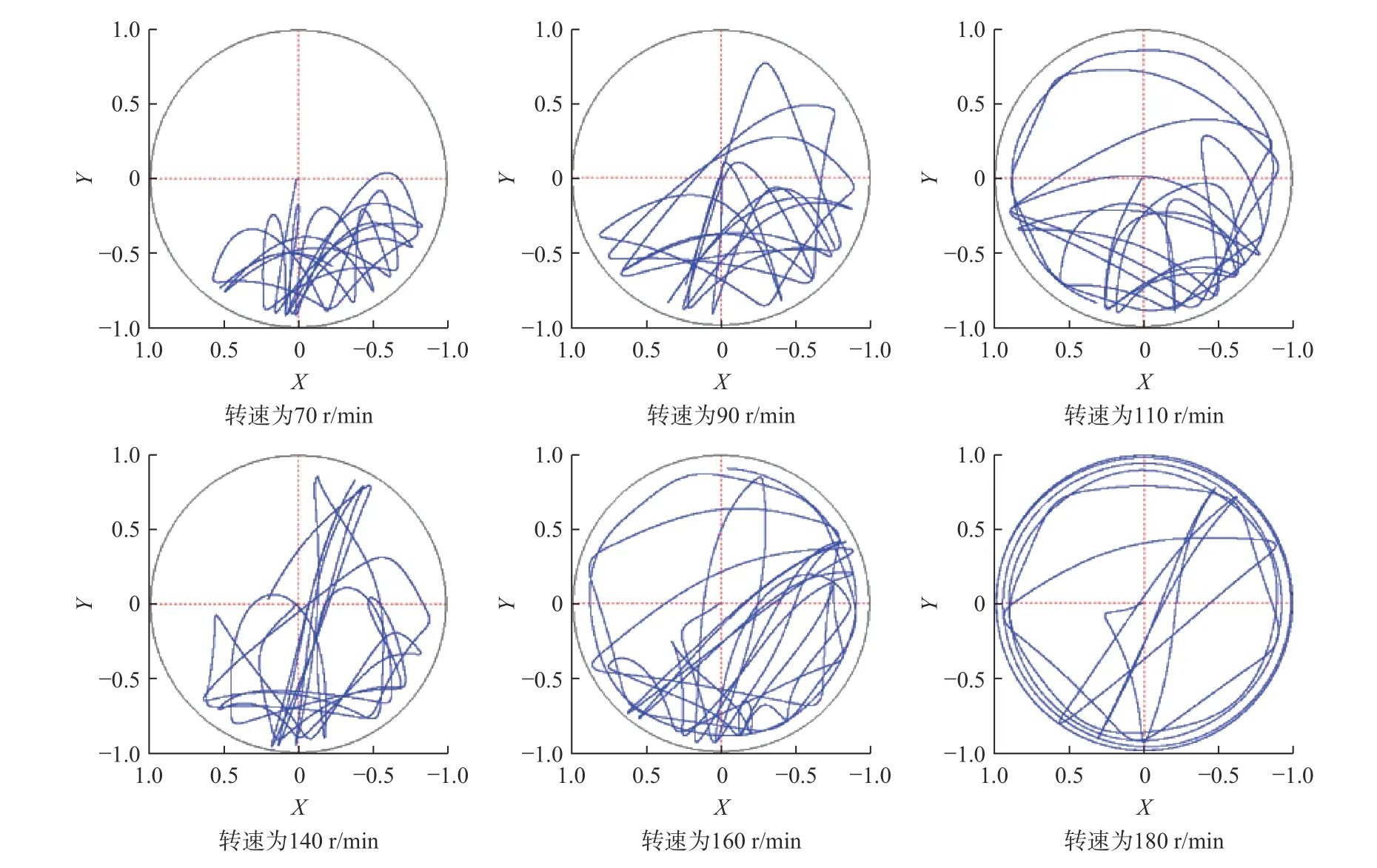
图8 临界转速附近的钻铤形心涡动轨迹图Fig.8 The whirl trajectory of the geometric section center of a drill collar under key rotary speed

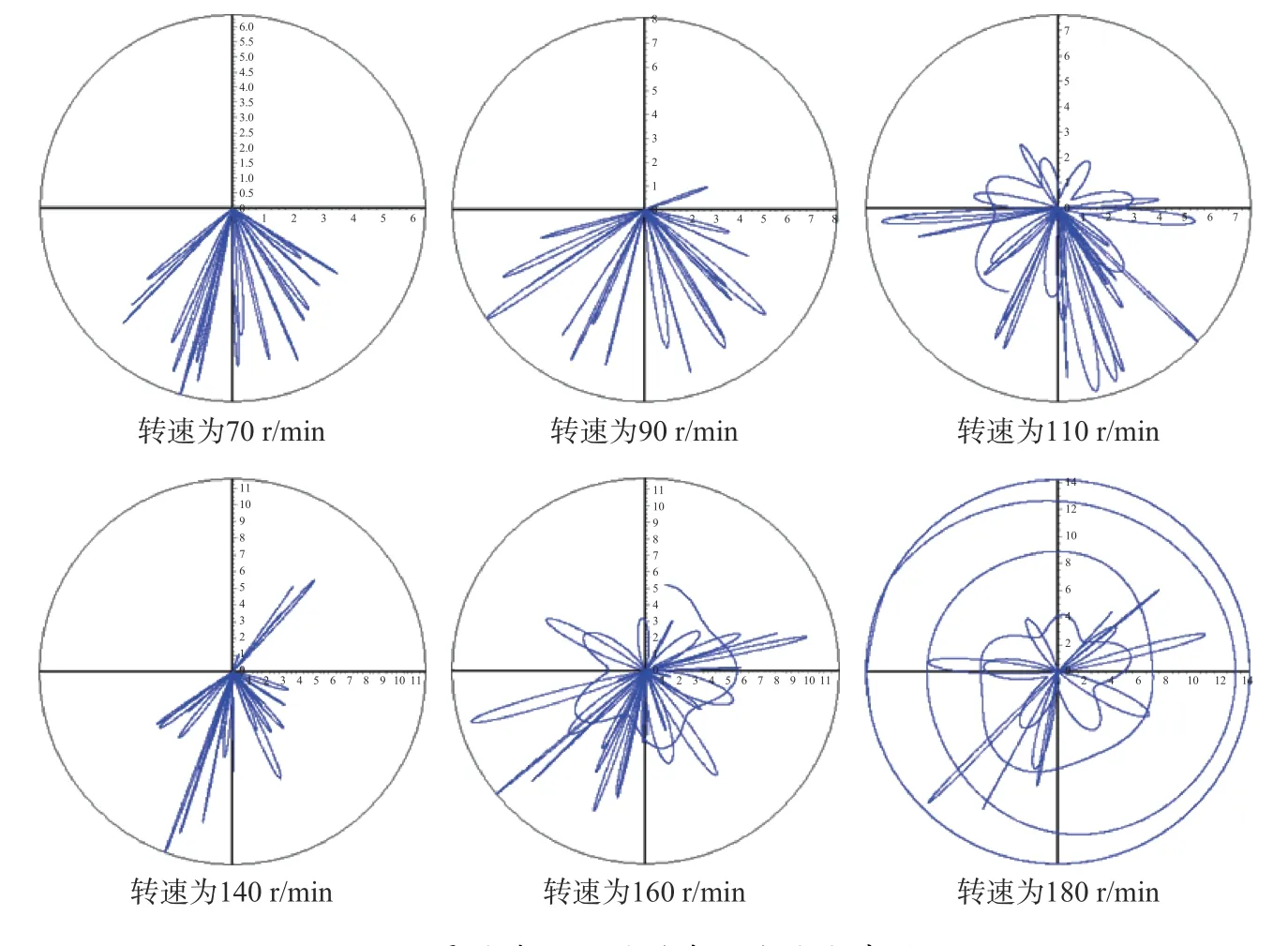
图9 临界转速附近的动态侧向力分布时程图Fig.9 Time-history chart of dynamic lateral force distribution under key rotary speed

结合图7 和图9，可将动态侧向力在y方向分力开始波动且不再明显集中于下井壁时的转速称为第一临界转速，不超过该转速时为稳定降斜阶段，预弯曲钻具组合能够提供很稳定的降斜力；将动态侧向力在y方向分力开始明显不表现为降斜力、x方向也产生较大分力时的转速称为第二临界转速，在第一、第二临界转速间为不稳定降斜阶段，预弯曲钻具组合还能够提供降斜力，但降斜能力不稳定，当转速超过第二临界转速时为丧失降斜能力阶段。

2.3 井斜角对不同转速下防斜性能的影响

为了探究不同井斜角下动态侧向力随井斜角的变化规律的变化，又分别对1°到5°间共4 组井斜角情况下不同转速下的动态侧向力进行计算并绘制曲线，转速计算点间隔为10 r/min，最终发现动态侧向力变化趋势与3°时相似，均可以划分为三个阶段，图10 为第一、第二临界转速随井斜角的变化。

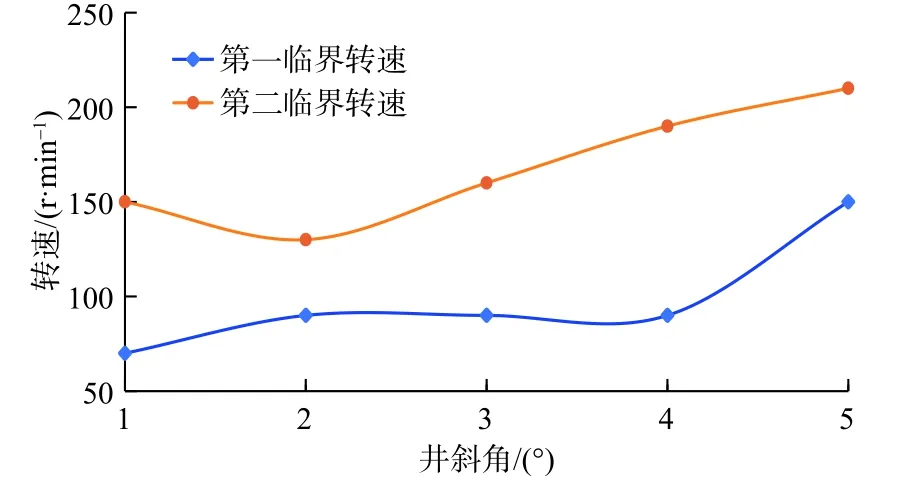
图10 第一、第二临界转速随井斜角的变化曲线Fig.10 Curve of the first and second critical speed with well deviation angle

从图10 及图6 可看出，随井斜角增大，不仅降斜力增大，而且稳定降斜的转速范围也在增大，丧失降斜能力的临界转速也有明显上升趋势，这说明预弯曲钻具组合的降斜能力及稳定性将会随井斜角增大而增大。

仿真结果可为双稳定器预弯曲钻具组合的钻速选择提供理论指导，由不同井斜角下动态侧向力随转速的变化规律可知，双稳定器预弯曲钻具组合在使用时应根据井斜角判断转速的临界值。转速的临界值随井斜角增大而降低，控制转速实现稳定降斜对双稳定器预弯曲钻具组合的使用具有重要意义。

3 结论

(1)将前人建立的动力学模型应用到双稳定预弯曲钻具组合的动力学模拟中，并根据动力学模拟出的涡动轨迹数据建立动态侧向力模型，最终通过钻铤形心涡动轨迹图、动态侧向力分布时程图及平均动态侧向力可以快速且直观的对双稳定器预弯曲钻具组合的降斜特性进行综合评价。

(2)本文所述双稳定器预弯曲钻具组合及相关参数下，平均动态侧向力表现为降斜力，且随井斜角增大而增大；随转速变化，平均动态侧向力可分为稳定降斜、不稳定降斜及丧失降斜能力3 个阶段，且第一、第二临界转速随井斜角的增大而增大。

(3)双稳定器预弯曲钻具组合在井斜角增大时，表现为降斜能力和稳定性的共同提升，充分揭示了预弯曲钻具组合在现场应用的优势，对双稳定器预弯曲钻具组合在现场的应用具有重要意义。

(4)本研究对预弯曲钻具组合动态侧向力的定量评价方法比较直观，但所使用的动力学模型未充分考虑预弯曲结构，需要进一步完善。