带可变径稳定器底部钻具组合的等效刚度及其导向能力分析
2020-06-04王光磊狄勤丰张进双王文昌胡群爱牛新民张金成
王光磊, 狄勤丰, 张进双, 王文昌, 胡群爱, 牛新民, 张金成
(1中国石油化工股份有限公司石油工程技术研究院 2上海大学力学与工程科学学院上海市应用数学和力学研究所)
底部钻具组合(以下简称:BHA)主要由钻头、稳定器及钻铤构成,是钻井作业中的关键工具,其决定着井眼轨迹控制效果,相关的研究工作已有许多[1-14]。但是一直以来,对于带可变径稳定器BHA可形成的不同结构BHA的等效刚度和导向能力这两者之间的关系并未有过论述。等效刚度直接反映BHA的抗弯曲能力,明确其与带可变径稳定器BHA的导向能力之间的关系,对带可变径稳定器BHA在复杂结构井中的应用具有重要指导意义。
带可变径稳定器BHA的关键特征为其稳定器尺寸可以有不同的组合形式,从而达到不同的功能。本文考虑弯曲井眼中不同尺寸稳定器的支座效应,以及钻压及井眼曲率的影响,首先完善BHA纵横弯曲梁三弯矩理论,结合虚功原理,计算BHA的挠曲线方程和应变能,建立带可变径稳定器BHA的等效刚度模型。在此基础上,基于弯曲井眼中的欧拉梁模型[15-16],计算带可变径稳定器BHA的不同导向力特征,探讨带可变径稳定器BHA的形变特征、等效刚度与其导向能力之间的关系。
一、带可变径稳定器BHA的等效刚度
在实际井眼中,由于钻头及稳定器尺寸显著大于钻铤本体,并可在地面顶驱或转盘驱动下转动,因此,可以将钻头及稳定器作为铰支点。为了建模和分析方便,作以下假设:
(1)轴向力及弯曲刚度对于由稳定器分隔的各钻铤跨度各不相同,但在各跨度内设为常数。
(2)忽略BHA径向变形引起的轴向缩短。
(3)由稳定器分隔的左右两部分钻铤在节点处位移连续,转角连续。
1. 带可变径稳定器BHA的连续弯矩方程
受钻压、重力作用及井眼轨迹约束,带可变径稳定器BHA产生变形,在节点位置受等效弯矩作用,如图1所示。

图1 带可变径稳定器的BHA及其受力示意图
建立如图1所示坐标系,其中x轴为水平向右,y轴垂直向上。由于在弯曲井眼中变径稳定器处存在径向位移落差,因此,相应节点上产生附加转角αi为[17]:
(1)
式中:li—各段长度,m;hi—各支座高度,m。
同时考虑到重力、井眼初始弯曲以及钻压在i节点处产生的转角满足连续性要求,基于连续弯曲梁理论,可推导得到关于节点的弯矩方程为:
(2)

式中:qi—重力在横向的均布分量,N/m;
Mi—节点的等效弯矩,N·m;
Pi—节点轴向载荷,N;
E—弹性模量,N/m2;
Ii—惯性矩,m4。
受井眼轨迹约束,钻头及距钻头最远的稳定器处弯矩为:
(3)
式中:k1,kn—分别为第一段和最后一段的井眼曲率;
n—稳定器个数,也即BHA被稳定器分割的段数。
根据式(2),并结合边界条件式(3),即可计算出每个稳定器处的弯矩。
AM=Θ
(4)
式中:A—系数矩阵。
(5)
当i≥2时
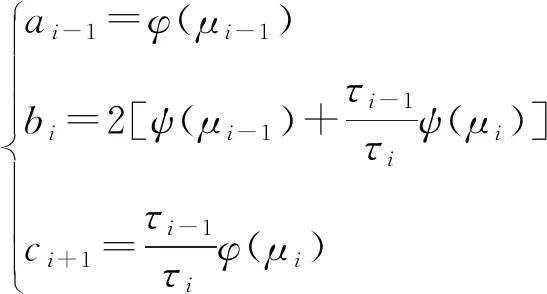
(6)
M为弯矩矩阵:
(7)
外部因素引起的转角相关项矩阵Θ为:
(8)
其中:
社区消费者之间的互动包括线上和线下两方面。依托地域优势,居民在社区中经常面对面交流,分享消费体验,实现口碑传播。线上传播则更为便捷:一是基于平台上对产品的在线评论,为社区其他消费者的购买决策提供依据;二是借助微信、微博等社交媒体进行交流和互动,分享自己的消费经历、推荐产品等。消费者间的相互分享降低了彼此选择成本,价值得到增加。
(9)
利用高斯消去法、追赶法等可以对矩阵方程(4)进行求解,得到所有节点上的弯矩值。
2. 带可变径稳定器BHA的等效刚度
考虑每一跨梁上节点弯矩、轴向力、分布重力的作用,产生的弯曲变形可由各项叠加而得:
(10)
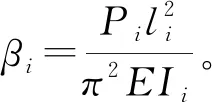
各段最大挠度必须满足井壁限制条件:
(11)
式中:Dw—井眼直径;
Doi—第i段钻具外径。
当式(11)不满足时,表明钻具与井壁发生接触,此时在接触位置设一铰接点,重新划分分段,按式(4)计算弯矩,并利用式(10)重新计算各段的弯曲变形,直到式(11)成立。
(12)
因此,带可变径稳定器BHA的弯曲应变能为:
(13)
定义带可变径稳定器BHA的弯曲应变能与相应的光钻铤BHA弯曲应变能U0的比值为:
(14)

λ—BHA的抗弯能力。
稳定器越多,钻铤外径越大,λ越大,所用BHA的刚度就越大。定义井眼曲率为5°/30 m时的λ为BHA的等效刚度系数。
(15)
则BHA的等效刚度可表示为:
(EI)eq=λEI(EI)o
(16)
式中:(EI)o—光钻铤的刚度,Nm2。
当光钻铤外径给定时,(EI)o给定。因此,等效刚度系数就能反映等效刚度的变化规律。后文中,用等效刚度系数来反映带可变径稳定器BHA的等效刚度特征。
二、带可变径稳定器BHA的导向力
受三维弯曲井眼井壁约束的BHA在重力、浮力、轴向力和弯矩的联合作用下,将在钻头处形成侧向作用力。基于小变形假设、平衡方程,根据文献[2]利用加权余量法可求得钻头的井斜力Fα和方位力Fφ。钻头的合作用效果可以利用旋转一周内钻头上的合导向力来表述。
(17)
式中:Fα、Fφ—BHA在某一装置角时钻头上的造斜力和方位力,N;
s—计算点数,即将钻头旋转1周均匀分割为s等份。
三、实例及参数影响分析
取常用的双稳定器组合:Ø311.2 mm钻头+Ø228.6 mm钻铤×1.2 m+近钻头可变径稳定器+Ø228.6 mm钻铤×18 m+上可变径稳定器+203.2 mm钻铤…。
可变径稳定器外径调节范围为292~311 mm。在此区间内计算BHA的等效刚度系数及其导向力。钻压160 kN;钻井液密度1.80 g/cm3,钻头处井斜角为30°。可变径稳定器的等效刚度系数随稳定器外径的变化关系如图2所示。
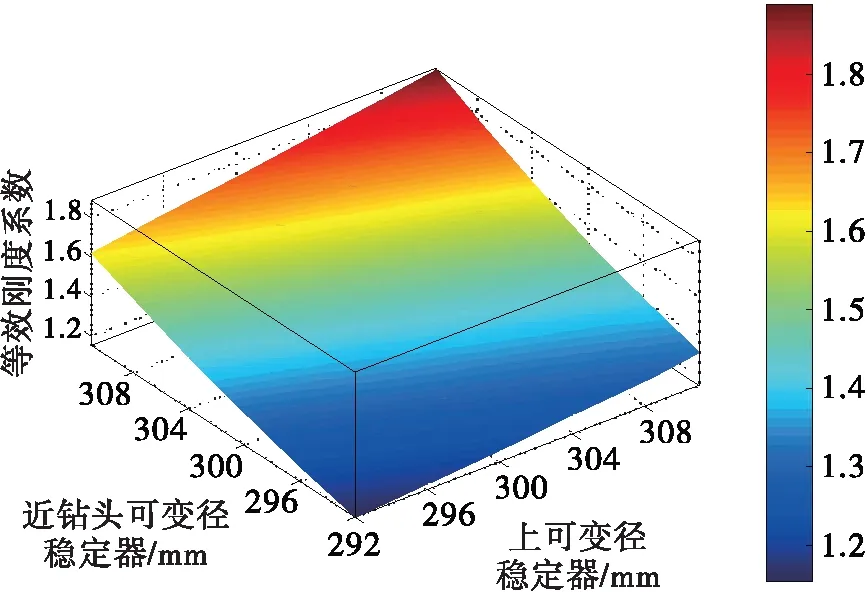
图2 不同稳定器外径组合时BHA的等效刚度系数
从图2中可以看出,带可变径稳定器BHA的等效刚度系数随稳定器外径的变化而变化。当两个稳定器均达到最大尺寸时,其等效刚度系数最大,反映出其抵抗弯曲变形的能力越强。近钻头稳定器尺寸较大,而上部稳定器外径在区间内变化时,其整体等效刚度系数相对较大;当上可变径稳定器外径较大,近钻头稳定器外径变化对等效刚度系数梯度影响较大。当两个稳定器均处于较小外径时,其等效刚度系数最小,即在井眼内最容易发生变形。由于等效刚度系数最低时,BHA最容易变形,因此,当BHA下入困难时,可以选择具有较小等效刚度系数的BHA结构实现钻柱的下入。之后,可以通过调整可变径稳定器外径达到不同的井眼控斜目的,如图3所示。
从图3中可以看出,当上稳定器外径为292 mm,近钻头稳定器外径由311 mm变化到292 mm时,BHA由增斜变为降斜;当上稳定器外径为292 mm,近钻头稳定器外径为311 mm时,增斜力最大。类似的,当上稳定器外径为311 mm,近钻头稳定器外径由311 mm变化到292 mm时,BHA由增斜变为降斜;当上稳定器外径为311 mm,近钻头稳定器外径为292 mm时,降斜效果最强。
带可变径稳定器BHA的等效刚度系数反映出BHA在弯曲井眼中抗变形的能力,结合其导向能力分析,可以为更准确地把握实际复杂结构井对井身质量的要求,能够从新的角度提供一种带可变径稳定器BHA的应用方案。
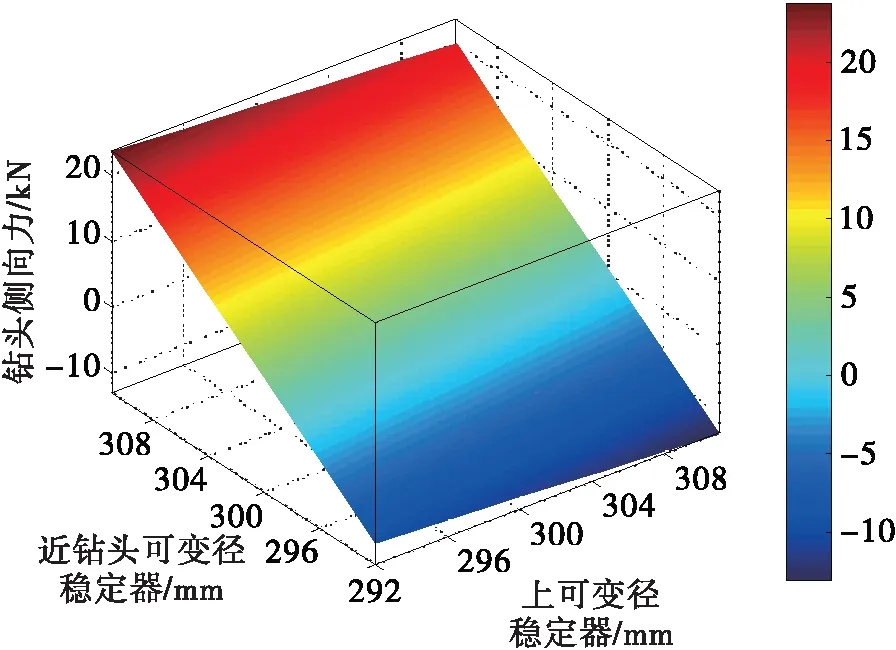
图3 不同稳定器外径组合时BHA的钻头侧向力
四、结论
(1)结合虚功原理及考虑支座沉降的纵横弯曲梁理论,提出的带可变径稳定器BHA的等效刚度系数可以有效指导BHA在复杂结构井眼轨迹控制中的应用。
(2)对于带可变径稳定器BHA,一般而言,稳定器外径越大,其抗弯曲能力越强,等效刚度系数越大,反之亦然。近钻头稳定器直径变化对BHA的等效刚度系数和钻头侧向力影响较大。
(3)对于具有降斜效果的不同钻具组合结构,等效刚度系数越大,降斜力越大;而对于具有增斜效果的不同钻具组合结构,等效刚度系数越大,增斜力越小。
(4)通过调整近钻头或上部稳定器外径,均可实现BHA功能(增斜或降斜)的改变。综合考虑带可变径稳定器的等效刚度系数及其侧向力,可以为油田现场提供更优的带可变径稳定器BHA使用方案。
